Similar presentations:
Дистрибутивная рекурсия
1.
ДИСТРИБУТИВНАЯ РЕКУРСИЯ2. Дистрибутивная рекурсия
Механизм, посредством которого свойства потокасмешения непрерывно обновляются в процессе
оптимизации для достижения установленной точности
расчета
Абсолютная погрешность
(Pc - Pp)
Относительная погрешность
(Pc - Pp)/Pp
– Pc = текущее значение свойства
– Pp = значение свойства на предыдущем шаге
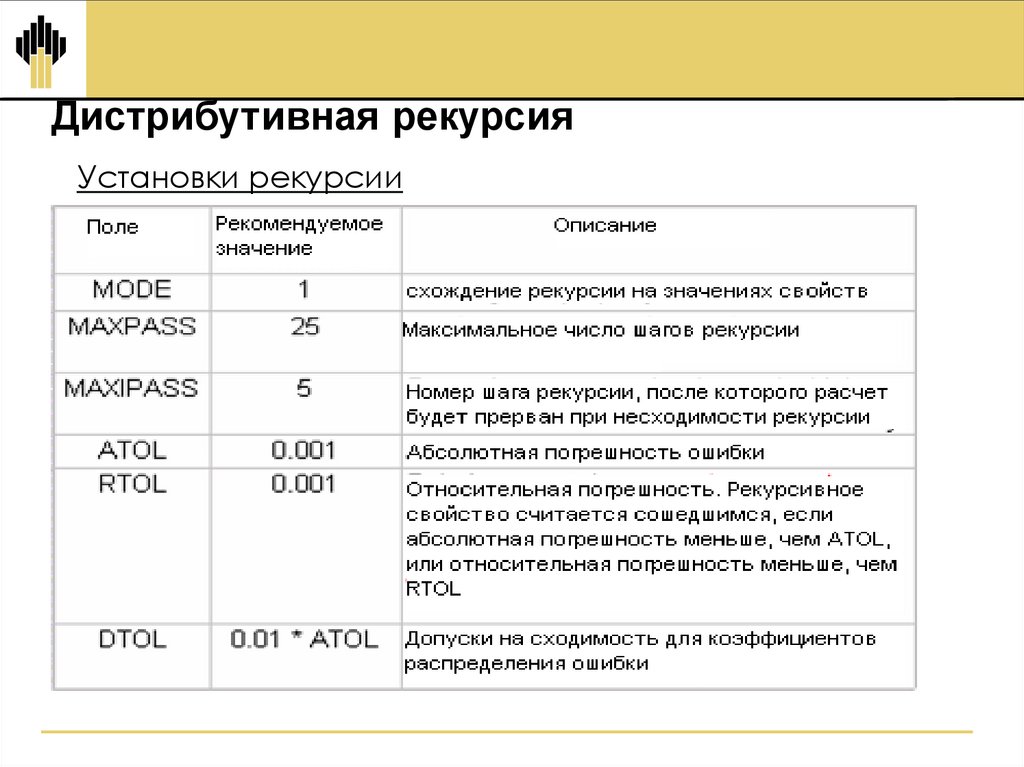
Настройки рекурсии
– Maxpass =n
– ATOL и RTOL
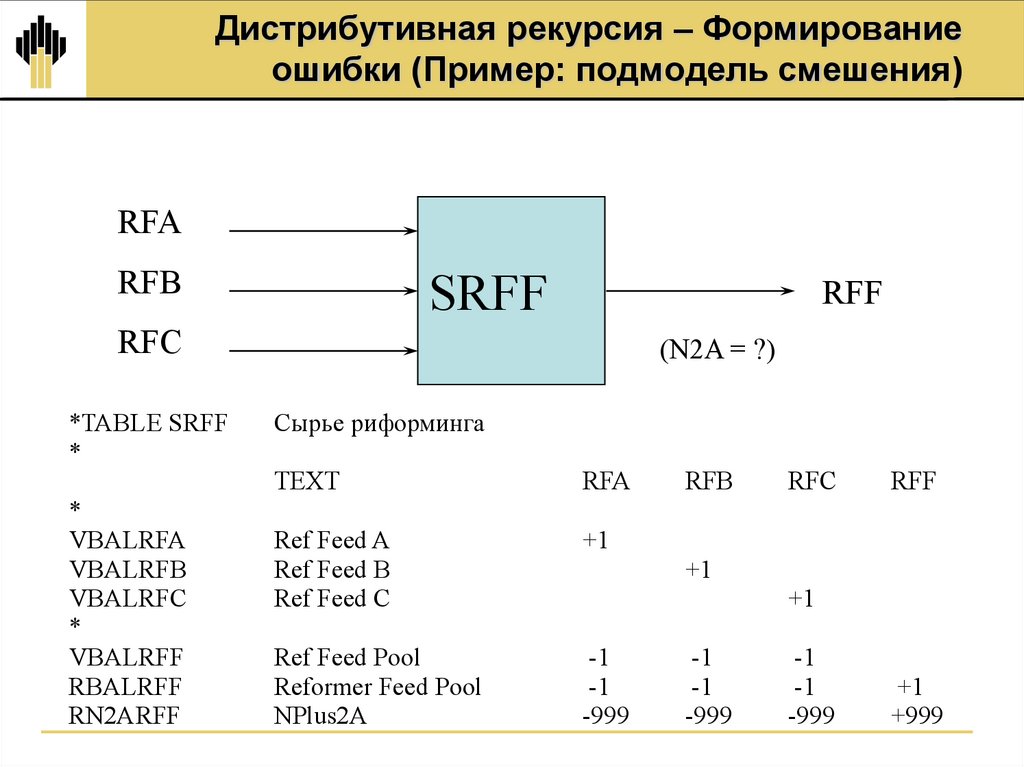
3. Дистрибутивная рекурсия – Формирование ошибки (Пример: подмодель смешения)
RFARFB
SRFF
RFF
RFC
*TABLE SRFF
*
*
VBALRFA
VBALRFB
VBALRFC
*
VBALRFF
RBALRFF
RN2ARFF
(N2A = ?)
Сырье риформинга
TEXT
RFA
Ref Feed A
Ref Feed B
Ref Feed C
+1
Ref Feed Pool
Reformer Feed Pool
NPlus2A
-1
-1
-999
RFB
RFC
RFF
+1
+1
-1
-1
-999
-1
-1
-999
+1
+999
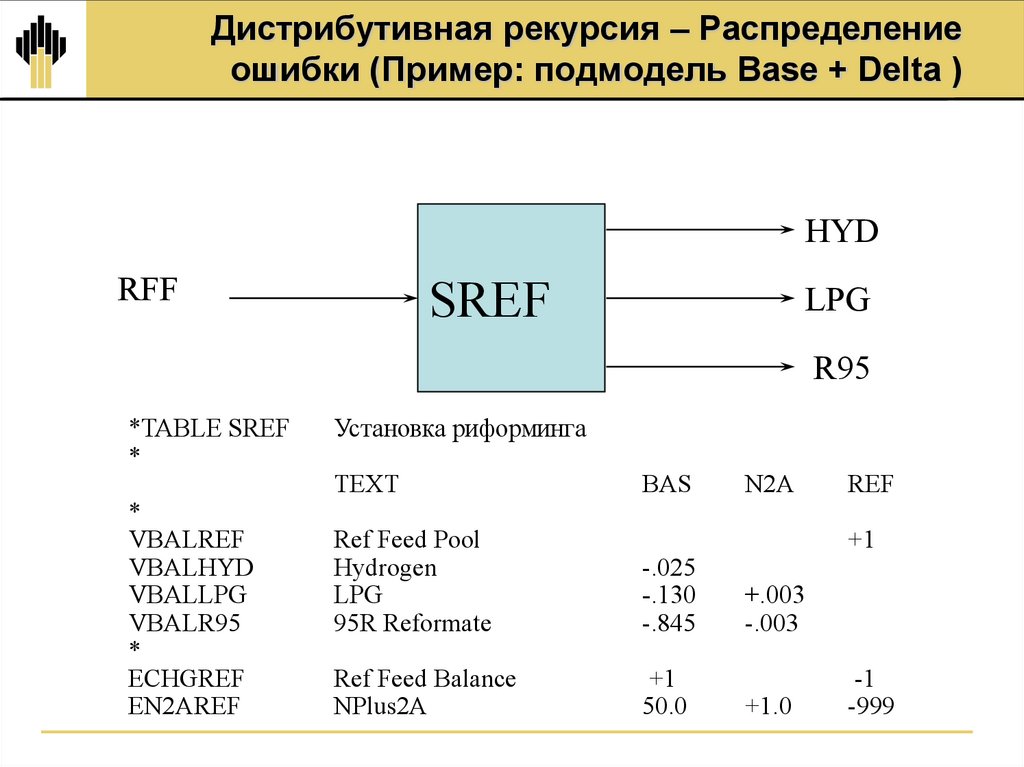
4. Дистрибутивная рекурсия – Распределение ошибки (Пример: подмодель Base + Delta )
HYDRFF
SREF
LPG
R95
*TABLE SREF
*
*
VBALREF
VBALHYD
VBALLPG
VBALR95
*
ECHGREF
EN2AREF
Установка риформинга
TEXT
BAS
Ref Feed Pool
Hydrogen
LPG
95R Reformate
-.025
-.130
-.845
Ref Feed Balance
NPlus2A
+1
50.0
N2A
REF
+1
+.003
-.003
+1.0
-1
-999
5.
Дистрибутивная рекурсияPIMS Таблицы дистрибутивной рекурсии
PGUESS
Определяет, какие свойства, для каких потоков должны
рассчитываться рекурсивно и обеспечивает начальные оценки
значений свойств. Имена столбцов – трехсимвольные коды
свойств. Имена строк в таблице – трехсимвольные коды потоков.
PDIST
Для каждого потока, перечисленного в строках таблицы PGUESS,
ожидаемое распределение ошибки в назначения могут быть
указаны в таблице PDIST. Название столбцов таблицы –
трехсимвольные коды рекурсивных потоков. Именами строк
являются трехсимвольные коды потоков назначения, в которые
распределяется ошибка.
PCALC
Хотя эта таблица не находится в категории Рекурсия, эта
таблица используется для пересчета свойства одного потока из
другого с помощью коэффициента. (Коэффициент m в
уравнении Y=mX+b)
6. Дистрибутивная рекурсия
Правила создания рекурсивных потоков смешения(пулов)
– Коэффициенты для компонентов отрицательные (). Коэффициенты для пула положительные (+)
– Отрицательные коэффициенты для строк WBAL и
RBAL должны совпадать, иначе возможны
проблемы с распределением ошибки
– Не допускаются любые коэффициенты для пула в
строке WBAL, в противном случае вероятно
несходимое решение
– 3-х символьное имя столбца пула должно
совпадать с кодом существующего
материального потока модели
7. Имена строк, в которых происходит формирование и распределение ошибки
Формирование ошибки– Rquafff
Распределение ошибки
1. В подмодель
2. В смесь по спецификации
3. В другой пул
• Где:
fff
qua
Equadst (L,G)
Nquaprd, Xquaprd
Rquaggg
первичный рекурсивный пул
рекурсивное свойство
dst
назначение
prd
конечный продукт
ggg
вторичный рекурсивный пул
8.
Дистрибутивная рекурсияВыполнение ДР в модели
Составление комбинаций строк RBALstr и Rprpstr
Все строки R - равенства
Все рекурсивные потоки “str” должны существовать
RBALstr строка должна содержать +1 в столбце
рекурсивного пула “str”
Все рекурсивные свойства для потока “str” должны
иметь начальные оценочные значения в строке “str” в
таблице PGUESS
9.
ОпределениеРекурсия – процесс решения модели, включающий в
себя:
Исследование оптимального решения с использованием
внешней программы;
Расчет данных физических качеств;
Обновление модели с учетом расчетных данных;
Повторное решение модели;
Процесс повторяется до достижения
данными указанных допусков.
расчетными
10.
История (1)В начале эпохи линейного программирования при построении
модели такого процесса как нефтепереработка для части данных в
модели приходилось принимать оценочные значения.
В качестве этих данных обычно выступали данные физических
качеств материалов, используемых при переработке нефти для
производства целевых нефтепродуктов.
К примеру, при смешении бензина должно обеспечиваться
соответствие определенным требованиям по октановому числу,
давлению паров, содержанию серы, фракционному составу и прочим
параметрам качеств.
При вводе данных для каждого из компонентов смеси,
используемых оптимизатором для смешения бензина, пользователю
приходилось использовать оценочные значения для большинства из этих
параметров.
11.
История (2)Поскольку
существенная
часть
этих
данных
представляла
собой
пользовательские предположения, данные в модели бывали неточными или
неверными.
Для компенсации был разработан способ улучшения данных в ходе решения
модели: оптимизатор сначала решал модель, содержащую оценочные данные,
после решения модели внешняя компьютерная программа, написанная на языке
программирования типа Fortran, PL/1 или на ассемблере, рассчитывала данные
физических свойств, использованные в модели, из оптимального решения. Другими
словами, внешняя программа исследовала оптимальное решение, только что
созданное оптимизатором, и рассчитывала данные физических качеств нефтяных
фракций на основании состава нефтяного сырья в решении.
Эти данные затем вставлялись в модель (в матрицу ЛП). Таким образом,
оценочные данные заменялись более точными данными. Модель повторно
передавалась оптимизатору и решалась снова. Та же самая внешняя программа
затем исследовала новое решение, те же данные повторно рассчитывались,
повторно вставлялись в матрицу, и модель решалась снова.
Этот процесс повторялся, пока изменения в рассчитанных данных не
становились достаточно малыми для удовлетворения определенных допусков,
указанных во внешней программе.
12.
Принцип дистрибутивной рекурсии (1)После решения текущей матрицы с использованием
начальных оценок или предположений в отношении
физических качеств на основе этого решения вычисляются
новые значения, которые вводятся в матрицу для
следующего решения ЛП.
Главное отличие между
дистрибутивной и простой рекурсией состоит в способе
обработки
разницы
между
предположенными
и
рассчитанными из решения данными физических
качеств.
Эта
разница
называется
"ошибкой".
Когда
пользователь высказывает предположения относительно
физических свойств рекурсивных пулов в модели ЛП,
вносится ошибка, поскольку предположения пользователя
всегда неверны.
13.
Принцип дистрибутивной рекурсии (2)Дистрибутивная рекурсия называется «дистрибутивной»,
поскольку происходит распределение - дистрибуция - этой
ошибки по всем местам использования данного качества.
Зависимые места, в которых используются физические свойства
рекурсивного пула, следовательно, можно отследить в
обратном направлении до самого источника пула.
Структура
матрицы
дистрибутивной
рекурсии
предоставляет возможность отслеживания ("видимость") от
источника рекурсивного пула до пункта его распределения и в
обратном направлении.
14.
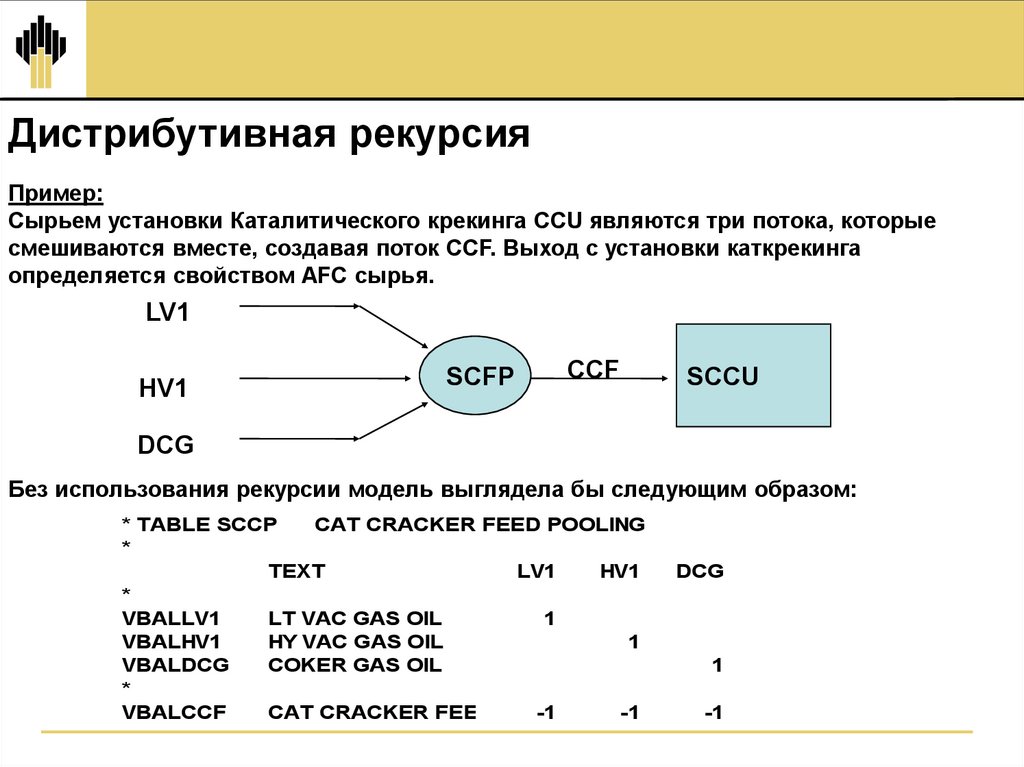
Дистрибутивная рекурсияПример:
Сырьем установки Каталитического крекинга CCU являются три потока, которые
смешиваются вместе, создавая поток CCF. Выход с установки каткрекинга
определяется свойством AFC сырья.
LV1
HV1
SCFP
CCF
SCCU
DCG
Без использования рекурсии модель выглядела бы следующим образом:
* TABLE SCCP
CAT CRACKER FEED POOLING
*
TEXT
LV1
HV1
*
VBALLV1
LT VAC GAS OIL
1
VBALHV1
HY VAC GAS OIL
1
VBALDCG
COKER GAS OIL
*
VBALCCF
CAT CRACKER FEED
-1
-1
DCG
1
-1
15.
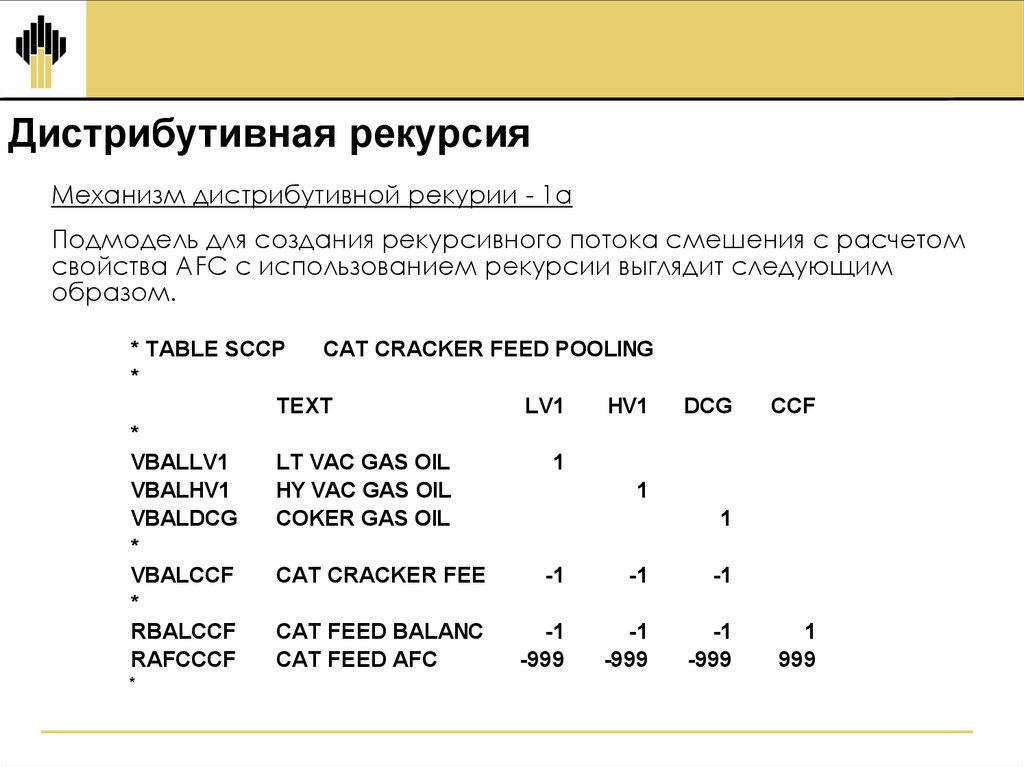
Дистрибутивная рекурсияМеханизм дистрибутивной рекурии - 1a
Подмодель для создания рекурсивного потока смешения с расчетом
свойства AFC с использованием рекурсии выглядит следующим
образом.
* TABLE SCCP
CAT CRACKER FEED POOLING
*
TEXT
LV1
HV1
*
VBALLV1
LT VAC GAS OIL
1
VBALHV1
HY VAC GAS OIL
1
VBALDCG
COKER GAS OIL
*
VBALCCF
CAT CRACKER FEED
-1
-1
*
RBALCCF
CAT FEED BALANCE
-1
-1
RAFCCCF
CAT FEED AFC
-999
-999
*
DCG
CCF
1
-1
-1
-999
1
999
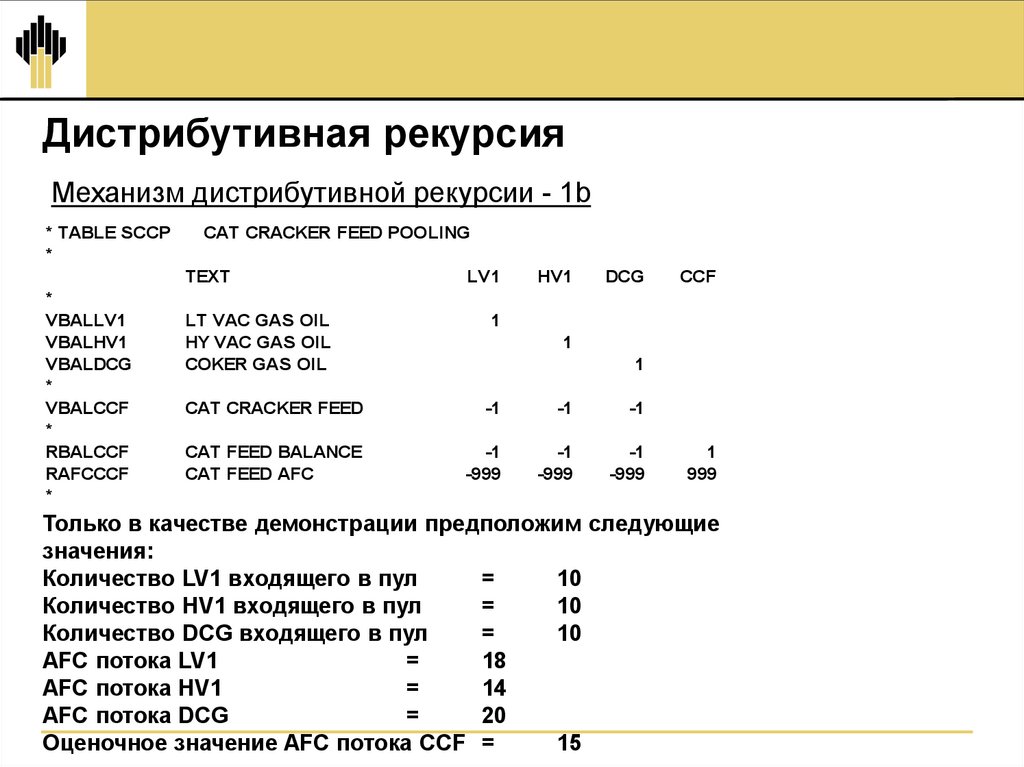
16.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 1b
* TABLE SCCP
*
CAT CRACKER FEED POOLING
TEXT
*
VBALLV1
VBALHV1
VBALDCG
*
VBALCCF
*
RBALCCF
RAFCCCF
*
LV1
HV1
DCG
LT VAC GAS OIL
HY VAC GAS OIL
COKER GAS OIL
1
CAT CRACKER FEED
-1
-1
-1
CAT FEED BALANCE
CAT FEED AFC
-1
-999
-1
-999
-1
-999
CCF
1
1
1
999
Только в качестве демонстрации предположим следующие
значения:
Количество LV1 входящего в пул
=
10
Количество HV1 входящего в пул
=
10
Количество DCG входящего в пул
=
10
AFC потока LV1
=
18
AFC потока HV1
=
14
AFC потока DCG
=
20
Оценочное значение AFC потока CCF =
15
17.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 2a
Значения AFC для LV1, HV1 и DCG будут доступны из любого места модели;
начальное оценочное значение AFC для CCF берется из таблицы PGUESS
Исходя из строки RBAL, которая является равенством, активность столбца CCF = 30
После умножения в строке RAFCCCF, которая также является равенством, получили
равенство 450 - 520 = 0, что неверно. Однако, PIMS также создает столбец,
RAFCCCF (вектор ошибки), помещающий 1 в строку RAFCCCF, и активность этого
вектора принимает такое значение, что равенство становится верным. Этот
столбец, созданный PIMS можно увидеть в Matrix Listing Report.
* TABLE SCCP
*
CAT CRACKER FEED POOLING
TEXT
*
VBALLV1
VBALHV1
VBALDCG
*
VBALCCF
*
RBALCCF
RAFCCCF
*
10
LV1
10
HV1
10
DCG
LT VAC GAS OIL
HY VAC GAS OIL
COKER GAS OIL
1
CAT CRACKER FEED
-1
-1
-1
CAT FEED BALANCE
CAT FEED AFC
-1
-18
-1
-14
-1
-20
30
CCF
RAFCCF
1
15
+1
1
1
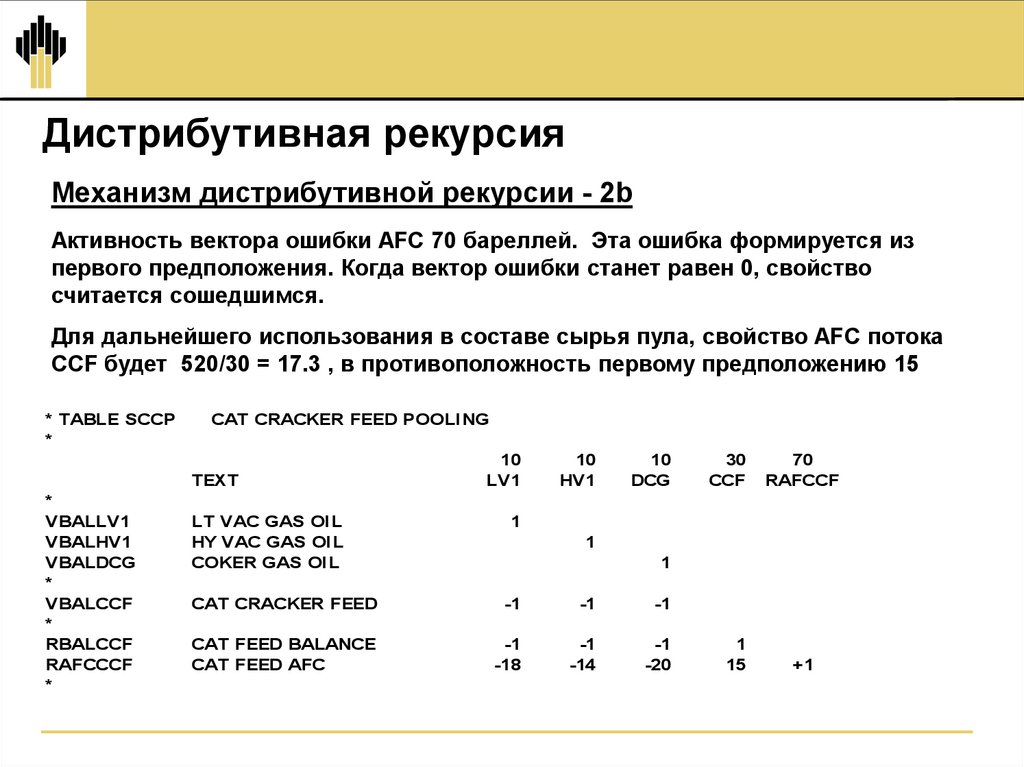
18.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 2b
Активность вектора ошибки AFC 70 бареллей. Эта ошибка формируется из
первого предположения. Когда вектор ошибки станет равен 0, свойство
считается сошедшимся.
Для дальнейшего использования в составе сырья пула, свойство AFC потока
CCF будет 520/30 = 17.3 , в противоположность первому предположению 15
* TABLE SCCP
*
CAT CRACKER FEED POOLING
TEXT
*
VBALLV1
VBALHV1
VBALDCG
*
VBALCCF
*
RBALCCF
RAFCCCF
*
10
LV1
10
HV1
10
DCG
LT VAC GAS OIL
HY VAC GAS OIL
COKER GAS OIL
1
CAT CRACKER FEED
-1
-1
-1
CAT FEED BALANCE
CAT FEED AFC
-1
-18
-1
-14
-1
-20
30
CCF
70
RAFCCF
1
15
+1
1
1
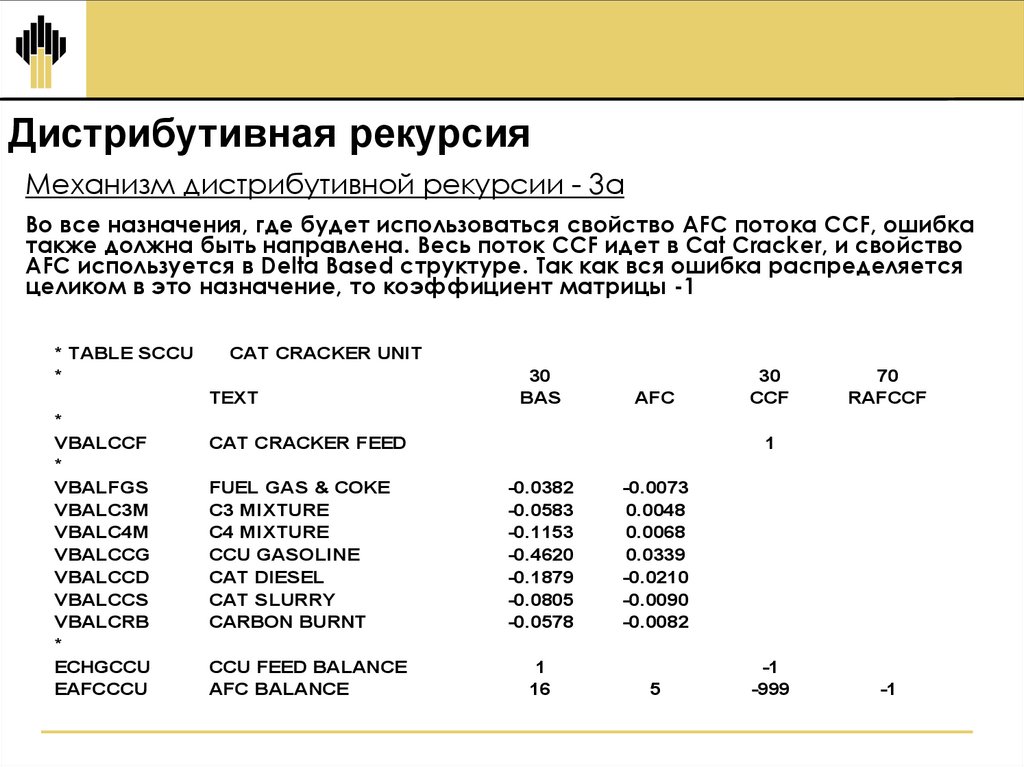
19.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 3a
Во все назначения, где будет использоваться свойство AFC потока CCF, ошибка
также должна быть направлена. Весь поток CCF идет в Cat Cracker, и свойство
AFC используется в Delta Based структуре. Так как вся ошибка распределяется
целиком в это назначение, то коэффициент матрицы -1
* TABLE SCCU
*
CAT CRACKER UNIT
TEXT
*
VBALCCF
*
VBALFGS
VBALC3M
VBALC4M
VBALCCG
VBALCCD
VBALCCS
VBALCRB
*
ECHGCCU
EAFCCCU
30
BAS
AFC
CAT CRACKER FEED
30
CCF
70
RAFCCF
1
FUEL GAS & COKE
C3 MIXTURE
C4 MIXTURE
CCU GASOLINE
CAT DIESEL
CAT SLURRY
CARBON BURNT
-0.0382
-0.0583
-0.1153
-0.4620
-0.1879
-0.0805
-0.0578
CCU FEED BALANCE
AFC BALANCE
1
16
-0.0073
0.0048
0.0068
0.0339
-0.0210
-0.0090
-0.0082
5
-1
-999
-1
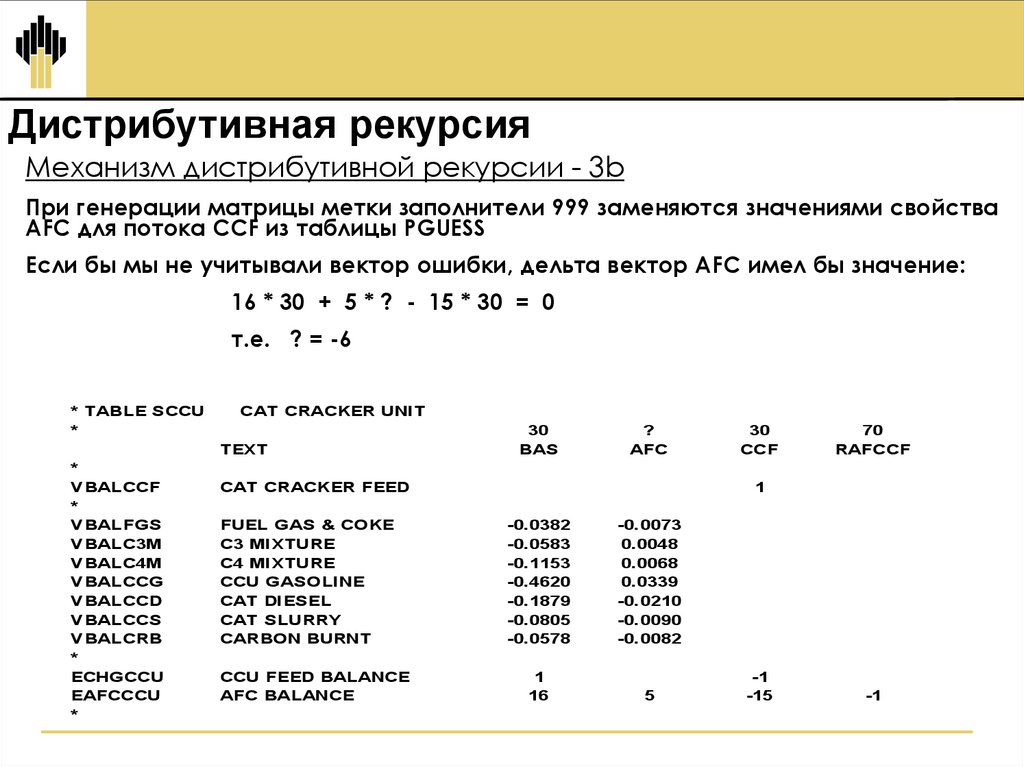
20.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 3b
При генерации матрицы метки заполнители 999 заменяются значениями свойства
AFC для потока CCF из таблицы PGUESS
Если бы мы не учитывали вектор ошибки, дельта вектор AFC имел бы значение:
16 * 30 + 5 * ? - 15 * 30 = 0
т.е. ? = -6
* TABLE SCCU
*
CAT CRACKER UNIT
TEXT
*
VBALCCF
*
VBALFGS
VBALC3M
VBALC4M
VBALCCG
VBALCCD
VBALCCS
VBALCRB
*
ECHGCCU
EAFCCCU
*
30
BAS
?
AFC
CAT CRACKER FEED
30
CCF
70
RAFCCF
1
FUEL GAS & COKE
C3 MIXTURE
C4 MIXTURE
CCU GASOLINE
CAT DIESEL
CAT SLURRY
CARBON BURNT
-0.0382
-0.0583
-0.1153
-0.4620
-0.1879
-0.0805
-0.0578
CCU FEED BALANCE
AFC BALANCE
1
16
-0.0073
0.0048
0.0068
0.0339
-0.0210
-0.0090
-0.0082
5
-1
-15
-1
21.
Дистрибутивная рекурсияМеханизм дистрибутивной рекурсии - 3c
При активности дельта вектора -6, будет получено больше
бензина CCU и меньше дизеля CCU.
Однако, если вектор ошибки не рассматривать, то дельтавектор имел бы активность :
16 * 30 + 5 * ? - 15 * 30 - 1 * 70 = 0
ie ? = +8
Эффект обратный, который показывает, как изменяются выхода
Каткрекинга при увеличении св-ва AFC.
Если бы начальное предположение свойства AFC для CCF было
правильное, т.е. 17.3, то дельта вектор имел бы активность:
16 * 30 + 5 * ? - 17.3 * 30 - 1 * 0 = 0
ie ? = +8
Хотя мы предположили AFC равным 15, на каткрекинге
используется истинное значение 17.3 благодаря распределению
вектора ошибки RAFCCCF в сроку EAFCCCU.
22.
Дистрибутивная рекурсияРаспределение ошибки
Ошибки распределяются везде, где используется
свойство, т.е. в строках рекурсии, смешения, контрольных
строках
Неправильное или отсутствующее распределение
ошибки может стать причиной локального оптимума
– Коэффициент распределения ошибки =
Объем @ Назначения
Объем @ источника
Коэффициенты распределения ошибки в сумме могут
быть больше 1 при использовании таблицы PCALC
PIMS рассчитывает коэффициенты распределения
ошибки и помещает их в таблицу !PDIST
23.
Дистрибутивная рекурсияВозможные ловушки в рекурсии
Хотя распределение ошибки – это функция, с помощью которой
работает дистрибутивная рекурсия, некорректное моделирование ее
может привести к локальному оптимуму.
Каскадное использование PCALC
Несовпадение рекурсивного и материального баланса
Изменение значения свойства, ограниченного с помощью дэмпингфактора или при помощи Min/Max значения в модели
Чрезмерно ограниченная модель
Выключение и включение установок и смесей, используя таблицу CASE, в
которые распределяется ошибка.
Несходимость при первом шаге рекурсии
Активное распределение ошибки на выключенную установку.
24.
Дистрибутивная рекурсияУстановки рекурсии















 mathematics
mathematics








