Introduction to Segment tree

1. Introduction to Segment tree.

2.

Дерево отрезков — это структура данных, которая позволяет за
асимптотику O(log n) реализовать любые операции, определяемые
на множестве, на котором данная операция ассоциативна, и
существует нейтральный элемент относительно этой операции.
Но стоит заметить, что класс задач, решаемых с помощью дерева
отрезков, намного больше.
Segment tree – is a data structure that allows to implement operations
on the interval in O(log n).
The operation should have an associative property
and have a neutral element

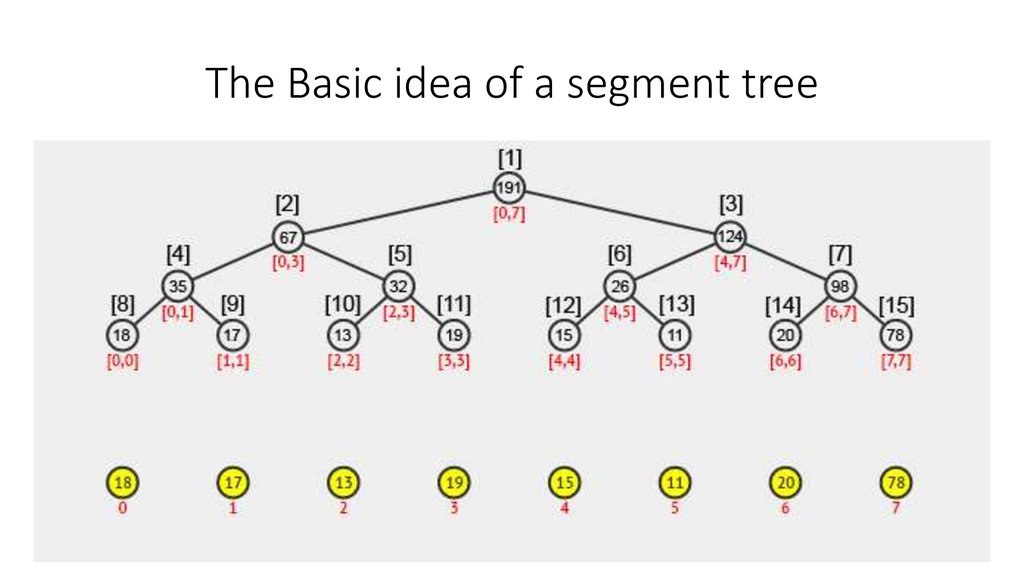
3. The Basic idea of a segment tree

4.

• Рассмотрим пример реализации дерева отрезков для следующих
запросов:
1) Добавить к i-му элементу значение d
2) Получить сумму на отрезке [l;r]
• The Example of queries for the segment tree:
1) To add a value d to the value of i-th element
2) To get sum on the segment [l;r]

5. Creating structure

struct Tree
{
vector<int> t;
int size;
};

6. Initialization of the tree

void init(vector<int> &a){
size = 1;
while(size <= n) size *= 2;
t.resize(2 * size, 0); //0 – neutral element for “+”
for (int i = 0; i < (int)a.size(); i++)
t[i + size] = a[i];
for (int i = size - 1; i > 0; i--)
t[i] = t[2*i]+t[2*i+1];
}

7. The change request

void change(int v, int tl, int tr, int i, int d){
if (tl == tr){
t[v] += d;
return;
}
int mid = (tl + tr) / 2;
if (i <= mid) change(2*v, tl, mid, i, d);
else change(2*v+1, mid + 1, tr, i, d);
t[v] = t[2*v] + t[2*v+1];
}
change(1, 0, size - 1, i, d); //Start

8. Getting sum

int sum(int v, int tl, int tr, int l, int r){
if (l > r) return 0;
if (tl == l && tr == r){
return t[v];
}
int mid = (tl + tr) / 2;
int left_sum = sum(2*v, tl, mid, l, min(r, mid));
int right_sum = sum(2*v+1, mid+1, tr, max(l, mid+1), r);
return left_sum + right_sum;
}
sum(1, 0, size - 1, l, r);

9. Let’s make the task more difficult

Запросы:
1) Изменить значение элементов [l;r] на d
2) Получить сумму на [l;r]
• Для этого нам придётся воспользоваться методом
«запаздывающего обновления».
Requests:
1) Add the value d to every element on the segment [l;r]
2) Get sum on the segment [l;r]
• We use the method of “lazy propagation”

10.

struct Tree
{
vector<int> t;
vector<int> add
int size;
// array for method of “lazy propagation”
void init(vector<int> &a, int n){
size = 1;
while(size <= n) size *= 2;
t.resize(2 * size, 0);
add.resize(2 * size, 0);
for (int i = 0; i < (int)a.size(); i++)
t[i + size] = a[i];
for (int i = size - 1; i > 0; i--)
t[i] = t[2*i]+t[2*i+1];
}
};

11. The main function of the method

void push(int v){
add[2*v]+= add[v];
add[2*v+1]+= add[v];
add[v] = 0;
}

12. The change request

void change(int v, int tl, int tr, int l, int r, int d){
if (l > r) return;
if (tl == l && tr == r){
add[v] += d;
return;
}
push(v);
int mid = (tl + tr) / 2;
change(2*v, tl, mid, l, min(r, mid), d);
change(2*v+1, mid + 1, tr, max(l, mid + 1), r, d);
t[v] = t[2*v] + (mid - tl + 1) * add[2*v] + t[2*v+1] + (r - mid) * add[2*v+1];
}
change(1, 0, size - 1, l, r, d);

13. Getting sum

int sum(int v, int tl, int tr, int l, int r){
if (l > r) return 0;
if (tl == l && tr == r){
return t[v] + add[v] * (r - l + 1);;
}
push(v);
int mid = (tl + tr) / 2;
int left_sum = sum(2*v, tl, mid, l, min(r, mid));
int right_sum = sum(2*v+1, mid+1, tr, max(l, mid+1), r);
t[v] = t[2*v] + (mid - tl + 1) * add[2*v] + t[2*v+1] + (r - mid) * add[2*v+1];
return left_sum + right_sum;
}
sum(1, 0, size - 1, l, r);

14. Useful links

• neerc.ifmo.ru:
1) Дерево отрезков. Построение
2) Реализация запроса в дереве отрезков сверху
3) Несогласованные поддеревья. Реализация массового обновления
• E-maxx. Дерево отрезков – описано большое количество задач,
которые решаются деревом отрезков с решением.
• Codeforces (Eng article)