Quasi-reproducible experiments: Universal fitting function for quantitative description of complex systems data

1. Quasi-reproducible experiments: Universal fitting function for quantitative description of complex systems data

Raoul R. Nigmatullin1),
Литвинов А.А.
1)Radio-electronics and
Informative Measurements
Technics Department,
Kazan National Research
Technical University (KNRTUKAI)
11.04.24-KNRTU-KAI
Нигматуллин Р.Р., Литвинов А,А и Осокин С.И.
ПОЧТИ-ВОСПРОИЗВОДИМЫЕ ЭКСПЕРИМЕНТЫ:
УНИВЕРСАЛЬНАЯ ПОДГОНОЧНАЯ ФУНКЦИЯ
ДЛЯ КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
СЛОЖНЫХ СИСТЕМ

2.

Аннотация
В данной работе изложены основы оригинальной теории квази-воспроизводимых
экспериментов (КВЭ), основанной на проверяемой гипотезе о существовании существенной
корреляции (памяти) между последовательными измерениями. На основе этой гипотезы, которую
авторы для краткости обозначают как принцип верифицированной частичной корреляции
(ВПЧК), можно доказать, что существует универсальная подгоночная функция (УПФ) для квазипериодических (КП) и квази-воспроизводимых (КВ) измерений. Другими словами, существует
некая общая платформа или "мост", на котором, образно говоря, встречаются истинная теория
(претендующая на описание данных из первых принципов или верифицируемых моделей) и
эксперимент, предлагающий эту теорию для проверки измеренных данных, максимально
"очищенных" от влияния неконтролируемых факторов и аппаратной функции измерительного
прибора. Предложенная теория была применена для анализа вихревых турбулентных массовых
потоков данных, связанных с измерениями соответствующих концентраций CH4, CO2 и водяных
паров H2O в атмосфере. Временная динамика концентраций этих газов регистрировалась на
соответствующих откалиброванных детекторах, специально предназначенных для измерения
содержания этих газов. В результате была получена АЧХ, соответствующая этим кумулятивным
данным и вычислены в рамках КВЭ необходимые количественные характеристики.
Эта теория может быть применена к широкому классу сложных систем, отклик которых может
быть многократно измерен. В качестве другого примера были рассмотрены данные по
космическому/реликтовому излучению, предоставленные одному их авторов (РРН) институтом
Макса Планка.
2

3.

Plan of my talk:
1. The motivation (creation new bridge
between experiment and theory)
2. The grounds of the general theory
3. Experiment (Complex systems: (1)
Eddy-covariance data - CH4,CO2, H2O;
Cosmic Rays)
4. Treatment of data
5. Results and Discussion + (2)ECG!
6. The remaining problems?
3

4.

The basic question: Is it possible to prove that any sampling of
the quasi-reproducible (QR)- measurements can generate a
“universal” fitting function?
If the answer can be positive then:
(a) It is not necessary to have an additional hypothesis (especially
for complex systems) – universal fitting standard!
(b) We’ll have a common bridge where the microscopic theory with
experiment can be reconciled with each other.
(c) Additional tool of the mathematical statistics for testing of
different suppositions (universal “fingerprint”)
(d) Conception of the self-similar experiment. Instead of detection
of the fractal properties – to impose fractal properties with the
help of specially prepared measurements to the system studied.
(e) Additional arguments based on real data
4

5.

1. The motivation
The general platform for reconciliation of the
Proposed Theory (Eva) with Experiment (Adam)
The way of an
Experiment He (Adam): (a)
set-up, (b)
accurate
measurements
(c) elimination
of the
uncontrollable
factors
The way of the
Theory –She
(Eva):
microscopic/
empirical
(properties of the
matter), the
“best-fit”
function.
Is it possible to create a new paradigm?
The conception of the intermediate model?
5

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

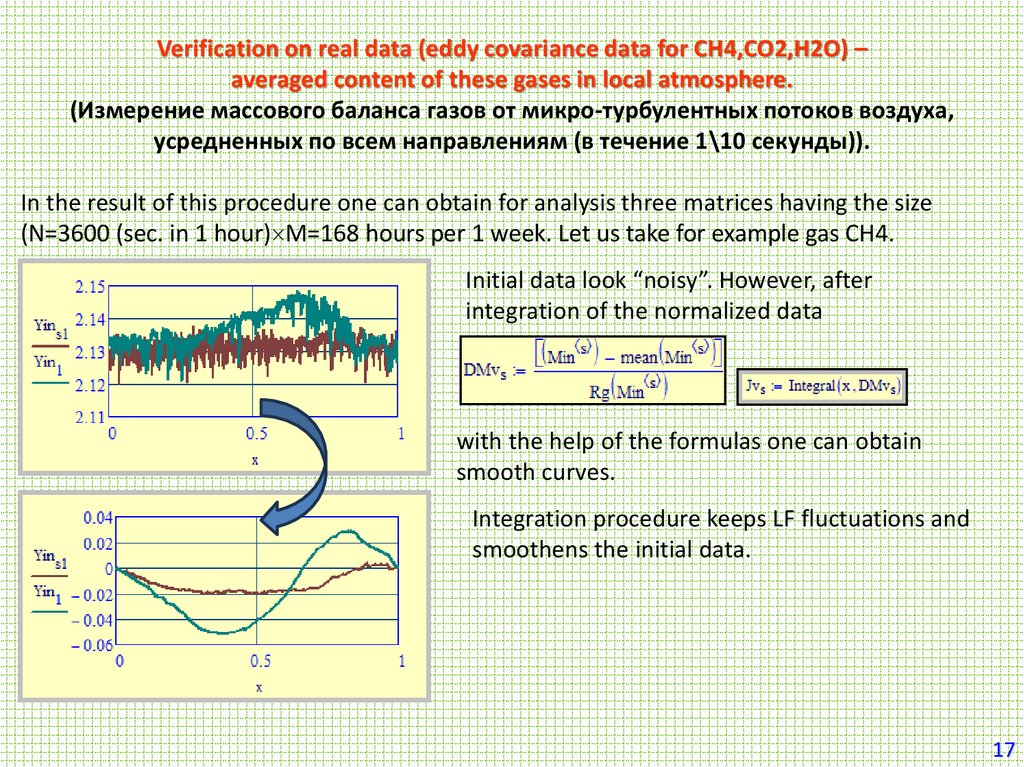
Verification on real data (eddy covariance data for CH4,CO2,H2O) –
averaged content of these gases in local atmosphere.
(Измерение массового баланса газов от микро-турбулентных потоков воздуха,
усредненных по всем направлениям (в течение 1\10 секунды)).
In the result of this procedure one can obtain for analysis three matrices having the size
(N=3600 (sec. in 1 hour) M=168 hours per 1 week. Let us take for example gas CH4.
Initial data look “noisy”. However, after
integration of the normalized data
with the help of the formulas one can obtain
smooth curves.
Integration procedure keeps LF fluctuations and
smoothens the initial data.
17

18.

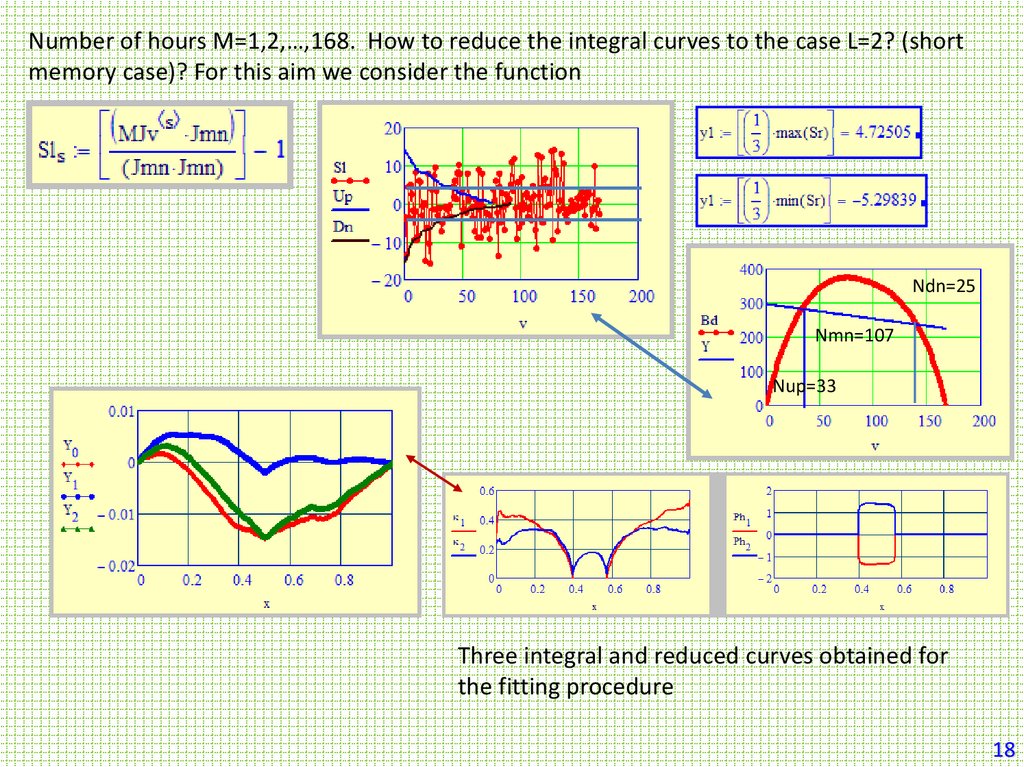
Number of hours M=1,2,…,168. How to reduce the integral curves to the case L=2? (short
memory case)? For this aim we consider the function
Ndn=25
Nmn=107
Nup=33
Three integral and reduced curves obtained for
the fitting procedure
18

19.

19

20.

20

21.

21

22.

22

23.

23

24.

24

25.

25

26.

26

27.

27

28.

28

29.

30.

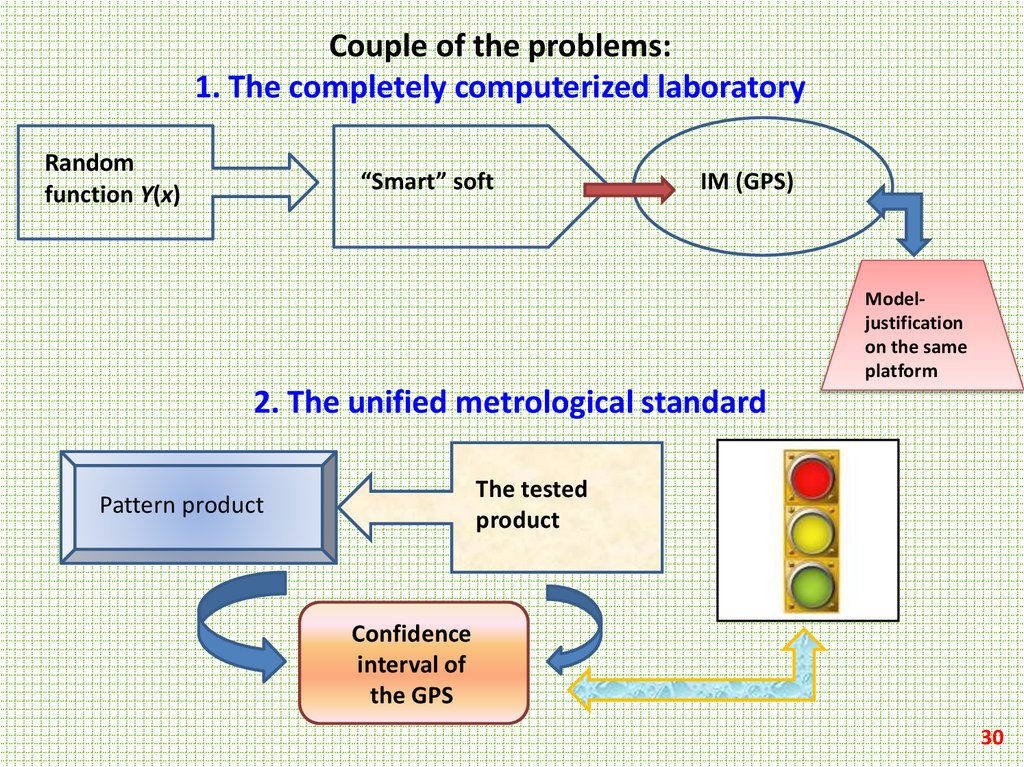
Couple of the problems:
1. The completely computerized laboratory
Random
function Y(x)
“Smart” soft
IM (GPS)
Modeljustification
on the same
platform
2. The unified metrological standard
The tested
product
Pattern product
Confidence
interval of
the GPS
30

31.

32.

33.

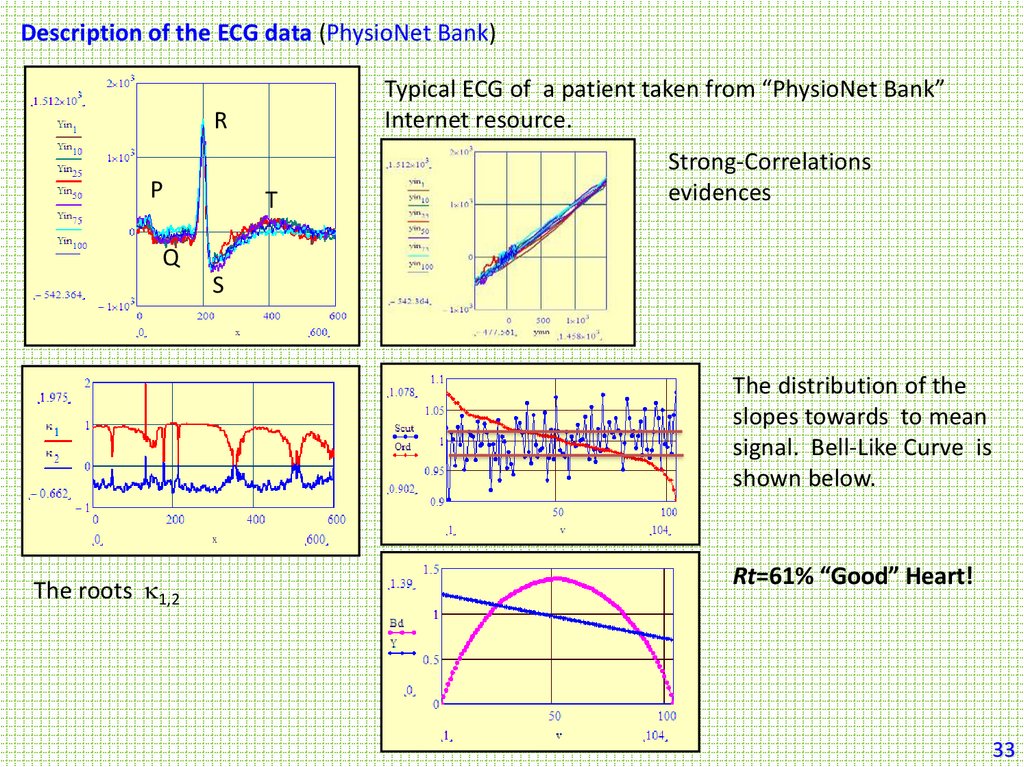
Description of the ECG data (PhysioNet Bank)
Typical ECG of a patient taken from “PhysioNet Bank”
Internet resource.
R
P
T
Strong-Correlations
evidences
Q
S
The distribution of the
slopes towards to mean
signal. Bell-Like Curve is
shown below.
The roots 1,2
Rt=61% “Good” Heart!
33

34.

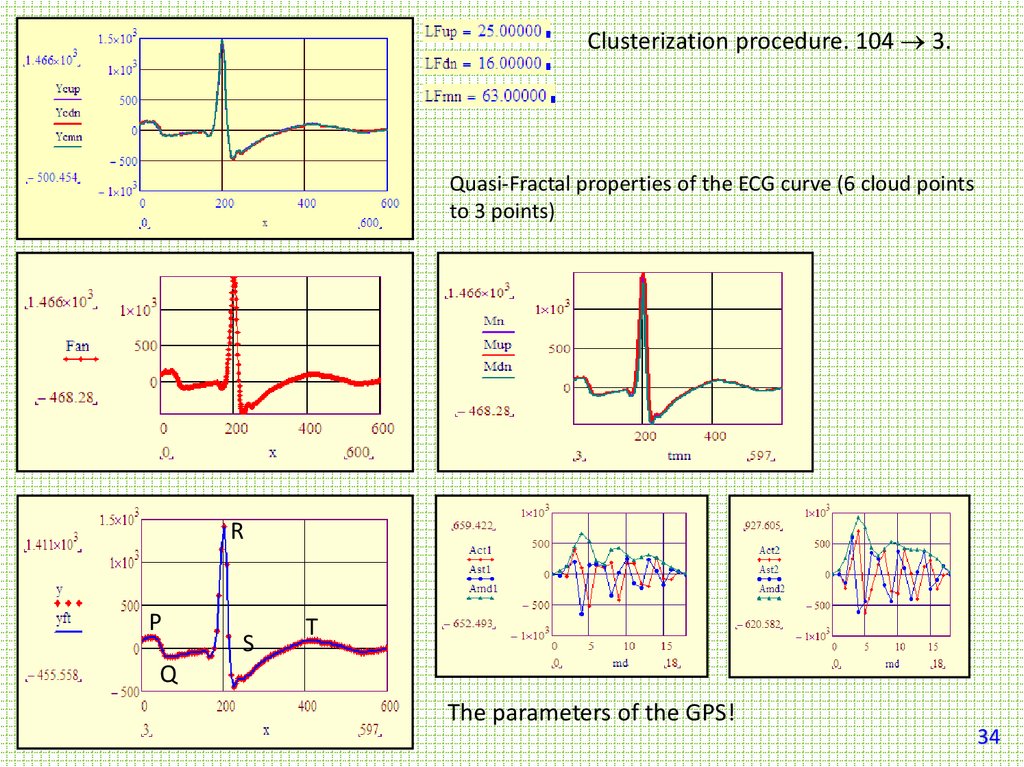
Clusterization procedure. 104 3.
Quasi-Fractal properties of the ECG curve (6 cloud points
to 3 points)
R
P
S
T
Q
The parameters of the GPS!
34

35.

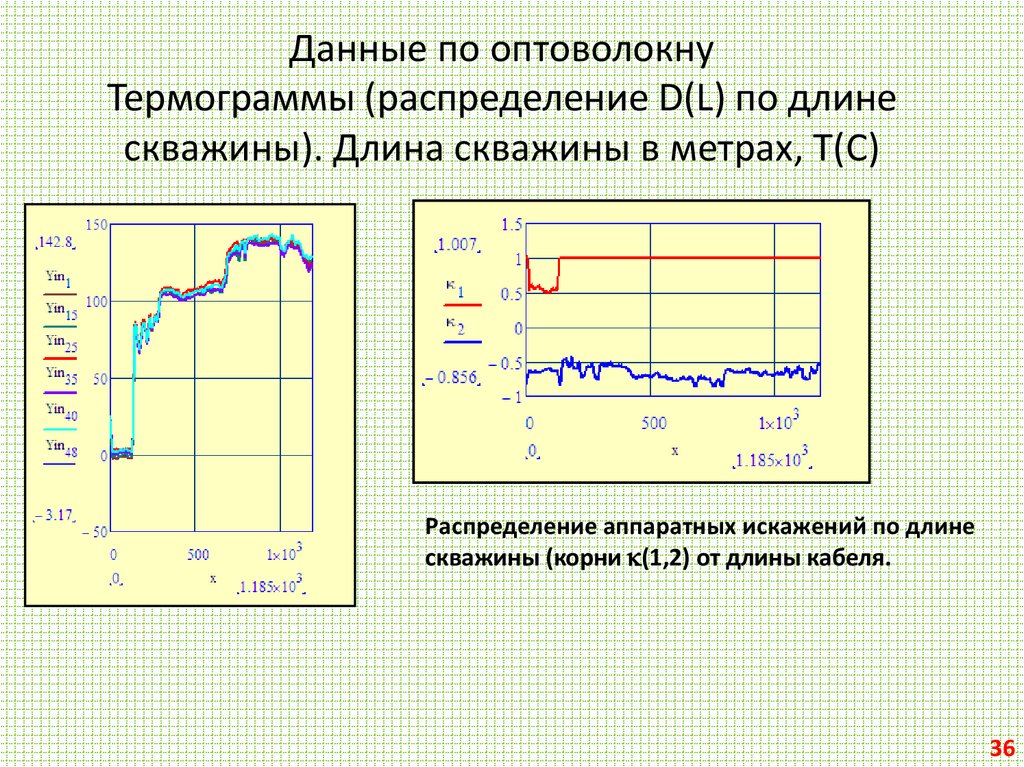
36. Данные по оптоволокну Термограммы (распределение D(L) по длине скважины). Длина скважины в метрах, Т(С)

Распределение аппаратных искажений по длине
скважины (корни (1,2) от длины кабеля.
36

37.

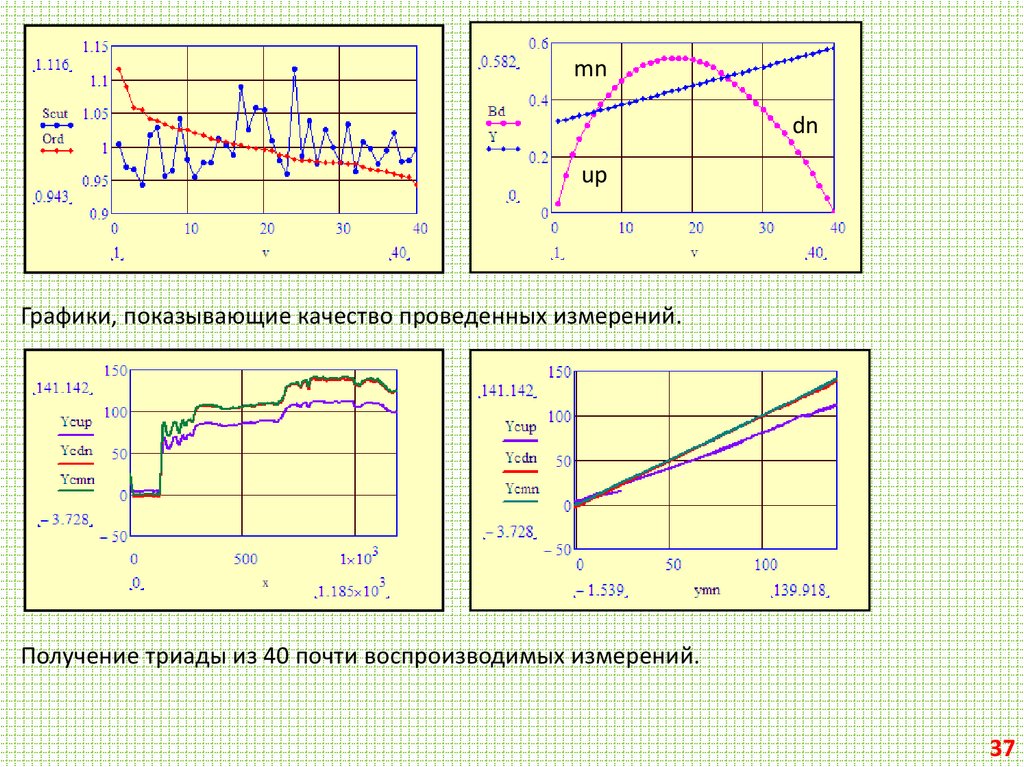
mn
dn
up
Графики, показывающие качество проведенных измерений.
Получение триады из 40 почти воспроизводимых измерений.
37

38.

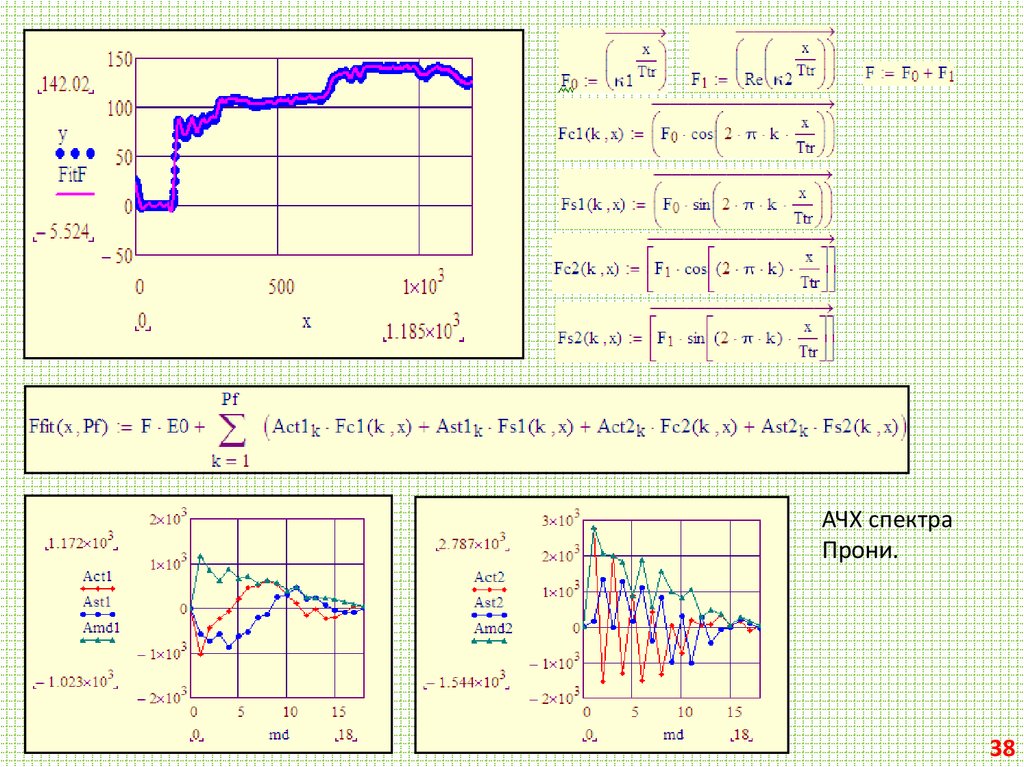
АЧХ спектра
Прони.
38

39.

References
[1] R.R. Nigmatullin, W. Zhang and D. Striccoli. General theory of experiment containing
reproducible data: The reduction to an ideal experiment. Communications in Nonlinear
Science and Numerical Simulation, 27, (2015), pp 175-192.
[2] L.R. Rabiner and B. Gold, "Theory and application of digital signal processing". Englewood
Cliffs, NJ, Prentice-Hall, Inc., 1975.
[3] Singleton Jr, A. Royce, B.C. Straits, and M. M. Straits, "Approaches to social research".
Oxford University Press, 1993.
[4] J. M. Mendel, "Lessons in estimation theory for signal processing, communications, and
control". Pearson Education, 1995.
[5] M.T. Hagan, H. B. Demuth and M. H. Beale, "Neural network design". Boston: Pws Pub.,
1996.
[6] E.C. Ifeachor, and B.W. Jervis, "Digital signal processing: a practical approach". Pearson
Education, 2002.
[7] D.C. Montgomery, C.L. Jennings and M. Kulahci, "Introduction to time series analysis and
forecasting". John Wiley & Sons, 2011.
[8] J.S. Bendat and A.G. Piersol, "Random data: analysis and measurement procedures". John
Wiley & Sons, 2011.
[9] A. Gelman, J.B. Carlin, H.S. Stern, D.B. Dunson, A. Vehtari and D.B. Rubin, "Bayesian data
analysis". CRC press, 2013.
[10] G. E.P. Box, G.M. Jenkins and G.C. Reinsel, "Time series analysis: forecasting and control".
John Wiley & Sons, 2013.
[11] C. Chatfield, "The analysis of time series: an introduction". CRC press, 2013.
39

40.

[12] R. Nigmatullin, R. Rakhmatullin. Detection of quasi-periodic processes in repeatedmeasurements: New approach for the tting and clusterization of different data.
Communications of Nonlinear Science and Numerical Simulation 19 (2014) pp. 4080-4093.
[13] R.R. Nigmatullin, A.A. Khamzin and J. T. Machado, Detection of quasi-periodic
processes in complex systems: how do we quantitatively describe their properties? Physica
Scripta 89 (2014) 015201 (11pp).
[14] Raoul R. Nigmatullin, Sergey I. Osokin, Dumitru Baleanu, Sawsan Al-Amri, Ameer
Azam, Adnan Memic, The First Observation of Memory Effects in the InfraRed (FT-IR)
Measurements: Do Successive Measurements Remember Each Other? PLoS ONE, Open
access journal, April 9 (4) (2014) e94305.
[15] Raoul R. Nigmatullin, José Tenreiro Machado, Rui Menezes. Self-similarity principle: the
reduced description of randomness. Central European Journal of Physics. 11(6) (2013) P 724739. (DOI: 10.2478/s11534-013-0181-9).
[16] R.R. Nigmatullin, R.M. Rakhmatullin, S.I. Osokin, How to reduce reproducible
measurements to an ideal experiment? Magnetic Resonance in Solids, Electronic Journal,
(2014) 16 (2) pp.1-19. http://mrsej.kpfu.ru.
40

41.

41