Предикат. Логические операции над предикатами

1.

ПРЕДИКАТ. ЛОГИЧЕСКИЕ
ОПЕРАЦИИ НАД
ПРЕДИКАТАМИ.

2.

1. Понятие предиката
Логика
предикатов
расчленяет
элементарное
высказывание
на
субъект
(буквально
—
подлежащее, хотя оно и может
играть
роль
дополнения)
и
предикат (буквально - сказуемое,
хотя оно может играть и роль
определения).

3.

Субъект — это то, о чем что-то
утверждается
в
высказывании;
предикат
это
то,
что
утверждается о субъекте.
Например,
Студент слушает
лектора
субъект
предикат
объект

4.

Пример:
В высказывании «7 - простое число», «7»
-субъект, «простое число» - предикат. Это
высказывание утверждает, что «7» обладает
свойством «быть простым числом».
Если в рассмотренном примере заменить
конкретное число 7 переменной х из
множества натуральных чисел, то получим
высказывательную форму «х - простое
число». При одних значениях х, (например, х
= 13, х =17 ) эта форма дает истинные
высказывания, а при других значениях х
(например, х = 10 , х = 18 ) эта форма дает
ложные высказывания.

5.

Определение
□ Функция Р(х1, х2,…, хn), переменные
которой
х1, х2,…, хn имеют своими
значениями
элементы
некоторого
множества
D,
обращающаяся
в
высказывание
для
каждой
n-ки
элементов
этого
множества,
называется n-местным предикатом,
или
n-местной
пропозициональной
функцией.

6.

Сопоставляя
с
каждым
высказыванием-значением предиката
Р(х1, х2,…, хn)- его истинностное
значение. Мы обнаружим. Что со
всяким
таким
предикатом
связывается функция вида Mn И,Л

7.

Например:
С предикатом «х написал роман
«Мать»» связывается функция вида
M И,Л , где М-множество людей;
с
предикатом
х+2у=23
–
функция вида R2 И,Л , где R2 множество
пар
действительных
чисел.

8.

Одноместным предикатом Р(х)
называется произвольная функция
переменного х, определенная на
множестве
М
и
принимающая
значения из множества {1,0}.

9.

Определение
□ Функция вида Mn И,Л называется nместной
логической
функцией.
Множество Dn называется областью
определения логической функции,
множество И,Л -областью значений
логической функции, множество I Dn,
на
котором
функция
принимает
значение И,-областью истинности
логической функции.

10.

Область определения
Множество М, на котором определен
предикат
P(х),
называется
областью
определения
предиката.

11.

Множество всех элементов х ∈ М ,
при которых предикат принимает
значение
«истина»,
называется
множеством
истинности
предиката Р(х).

12.

Например:
Р(х) - «х - простое число» определен на
множестве N, а множество истинности для
него есть множество всех простых чисел.
Предикат Q{x} - « sin х = 0 » определен на
множестве R, а его множество истинности -Q.
Предикат
F(x)
«Диагонали
параллелограмма
перпендикулярны»
определен
на
множестве
всех
параллелограммов,
а
его
множеством
истинности является множество всех ромбов.

13.

Предикат Р(х), определенный на
множестве
М,
называется
тождественно истинным ,если
область определения предиката и
область истинности совпадают.

14.

Задание 1
Для следующих предложений
выделить предикаты и для каждого
из них указать область истинности:
■ х+5=1;
■ х+2<3x – 4;
■ однозначное число х кратно 3;

15.

Задание 2
Изобразить на декартовой
плоскости области истинности
предикатов:
■ х+у=1;
■ х+3у=3;
■ ((x>2)v(y>1))((x<-1)v(y<-2)).

16.

2.Ионы и переменные
Подобно
тому,
как
в
алгебре
высказываний мы допустили в предметном
языке предложений, выражающих на этом
языке элементарные формулы, или атомы,
теперь будем считать. Что изучаемый
предметный язык располагает средствами
для
выражения
предикатов
любой
местности. Такие выражения назовем
элементарными
предикатными
выражениями или ионами.

17.

Ионы и переменные
Обозначения ионов:
• P,Q,R,…,X ,Y-нульместные ионы;
• Q(-),R(-),…,X(-),… -одноместные ионы;
• P(-,-), Q(-,-) –двухместные ионы и т.д.
Понятно, что подобных обозначений
для
любого
ненульместного
иона
имеется бесконечное множество.

18.

Называющая форма иона
Под
называющей
формой
иона
понимают
его
обозначение
с
использованием
переменных.
Таким
образом. Каждый ион имеет бесконечное
множество называющих форм.Например,
2x=5,
2у=5,
2z=5
и
т.п.Следует
отметить, что записи R(x,x,у), Q(x,у,х)
или Q(у,у,х) не являются называющими
формами для трехместного иона, т.к.
они не элементарны.

19.

Атомы
□ Если А(-,…,-) –любой n-местный
ион,а х1, х2,…, хn –произвольный
набор
n
переменных,
не
обязательно различных, то
А(х1, х2,…, хn) – атом алгебры
предикатов.
.

20.

Атомы
• Ясно, что любой нульместный ион,
например R, порождает только один
атом R. Исходя из иона R(-), получим
атомы R(х), R(у), R(z) и т.д.
• Если n 1, то атомы образуют более
широкий класс по сравнению с
называющими формами ионов, т.к.
переменные, заполняющие пустые
места, не обязательно различны.

21.

Алфавит алгебры предикатов
□ Определение.
Алфавитом алгебры предикатов
называется
множество
Аа.п.,содержащее
буквы
для
обозначения: ионов, переменных,
логических операций ( , , , , , , ),
а также буквы скобки (,), и только
эти буквы.

22.

Формулы алгебры предикатов
а)Всякий
атом–формула(элементарная
формула).
б)Если А-формула, то ( А) –формула.
в)Если А и В –формулы, то (А В), (А В),
(А В), (А В) –формулы.
г)Если А-формула, а а-переменная, то
( аА) и ( аА) –формулы.
д)Других формул, кроме указанных в
пункте а) и построенных по правилам
пунктов б), в), г), нет.

23.

Формулы алгебры предикатов
Для упрощения записей формул
сохраним
соглашение
алгебры
высказываний об опускании скобок.
Дополнив его следующим –
• унарные
операторы
и
выполняются раньше оператора .
Например,
формула
х Р(х) Q(х)
означает
( х Р(х)) Q(х),
а
не
х( Р(х) Q(х)).

24.

□ На
этом
этапе
необходимо
обратиться к Приложению 3 и
разобрать предложенные примеры.

25.

Семантика букв алфавита
алгебры предикатов
□ Значения
букв
алфавита
Аа.п.
в
классической двузначной логике:
□ 1. Буквы первой категории – переменные
p,q,r,…,y,z,…(или
Cnst
—
множество
констант). Их смысл зависит от того, к
какой
области
науки
относятся
рассматриваемые ионы. Допустим, что
существует
непустое
множество
М,
называемое предметной областью, из
которой
черпают
свои
значения
переменные, называемые предметными
переменными.

26.

Семантика букв алфавита
алгебры предикатов
□ 2. Буквы второй категории – ионы
P,Q,…,P(-),Q(-),P(-,-),…,Y(-,-,-),…
□ Ионы
являются
средствами
выражения
предикатов.
Т.е.
значениями ионов являются
всевозможные
логические
функции.
*Семантика –это свод правил, наделяющих значением (смыслом)
синтаксические конструкции языка.

27.

Пример 1.
□
Пусть
одноместный
ион
«х-простое
число»
рассматривается на предметной области М – множество N
натуральных
чисел.
Какой
логической
функцией
характеризуется этот ион?
Решение. Первые значения этой логической функции
приведены в таблице:
х
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
l(x)
Л
И
И
Л
И
Л
И
Л
Л
Л
И
Л
И
Л
Л
Логическая функция l(x)–бесконечный объект. кроме
указанных в таблице значений логической функции, можно
выписать еще некоторые: l(100)=Л, l(313)=И, l(317)=И.

28.

□ Замечание.
Если
предметная
область М конечна, то тогда
логическая функция l(х1, х2,…, хn )
– также конечный объект и
множество n-местных логических
функций –конечное множество.
которое может быть выписано.

29.

Пример 2:
□ Указать значения нульместных
ионов на любой предметной
области.
□ Решение. Ими являются И либо Л,
т.е. множество значений
нульместного иона есть множество
И,Л .

30.

Пример 3:
□ Пусть предметная область М= 1,2 . Какие значения
имеет двухместный ион A(a,b) на этой области?
□ Решение.Значение такого иона есть логическая
функция, сопоставляющая с каждым из четырех
возможных наборов значений переменных a и b –
(1,1),(1,2),(2,1),(2,2) – элемент множества И,Л .
Каждое такое сопоставление есть размещение с
повторениями из лвух элементов множества И,Л
по 4, т.е. число различных двухэлементных
логических функций на двухэлементной области М=
1,2 равно 24, т.е. имеет 16 различных значений,
выписанных в таблице.

31.

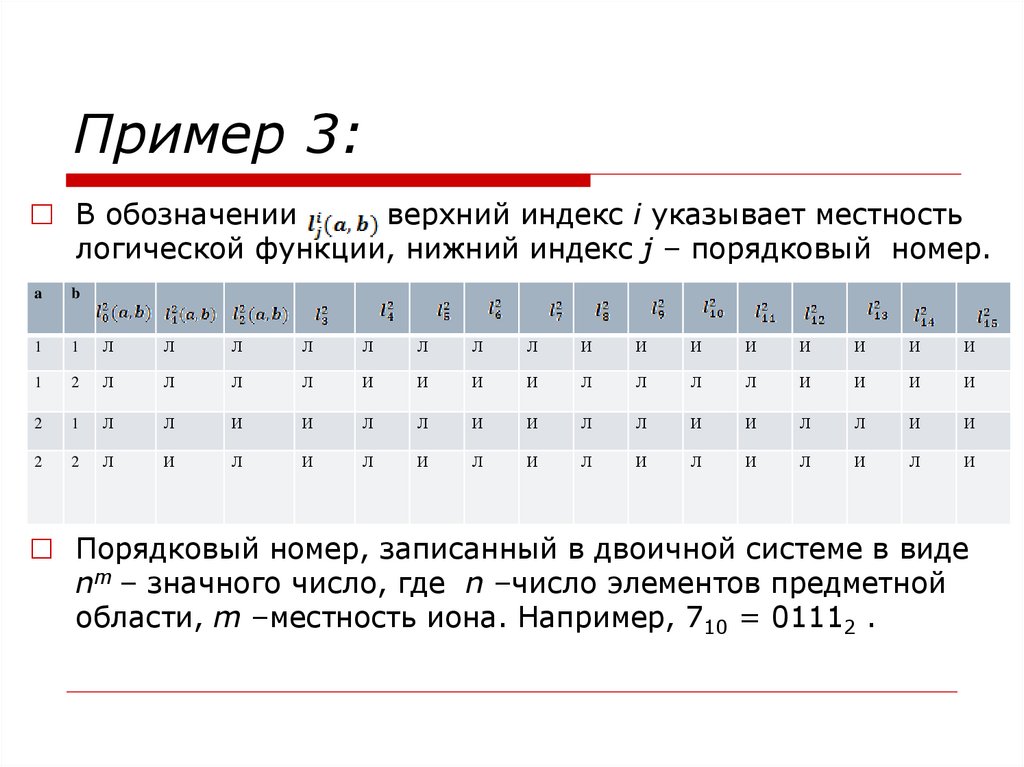
Пример 3:
□ В обозначении
верхний индекс i указывает местность
логической функции, нижний индекс j – порядковый номер.
a
b
1
1
Л
Л
Л
Л
Л
Л
Л
Л
И
И
И
И
И
И
И
И
1
2
Л
Л
Л
Л
И
И
И
И
Л
Л
Л
Л
И
И
И
И
2
1
Л
Л
И
И
Л
Л
И
И
Л
Л
И
И
Л
Л
И
И
2
2
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
□ Порядковый номер, записанный в двоичной системе в виде
nm – значного число, где n –число элементов предметной
области, m –местность иона. Например, 710 = 01112 .

32.

Семантика букв алфавита
алгебры предикатов
□ 3. Буквы третьей категории –знаки
логических операций , , , , , , .
Истинностные
таблицы
для
операций
, , , , ,
с
помощью
которых
вычисляются
истинностные
значения
молекул
в
алгебре
высказываний, сохраняют силу и в
алгебре предикатов.

33.

Семантика букв алфавита
алгебры предикатов
□ Например, пусть в некоторой предметной области М
формулы А(а) и В(а) характеризуются логическими
функциями li(а) и lj(а) соответственно. Тогда формула
А(а) В(а) характеризуется логической функцией li(а) lj(а),
принимающей значение И при всех тех и только тех
значениях а, при которых значение И имеет как логическая
функция li(а), так и lj(а).
□ Область истинности логической
lj(а)
li(а)
функции, характеризующей формулу
А(а) В(а), можно изобразить диаграммой
Венна.

34.

Семантика букв алфавита
алгебры предикатов
□ 4.
Буквы четвертой категории –
скобки (,) – самостоятельного смысла
не имеют, и играют роль знаков
препинания.

35.

3. Логические операции над
предикатами
□ Предикаты,
так
же,
как
высказывания,
принимают
два
значения истина и ложь 1, 0 ,
поэтому к ним применимы все
операции логики высказываний.
* См. учебник М.С. Спирина, М.С. Спирин ДИСКРЕТНАЯ МАТЕМАТИКА, стр. 227

36.

□ Конъюнкцией двух предикатов
Р(х) и Q(x) называется новый
предикат
Р(х)ΛQ{x),
который
принимает значение «истина» при
тех и только тех значениях х ∈ М,
при которых каждый из предикатов
принимает значение «истина», и
принимает значение «ложь» во всех
остальных случаях.
* Рисунок см. учебник М.С. Спирина, М.С. Спирин ДИСКРЕТНАЯ МАТЕМАТИКА, стр.
227

37.

Пример:
Для предикатов Р(х): «х – четное
число» и Q(x): «х кратно 3»
конъюнкцией P(x)ΛQ(x) является
предикат «х - четное число и х
кратно 3», то есть предикат «х
делится на 6»

38.

□ Дизъюнкцией двух предикатов Р(х) и
Q(x) называется предикат
Р(х)V
Q(x), определенный на множестве D,
который принимает значение «ложь»
при тех и только тех значениях х ∈ М,
при которых каждый из предикатов
принимает
значение
«ложь»
и
принимает значение «истина» во всех
остальных случаях.
□ * Рисунок см. учебник М.С. Спирина, М.С. Спирин ДИСКРЕТНАЯ МАТЕМАТИКА, стр.
229

39.

Отрицанием
предиката
Р(х)
называется новый предикат Р(х) ,
который принимает значение «истина»
при всех значениях х ∈ М, при которых
предикат Р(х) принимает значение
«ложь», и принимает значение «ложь»
при тех значениях х ∈ М, при которых
предикат Р(х) принимает значение
«истина».
* Рисунок см. учебник М.С. Спирина, М.С. Спирин ДИСКРЕТНАЯ МАТЕМАТИКА, стр. 227

40.

□ Импликацией предиката Р(х) в
Q(x)
называется
предикат
Р(х) Q(x), определенный на
множестве D, который принимает
значение «ложь» при тех и только
тех значениях х ∈ D, при которых
предикат Р(х) истинен, а предикат
Q(x) ложен.
* Рисунок см. учебник М.С. Спирина, М.С. Спирин ДИСКРЕТНАЯ МАТЕМАТИКА, стр.
229

41.

□ Например, импликацией предикатов
Р(х): «х-нечетное число» и Q(x): «х
кратно 5», определенных на
N 0 ,служит предикат
Р(х) Q(x): «Если х-нечетное число,
то х кратно 5».

42.

□ Эквиваленцией предикатов Р(х) и
Q(x)
называется
предикат
Р(х) Q(x),
определенный
на
множестве D, который принимает
значение «истина» при тех и только
тех значениях х ∈ D, при которых
либо оба предиката истинны, либо
оба предиката ложны.

43.

Требования оформления
конспекта (рабочей тетради)
□ Наличие теоретического материала в полном объеме
□
□
□
□
□
(представлен в виде схемы, тезауруса и т.п.);
Иерархия в записи материала (первичные понятия,
определения, выводы, практика);
Темы идут в поступательном порядке (например, первая
тема не может быть записана в конце тетради, т.
«дописана»);
Наличие домашнего задания в полном объеме (запись
условия, решения, ответа обязательны!);
Тетрадь представлена по одной дисциплине (не разные
записи в одной тетради);
Тетрадь имеет только записи по дисциплине (не
содержит заметоко и рисунков к ней неотносящихся);
имеет опрятный вид.