Similar presentations:
Золотое сечение
1. Золотое сечение
2. Эпиграф к уроку
О сколько нам открытийчудных
Готовит просвещенья дух,
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог- изобретатель.
А . С. Пушкин
3. Цель и задачи урока
Цель урока – показать связь математики с другими предметамиЗадачи :
Познакомить с понятием «Золотое сечение».
Вывести формулу «золотого» сечения
Показать применение «золотого» сечения в других областях
Расширение кругозора учащихся, обогащение знаниями
об общекультурных ценностях человечества.
Популяризация новейших информационных технологий.
4. содержание
Основатели учения о золотом сеченииПонятие золотого сечения
Золотое сечение в архитектуре
Золотое сечение в живописи
Золотое сечение в живых организмах
Правильный пятиугольник
Самый «правильный» многогранник
Золотое сечение вокруг нас
Список используемой литературы
5. «Довольно почестей Александрам! Да здравствуют Архимеды!» Сен-Симон А.
Пифагор (580-500 г.г.до н.э.)Евдокс (408 – ок.355 г.г.до н.э.)
Леонардо да Винчи (1452-1519 г.г.)
Пропорции, т.е. равенства
отношений изучались
пифагорейцами.
Евдокс развил учение о
пропорциях–одно из
величайших достижений
греческой математики.
Термин «золотое сечение»
ввёл Леонардо да Винчи.
6.
7. Квадратные уравнения и «формула красоты»
При решении различных ситуаций мы часто используемвыражение : «Здесь нужна «золотая» середина» . Возникает вопрос
о том , чем отличается просто середина отрезка от «золотой»?
Если отрезок разделить на 2 равные части , то рисунок будет
стационарным , неживым ;
если точку поставить близко к одному из концов отрезка , то рисунок
будет неуравновешенным ;
но есть такое положение точки , которое создает гармонию .
А
С
ОС : ОА = АО: АС
Такое соотношение частей древние греки называли
«золотой» пропорцией.
8. Золотое сечение – гармоническая пропорция
Золотое сечение – это такое пропорциональноеделение отрезка на неравные части, при котором весь
отрезок так относится к большей части, как сама
большая часть относится к меньшей; или другими
словами, меньший отрезок так относится к большему,
как больший ко всему
a : b = b : c или с : b = b : а.
9.
Как найти «золотую» серединуотрезка ?
Найдем численное значение «золотой» пропорции.
Для этого составим уравнение.
Пусть АС =1 , АО = Х, тогда ОС = 1-Х ;
составим пропорцию: Х : 1 = (1-Х ) : Х ;
отсюда получим квадратное уравнение :
Х² + Х -1 = 0 .
D = 1- 4* 1 *(-1)= 5 ;
Х¹ =( -1+√5)/2 ;
Х² =(-1-√5 )/2,
Х² < 0 .
Для удобства значение Х¹ записывают как :
Приблизительное значение равно 0,62
5 1
2
10. Как разделить отрезок в соответствии с «золотой» пропорцией?
ХК
Р
5
Х
Х(√ 5-1)
А
В
С
2Х
11.
СD
А
=
=
=
В
E
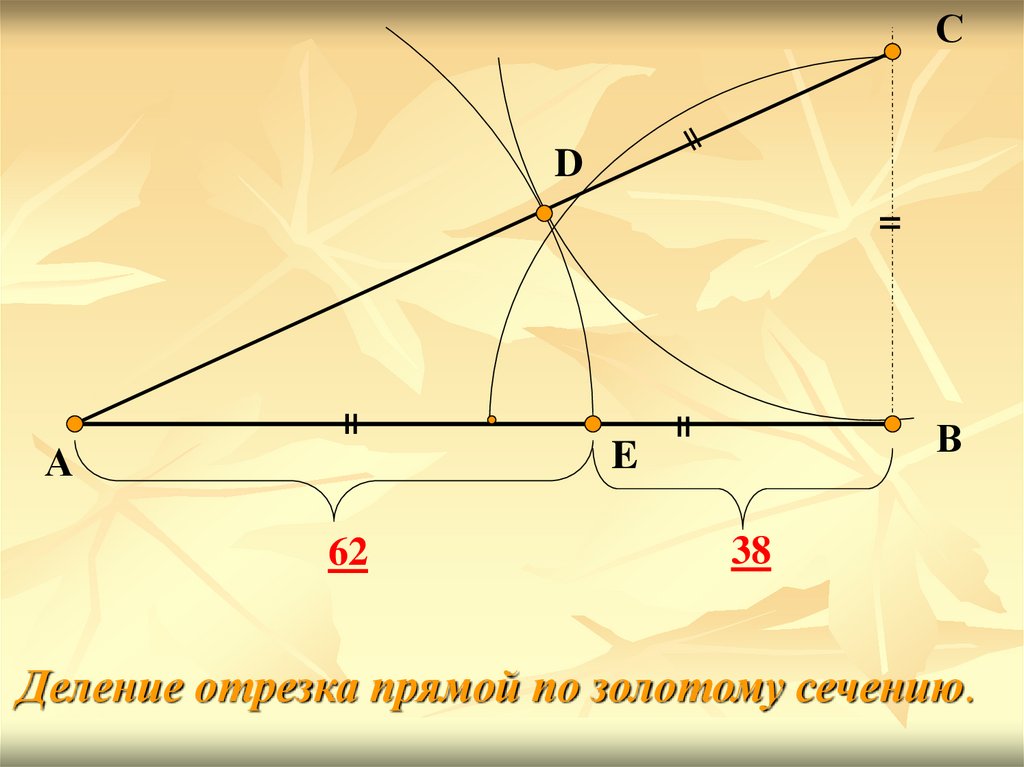
62
38
Деление отрезка прямой по золотому сечению.
12. «Сравнение математических фигур и величин служит материалом для игр и обучения мудрости» Песталоцци И.Г.
AB DEарифметическое среднее;
2
AD AB DB геометрическое среднее;
2 AB ED
AD
гармоническое среднее.
AB ED
AD
Определение золотого сечения:
целое относится к его большей
части так же, как большая часть
относится к меньшей части.
Отрезок АВ так относится к его
большей части AD, как эта
большая часть AD относится к
его меньшей части DB.
Иначе говоря, точка D делит
отрезок AB в «золотой
пропорции».
13. Золотое сечение и гармония
объекты, содержащие в себе «золотоесечение», воспринимаются людьми как
наиболее гармоничные
14. Число φ
Число (√5-1)/2обозначают греческой
буквой φ ,
в честь греческого
архитектора Фидия,
жившего в V веке до
н.э. и руководившего
строительством храма
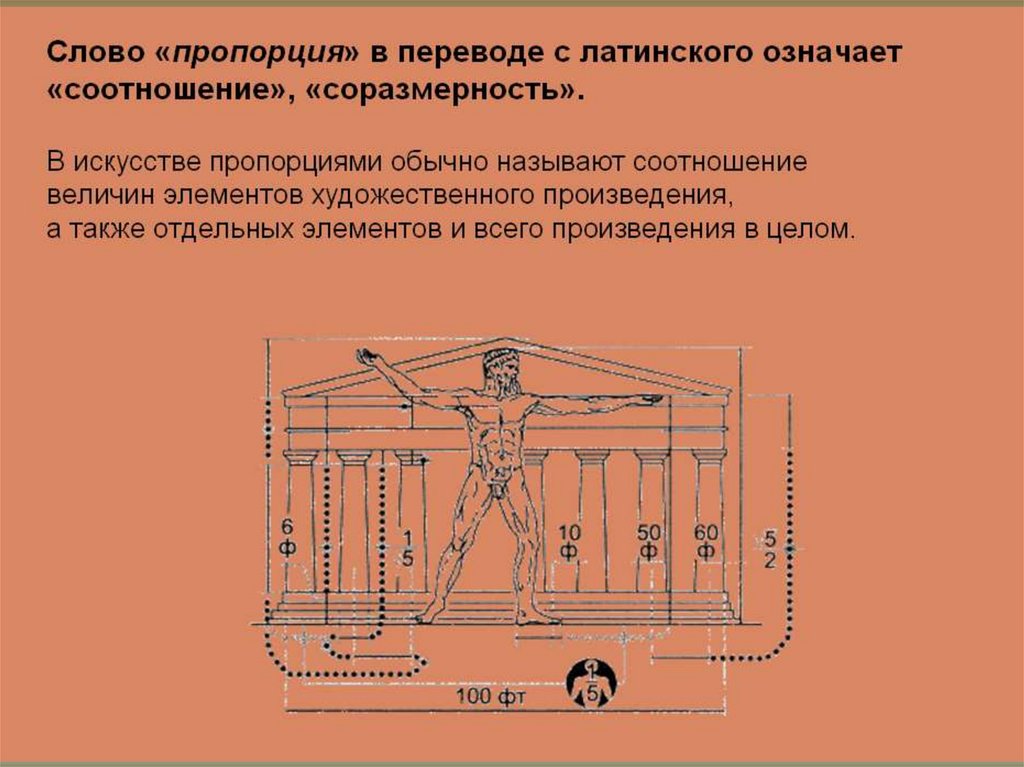
Парфенон в Афинах .
15.
16.
Отношение длины зданияПарфенона в Афинах к его
высоте равно Ф (фи).
КВ: АВ = СВ :АС= АВ:ВС
= φ.
17.
18. Пентаграмма
Первая фигура , известнаячеловеку ,
где встречается
«золотая» пропорция –
это пентаграмма.
Пифагор увидел этот знак
в Египте, где она
считалась амулетом
здоровья .
И великий математик
выбрал звезду символом
своей школы.
19. «Ни тридцать лет ни тридцать столетий не оказывают никакого влияния на ясность или на красоту геометрических тел» Кэррол Л.
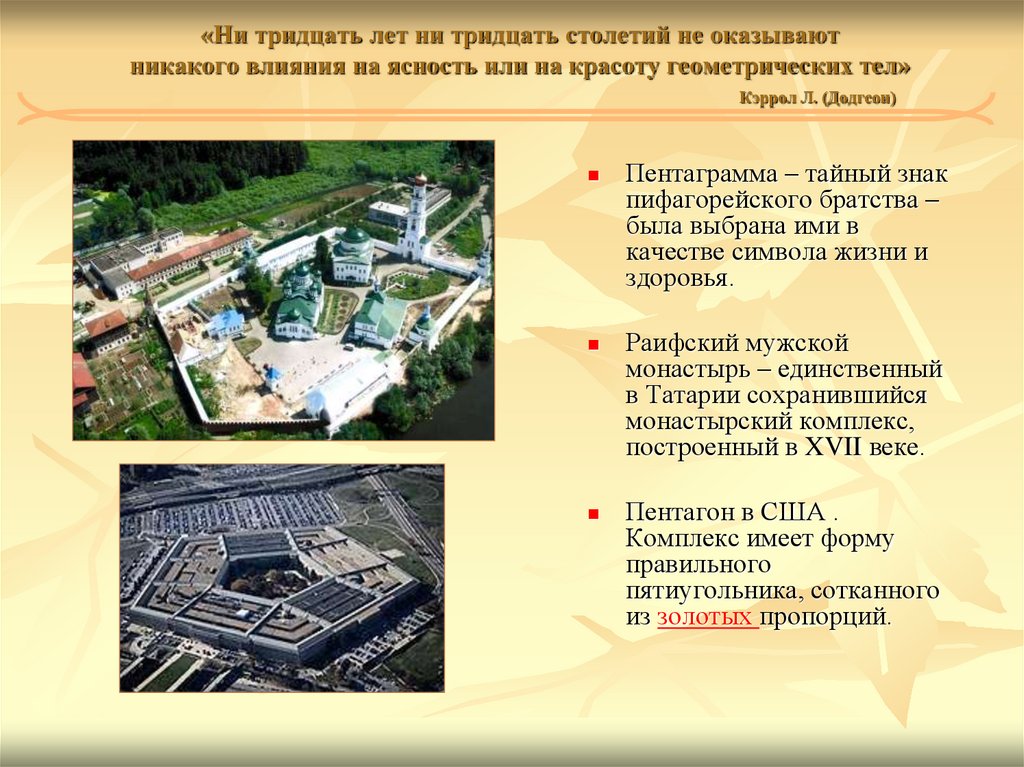
(Додгсон)Пентаграмма – тайный знак
пифагорейского братства –
была выбрана ими в
качестве символа жизни и
здоровья.
Раифский мужской
монастырь – единственный
в Татарии сохранившийся
монастырский комплекс,
построенный в XVII веке.
Пентагон в США .
Комплекс имеет форму
правильного
пятиугольника, сотканного
из золотых пропорций.
20.
21. φ и человек
«Человек-мера всех вещей» это знаменитый афоризм древнегреческого философаПротагора(490-420 г.до н.э.)
Как ни парадоксально, но между живыми линиями
человеческого тела и каменными сооружениями
существует глубокая математическая связь. .
Закономерность и красота мироздания
раскрывалась перед греками
и в симметрии живых организмов,
и в пропорциональности человеческого тела,
и в ритмах чередования дня и ночи ,
и смены времен года и т. д.
22. Вся античная архитектура и скульптура воплощали в себе эти принципы красоты. Блестящими примерами тому служат и величественные
пропорции Парфенона,и знаменитый «Канон»
Поликлета –
скульптура и
теоретический трактат,
в которых автор
попытался воплотить
идеальные, по его
мнению, пропорции
мужского тела.
23. φ и человек
Человеческое тело буквально пронизаночислом φ.
Так наша талия находится на линии «золотой»
пропорции ,
глаза находятся на уровне , которое делит наше
лицо в отношении φ.
«Золотую» пропорцию можно найти у себя на
руке.
Для этого измерьте длину двух фаланг своего
среднего пальца и поделите на длину всего
пальца .
Их отношение примерно 0,6 или число φ
24.
25.
26. Золотое сечение и зрительные центры
Золотое сечение и зрительные центрыДругим примером
использования правила "Золотого
сечения" - расположение
основных компонентов кадра в
особых точках - зрительных
центрах, Таких точек всего
четыре, и расположены они на
расстоянии 3/8 и 5/8 от
соответствующих краев
плоскости.
Человек всегда акцентирует
свое внимание на этих точках,
независимо от формата кадра или
картины.
27. «ФИ» в биологии
Иоганн Кеплер –математик и
астроном
обнаружил золотую
пропорцию у
растений .
28. Цикорий
Почему одно растениерадует глаз своей красотой,
почему растет здоровым?
Измерения показали , что
новые побеги появляются в
соответствии с золотым
сечением, поэтому растение не
гибнет, а тянется в верх.
При нарушении пропорции
растение гибнет.
Цикорий
29.
У головоногого моллюска –Наутилуса- соотношение
диаметра каждого витка спирали
к следующему =φ.
Аналогичное соотношение
наблюдается в подсолнечнике,
где семечки располагаются по
спирали против часовой стрелке,
в спиралеобразно закрученных
листьях початка кукурузы,
в сегментационных частях тел
насекомых .
30.
В ящерицес первого взгляда
улавливаются
приятные для
нашего глаза
пропорции –
длина ее хвоста так
относится к длине
остального тела,
как 62 к 38.
31. Золотые пропорции яйца
При измерении размеров отдельных элементов яйцаобнаруживается, что их части имеют зависимости от
Ф.
32. «Пристальное и глубокое изучение природы есть источник самых плодотворных открытий математики» Фурье Ж.
18 111.6
11 7
а b a b
1,6
a
b c
пропорции, близкие к золотому сечению.
33. φ в живописи
С наступлением эпохи Возрождения художники вновьобратились к классическим законам искусства.
Были нарушены основные запреты : изображать
реального человека; пространственное изображение;
воспевать красоту человеческого тела .
Первым таким художником был итальянский художник
Боттичелли.
Картина
“Рождение
Венеры”
около
1483 – 1484 г.
34.
35.
36.
Большой вклад в изучениеклассических правил искусства внес
самый гениальный человек Леонардо да
Винчи .
Проводя многочисленные
исследования в различных науках :
химии, физике, биологии , анатомии,
изучая поэзию, музыку, архитектуру и
живопись , он пришел к выводу, что
многие законы природы пронизаны
«золотой»пропорцией или ,как он писал
в своих исследованиях- «золотым»
сечением .
Как художник он пошел дальше
Боттичелли , т.к. на его картинах
изображены не символы , а реальные
люди .
37.
При создании своихкартин Леонардо
пользовался правилом
«золотого» сечения.
Отношение длины
полотна к высоте равна
числу φ.
Линия горизонта
находится на уровне
линии «золотого» сечения.
Да и сама Мона Лиза
заключена в «золотой»
треугольник .
38.
ДжокондаЛеонардо
да Винчи
39.
38Леонардо
да Винчи
Мадонна
62
с
младенцем
40.
6238
И.Шишкин «Рожь»
41. “Золотое сечение” в скульптуре
Аполлон БельведерскийСамая знаменитая из них была
статуя Зевса Олимпийского, которая
считалась одним из чудес света.
42. статуя Афины Парфенос
43. “Золотое сечение” в изобразительном искусстве.
44. φ в архитектуре
Принцип «золотого» сечения применяетсяи архитектуре ,
причем независимо от века и страны .
Исследования показали:
эту волшебную пропорцию использовали и
строители пирамид в Египте,
и греческие архитекторы,
и русские зодчие,
и современные строительные организации.
45.
6238
46.
38Парфенон
47.
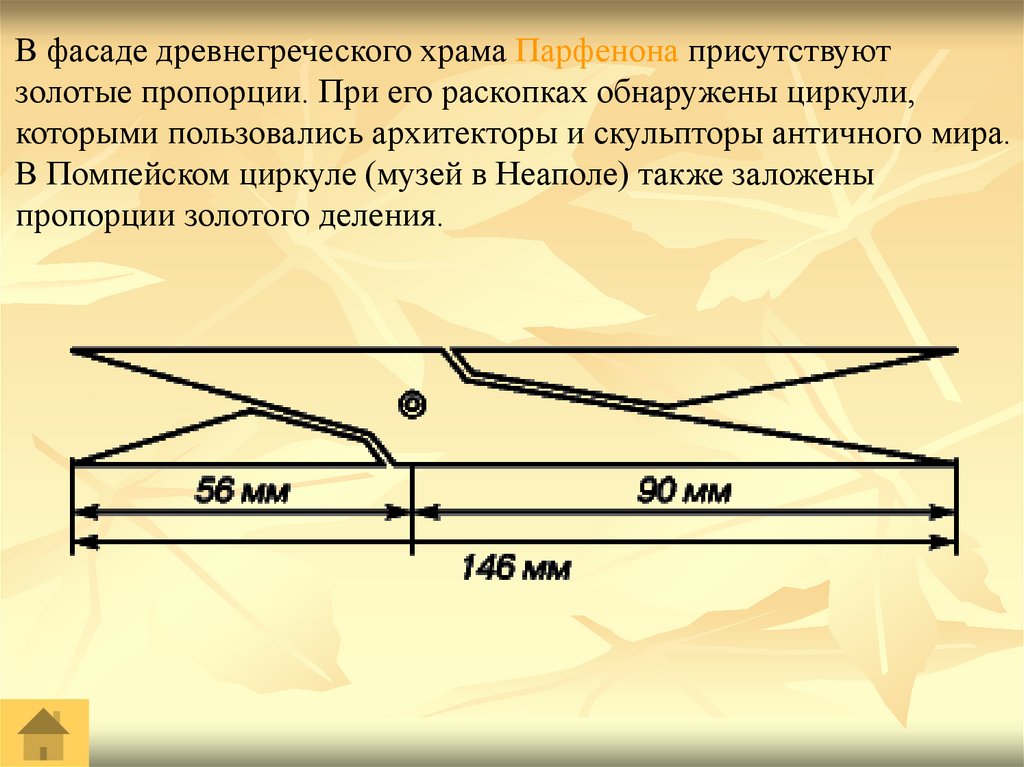
В фасаде древнегреческого храма Парфенона присутствуютзолотые пропорции. При его раскопках обнаружены циркули,
которыми пользовались архитекторы и скульпторы античного мира.
В Помпейском циркуле (музей в Неаполе) также заложены
пропорции золотого деления.
48. Есть в математике нечто вызывающее восторг Хаусдорф Ф.
Сфинкс, охраняющий гробницу ТутанхамонаПирамида Хеопса
Есть предположение, что
Пифагор понятие золотого
сечения позаимствовал у
египтян и вавилонян. И,
действительно пропорции
пирамиды Хеопса, барельефы
предметов быта и украшений
из гробницы Тутанхамона
свидетельствуют, что
египетские мастера
пользовались соотношением
золотого сечения при их
создании.
49. М.Ф. Казаков. 1738-1802 гг.
Известный русский архитекторКазаков Матвей Федорович в
своем творчестве широко
использовал “золотое сечение”.
Его талант был многогранным, но
в большей степени он раскрылся в
многочисленных осуществленных
проектах жилых домов и усадеб.
Например золотое сечение можно
обнаружить в архитектуре здания
Сената в Кремле. По проекту
Казакова построена в Москве
Голицынская больница, которая в
настоящее время называется
“Первая клиническая” больница
имени Пирогова.
50. Москва. Голицынская больница. 1794-1801 гг.
Здание Сената. Кремль.1776-1778 гг.
51. Петровский дворец в Москве 1776-1796 гг.
Построен по проекту М.Ф. Казакова.52. Собор Василия Блаженного .Москва.
53. «…, но, быть может, ещё лучше было бы назвать такой собор «окаменелой математикой» Юнг Д.
Пропорции Покровского Собора на Красной площади в Москве1; d ; d 2 ;...; d 7 .
определяются восемью членами ряда золотого сечения:
Многие члены этого ряда повторяются в затейливых элементах храма
d d 2 1; d 2 d 3 d ; d 3 d 4 d 2 ; и т.д.
многократно:
54. Церковь Вознесения в селе Коломенском (ныне Москва), 1532 г. Один из первых шатровых храмов на Руси.
55. «Гёте удачно назвал благородный собор «окаменелой музыкой», …» Юнг Д.
Церковь Покрова Богородицы на Нерли 1165«Простая» красота пропорций золотого сечения.
56.
АдмиралтействоДом – Пашкова.
В.И. Баженов.
57.
Золотое сечение в музыке и литературе.Многочисленные исследования
показали,
что в точке золотого сечения обычно
бывает кульминация поэтических ,
драматургических и музыкальных
произведений.
Золотое сечение мы находим в общей
композиции произведения и в отношении
его частей.
58. Золотое сечение в музыке.
Вначале 20 столетия на одном из заседаний московскогонаучно-музыкального кружка выступил Э. Розинов с докладом
«Закон золотого сечения в поэзии и музыке». Он
проанализировал популярные любимые музыкальные
произведения таких авторов, как Бах, Моцарт, Бетховен, Шопен,
Вагнер, Глинка, а также произведения народного творчества
наиболее древнего происхождения, и доказал ,что в них
существует золотое сечение.
Это произведения: Моцарта «Дон-Жуан»,
Бетховена «Лунная соната», «Руслан и Людмила» Глинки.
Мы можем сказать, что золотое сечение занимает особое
место в музыкальном произведении, это его кульминация,
особый подъем, особое возвышенное звучание.
Золотое сечение не может быть не в начале, ни в конце
произведения: до кульминации идет «знакомство» с
произведением, после кульминации - ощущается некий спад,
остается чувство завершенности, элементы обдумывания
услышанного.
59.
60.
ШопенМоцарт
61. Золотое сечение в литературе
Если рассмотреть понятие золотого сечения в литературе, томожем увидеть интересные факты. Остановимся на жизни и
творчестве Льва Николаевича Толстого(1828-1904).
Зная, что кульминация(пик, подъем в творчестве) приходится
на 36-48 лет , увидим, что знаменитую «Войну и мир» Толстой
создавал с 1863 по 1868 годы, то есть когда ему было 39-45 лет.
Да и женился писатель в 1862 году, когда ему исполнилось 38
лет. Огромная , сложная работа над романом - это исследование
собственной жизни, жизни человека и писателя. «Война и мир»это великий путь. Охватывающий жизнь России с 1805 по 1825
годы. Когда Россия, действительно переживала значимые
события(война 1812 года, восстание декабристов 1825), это тоже
своего рода золотое сечение в эпоху правления Александра
Первого.
62. «Если бы мне пришлось начать вновь своё обучение то я последовал бы совету Платона и принялся бы сперва за математику». Галилей
Г.По Платону: пять правильных
многогранников – пять стихий.
Додекаэдр олицетворяет
вселенную.
Платон считал додекаэдр самым
«правильным» из всех
правильных многогранников,
т. к. его грани – правильные
пятиугольники – сотканы из
золотых пропорций.
63. «Мышление начинается с удивления» Приписывается Аристотелю
Рисунки Леонардо да Винчииз книги Луки Пачоли «Божественная пропорция»
Леонардо да Винчи
любил мастерить
каркасы правильных
тел и преподносить
их в дар знатным
особам, возможно
пытаясь таким
образом приобщить
сильных мира сего к
философским
размышлениям о
красоте вечных
истин.
64. Да, путь познания не гладок, Но знаем мы со школьных лет: Загадок больше, чем разгадок, И поискам предела нет! Татьяничева Л.
Бог – отец «оберегает» вселенную, имеющую форму додекаэдра.12 граней додекаэдра и 12 апостолов Христа не просто
совпадение - в картине Сальвадора Дали «Тайная вечеря»
заключён глубокий религиозный смысл.
65. «Кто любит учиться - никогда не проводит время в праздности» Монтескье Ш
ВС
Золотой
прямоугольник
А
1
СD
1,6
AD
D
5 1
2
Многие современные изделия с прямоугольными гранями
имеют форму граней, близкую к «золотому сечению».
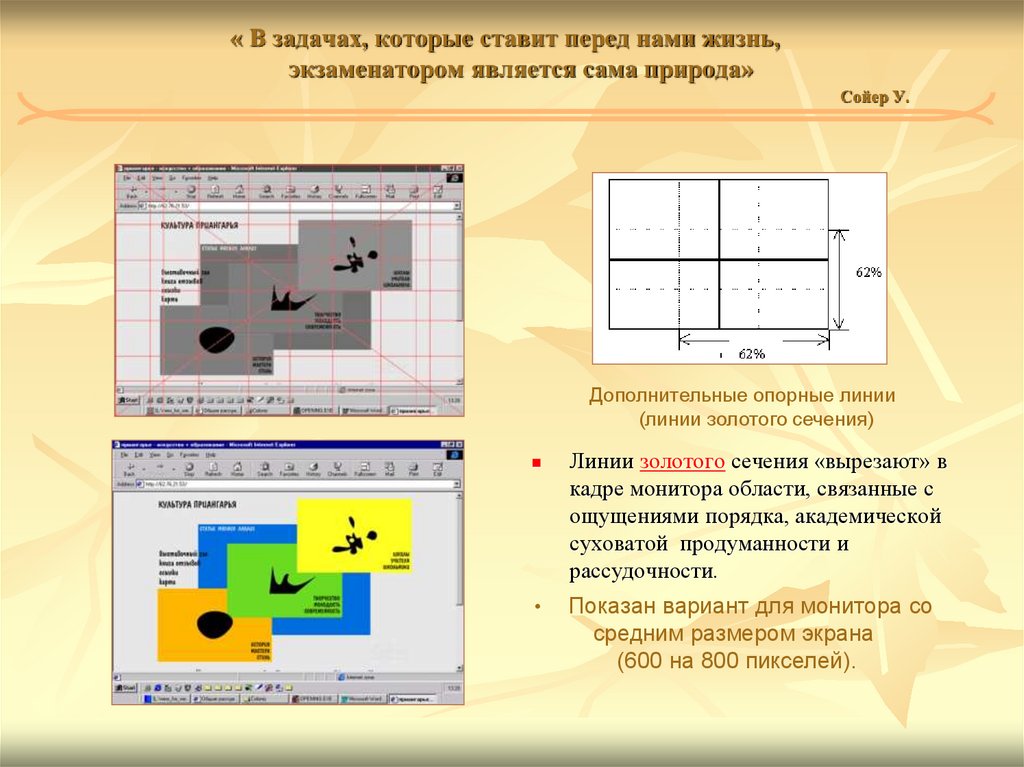
66. « В задачах, которые ставит перед нами жизнь, экзаменатором является сама природа» Сойер У.
Дополнительные опорные линии(линии золотого сечения)
Линии золотого сечения «вырезают» в
кадре монитора области, связанные с
ощущениями порядка, академической
суховатой продуманности и
рассудочности.
Показан вариант для монитора со
средним размером экрана
(600 на 800 пикселей).
67.
Решая квадратное уравнение мы открылиформулу красоты, показали почему именно такая
формула , где она применяется , как мы можем ее
использовать в нашей жизни .
Но при этом надо помнить , что можно открыть
законы внешней красоты , но внутреннюю
красоту измерить нельзя . Нет меры для
определения души человека .
68. Список используемой литературы
1.2.
3.
4.
А.В. Волошинов. Пифагор.- М: Просвещение, 1993 г.
Г.И. Глейзер. История математики в школе VII-VIII кл. Пособие
для учителей.- М: Просвещение, 1982 г.
www photoline.ru/tcomp 1.htm.
http//www.nips.riss-telecom.ru/poly/































































 mathematics
mathematics








