Similar presentations:
Урок по теории вероятности
1.
Урок по теориивероятности
© Варнек Татьяна Викторовна, учитель математики,
МОУ «СОШ №18» с углубленным изучением предметов,
Саратов, 2015
2.
Содержание• Классическое определение вероятности
• Теоремы сложения и умножения
вероятностей, формула Бернулли
• Таблицы вариантов, полный граф, дерево
вариантов
• Комбинаторика в вероятностных задачах
• Самостоятельная работа
3.
Классическое определениевероятности
Случайные события – те, исход которых
нельзя предугадать заранее
Равновозможные события – те, которые
в результате опыта не имеют бóльшую
возможность появления, чем другие
Пример: в урне лежит три шара – чёрный, белый,
синий. Однократные изъятия шаров любого цвета
– случайные равновозможные события.
4.
ОбозначениеВероятность случайного события А (Р(А))
– отношение числа благоприятствующих
ему событий (m) к общему число всех
элементарных событий (n)
Р(А) = m/n
5.
Схема решения1. Определить случайный эксперимент и его
исходы. Убедиться, что они
равновозможные.
2. Найти общее число событий N
3. Найти число благоприятствующих событий
искомому событию А (N(A))
4. Найти вероятность по формуле
Р(А) = N(A)/N
6.
ПримерКакова вероятность выпадения нечётной
цифры при бросании игральной кости?
Решение: пусть А – событие выпадения
нечётной цифры. Всего элементарных
событий n = 6 (т. к. 6 граней кубика);
благоприятствующих событий m = 3 (цифры 1,
3, 5). По формуле Р(А) = m/n = 3/6 = 0.5
Ответ: 0.5
7.
Сложение и умножениевероятностей
Событие называют противоположным
событию А, если оно происходит только
тогда, когда не происходит событие А и
обозначается Ā.
Сумма вероятностей противоположных событий равна 1
Р(А) + Р(Ā) = 1
8.
Два события называютсянесовместными, если в
одном и том же
испытании они не могут
произойти одновременно
9.
Теорема о сумме вероятностейЕсли событие С означает, что наступает
одно из двух несовместных событий А
или В, то вероятность событий С равна
сумме вероятностей событий А и В:
Р(С) = Р(А) + Р(В)
10.
Теорема о произведениивероятностей
Если событие С означает совместное
наступление двух независимых событий А и
В, то вероятность события С равна
произведению вероятностей событий А и В:
Р(С) = Р(А) * Р(В)
11.
ПримерВ коробке 19 шаров: 10 белых, 4 чёрные и 5 синих.
Из коробки наугад вынимают шар. Какова вероятность, что он окажется
не белым?
Решение: пусть событие А – шар оказался чёрным;
событие В – шар оказался синим;
событие С – вынутый шар не белый.
Тогда по формуле
Р(C ) Р( А) Р( В)
находим
4
5
9
Р( А) ; Р( В) Р(С ) .
19
19
19
Ответ:
9
Р (С ) .
19
12.
ПримерВ одном ящике 15 деталей, из которых 2 детали – нестандартные,
а в другом ящике – 20 деталей, из которых 3 нестандартные. Из
каждого ящика вынимают наугад по одной детали. Какова вероятность,
что обе детали окажутся нестандартными?
Решение: пусть событие А – из первого ящика вынули нестандартную
деталь; событие В – из второго ящика вынули нестандартную деталь.
Для события А - 15 исходов, 2 из которых благоприятные, а для
события В – 20 исходов, 3 из которых благоприятные, значит
2
3
Р(C ) Р( А) Р( В) Р ( А) , Р( В ) ;
15
20
Ответ: Р(С)=0,02
13.
Формула БернуллиПрименяется для вычисления k успехов в
серии из n попыток
k k n-k
n
P(A) = C p q
C
k
- число сочетаний
n
p – вероятность успеха
q = 1 - p – вероятность неудачи
14.
ПримерПри подбрасывании монеты (p =
q = 0.5), формула Бернулли
примет вид:
k
n
n
C
P(A) =
2
15.
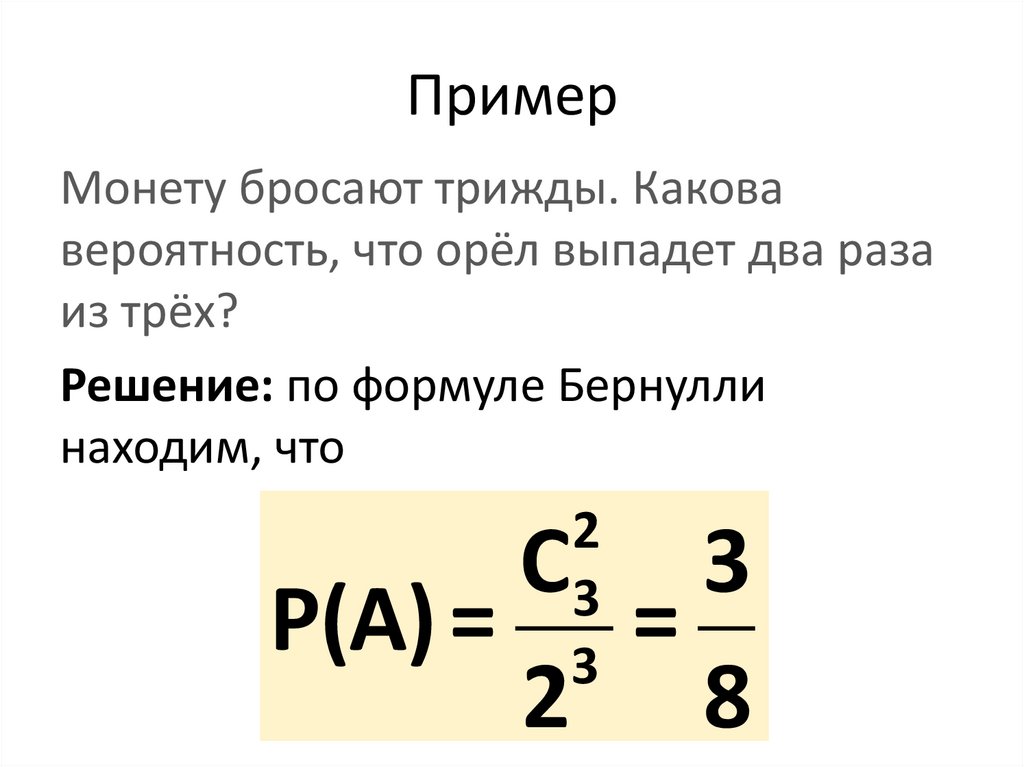
ПримерМонету бросают трижды. Какова
вероятность, что орёл выпадет два раза
из трёх?
Решение: по формуле Бернулли
находим, что
2
3
3
C 3
P(A) = =
2 8
16.
Таблицы вариантовДля решения комбинаторных задач
существуют различные средства,
исключающие возможность потери
какой-либо комбинации элементов.
Для подсчёта числа комбинаций из
двух элементов таким средство
является таблица вариантов
17.
ПримерЗаписать все возможные двузначные числа,
используя при этом цифры: 1) 1, 2 и 3; 2) 0, 1,
2 и 3. Подсчитать их количество N.
Ответ: 1) 9; 2) 12
18.
Правило произведенияЕсли существует n вариантов выбора
первого элемента и для каждого из них
есть m вариантов выбора второго
элемента, то всего существует n*m
различных пар с выбранными первым и
вторым элементами.
19.
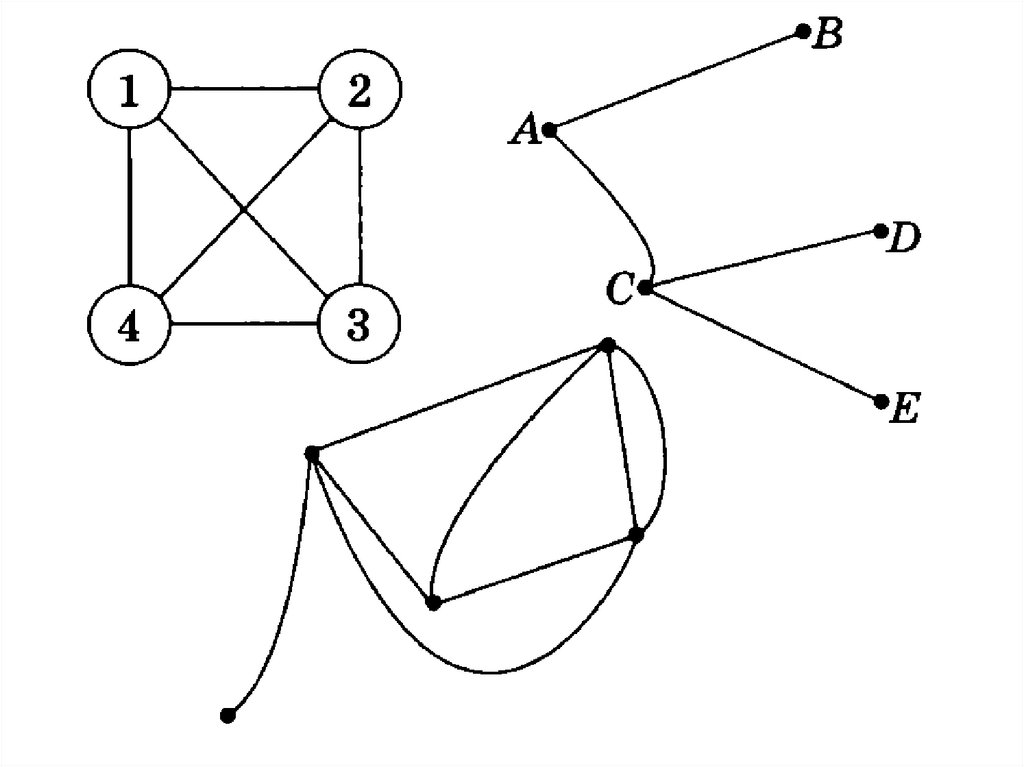
ГрафыНередко подсчёт вариантов облегчают графы. Так
называют геометрические фигуры, состоящие из
точек (вершин) и соединяющих их отрезков (рёбер).
При этом с помощью вершин изображают элементы
некоторого множества (предметов, людей,
числовых и буквенных кодов и т. п.), а с помощью
рёбер – определённые связи между этими
элементами. Для удобства иллюстрации условия
задачи с помощью графа его вершины-точки могут
быть заменены, например, кругами или
прямоугольниками, а рёбра-отрезки – любыми
линиями.
20.
21.
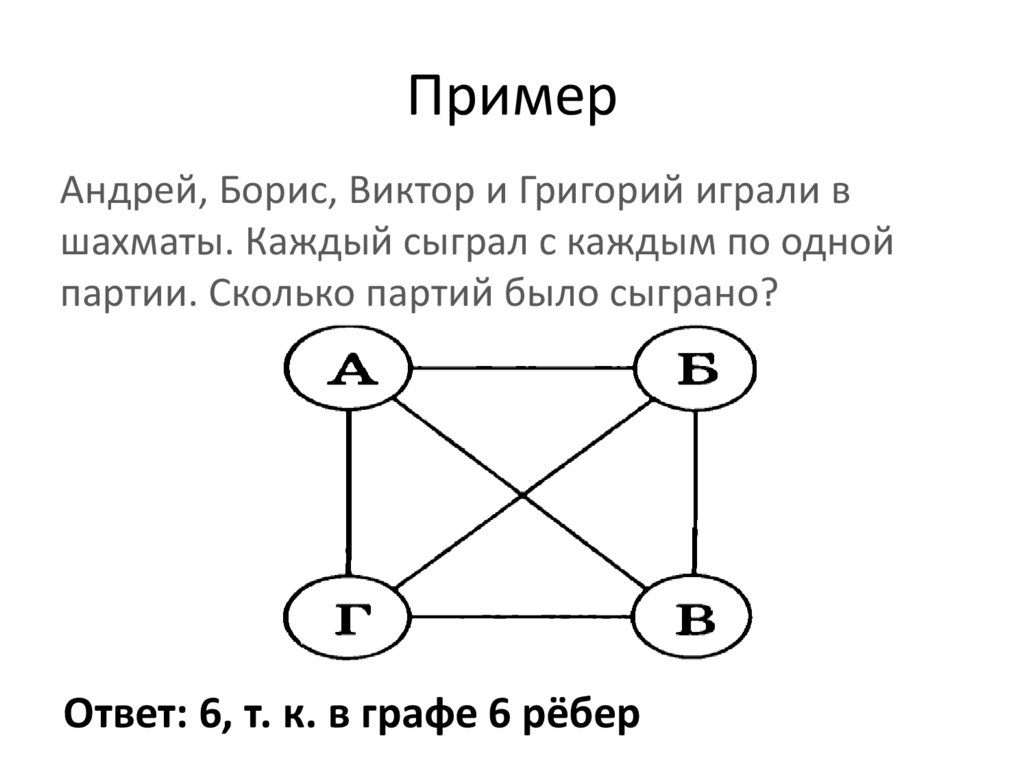
ПримерАндрей, Борис, Виктор и Григорий играли в
шахматы. Каждый сыграл с каждым по одной
партии. Сколько партий было сыграно?
Ответ: 6, т. к. в графе 6 рёбер
22.
Дерево вариантовГрафы такого вида называют деревом
вариантов. Вычерчивать дерево
полезно, когда требуется записать все
существующие комбинации из более,
чем 2 элементов. Дерево вариантов даёт
наглядное представление о том, как
применяется правило произведения.
23.
24.
Комбинаторика в решениивероятностных задач
Перестановки из n элементов –
комбинации n элементов, отличающиеся
друг от друга только порядком
расположения элементов.
Размещением из n элементов по k (k≤n) –
любое множество, состоящее из k
элементов, взятых в определённом
порядке из данных n элементов.
25.
перестановкаPn = n!
размещение
n!
A =
(n-k)!
k
n
26.
ПримерУчащиеся 2 класса изучают 9
предметов. Сколькими
способами можно составить
расписание на один день,
чтобы в нём было 4
различных предмета?
27.
Решение: любое расписание на один день,составленное из 4 (k) различных предметов,
отличается от любого другого набором
предметов, либо порядком их следования.
Значит, в этом примере речь идёт о
размещениях из 9 (n) элементов по 4 (k).
n!
A =
(n-k)!
k
n
по формуле размещения
9!
A =
= 6×7×8×9 = 3024
(9 - 4)!
4
9
28.
СочетаниеСочетанием из n элементов по k
называется любое множество,
составленное из k элементов,
выбранных из данных n элементов в
любом порядке.
n!
C =
k!(n-k)!
k
n
29.
ПримерИз набора, состоящего из 15
красок, надо выбрать 3 краски
для окрашивания шкатулки.
Сколькими способами можно
сделать этот выбор?
30.
Решение: каждый выбор трёх красокотличается от другого хотя бы одной краской.
Значит, здесь речь идёт о сочетаниях из 15
элементов по 3
n!
C =
k!(n-k)!
k
n
по формуле сочетания
15!
13×14×15
C =
=
= 455
3!(15 - 3)!
1×2×3
3
15
31.
Самостоятельная работаI вариант
1. Монету бросают дважды.
Какова вероятность, что орел
выпадет оба раза?
2. В конкурсе участвуют 20
человек: 8 из России, 7 из США,
остальные — из Китая. Какова
вероятность, что первая
участница окажется из Китая?
3. Из 1000 насосов подтекают
пять. Какова вероятность, что
один случайный насос не
подтекает?
II вариант
1. Игральную кость бросают
дважды. Какова вероятность,
что 6 не выпадет ни разу?
2. В соревнованиях участвуют 4
человека из России, 7 из
Дании, 9 из Швеции и 5 — из
США. Какова вероятность, что
последним выступит Швед?
3. На 100 сумок приходится
восемь бракованных. Какова
вероятность, что купленная
сумка окажется качественной.
Результат округлите до сотых.
32.
Самостоятельная работаI вариант
4. В кармане 4 монеты по
рублю и 2 монеты по 2 рубля.
Не глядя, переложили какие-то
три монеты в другой карман.
Какова вероятность, что
двухрублёвые монеты теперь
лежат в одном кармане?
5. Стоят два автомата. Каждый
из них может быть неисправен
с вероятностью 0,05
независимо от другого. Какова
вероятность, что хотя бы один
автомат исправен?
II вариант
4. В кармане 2 монеты по 5
рублей и 4 по 10 рублей. Не
глядя, переложили какие-то
три монеты в другой карман.
Какова вероятность, что
пятирублёвые монеты теперь
лежат в разных карманах?
5. Работает фонарь с двумя
лампами. Вероятность
перегорания лампы в течение
года равна 0,3. Какова
вероятность, что в течение
года хотя бы одна лампа не
перегорит?




























 mathematics
mathematics








