Общая классификация порядков роста

1.

Общая классификация порядков
роста
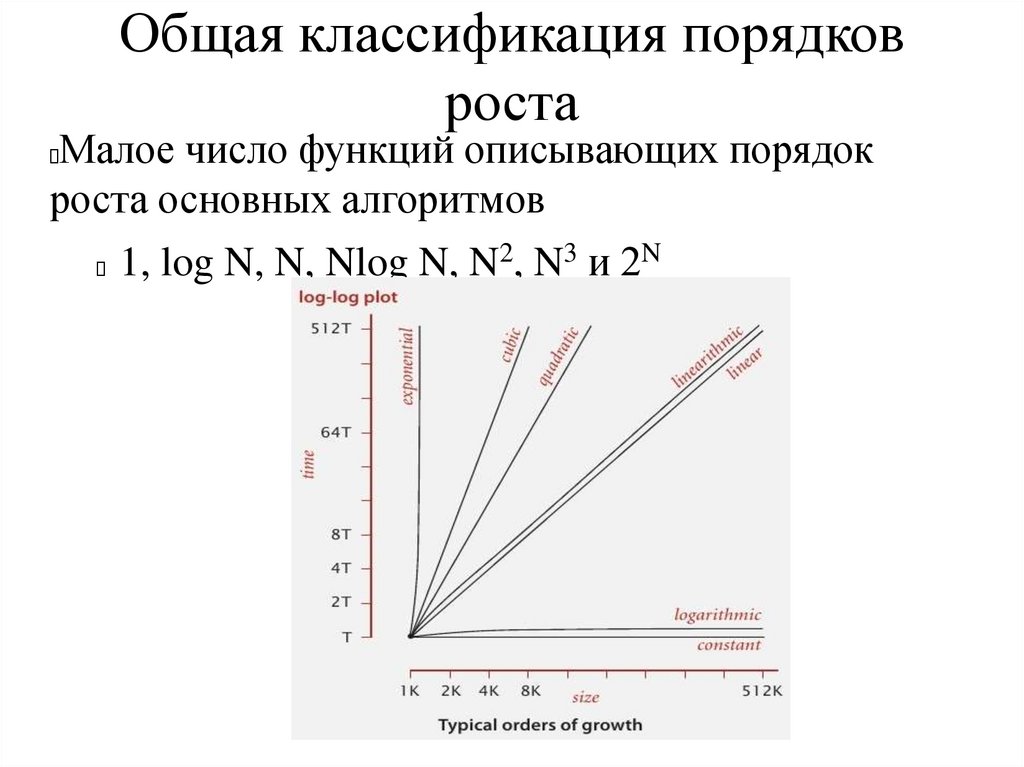
Малое число функций описывающих порядок
роста основных алгоритмов
1, log N, N, Nlog N, N2, N3 и 2N

2.

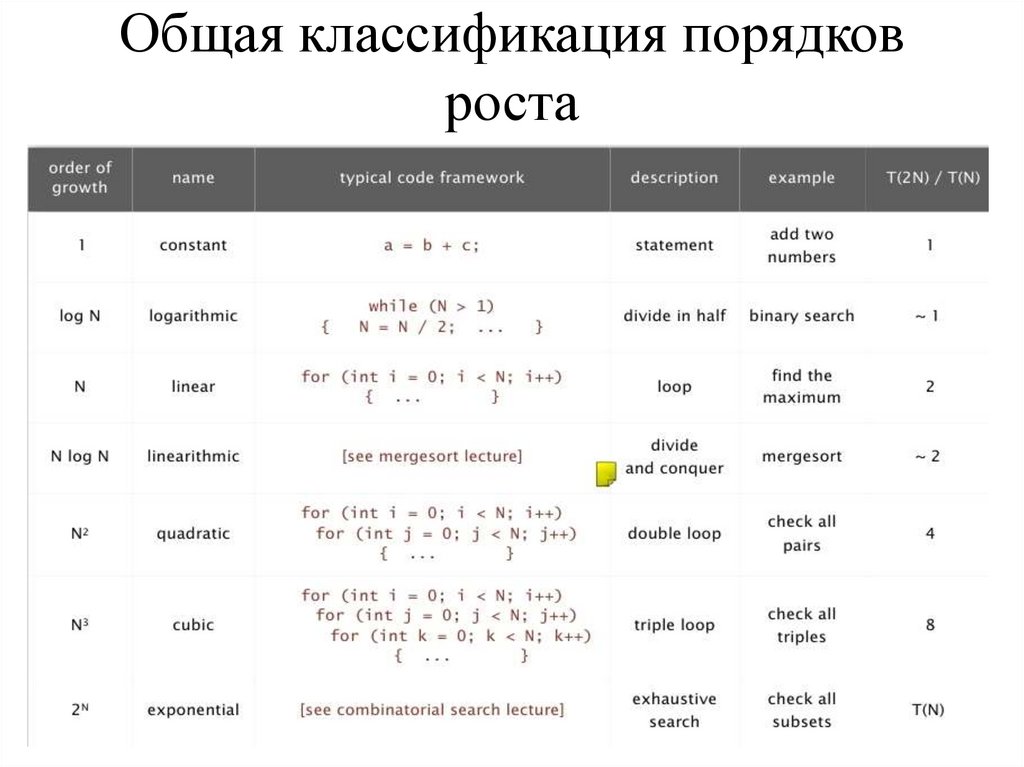
Общая классификация порядков
роста

3.

Практическое применение порядков
роста
Нижняя оценка. Нужны линейные или линейно-

4.

Бинарный поиск
Цель. Найти индекс ключа в отсортированном
массиве
Бинарный поиск
Ключ меньше — идем влево
Ключ больше — идем вправо
Равен — возвращаем результат

5.

Бинарный поиск: реализация
Впервые бинарный поиск был опубликован в 1946;
первая безошибочная реализация в 1962
Ошибка в Java.binarySearch() найдена в 2006

6.

Сортировка выбором
На итерации i найти минимальный оставшийся
элемент с индексом min
Поменять местами a[i] и a[min]
Видео 1

7.

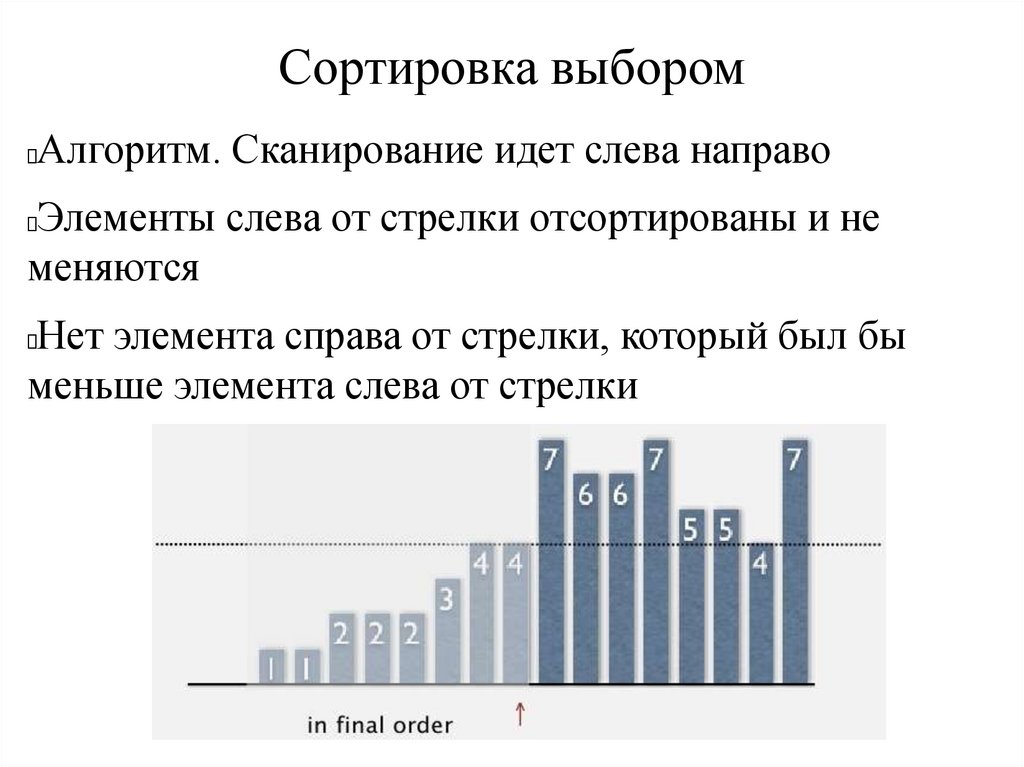
Сортировка выбором
Алгоритм. Сканирование идет слева направо
Элементы слева от стрелки отсортированы и не
меняются
Нет элемента справа от стрелки, который был бы
меньше элемента слева от стрелки

8.

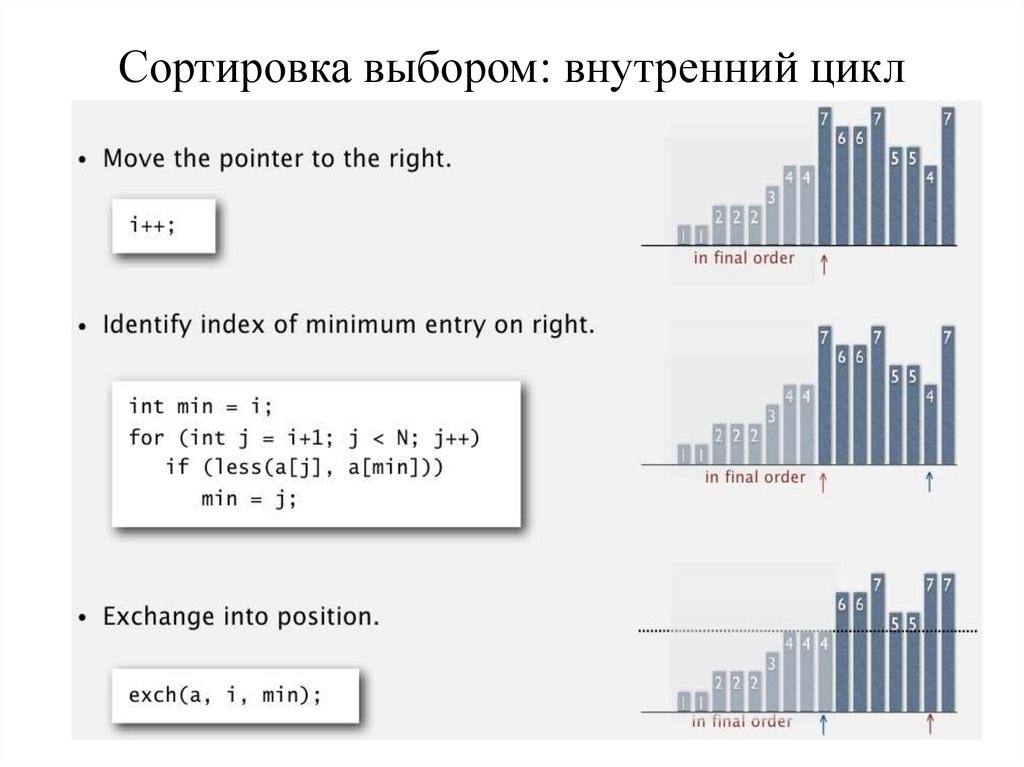
Сортировка выбором: внутренний цикл

9.

Сортировка выбором: реализация на Java

10.

Сортировка выбором:
математический анализ
Утверждение. Сортировка выбором использует (N1) + (N-2) + … + 1 + 0 ~ N2/2 сравнений и N
перестановок
Время выполнения не зависит от входных данных.
Квадратичное время, даже если массив

11.

Видео 2

12.

Сортировка вставками

13.

Сортировка вставками
На итерации i поменять a[i] с каждым большим
элементом слева
Видео 3

14.

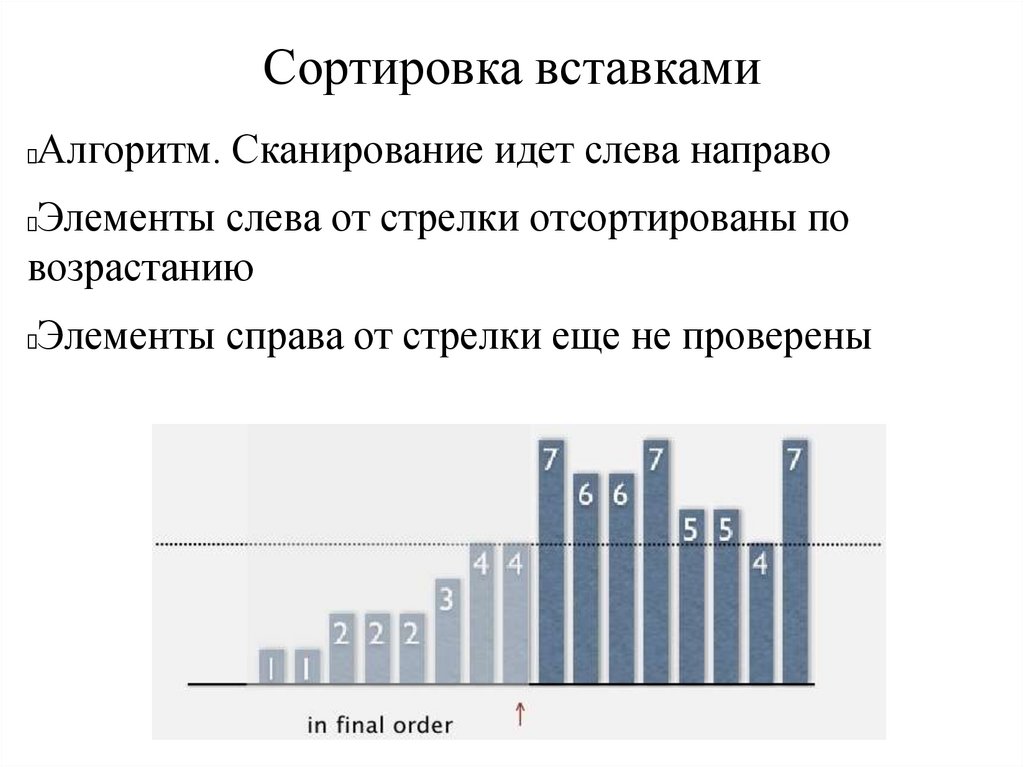
Сортировка вставками
Алгоритм. Сканирование идет слева направо
Элементы слева от стрелки отсортированы по
возрастанию
Элементы справа от стрелки еще не проверены

15.

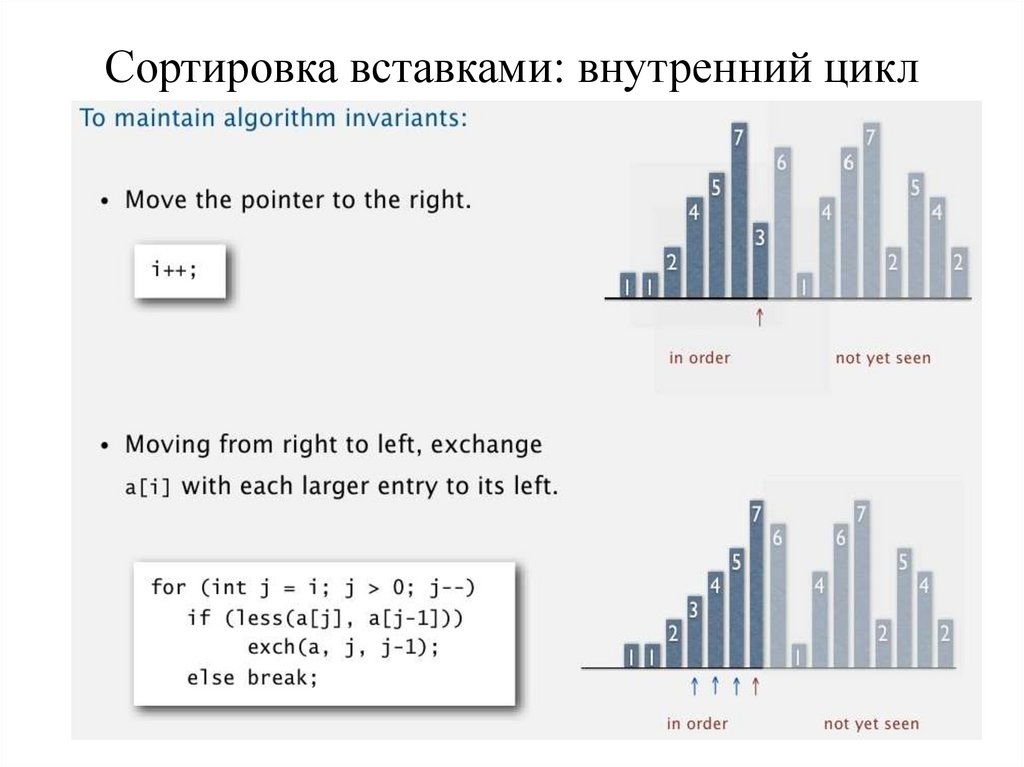
Сортировка вставками: внутренний цикл

16.

Сортировка вставками: реализация на Java

17.

Сортировка вставками:
математический анализ
Утверждение. Сортировка вставками использует ~
N2/4 сравнений и ~ N2/4 перестановок при
случайном наборе данных
В среднем каждый ключ проходит половину пути

18.

Сортировка вставками: пример

19.

Видео 4

20.

Сортировка вставками: лучший и
худший случай
Лучший случай. Массив отсортирован; необходимо
N-1 сравнений и 0 перестановок
AEELMOPRSTX
Худший случай. Массив отсортирован в обратно
порядке и нет дубликатов; ~ N2/2 сравнений и ~
N2/2 вставок
XTS R PO M LE EA

21.

Видео 5

22.

Сортировка вставками: частично
упорядоченный массив
Инверсия — пара элементов, которая нарушает
упорядоченность в массиве
Частично упорядоченный массив — массив, в
котором количество инверсий <= cN
Массив, каждый элемент которого находится
неподалеку от своей окончательной позиции
Небольшой массив, добавленный к большому
отсортированному массиву

23.

Видео 6