Вычислимость: разрешимые и перечислимые языки. Лекция 12

1. Вычислимость: разрешимые и перечислимые языки

2.

Определение распознавательной задачи:
имеется
множество
объектов
определенное подмножество
и
требуется
найти эффективную процедуру (т.е. алгоритм), с
помощью которой для любого
можно
определить
или
.
При
этом
распознавательная
задача
называется алгоритмически разрешимой или
алгоритмически неразрешимой в зависимости от
того, имеется или нет алгоритм решения этой
задачи.

3.

Конструктивные объекты любого множества
можно кодировать словами конечного множества
(например, состоящего из двоичных символов 0 и 1) с
помощью взаимно-однозначного отображения
,
где
- множество всех слов над алфавитом .
В
результате
распознавательная
задача
формулируется следующим универсальным образом:
имеется множество слов
над некоторым
алфавитом и определенный язык
требуется
найти эффективную процедуру (т.е. алгоритм), с
помощью которой для любого слова
можно
определить
или
.

4.

Определение 1. Язык L называется разрешимым
(или рекурсивным), если существует такая машина
Тьюринга T, что для любого слова
выполняются
условия:
1) если
, то при входе w машина T попадает в
заключительное состояние, останавливается и выдает
значение
2) если
, то при входе w машина T попадает в
заключительное состояние, останавливается и выдает
значение
Такие машины соответствуют понятию «алгоритма»
и применяются при решении распознавательных задач
типа «да/нет».

5.

Множество всех разрешимых языков будем
обозначать R (от Recursive)
Свойства: дополнения, конечные пересечения
и конечные объединения разрешимых языков
являются разрешимыми языками.

6.

Примеры разрешимых языков.
• Пустой язык;
• Множество всех строк;
• Конечные множества;
• Множество четных чисел;
• Множество простых чисел;
• Множество рациональных чисел,
меньших числа е;
• Множество n, при которых в числе
есть п девяток подряд.

7.

Определение
2.
Язык
L
называется
полуразрешимым
или
перечислимым,
если
существует такая машина Тьюринга T, что
,
т.е. при входе
машина T попадает в
заключительное состояние, останавливается и
выдает значение
, а при входе
машина
Тьюринга T не дает никакого результата.
Множество всех полуразрешимых языков будем
обозначать RE (от Recursive Enumerable).

8.

Лемма. Существуют неразрешимые языки,
поскольку алгоритмов счетное число, а языков
несчетное.
Аналогично можно доказать, что существуют
языки, не являющиеся полуразрешимыми.
Основная
теорема.
Существуют
полуразрешимые неразрешимые языки, т.е.
полуразрешимые языки, которые не могут быть
разрешимы никаким алгоритмом, т.е. выполняется
свойство R RE.

9.

Классификация
распознавательных
задач
определяется классификацией кодирующих эти
задачи языков.
Определение
называется
3.
Распознавательная
разрешимой
задача
(соответственно,
полуразрешимой), если разрешим (соответственно,
полуразрешим) кодирующий эту задачу язык.

10.

Главные примеры.
1.
Распознавательная
задача
ВЫП
(SАТ)
выполнимости формулы алгебры высказываний
разрешима (с помощью алгоритма составления
истинностных таблиц).
2. Распознавательная задача ТЕОРЕМА (THM)
доказуемости
формулы
полуразрешима
(с
алгебры
помощью
формул), но не разрешима.
предикатов
понятия
вывода

11. Сложность вычислений

12.

В качестве модели алгоритма рассматривается
машина Тьюринга T, вычисляющая числовую функцию
Временной сложностью машины T называется
функция
значение которой равно числу шагов
работы машины T, сделанных при вычислении значения
если
определено, и
не определено, если
не определено.
Ленточной сложностью машины T называется
функция
значение которой равно числу ячеек
машины T, используемых при вычислении значения
и
не определено, если
не определено.

13.

Говорят, что машина Тьюринга T
полиномиальную временную сложность
имеет
k
=n
(или «время работы ограничено полиномом
»),
если, обрабатывая вход
более
длины п, T делает не
переходов и останавливается независимо
от того, допущен вход или нет.
Определение. Говорят, что язык
классу
P,
если
он
разрешим
принадлежит
некоторой
детерминированной машины Тьюринга
полиномиальной временной сложностью.
T
с

14.

Определение.
Распознавательная
задача
принадлежит классу P, если ее язык принадлежит
классу P, т.е. эта задача решается с помощью
полиномиального
алгоритма
детерминированной
машины
-
некоторой
Тьюринга
T
с
полиномиальной временной сложностью.
Пример. Задача вычисления НОД целых чисел
принадлежит классу P.

15.

Помимо детерминированной машины Тьюринга
Т=( ,Q, , q , q ) с одной программой
S
F
в теории
алгоритмов рассматриваются недетерминированные
машины
Тьюринга
программами
Т=( ,Q, 1, 2, q , q )
S
F
с
двумя
1, 2, которая на каждом шаге
вычислений случайным образом выбирает одну из
этих двух программ и по ней выполняет изменение
своей конфигурации.

16.

Определение. Язык
принадлежит классу NP,
если
он
разрешим
некоторой
недетерминированной машины Тьюринга T с
полиномиальной временной сложностью.
Определение.
Распознавательная
задача
принадлежит классу NP, если ее язык
принадлежит классу NP, т.е. эта задача решается с
помощью
полиномиального
недетерминированного алгоритма - некоторой
недетерминированной машины Тьюринга T с
полиномиальной временной сложностью.

17.

Это равносильно тому, что для объектов задачи x
имеется полиноминально ограниченный эталон y, с
помощью которого за полиномиальное время
проверяется, что x является или нет решением данной
задачи.
Главный пример. Распознавательная задача ВЫП
(SАТ)
выполнимости
формулы
алгебры
высказываний принадлежит классу NP.
Очевидно, что P NP, но вопрос о равенстве этих
классов является важной открытой проблемой.

18. Полиномиальные сведения

19.

Основной метод доказательства того, что проблему
P2 нельзя решить за полиномиальное время (т.е.
P2 P ) состоит в сведении к ней за полиномиальное
время такой проблемы P1, что P1 P . Такое
преобразование языков называется полиномиальным
сведением.
Определение. Говорят, что язык
является NPтрудным, если для любого языка
из класса NP
существует полиномиальное сведение языка
к
языку

20.

Определение. Говорят, что язык является NPполным, если он принадлежит классу NP и
является NP-трудным.
Теорема 1. Если проблема P1 является NPтрудной и существует полиномиальное сведение
проблемы P1 к проблеме P2 , то проблема P2
также NP-трудна.
Следствие. Если проблема P1 является NPполной и существует полиномиальное сведение
проблемы P1 к проблеме P2 NP , то проблема P2
также NP-полна.

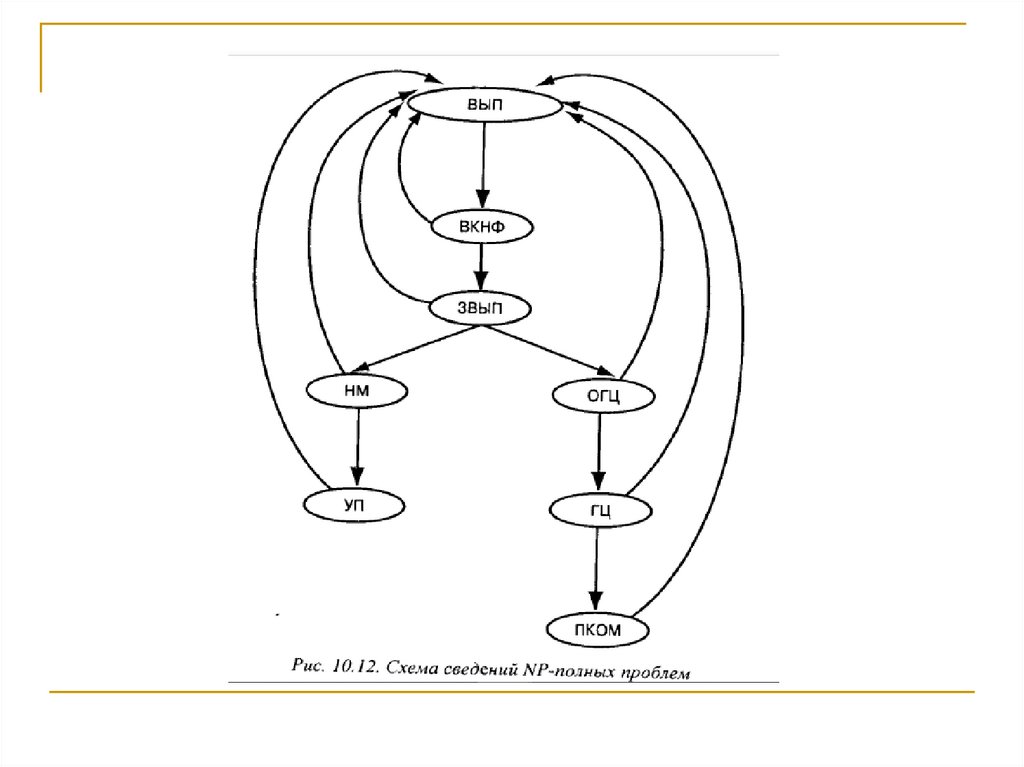
21. Основные NP-полные проблемы

22.

Форма описания NP-полной проблемы:
Название проблемы и ее аббревиатура.
2. Вход проблемы: что и каким образом
представляют данные.
3. Искомый выход: при каких условиях
выходом будет «да».
4. Известная проблема, сведение которой
к данной проблеме доказывает NP1.
полноту последней.

23.

Проблема выполнимости (ВЫП)
Формулы алгебры высказываний строятся из
следующих элементов.
1. Пропозициональные переменные, принимающие
значения 1 (истина) или 0 (ложь).
2. Бинарные
операторы
, ,
обозначающие
логические связки И, ИЛИ двух формул.
3. Унарный оператор , который обозначает
логическое отрицание.
4. Скобки для группирования операторов и
операндов, если необходимо изменить порядок
старшинства
(приоритетов)
операторов,
принятый по умолчанию (вначале применяется , затем и, наконец, ).

24.

Представление экземпляров ВЫП
Используется следующий код.
1. Символы , , , и скобки (,) представляют
самих себя.
2.Переменная Xi представляется символом X с
дописанной к нему последовательностью нулей
и единиц — двоичной записью числа i.
Таким образом, алфавит A проблемы-языка ВЫП
содержит всего восемь символов. Все экземпляры
ВЫП являются цепочками символов - словами в
этом фиксированном конечном алфавите.

25.

Проблема выполнимости (ВЫП)
Вход: слова w в алфавите A, кодирующие
формулы алгебры
экземпляры ВЫП.
высказываний
-
Выход: значение 1 - ответ «да» - тогда и
только тогда, когда закодированная
формула
выполнима.
алгебры
высказываний

26.

Проблема выполнимости (ВЫП) формул
алгебры высказываний состоит в следующем
выяснить,
выполнима
ли
данная
формула алгебры высказываний ?
Теорема Кука. Проблема ВЫП NP-полна.

27.

Проблема выполнимости (ВКНФ)
Проблема выполнимости ВКНФ
формул
алгебры высказываний состоит в следующем
выяснить, выполнима ли данная формула
алгебры высказываний в форме КНФ?

28.

Вход проблемы ВКНФ:
слова w в алфавите A, кодирующие формулы
алгебры высказываний форме КНФ экземпляры ВКНФ.
Искомый выход:
значение 1 - ответ «да» - тогда и только
тогда, когда закодированная формула
алгебры высказываний выполнима.
Известная NP-полная проблема, которая
сводится к ВКНФ – проблема ВЫП.

29.

Теорема. Для любой формулы алгебры логики за
полиномиальное время можно построить такую
формулу алгебры логики в форме КНФ, что
выполняются условия:
1) формула выполнима в том и только том
случае, если выполнима КНФ ;
2) длина формулы линейно зависит от
количества символов в формуле .
Доказательство: индукцией по числу символов
операций в формуле проносим отрицания к
переменным и затем индукцией по длине формулы
получаем формулу в форме КНФ.

30.

Теорема. Проблема ВЫП полиномиально
сводится к проблеме ВКНФ.
Следствие. Проблема ВКНФ NP-полная.

31.

Ограниченная проблема выполнимости (3ВЫП)
Ограниченная проблема выполнимости 3ВЫП формул алгебры высказываний состоит в
следующем
выяснить, выполнима ли данная формула
алгебры высказываний в форме КНФ с
дизъюнктами из 3 литер?

32.

Вход проблемы 3-ВЫП:
слова w в алфавите A, кодирующие формулы
алгебры высказываний в форме КНФ с
дизъюнктами из 3 литер - экземпляры ВКНФ.
Искомый выход:
значение 1 - ответ «да» - тогда и только
тогда, когда закодированная формула
выполнима.
Известная NP-полная проблема, которая
сводится к 3-ВЫП – проблема ВКНФ.

33.

Теорема. Для любой формулы алгебры высказываний
в форме КНФ за полиномиальное время можно
построить такую формулу алгебры высказываний в
форме КНФ с
дизъюнктами из 3 литер, что
выполняются условия:
1) формула выполнима в том и только том
случае, если выполнима КНФ ;
2) длина формулы линейно зависит от
количества символов в формуле .
Доказательство:
индукцией по числу символов
операций в дизъюнктах формулы
получаем
формулу в форме КНФ с дизъюнктами из 3 литер.

34.

Теорема. Проблема ВКНФ полиномиально
сводится к проблеме 3-ВЫП.
Следствие. Проблема 3-ВЫП NP-полная.

35.

36.

37.

Проблема независимого множества (НМ):
Вход: граф
и нижняя граница k,
удовлетворяющая условию
Выход: ответ «да» тогда и только тогда,
когда G имеет независимое множество из k
вершин.
Проблема, сводящаяся к данной: Проблема
3-ВЫП.
Следствие. Проблема НМ NP-полна.

38.

39.

Проблема вершинного покрытия (ВП):
Вход: граф
и нижняя граница k,
удовлетворяющая условию
Выход: ответ «да» тогда и только тогда, когда
G имеет вершинное покрытие из k или менее
числа вершин.
Проблема, сводящаяся к данной: Проблема
НМ.
Следствие. Проблема ВП NP-полна.

40.

Проблема ориентированного гамильтонова
цикла (ОГЦ):
Вход: ориентированный граф G.
Выход: ответ «да» тогда и только тогда,
когда
G
имеет
ориентированный
гамильтонов цикл.
Проблема,
сводящаяся
к
данной:
Проблема 3-ВЫП.
Следствие. Проблема ОГЦ NP-полна.

41.

Проблема гамильтонова цикла (ГЦ):
Вход: неориентированный граф G.
Выход: ответ «да» тогда и только тогда, когда
G имеет гамильтонов цикл.
Проблема, сводящаяся к данной: Проблема
ОГЦ.
Следствие. Проблема ГЦ NP-полна.

42.

Проблема коммивояжера (ПКОМ):
Вход: взвешенный граф G и предельное
значение k.
Выход: ответ «да» тогда и только тогда, когда
G имеет гамильтонов цикл веса не
превышающего k.
Проблема, сводящаяся к данной: Проблема
ГЦ.
Следствие. Проблема ПКОМ NP-полна.

43.

Задача целочисленного программирования
(ЗЦП):
Вход: система линейных ограничений,
целевая функция и предельное значение k.
Выход: ответ «да» тогда и только тогда, когда
функция имеет превышающее k значение для
допустимых переменных.
Проблема, сводящаяся к данной: Проблема
3-ВЫП.
Следствие. Проблема ЗЦП NP-полна.