Анализ алгоритмов. Причины для анализа алгоритмов

1.

Анализ алгоритмов

2.

3.

4.

Причины для анализа алгоритмов
Предсказание производительности
Сравнение алгоритмов
Предоставление гарантий
Понимание теоретических основ
Основная цель на практике: избежать ошибок
производительности (performance bugs)

5.

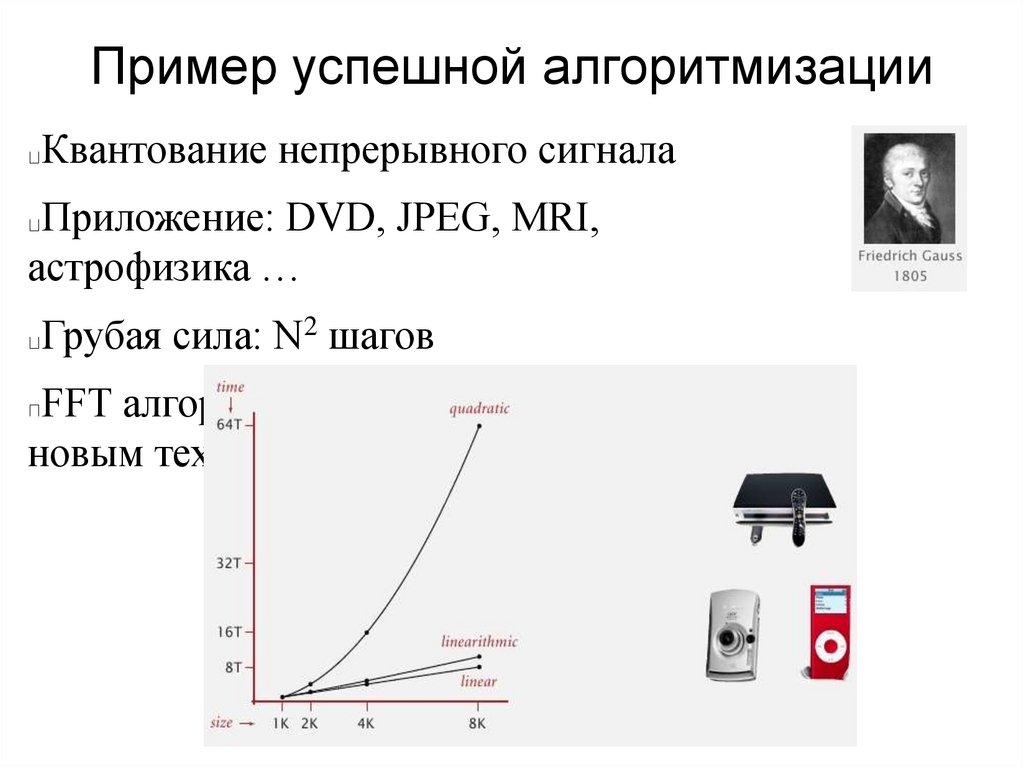
Пример успешной алгоритмизации
Квантование непрерывного сигнала
Приложение: DVD, JPEG, MRI,
астрофизика …
Грубая сила: N2 шагов
FFT алгоритм: N logN шагов (доступ к
новым технологиям)

6.

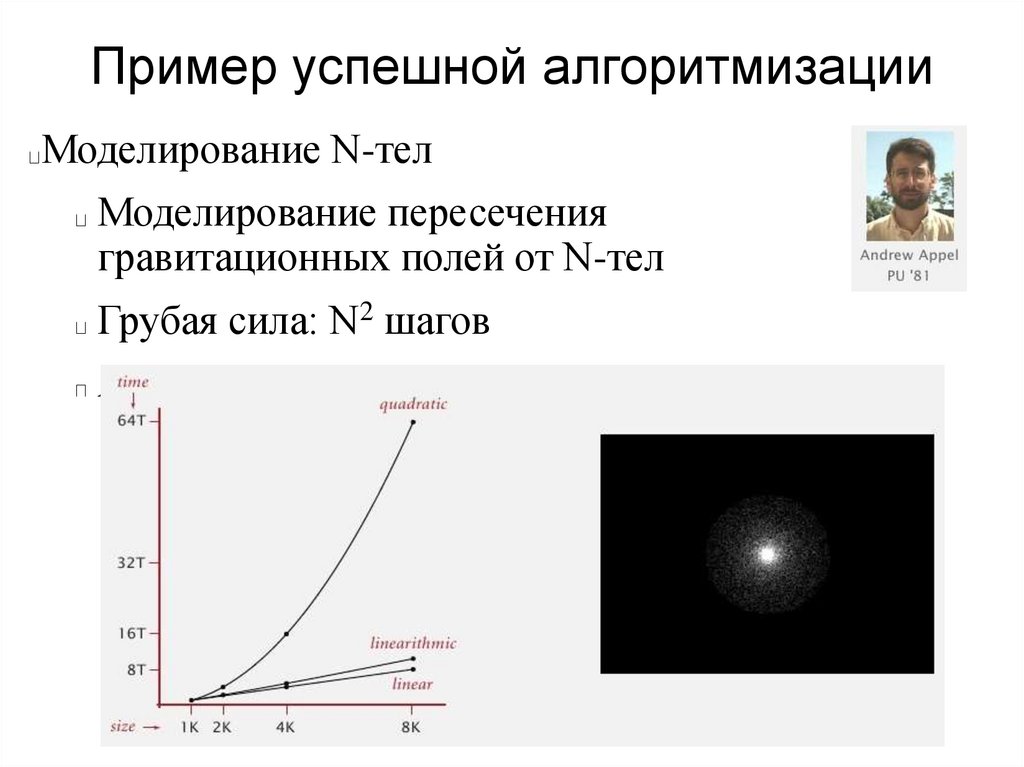
Пример успешной алгоритмизации
Моделирование N-тел
Моделирование пересечения
гравитационных полей от N-тел
Грубая сила: N2 шагов
Алгоритм Барнса-Хата: N logN шагов

7.

Вопрос
Решит ли моя программа задачу с большим
набором входных данных
Дональд Кнут (1970-е): Использование научного
метода для понимания производительности

8.

Применение научного метода для
понимания производительности
Научный метод
Наблюдение какого-либо явления
Выдвижение гипотезы, которая согласуется с
наблюдением
Предсказания явления с помощью гипотезы
Проверка предсказания с помощью наблюдения
Подтверждение с помощью повторений до тех
пор, пока гипотеза и наблюдение не согласуются
Принципы
Эксперимент должен быть воспроизводимым

9.

Наблюдение

10.

Пример: сумма троек
Сумма троек. Возьмем N целых чисел. Сколько
сумм трех чисел равно нулю?

11.

Сумма троек: метод грубой силы

12.

13.

14.

Эмпирический анализ
Запуск программы с различными входными
данными и измерение времени выполнения

15.

Анализ данных
Шкала с линейным масштабом

16.

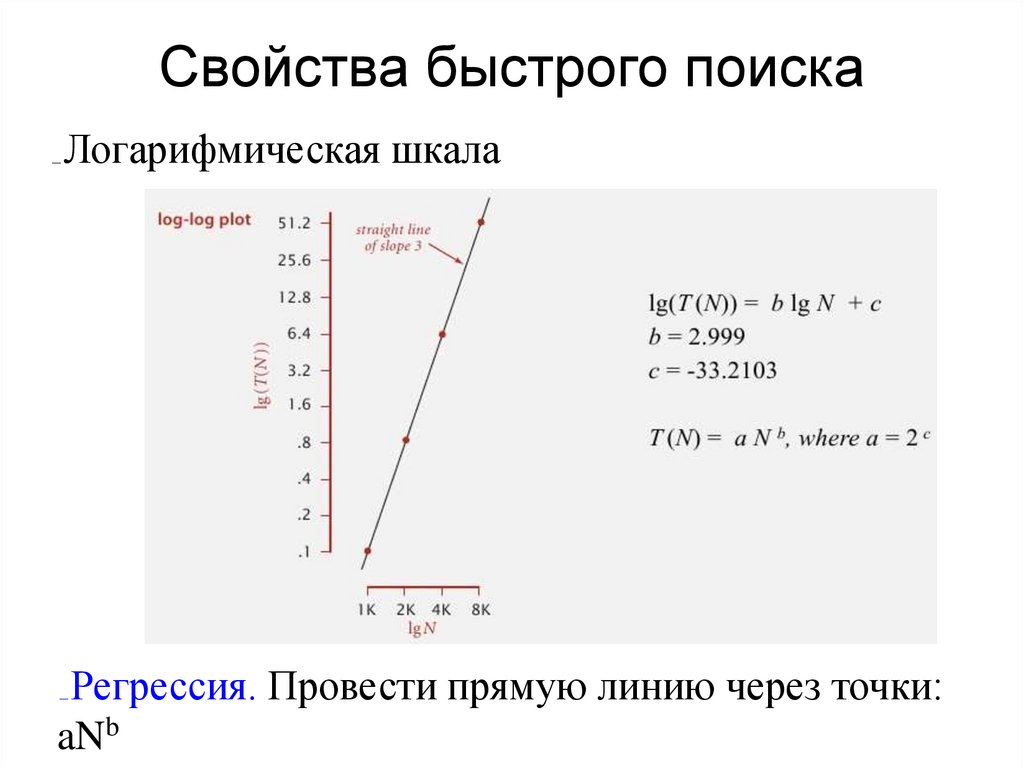
Свойства быстрого поиска
Логарифмическая шкала
Регрессия. Провести прямую линию через точки:
aNb

17.

Предсказание и проверка
Гипотеза. Время выполнения 1,006 * 10-10 * N2,999
секунд
Предсказание.
51,0 секунда для N = 8000
408,1 секунда для N = 16000
Наблюдение.

18.

Удвоение гипотезы
Запустить программу с удвоенным размером
входных данных
Гипотеза. Время выполнения aNb, где b = log2
(ratio)

19.

Удвоение гипотезы
Вопрос: Как оценить а (если мы знаем b)?
Ответ: Запустить программу (на большом наборе
данных N) и найти a.
Гипотеза. Время выполнения 0,998 * 10-10 * N3

20.

Экспериментальная алгоритмика

21.

Математические модели

22.

Математические модели для
времени выполнения
Общее время выполнения. Сумма: стоимость
каждой операции * частоту, для всех операций
Анализ программ нужно производить на
определенном наборе операций
Стоимость зависит от компьютера и
компилятора
Частота зависит от алгоритма и входных
данных
В принципе, создать точную математическую
модель возможно.

23.

Стоимость основных операций

24.

Стоимость основных операций
Ошибка новичков: неправильная оценка

25.

Пример: 1-Sum
Подсчет количества инструкций, как функции от
N.

26.

Пример: 2-Sum
Подсчет количества инструкций, как функции от
N.

27.

Упрощение вычислений

28.

Упрощение 1: модель стоимости
Модель стоимости. Использовать некоторые
основные операции для приближенного расчета
времени выполнения.

29.

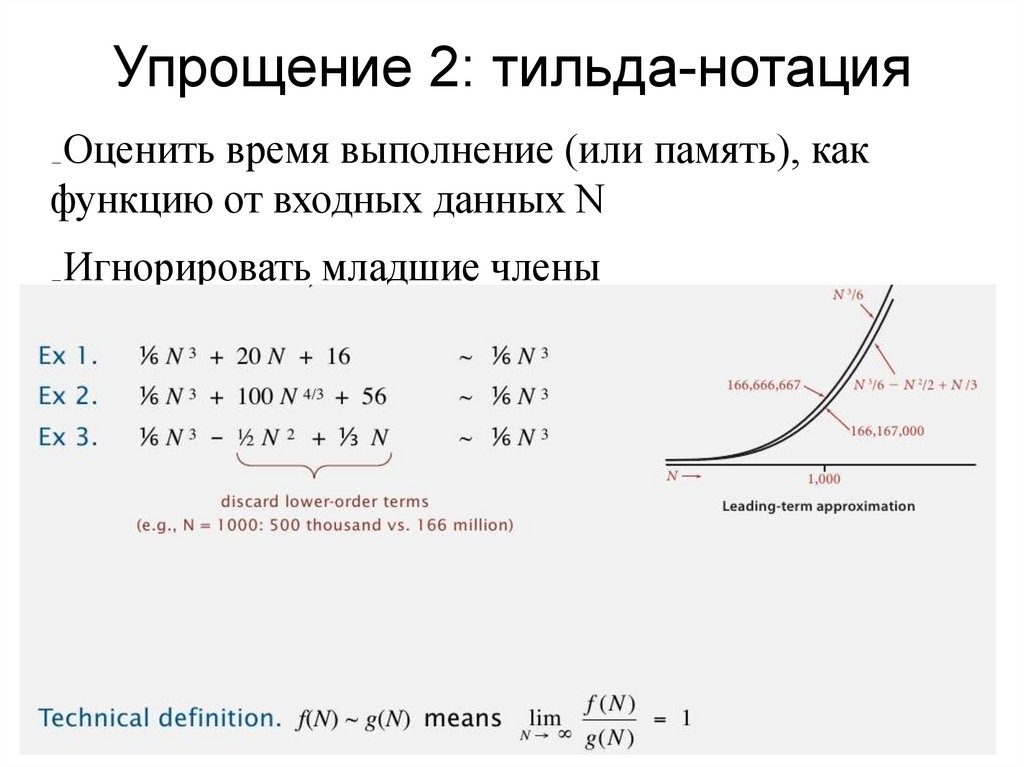
Упрощение 2: тильда-нотация
Оценить время выполнение (или память), как
функцию от входных данных N
Игнорировать младшие члены
Когда N велико, младшие члены незначительны
Когда N мало, мы не о чем не заботимся

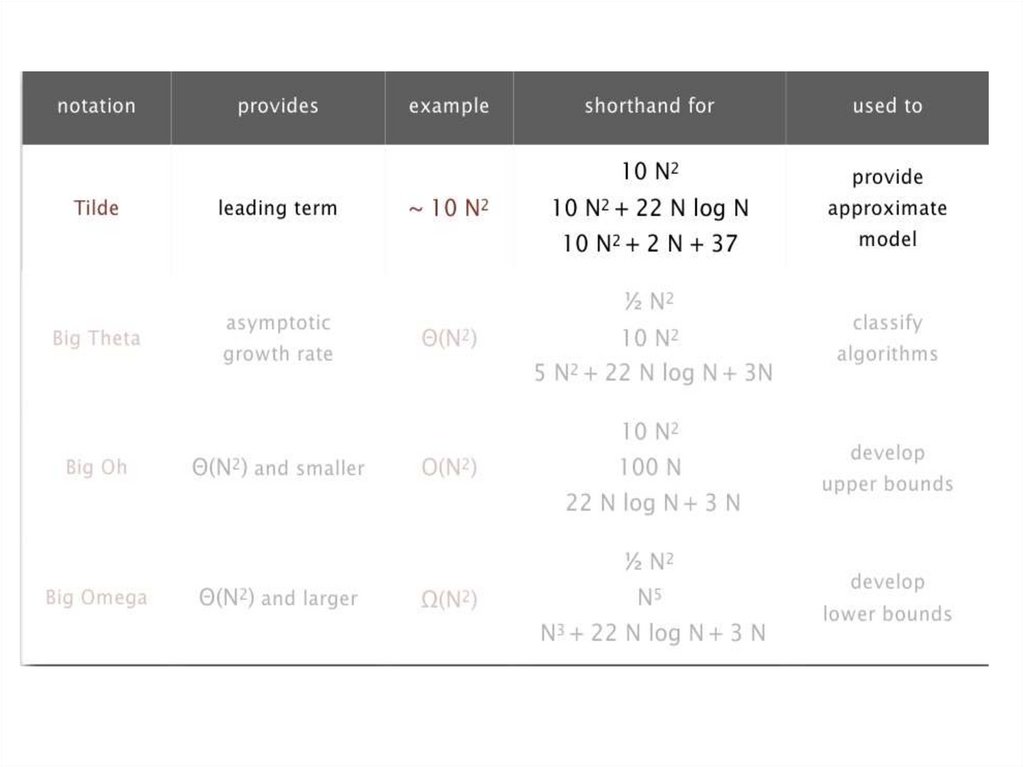
30.

Упрощение 2: тильда-нотация
Оценить время выполнение (или память), как
функцию от входных данных N
Игнорировать младшие члены
Когда N велико, младшие члены незначительны
Когда N мало, мы не о чем не заботимся

31.

Пример: 2-Sum
Нижняя оценка. Использовать модель стоимости и

32.

Пример: 3-Sum
Нижняя оценка. Использовать модель стоимости и

33.

Оценка дискретной суммы
Как оценить дискретную сумму?
1)Средствами дискретной математики.
2)Заменить сумму на определенный интеграл и
посчитать

34.

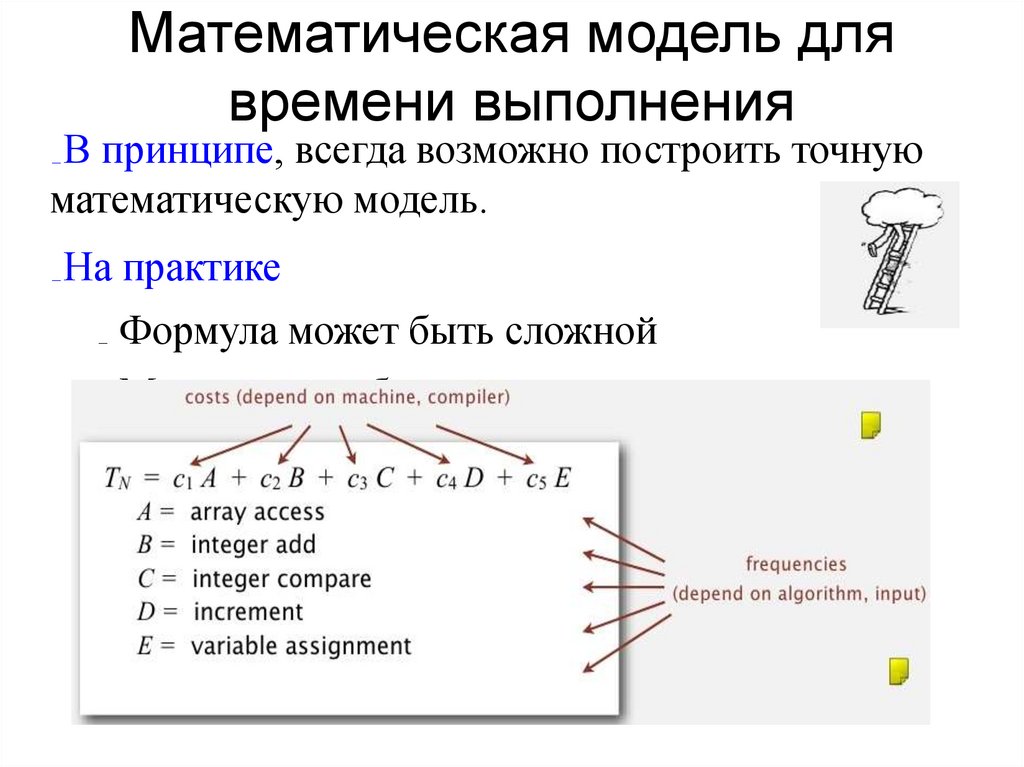
Математическая модель для
времени выполнения
В принципе, всегда возможно построить точную
математическую модель.
На практике
Формула может быть сложной
Могут понадобиться дополнительные
математические знания
Точные модели лучше оставить экспертам

35.

Классификация порядков роста

36.

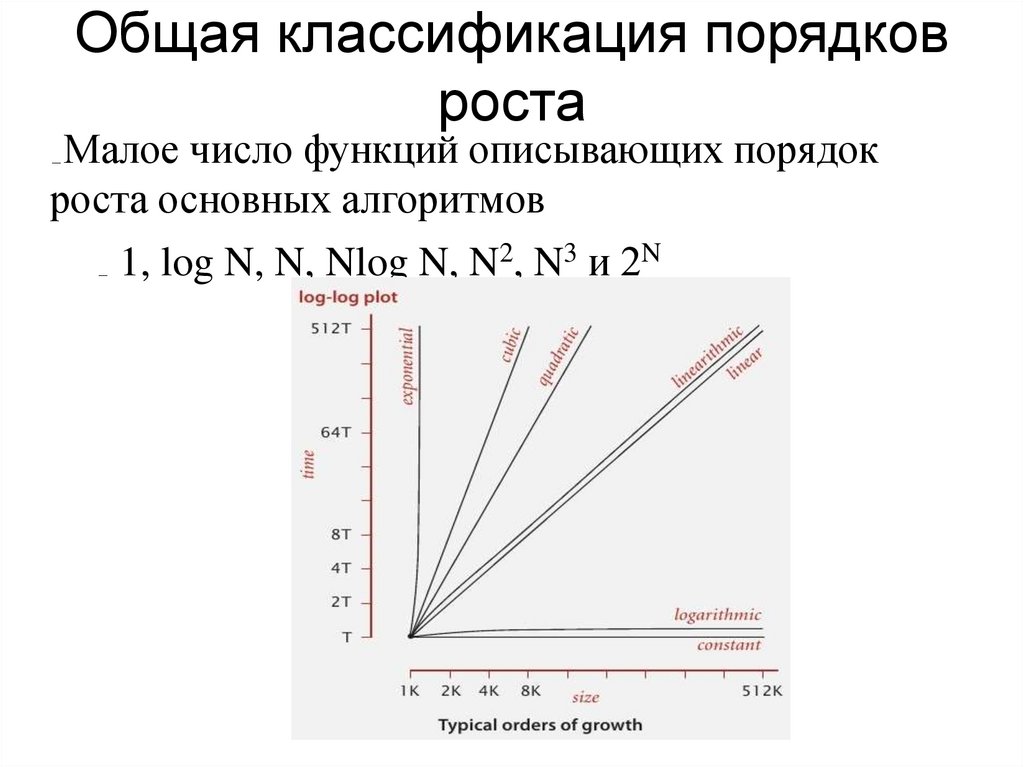
Общая классификация порядков
роста
Малое число функций описывающих порядок
роста основных алгоритмов
1, log N, N, Nlog N, N2, N3 и 2N

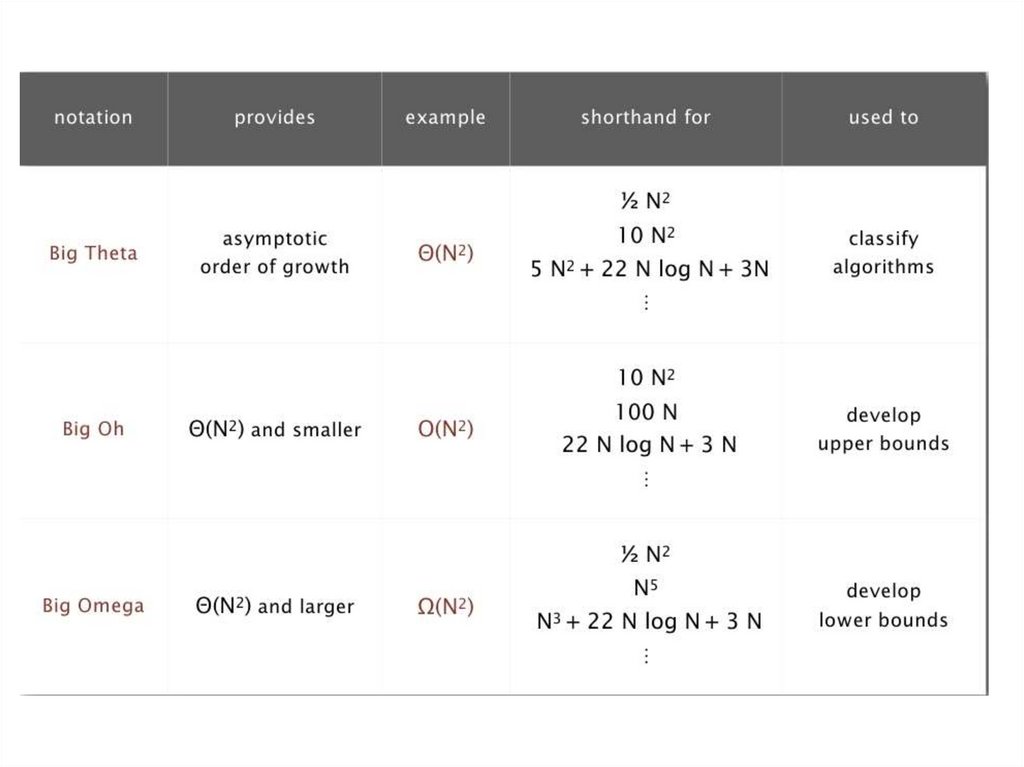
37.

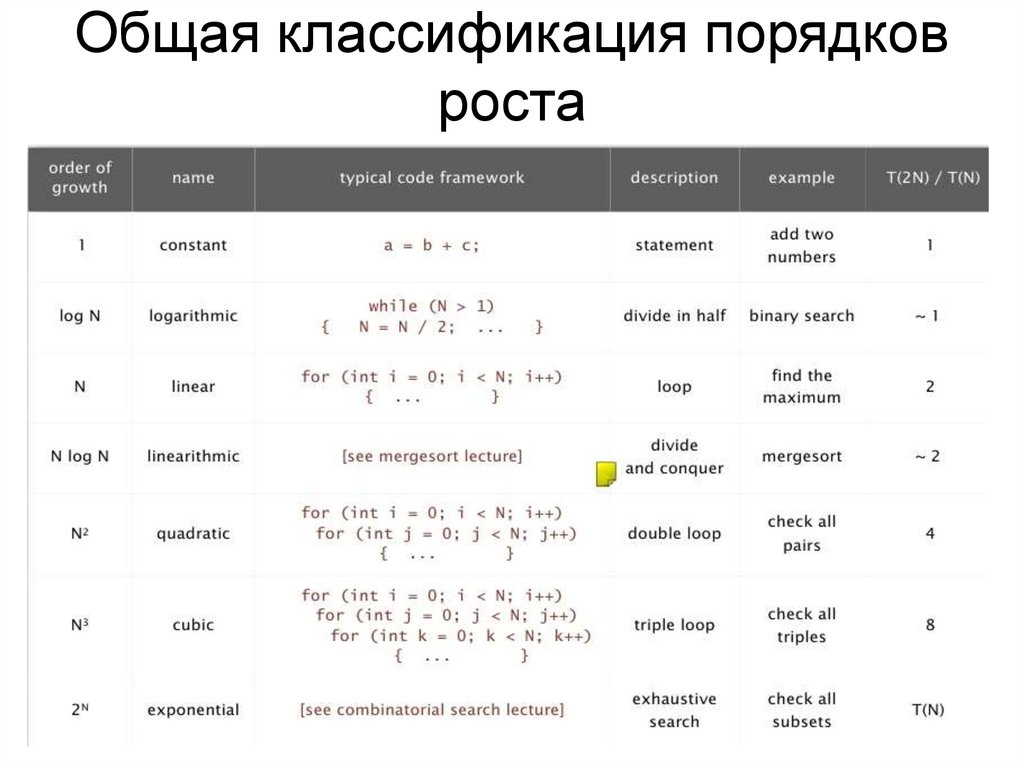
Общая классификация порядков
роста

38.

Практическое применение
порядков роста
Нижняя оценка. Нужны линейные или линейно-

39.

Бинарный поиск
Цель. Найти индекс ключа в отсортированном
массиве
Бинарный поиск
Ключ меньше — идем влево
Ключ больше — идем вправо
Равен — возвращаем результат

40.

Бинарный поиск: реализация
Впервые бинарный поиск был опубликован в 1946;
первая безошибочная реализация в 1962
Ошибка в Java.binarySearch() найдена в 2006

41.

Бинарный поиск: математический
анализ
Предположение. Бинарный поиск использует 1 + lg
N сравнений ключа в отсортированном массиве N
T(N) количество сравнений ключа в
отсортированном массиве размером <= N
T(N) <= T(N / 2) + 1, для N > 1, с T(1) = 1

42.

N2log N алгоритм для 3-Sum
Алгоритм основанный на
сортировке
Шаг 1: Сортировка N чисел
Шаг 2: Для каждой пары
чисел a[i] и a[j] сделать
бинарный поиск для -(a[i] +
a[j])
Анализ. Порядок роста N2log
N
Шаг 1: N2 сортировка
вставками
Шаг 2: N2log N бинарный

43.

Сравнение программ
Гипотеза. Основанный на сортировке 3-Sum
алгоритм N2log N однозначно быстрее метода
грубой силы N3
Главный принцип. Лучший порядок роста =>
быстрота на практике

44.

Теория алгоритмов

45.

Типы анализа
Лучший случай. Нижняя граница по стоимости
Определяется самыми «простыми» входными
данными
Цель для любых входных данных
Худший случай. Верхняя граница
Определяется «самыми сложными» входными
данными
Предоставляет гарантии для всех возможных
входных данных
Средний случай. Ожидаемая стоимость для
случайных входных данных

46.

Типы анализа
Лучший случай. Нижняя граница по стоимости
Худший случай. Верхняя граница
Средний случай. Ожидаемая стоимость для
случайных входных данных
Реальные входные данные могут не
соответствовать модели
Нужно понимать, что может быть на входе,
чтобы эффективно обрабатывать данные
Подход 1: строить модель для худшего случая
Подход 2: строить модель для случайных

47.

48.

Пример: два алгоритма
сортировки
Быстрая сортировка
Количество сравнений в худшем случае: N2
O(N2)
Сортировка слиянием
Количество сравнений в худшем случае: N logN
O(N logN)
Известно, что на практике быстрая сортировка в
два раза быстрее и использует в два раза меньше
памяти, чем сортировка слиянием.

49.

50.

Память

51.

Основы
Бит. 0 или 1
Байт. 8 бит
Мегабайт (MB). 1 миллион или 220 байт
Гигабайт (GB). 1 миллиард или 230 байт
64-битная машина
Может адресовать больше памяти
Указатели занимают больше места

52.

Использование памяти для
основных типов и массивов

53.

Использование памяти объектами
в Java
Заголовок объекта: 16 байт.
Указатели: 8 байт.
Дополнение блока данных: каждый объект кратен
8 байтам.
Пример. Объект, использующий 32 байта памяти

54.

Выводы
Эмпирический анализ
Запустить программу и засечь время выполнения
Определить порядок роста и сформулировать
гипотезу времени выполнения
Модель позволяет нам делать предсказания
Математический анализ
Подсчитать количество операций и частоту их
выполнения
Использовать тильда нотацию для упрощения
анализа
Модель позволяет нам предсказать поведение