Similar presentations:
Методика обучения учащихся профильных классов решению геометрических задач векторно-координатным методом
1.
ааМетодика обучения
учащихся профильных
классов решению
геометрических задач
векторнокоординатным
методом
Автор работы: Трунина Кристина Валериевна
НАУЧНЫЙ РУКОВОДИТЕЛЬ: Дербеденева Наталья
2.
АКТУАЛЬНОСТЬ ИССЛЕДОВАНИЯАКТУАЛЬНОСТЬ ОБУСЛОВЛЕНА нарастающей потребностью в разработке и
внедрении инновационных методов обучения математике, особенно в контексте
геометрии.
В современной практике ВОЗНИКАЕТ ПРОТИВОРЕЧИЕ между необходимостью
обучения
старшеклассников
умению
решать
геометрические
задачи
и
недостаточной сформированностью у них методов и приемов, среди которых
наибольшую трудность вызывают векторный и координатный методы.
3.
ЦЕЛЬ И ЗАДАЧИ ИССЛЕДОВАНИЯЦЕЛЬЮ ИССЛЕДОВАНИЯ стало разработка научно
обоснованной методики обучения учащихся старших классов
решению геометрических задач векторно-координатным
методом.
ЗАДАЧИ:
• ПРОВЕСТИ анализ научной и учебно-методической литературы по проблеме
исследования, изучить опыт учителей по применению векторно-координатного
метода к решению геометрических задач;
• ВЫЯВИТЬ теоретические основы применения векторно-координатного метода к
решению геометрических задач, определить цели и особенности обучения учащихся
профильных классов решению геометрических задач векторно-координатным
методом;
• ИЗУЧИТЬ различные методы решения геометрических задач, обосновать
преимущества векторно-координатного метода;
• ОБОСНОВАТЬ и РАЗРАБОТАТЬ методику обучения учащихся старших классов
решению геометрических задач векторно-координатным методом;
• ПРОВЕРИТЬ экспериментально эффективность использования разработанной
методики.
4.
ОБЪЕКТ И ПРЕДМЕТ ИССЛЕДОВАНИЯОБЪЕКТОМ ИССЛЕДОВАНИЯ является
процесс обучения геометрии в
общеобразовательной школе.
ПРЕДМЕТОМ ИССЛЕДОВАНИЯ является
методические особенности
применения векторно-координатного
метода решения геометрических задач
для учащихся старших классов.
5.
Значимость исследованияТЕОРЕТИЧЕСКАЯ ЗНАЧИМОСТЬ исследования
состоит в том, что раскрыта сущность методики
обучения решению задач векторно-координатным
методом на основе системы задач и элективного
курса.
Практическая
значимость
исследования
состоит в том, что его результаты могут быть
использованы
при
составлении
учебнометодических разработок для учителей математики
по изучению векторно-координатного метода и его
применению к решению геометрических задач, при
организации соответствующего элективного курса
для учащихся старших классов и непосредственно в
практике обучения геометрии.
6.
История векторно-координатного методаПьер Ферма
Рене
Декарт
Уильям
Гамильтон
7.
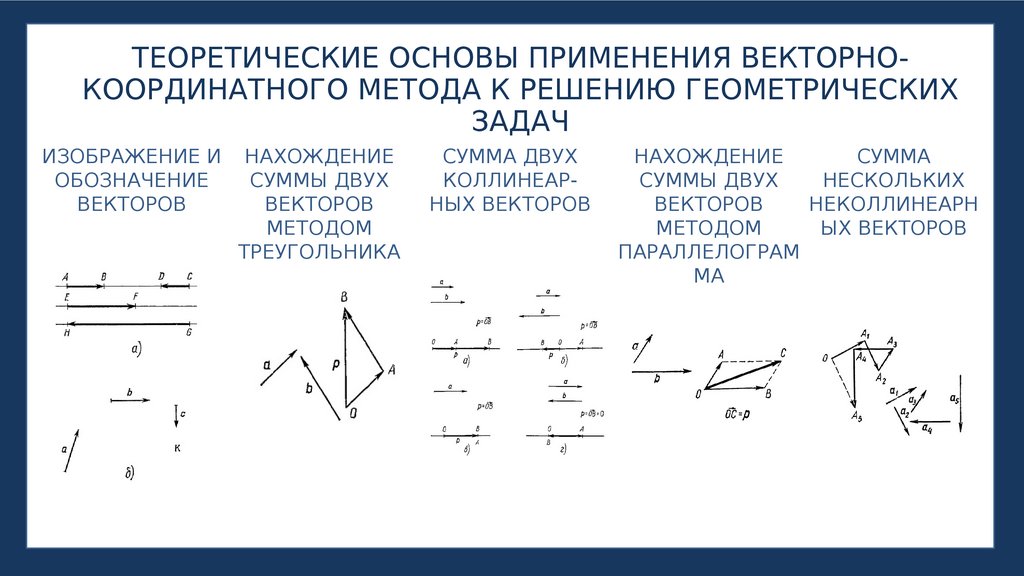
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХЗАДАЧ
ИЗОБРАЖЕНИЕ И
ОБОЗНАЧЕНИЕ
ВЕКТОРОВ
НАХОЖДЕНИЕ
СУММЫ ДВУХ
ВЕКТОРОВ
МЕТОДОМ
ТРЕУГОЛЬНИКА
СУММА ДВУХ
КОЛЛИНЕАРНЫХ ВЕКТОРОВ
НАХОЖДЕНИЕ
СУММА
СУММЫ ДВУХ
НЕСКОЛЬКИХ
ВЕКТОРОВ
НЕКОЛЛИНЕАРН
МЕТОДОМ
ЫХ ВЕКТОРОВ
ПАРАЛЛЕЛОГРАМ
МА
8.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХЗАДАЧ
ПО ХАРАКТЕРУ
ТРЕБОВАНИЙ В ТЕОРИИ И
МЕТОДИКЕ ОБУЧЕНИЯ
МАТЕМАТИКЕ ВЫДЕЛЯЮТ
ТОЛЬКО ПЯТЬ
РАЗЛИЧНЫХ ТИПОВ
ЗАДАЧ:
1) задачи на нахождение
искомых (вычисление);
2)
задачи
на
преобразование;
3)
задачи
на
доказательство;
4) задачи на построение;
5) задачи на объяснение.
АНАЛИЗ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ
ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРНОКООРДИНАТНОГО МЕТОДОВ
ВЫДЕЛЯЮТ ВИДЫ ЗАДАЧ:
1) задача на нахождение расстояния между
двумя точками;
2)
задача
на
нахождение
координат
середины отрезка;
3) задача на вычисление угла между двумя
векторами;
4) задача на вычисление угла между прямой
и плоскостью;
5) задача на вычисление угла между
плоскостями;
6) задача на нахождение расстояния от
произвольной точки до плоскости.
9.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХЗАДАЧ
Е.
И.
Лященко
описывает
следующими
словами
суть
координатного метода: «Это способ определения положения точки
(на прямой, на плоскости, в пространстве) с помощью чисел (для
декартовой системы координат). Используя координатный метод,
алгебраические
уравнения
можно
истолковать
в
виде
геометрических образов (графиков) и, наоборот, искать решение
геометрических задач с помощью аналитических формул (уравнений
и их систем)».
ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ЗНАНИЯМ, УМЕНИЯМ И
НАВЫКАМ УЧАЩИХСЯ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ
ВЕКТОРНО-КООРДИНАТНЫМ МЕТОДОМ:
ДАЮТ ОБОСНОВАНИЕ применения
графического или аналитического
языка в зависимости от конкретной
ситуации задачи;
УМЕЮТ наиболее рационально
разместить фигуру на координатной
плоскости для применения
координатного метода при решении
математической задачи»
10.
Анализ содержания темы в УМК по геометрииАвторы
учебника
Л. С. Атанасян
Класс, кол-во часов
Содержания векторно-координатного метода
10 класс, Глава 4. Векторы в 1) главенствующим методом решения задач является метод координат;
пространстве, 7 ч.
2) рассматриваются формулы для вычисления углов и расстояний;
11 класс, Глава 5.
3) выражение скалярного, векторного и смешанного произведения векторов в
Метод координат в пространстве, координатной форме.
15 ч.
Е. В. Потоскуев,
Л. И. Звавич
10 класс, Глава 6. Векторный 1) перевод условия геометрической задачи на «векторный язык»;
метод в пространстве, 10 ч.
2) безошибочное выполнение необходимых алгебраических операций над
Глава 7. Координатный метод в векторами;
пространстве, 10 ч.
3) перевод результата, полученного в векторной форме, на геометрический
язык;
4) выражение скалярного, векторного и смешанного произведения векторов в
координатной форме; использование определителей второго и третьего
порядков.
И. Ф. Шарыгин
11 класс, Глава 8.
Координаты
и
пространстве, 6 ч.
векторы
1) метод координат включает в себя формулу расстояния между двумя
в точками, уравнения сферы, плоскости, прямой, векторов и их скалярное
произведение;
2) нахождения угла между прямыми, прямой и плоскостью, плоскостями вовсе
не рассматривается.
11.
Методические особенности изучениявекторно-координатного метода
перевести задачу с геометрического
языка на язык векторов
дать рекомендации, как лучше ввести
систему координат
учащимся необходимо научиться
составлять уравнение плоскости
12.
МЕТОДИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮСТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ
ПЕРВАЯ ГРУППА задач ориентирован на применение
векторно-координатного метода для решения плоских
геометрических задач. Задания строятся на использовании
ключевой терминологии векторного исчисления и метода
координат в плоскости.
ВТОРАЯ ГРУППА задач направлена на определение
наилучшего выбора системы координат, таким образом,
чтобы определенные вершины рассматриваемых
многогранников располагались на координатных осях, что
приводит к существенному упрощению вычислений.
ТРЕТЬЯ ГРУППА задач направлена на развитие умений
применения ключевых формул аналитической геометрии.
13.
МЕТОДИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮСТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ
РЕШЕНИЕ ЗАДАЧИ ВЕКТОРНО-КООРДИНАТНЫМ МЕТОДОМ СОСТОИТ ИЗ
НЕСКОЛЬКИХ ЭТАПОВ:
1. ПЕРЕВЕСТИ задачу с
геометрического языка
на векторный или
векторно-координатный;
2. ВВЕСТИ систему
координат в
пространстве наиболее
рациональным способом;
4. ПРОИЗВЕСТИ вычисления по
известным формулам;
3. НАЙТИ координаты
требуемых точек и
векторов или составить
уравнение плоскости;
5. ВОЗВРАЩАЯСЬ к исходной
задаче, перевести задачу с
векторного языка на
геометрический и записать
ответ.
14.
Система компьютерной математикиGeoGebra
15.
Дан куб ABCDA1B1C1D1. Точки E и K – середины реберсоответственно A1B1 и B1C1. Найдите угол между
прямыми AE и BK.
РИСУНОК 1. РАСПОЛОЖЕНИЕ
ЗАДАННОГО МНОГОГРАННИКА В
СИСТЕМЕ КООРДИНАТ
16.
МЕТОДИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ ВЕКТОРНОКООРДИНАТНОГО МЕТОДА К РЕШЕНИЮСТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ
РИСУНОК 1. РАСПОЛОЖЕНИЕ
ЗАДАННОГО МНОГОГРАННИКА В
СИСТЕМЕ КООРДИНАТ
17.
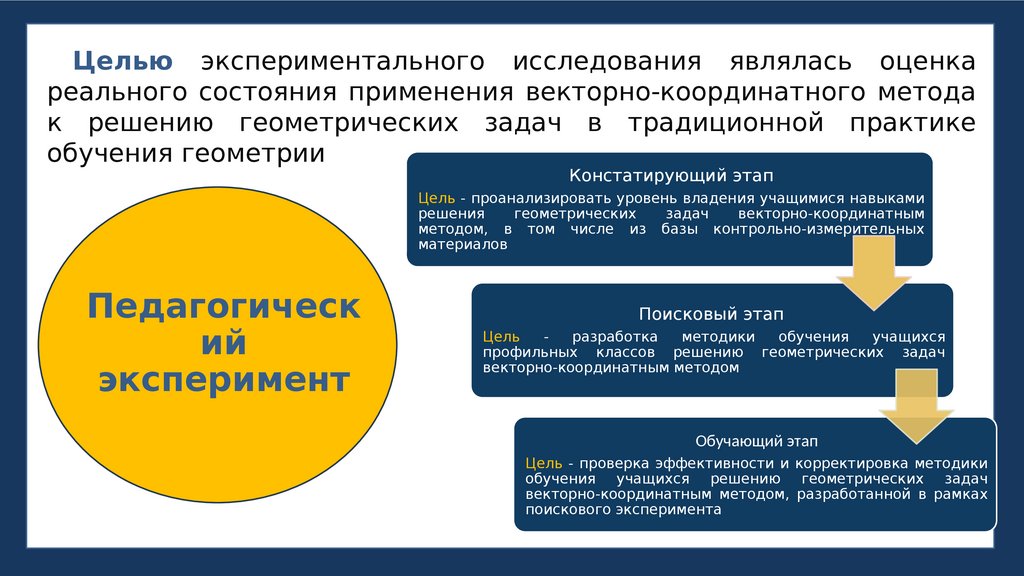
Целью экспериментального исследования являлась оценкареального состояния применения векторно-координатного метода
к решению геометрических задач в традиционной практике
обучения геометрии
Констатирующий этап
Цель - проанализировать уровень владения учащимися навыками
решения
геометрических
задач
векторно-координатным
методом, в том числе из базы контрольно-измерительных
материалов
Педагогическ
ий
эксперимент
Поисковый этап
Цель
разработка
методики
обучения
учащихся
профильных классов решению геометрических задач
векторно-координатным методом
Обучающий этап
Цель - проверка эффективности и корректировка методики
обучения учащихся решению геометрических задач
векторно-координатным методом, разработанной в рамках
поискового эксперимента
18.
Программа элективного курса «Решениегеометрических задач координатно-
III. «Понятие правильной шестиугольной призмы. Ее свойства»
векторным методом (на примере правильной
Вводное занятие
1
Основные свойства и формулы
1
Изготовление модели правильной шестиугольной призмы из
1
картона
IV. «Геометрический метод нахождения расстояний в
правильной шестиугольной призме».
Задачи на расстояние от точки до прямой
1
Задачи на расстояние от точки до плоскости
1
Задачи на расстояние между двумя скрещивающимися
1
прямыми
V. «Векторно-координатный метод нахождения расстояний в
правильной шестиугольной призме»
Задачи на расстояние от точки до прямой
1
Задачи на расстояние от точки до плоскости
1
Задачи на расстояние между двумя скрещивающимися
1
прямыми
Контрольная работа №1
1
VI. «Векторно-координатный метод нахождения углов в
правильной шестиугольной призме»
Задачи на угол между двумя прямыми
1
Задачи на угол между прямой и плоскостью
1
Задачи на угол между двумя плоскостями
1
Решение задач различными методами
1
Итоговая контрольная работа №2
1
Защита проектов
ИТОГО
шестиугольной призмы)»
Наименование темы
Кол-во
часов
I. «Векторы и координаты»
Виды систем координат
1
Понятие вектора, линейные операции нал векторами, 1
коллинеарность векторов
7
Компланарные векторы. Разложение вектора по трем 1
некомпланарным векторам
Декартовы прямоугольные координаты вектора в 1
пространстве, линейные операции над векторами в
пространстве
Скалярное произведение векторов в координатах
1
Уравнение плоскости
1
Самостоятельная работа № 1
1
II. «Векторно-координатные методы решения задач на
вычисление расстояний и углов»
Задачи на вычисления расстояния в пространстве векторно- 5
кординатным методом
Задачи на вычисления углов в пространстве векторно- 5
кординатным методом
Самостоятельная работа № 2
1
11
3
3
4
4
2
34
19.
РЕЗЕЛЬТАТ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА НАДУЧЕНИКАМИ 10 КЛАССОВ НА БАЗЕ МОУ «СОШ № 11» Г. О.
САРАНСК.
20.
СИСТЕМАТИЧЕСКАЯ РАБОТА ПО ОВЛАДЕНИЮ ВЕКТОРНОКООРДИНАТНЫМ МЕТОДОМ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХЗАДАЧ ПОЗВОЛЯЕТ:
УСИЛИТЬ
межпредметную
составляющую в
изучении
математических
дисциплин школьного
курса;
ФОРМИРОВАНИЮ
устойчивой мотивации
учащихся у учебной
деятельности;
ВЫРАБОТАТЬ
необходимые навыки
решения
стереометрических
задач данным
методом;
ПРЕОДОЛЕНИЮ
психологического
барьера перед
сложными,
нестандартными
геометрическими
задачами;
СФОРМИРОВАТЬ
представления о
преимуществах и
недостатках
различных методов
решения
стереометрических
задач;
ОБЕСПЕЧЕНИЮ
учащихся
альтернативными,
более рациональными
методами решения
стереометрических
задач.
СПОСОБСТВУЕТ
повышению
познавательного
интереса к изучению
геометрии;
21.
Основные выводы и результатыТематика решения геометрических задач непрерывно исследуется и описывается многими
авторами. Векторно-координатный метод необходим при изучении геометрии в школе. Этот
метод позволяет упростить процесс и сократить ход решения задачи, помогает учащимся
при сдаче ЕГЭ, а в дальнейшем и при изучении математики в высших учебных заведениях
Раскрыты особенности векторно-координатного метода решения задач стереометрии.
Указаны требования, предъявляемые к знаниям, умениям и навыкам учащихся,
необходимые для решения задач векторным методом.
Разработана конкретная методика формирования решения геометрических задач векторнокоординатным методом, предназначенная для старшеклассников с целью углубления,
обобщения знаний и умений учащихся по стереометрии на основе выделенных
методических особенностей.
22.
23.
ааСПАСИБО ЗА
ВНИМАНИЕ!




















 mathematics
mathematics








