Математическое моделирование экологической системы

1.

6 мая 2024 г.
МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ ЭКОЛОГИЧЕСКОЙ
СИСТЕМЫ
§3.4.5.

2.

ПОСТАНОВКА ЗАДАЧИ
экологической системе, состоящей из двух
популяций живых организмов, одна из которых
существует исключительно за счет поедания
представителей другой.
Такую систему принято называть
«хищник-жертва».
Например:
волки и овцы,
лисы и зайцы,
щуки и караси

3.

ПОПУЛЯЦИЯ
совокупность особей одного вида, существующих в
одно и то же время на определенной территории.

4.

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Пусть Ni – численность популяции жертв,
Сi — численность хищников в некоторый
момент времени ti .
Шаг по времени ∆t — конечная величина.
Примем t0 = 0 — начальный момент времени
наблюдений;
ti = i ∆t, i = 1, 2, 3, ... .

5.

ЧИСЛЕННОСТЬ ПОПУЛЯЦИИ
Исследование экспоненциального роста
начато еще Леонардо Фибоначчи (1170–
~1250) и Томасом Мальтусом (1766–1834).
Где DNi — это скорость изменения численности жертв, а
DCi — скорость изменения численности хищников.

6.

СКОРОСТЬ РОСТА ПОПУЛЯЦИИ
В рассматриваемой системе «хищник-жертва»
происходят процессы, способствующие как
росту численности популяций (скорость —
положительная величина),
так и убыванию численности (скорость —
отрицательная величина).

7.

ДОПУЩЕНИЯ
1. При отсутствии хищников скорость роста численности
популяции жертв пропорциональна DN >0, r их количеству.
2. Вклад наличия хищников в скорость убывания
популяции жертв пропорционален а произведению
численностей обеих популяций.
3. При отсутствии пищи (жертв) скорость DCi <0 убывания
популяции хищников пропорциональна q их численности.
4. Скорость роста популяции хищников благодаря
поеданию жертв пропорциональна f произведению
численностей обеих популяций — с поправкой на
эффективность рождения потомства у хищников в
результате поедания жертв.

8.

СОСТАВЛЕНИЕ СПИСКА ПАРАМЕТРОВ МОДЕЛИ
r — параметр скорости роста популяции жертв при
отсутствии хищников (отражает допущение 1);
а — параметр эффективности поиска хищниками
жертв (отражает допущение 2);
q — параметр скорости снижения популяции
хищников при отсутствии пищи (отражает допущение 3);
f — параметр эффективности рождения потомства у
хищников в результате поедания жертв (отражает
допущение 4).

9.

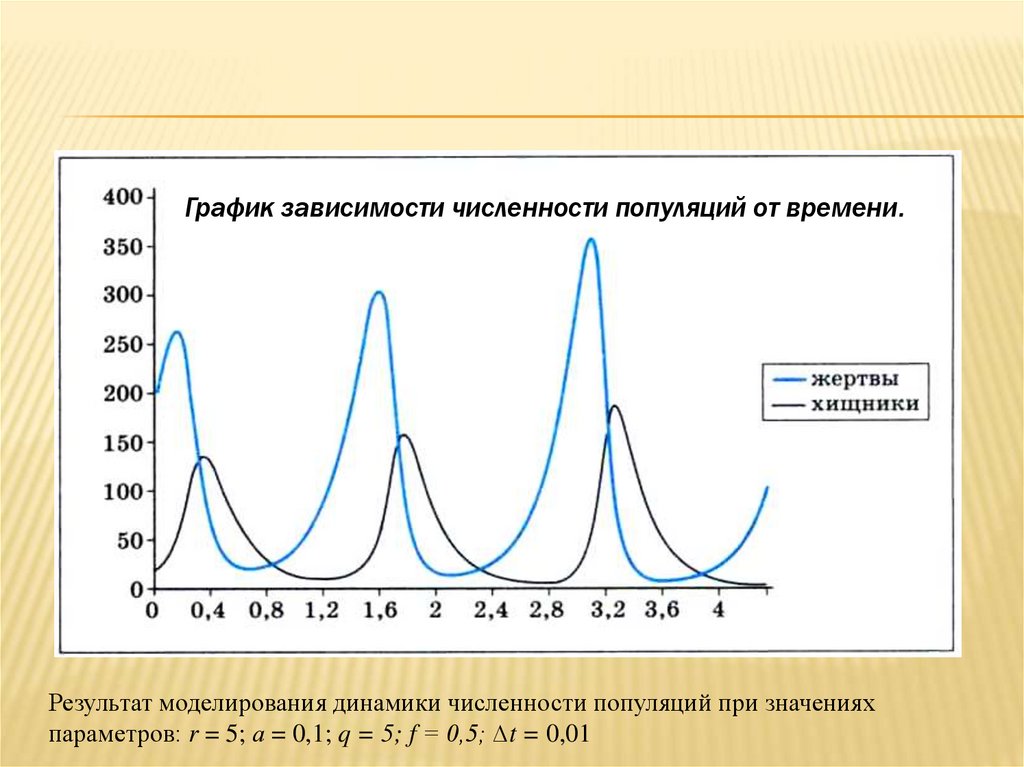
ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Входные параметры
N0 = 200, С0 = 25.
Параметры модели: г = 5; а = 0,1; q = 5; f = 0,5.
При вычислениях использовался
шаг по времени ∆t = 0,01.
Выходные параметры
1. График зависимости численности
популяций от времени.

10.

ОФОРМЛЕНИЕ ПРОГРАММЫ
1. Информационное поле с необходимыми
пояснениями
2. Начальные данные
3. Расчеты
4. График

11.

График зависимости численности популяций от времени.
Результат моделирования динамики численности популяций при значениях
параметров: r = 5; а = 0,1; q = 5; f = 0,5; ∆t = 0,01

12.

АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
При каком соотношение размеров
популяций, при котором численность, по
крайней мере, одной из них остается
неизменной?
DNi = rNi – aCiNi = 0
— условие стабилизации Ni. жертв
— условие стабилизации Сi. хищников

13.

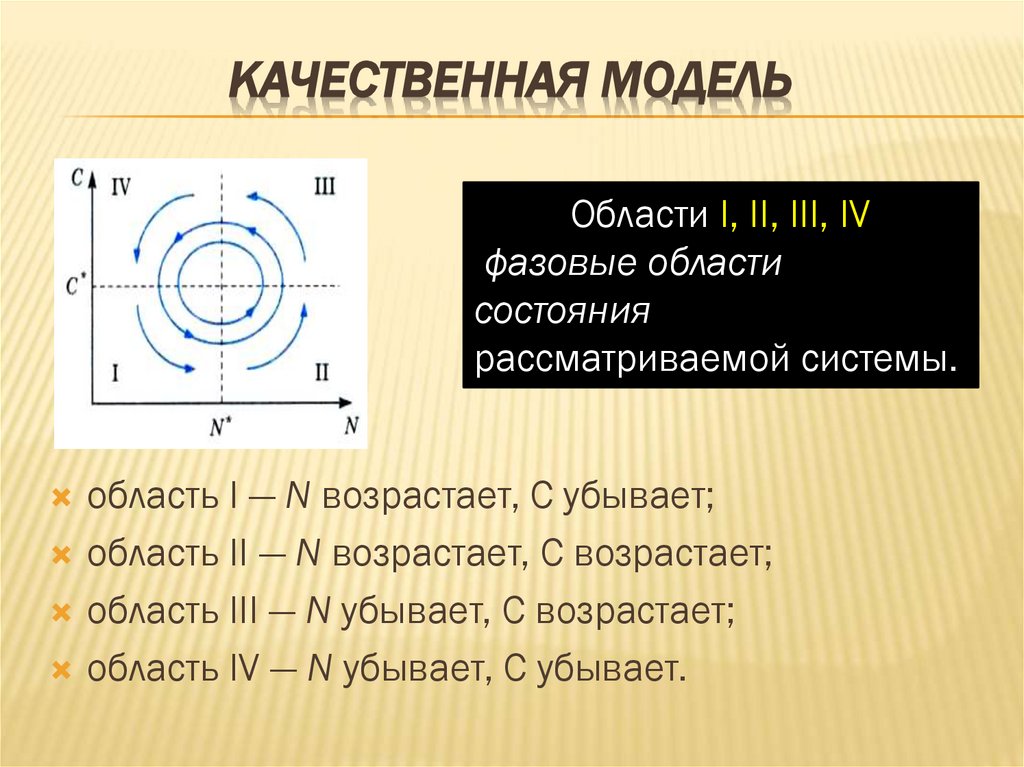
КАЧЕСТВЕННАЯ МОДЕЛЬ
Области I, II, III, IV
фазовые области
состояния
рассматриваемой системы.
область I — N возрастает, С убывает;
область II — N возрастает, С возрастает;
область III — N убывает, С возрастает;
область IV — N убывает, С убывает.