Similar presentations:
Методика изучения трехмерных геометрических фигур
1.
Реферат на тему:«Методика изучения
трехмерных геометрических
фигур»
2.
В настоящее время создаются учебные программы по геометрии, которыепри всем многообразии образовательных целей решают три задачи.
1. Преодоление существенного разрыва между изучением плоских и пространственных фигур.
2. Создание у учащихся гибких, многомерных пространственных образов, включающихся в единстве
топологические, проективные, метрические свойств и отношения изучаемых объектов.
3. Сочетание инвариантного и вариантного учебного материала, позволяющего учитывать
познавательный профиль ученика, его индивидуальную избирательность к виду и форме предлагаемых
заданий и упражнений
3.
Методика изучения геометрического материалаВ курсе математики начальной школы геометрический материал излагается
фрагментарно и не представляет собой систему. Чтобы ввести школьника в мир
геометрии на основе рассмотрения окружающего мира, необходимо учить его при
восприятии предметов выделять и абстрагировать их геометрические свойства, видеть
в них модели геометрических объектов, т.е. создавать геометрические образы. Именно
они являются основой геометрических понятий.
В начальной школе у учащихся формируются обобщенные представления или образыпонятия. Сформированность геометрического понятия предполагает умение
рассматривать его в системе понятий, а также владение кванторами и законами логики,
что возможно только в основной школе и требует определенной логической подготовки
младших школьников. Поэтому, согласно принципу природосообразности, разумно
предлагать учащимся не определения, а описания понятий, которые направлены на
создание геометрических образов.
4.
Заботясь о развитии ребенка при изучении геометрии, учитывая естественноеразвитие,
целесообразно
организовывать
реализацию следующих этапов:
- актуализация знаний;
- введение понятия;
- получение модели, если это возможно;
- некоторые свойства геометрических фигур;
- связи с ранее изученными понятиями;
- применение знаний в различных ситуациях.
процесс
обучения
геометрии
через
5.
Первымэтапом
формирования
геометрических
представлений
пространственных фигур – восприятие геометрических фигур как целостного образа.
На этапе актуализации знаний выделяем в жизненной ситуации объект определенной
формы. Эту работу можно вести в следующих направлениях:
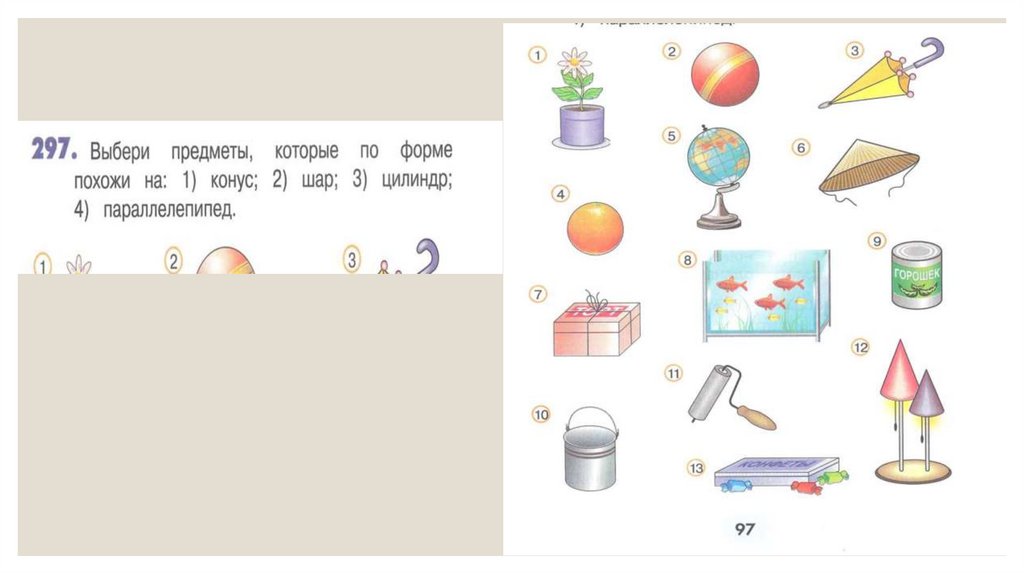
a)
Сравнение различных реальных предметов и выделение групп предметов, сходных по
форме.
b)
c)
Подбор других подходящих по форме предметов к выделенным группам.
Сравнение выделенных по сходству формы предметов с моделями объемных
геометрических фигур и выбор соответствующих моделей, знакомство с названиями
выбранных моделей.
6.
На следующем этапе вводятся понятия. Определения понятий детям не сообщаются, исоответственно от учащихся не требуется их знания.
Для усвоения существенных признаков понятия целесообразно использовать такие
приемы как сравнение и классификация.
Дети должны научиться практически использовать соответствующие признаки при
узнавании различных фигур, их классификацию.
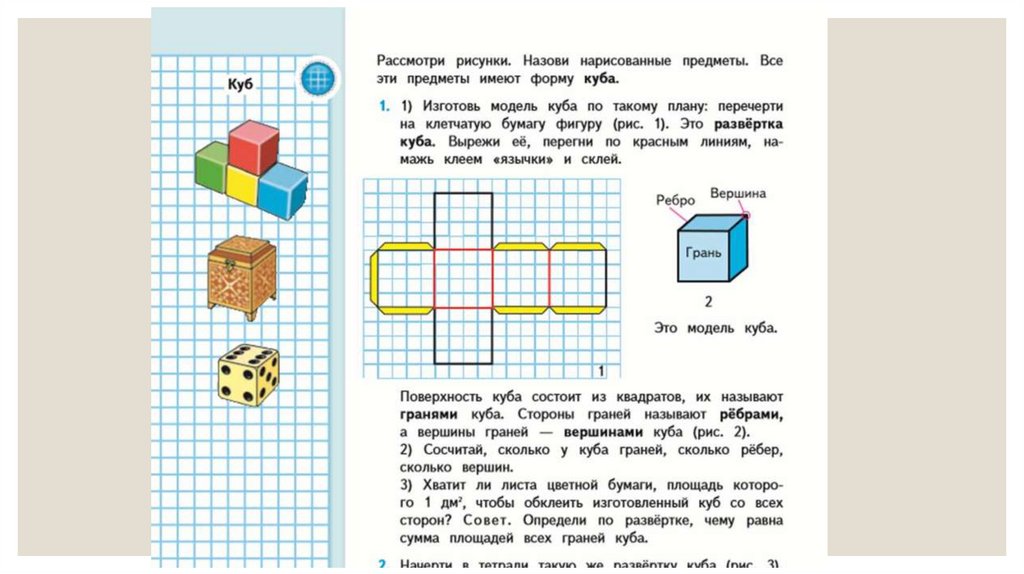
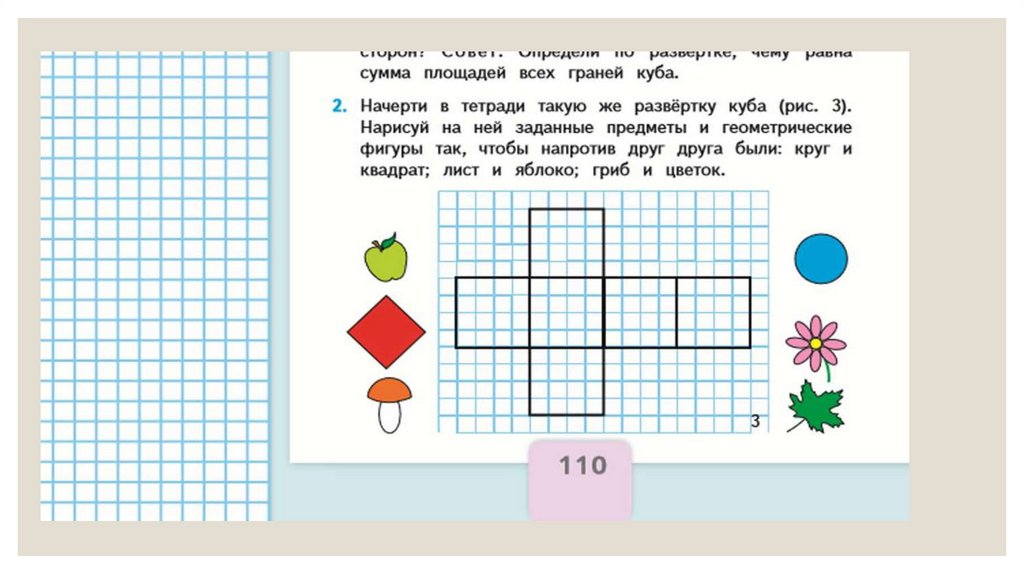
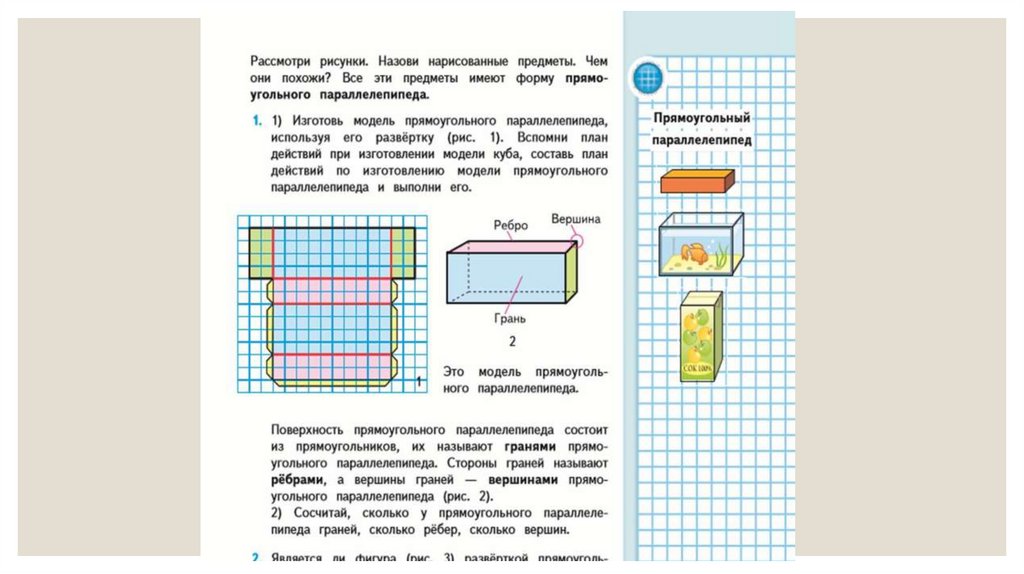
Следующей задачей после знакомства- это узнать, как называются элементы куба
(грани, вершины, ребра) их количество.
Данное направление позволит связать в единое целое объемные и плоскостные фигуры,
где плоскостные фигуры выступят в своей естественной для трехмерного пространства
роли - части объемного тела. Например, круг выступит как часть поверхности конуса
или цилиндра, прямоугольник - как часть поверхности призмы, треугольник пирамиды и т.д.
7.
Следующий этап: получение модели, если это возможно.При
выполнении
конструктивных
заданий
дети
работают
с
различными
материалами: конструктором, палочками, ленточкой, листом бумаги. Развитие
пространственного мышления невозможно отделить от формирования умений
мысленно представлять различные положения предмета, изменения его формы и
положения в зависимости от точки зрения, различных поворотов и трансформаций,
умением зафиксировать это представление на изображении. Известно, что базой для
развития пространственного мышления являются пространственные представления,
которые отражают соотношения и свойства реальных предметов, то есть свойства
трехмерного видимого или воспринимаемого пространства.
8.
После учащиеся на основе наглядных представлений, знакомятся с понятием«часть фигуры». Можно рассмотреть вопросы:
1.
назови известные нам различные части многогранников и тел вращения.
2.
«отрежем» от куба некоторую часть; какими известными вам фигурами может быть
эта часть?
3.
назови части плоских фигур.
9.
Затем проводится работа по введению понятия пересечения фигур. Сначала сучащимися рассматриваются упражнения:
1.
возьмите два одинаковых куба и приложите их друг к другу так, чтобы какая-
нибудь часть одного куба была одновременно частью и другого куба, т.е. была
общей частью этих двух кубов; покажите случай, когда общей частью будет
вершина, ребро грань, часть ребра, часть грани, точка, отрезок.
2.
может ли общей частью двух кубов быть прямая, луч, плоскость?
3.
с помощью моделей покажите случай, когда пересечением двух равных кубов
является вершина, точка, ребро, отрезок, квадрат, грань, треугольник.
10.
Еще одним из направлений в рассмотрении объемных фигур являетсясравнение моделей различных наименований. Этот материал изучается на
ознакомительном уровне. Например, сравнивая модели шара, цилиндра, конуса,
учащиеся находят общее для них – это способность катиться. Различия этих тел в
том, что у шара нет ни вершин, ни оснований, у цилиндра – два основания, но нет
вершин, у конуса – одно основание и одна вершина. Так же аналогично
рассматриваются и сравниваются другие тела: пирамида и конус, пирамида и
призма, цилиндр и призма и др.
11.
Анализ программ по математике напредмет содержания геометрического
материала
12.
В программе М.И. Моро трехмерные геометрические фигуры изучаю в 4 классе4 четверти в разделе «Материал для расширения и углубления знаний»
Учащийся получает возможность научится:
распознавать,
различать
и
называть
геометрические
тела:
прямоугольный
параллелепипед, пирамиду, цилиндр, конус;
изготавливать модель куба, прямоугольного параллелепипеда, пирамиды, конуса,
цилиндра, шара;
сравнивать геометрические тела;
находить грань, ребро, вершину куба, прямоугольного параллелепипеда, пирамиды
13.
14.
15.
16.
17.
18.
19.
20.
21.
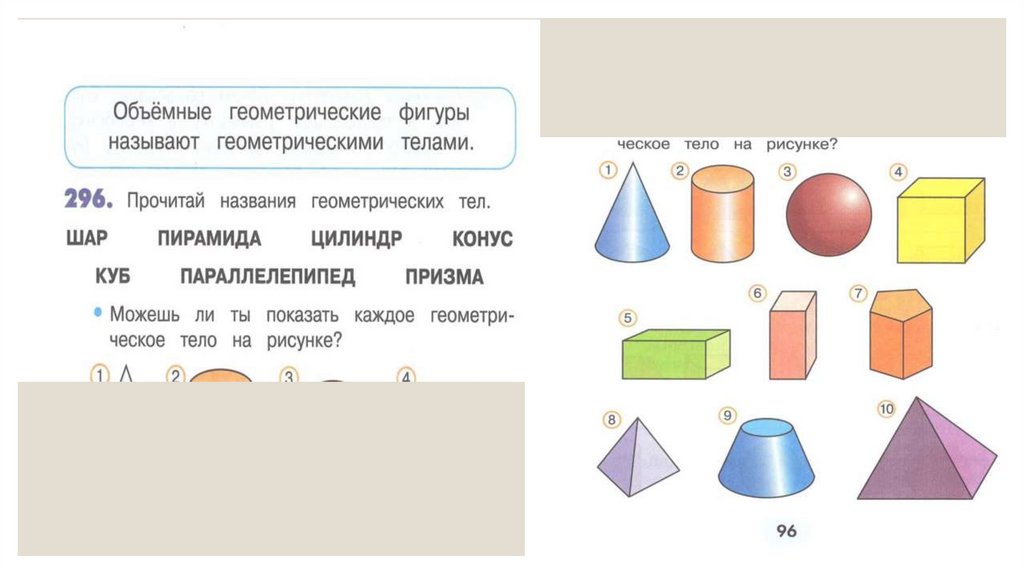
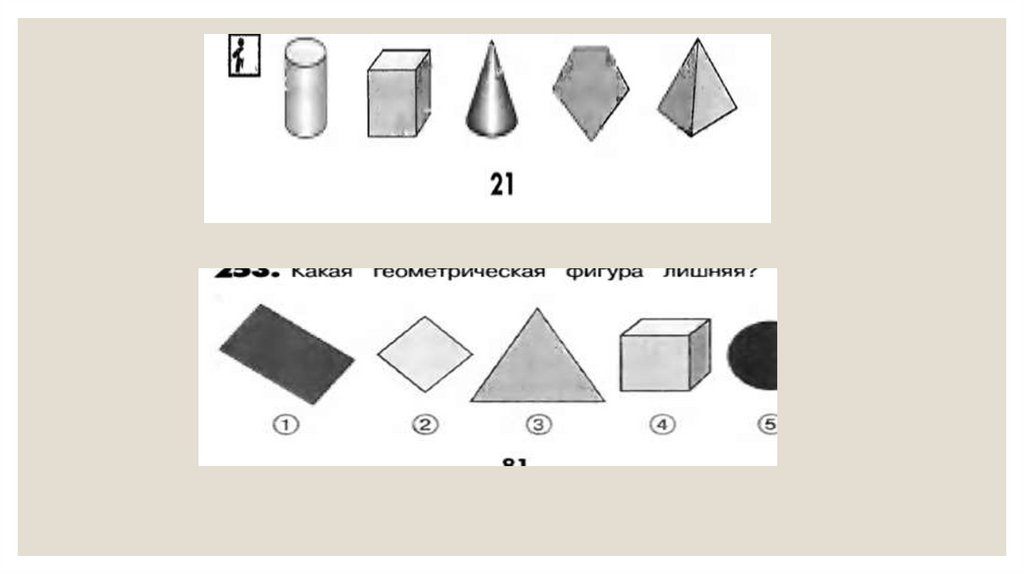
В учебниках Н.Б. Истоминой знакомство с объемными геометрическимифигурами начинается во втором классе.
Во втором классе дается представление о объемных геометрических
фигурах: шар, пирамида, цилиндр, конус, куб, параллелепипед без
введения понятий.
В разделе «Геометрические фигуры: плоские и объемные» учащимся
предлагаются задания на распознавание, целью которых является
умение различать объемные геометрические фигуры и существенные
признаки.
22.
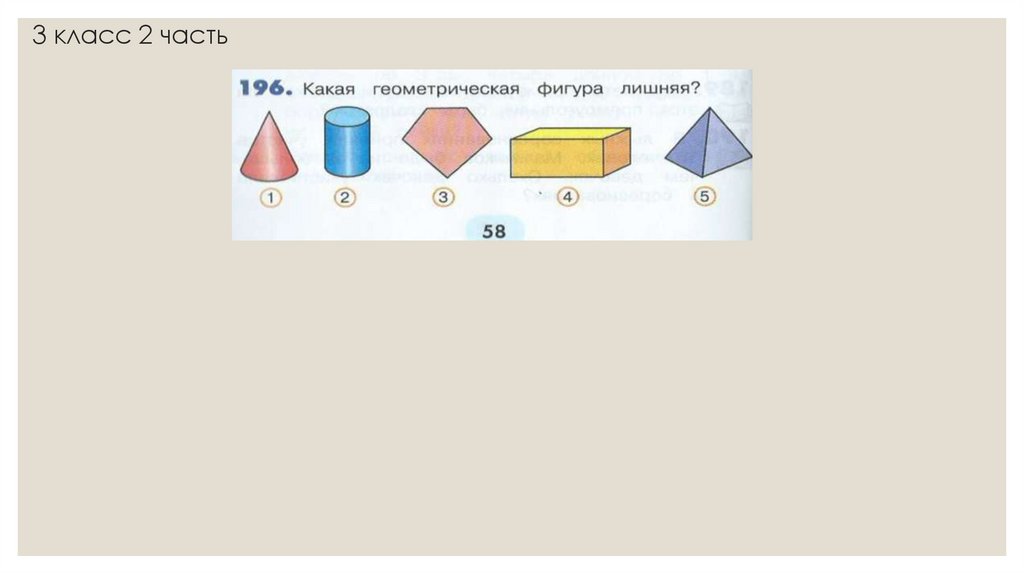
В 3 классе 2 части в разделе «Многогранники. Куб. Параллелепипед»даются понятия:
•многогранник;
•грань многогранника;
•ребро многогранника;
•вершина многогранника;
•развертка;
•куб;
•прямоугольный параллелепипед;
•пирамида.
Для развития пространственного мышления в 3 классе обучающиеся
выполняют задания на установленные соответствия между моделью куба,
его изображением и развёрткой. Для продолжения этой линии в 4 классе
используются задания на построение, распознавание и моделирование
различных объемных геометрических тел, таких как: многогранники, куб,
параллелепипед, конус, цилиндр, пирамида, призма.
23.
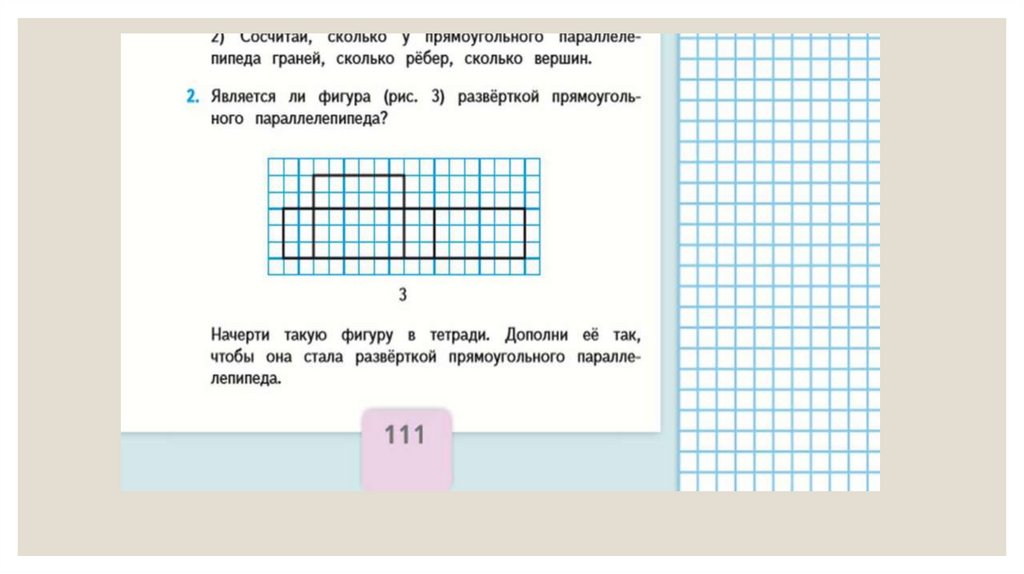
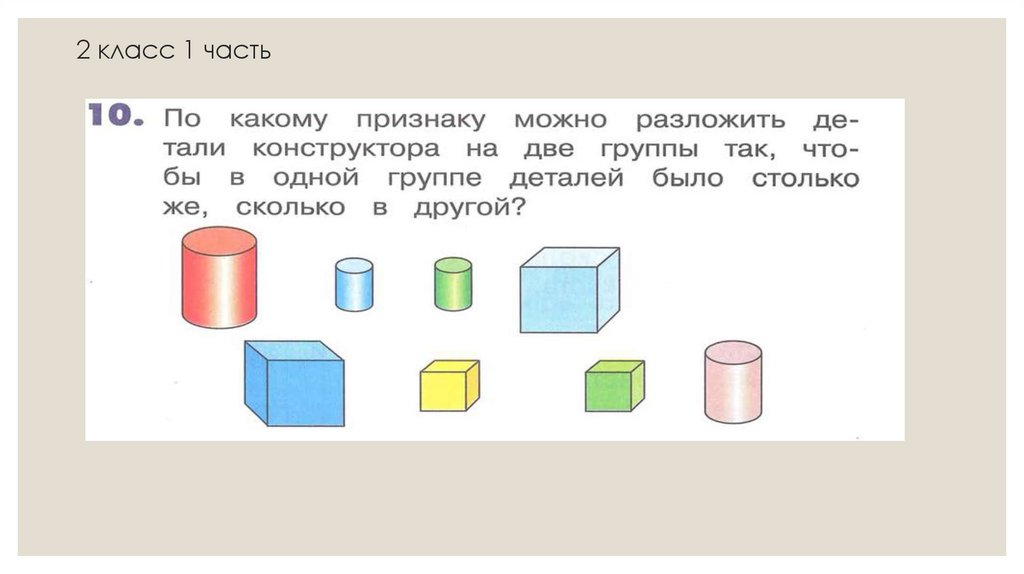
2 класс 1 часть24.
25.
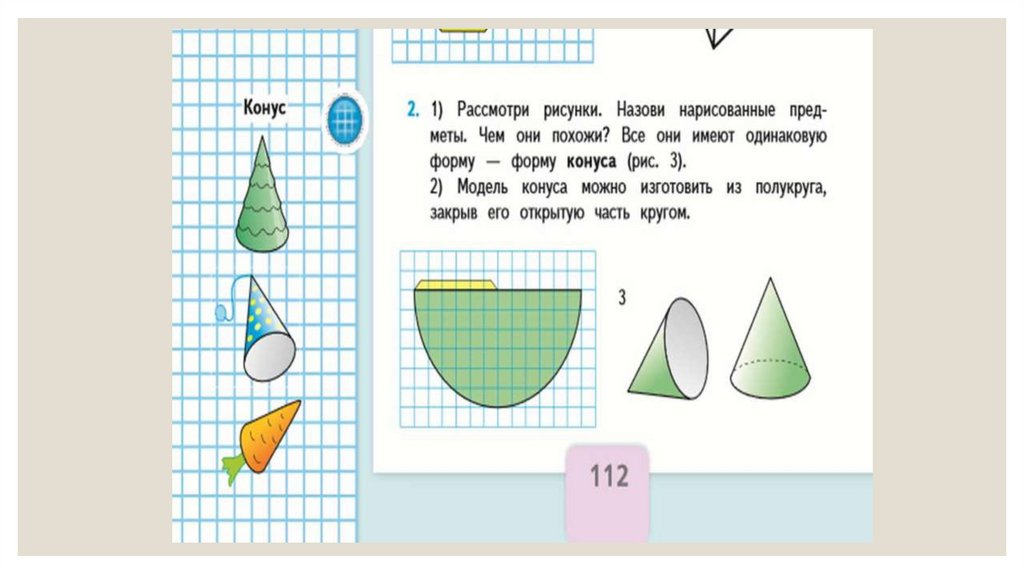
2 класс 2 часть26.
27.
28.
29.
30.
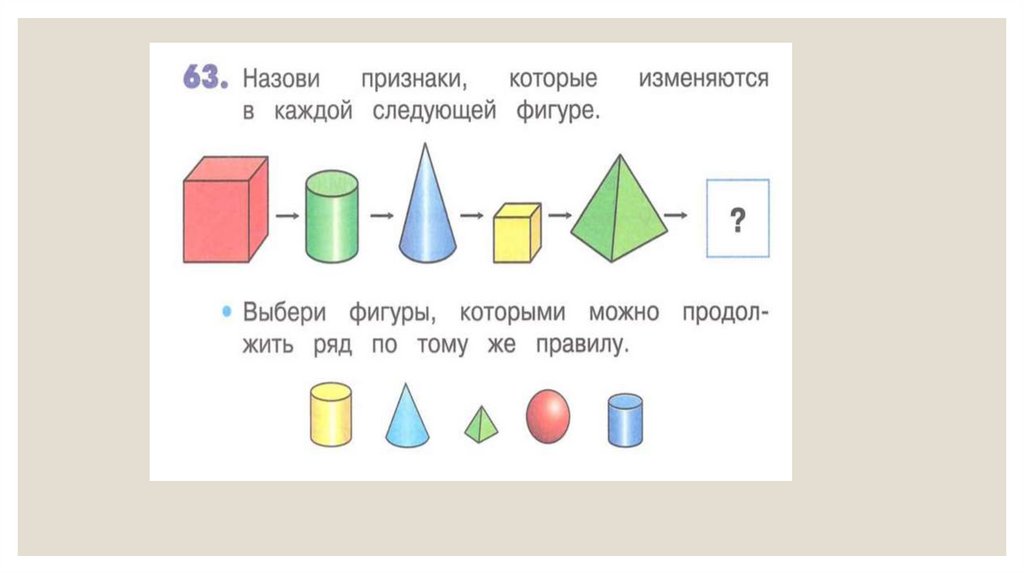
3 класс 1 часть31.
32.
33.
3 класс 2 часть34.
Само определение понятия многогранника оказывается как раз таким вопросом, где необходимо особенноВыделяют два основных способа введения понятия многогранника в школьном курсе стереометрии:
многогранник как поверхность
многогранник как тело.
Чаще используется второй путь.
Дать строгое определение понятию многогранника в школе трудно, так как в определение входят такие по
35.
Наиболее целесообразно дать описание на основе наглядных представлений школьника. Проще и короче всегНапример, у Погорелова А.В.: «Многогранник – это такое тело, поверхность которого состоит из конечного числ
36.
При этом в согласии с наглядным представлением подразумевается следующее:Имеется в виду конечная часть пространства; конечная в смысле конечности её размеров, или, как принято го
Многоугольники, ограничивающие многогранник, присоединяются к нему (содержаться в нем). Они образуют е
37.
Многогранник, и даже одна его внутренность, состоит из одного куска, или, как принято говорить в математикПоэтому, например, два куба, приставленные один к другому по ребру, т. е. имеющие общее ребро и ничего б
Все сказанное содержится в наглядном представлении о многограннике и явно оговаривается для того, чтобы
38.
Дадим строгое определение многогранника, предложенное А.Д. Александровым.Начнем с кратких предварительных определений; все они относятся как к пространству, так и к плоскости.
Фигура – это то же, что множество точек.
Точка называется граничной точкой данной фигуры, если сколь угодно близко от нее есть точки, как принадле
Точка фигуры, не являющаяся ее граничной точкой, называется внутренней.
Множество всех граничных точек фигуры называется ее границей, а множество всех ее внутренних точек – вн
Замкнутой областью называется множество точек, обладающее следующими свойствами:
(1)Оно содержит внутренние точки, а внутренность его связна.
(2)Оно содержит свою границу, и она совпадает с границей его внутренности.
39.
Данное определение относится либо к множеству точек на плоскости, либо – в пространстве. Замкнутая облИз определения замкнутой области – как на плоскости, так и в пространстве – следует, что она состоит из вн
Оба данные выше определения равносильны. Граница замкнутой области всюду прилегает к ее внутренност
В определении замкнутой области не требуется, чтобы она была ограниченной – имела конечные размеры;
40.
Часто в само понятие тела включают требование его ограниченности – конечности его размеров, ноДадим теперь определение многоугольника и многогранника.
Многоугольником называется замкнутая область конечных размеров, граница которой состоит из кон
Многогранником называется тело конечных размеров, граница (поверхность) которого состоит из конечного ч
41.
Нередко, как уже говорилось, многогранником называют не тело, ограниченное многоугольниками, а поверхнПодобное употребление одного и того же слова в разных, хотя и тесно связанных, смыслах встречается в гео
3) Можно дать другое определение понятия многогранника, если учесть следующее: фигура, составленная из
42.
Теорема.Всякое тело, составленное из тетраэдров, является многогранником и всякий многогранник можно разбить на
В несколько уточненной форме и не пользуясь понятием тела, эту теорему можно высказать так:
Фигура является многогранником тогда и только тогда, когда ее можно составить из конечного числа тетраэдро
(1)каждые два тетраэдра либо не имеют общих точек, либо имеют только одну общую вершину, или одно обще
(2)от каждого тетраэдра к каждому можно пройти по тетраэдрам, последовательно прилегающим один к другом
Данная теорема позволяет определить многогранник как фигуру, составленную из тетраэдров так, что выполне
Такое определение, которое характеризует предмет тем способом, каким он может быть построен, называется
43.
В противоположность этому определения многогранника, рассмотренные ранее, состоят в указании его характОписательное определение многогранника позволяет судить о фигуре, является ли она многогранником или н
Как и для многогранника, конструктивные определения можно дать многоугольникам многогранной поверхност
4) Другой подход к определению многогранника представлен в книге В.Г. Болтянского «Элементарная геометр
При вейлевском изложении геометрии первоначальными понятиями являются точка, вектор и следующие опе
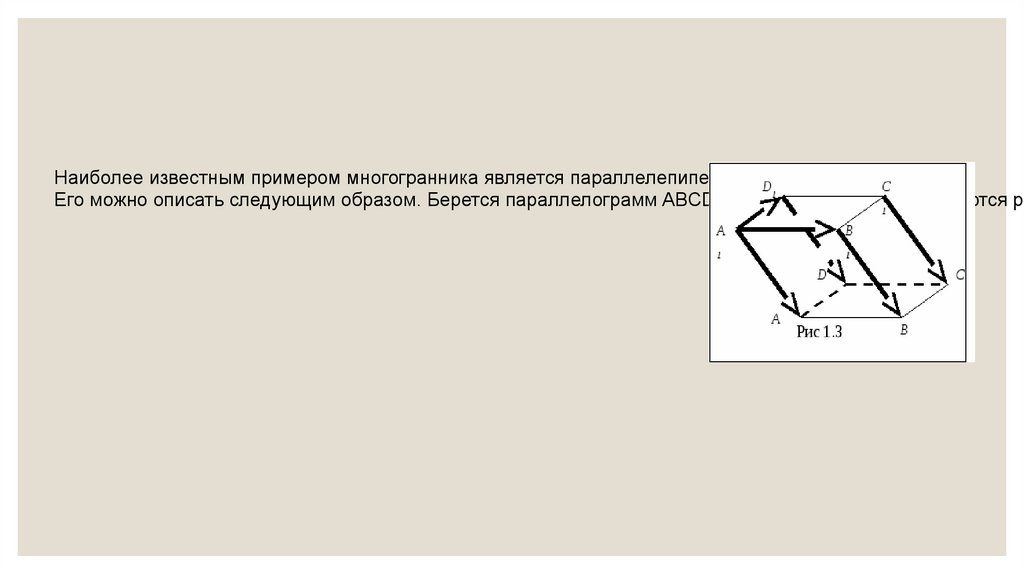
44.
Наиболее известным примером многогранника является параллелепипед.Его можно описать следующим образом. Берется параллелограмм ABCD и из его вершин откладываются ра
45.
Определение частных видов многогранников (призмы, пирамиды и др.) в данном подходе практически неТаким образом, определение многогранника может быть дано различными способами, и в разной литерат
Можно дать понятию многогранника как дескриптивное, так и конструктивное определение, как определен
Как и при введении понятия многогранника, существуют различные способы введения выпуклых многогра
46.
Подходы к определению выпуклого многогранника.После введения понятия многогранника в школе, как правило, рассматривают выпуклые многогранники
47.
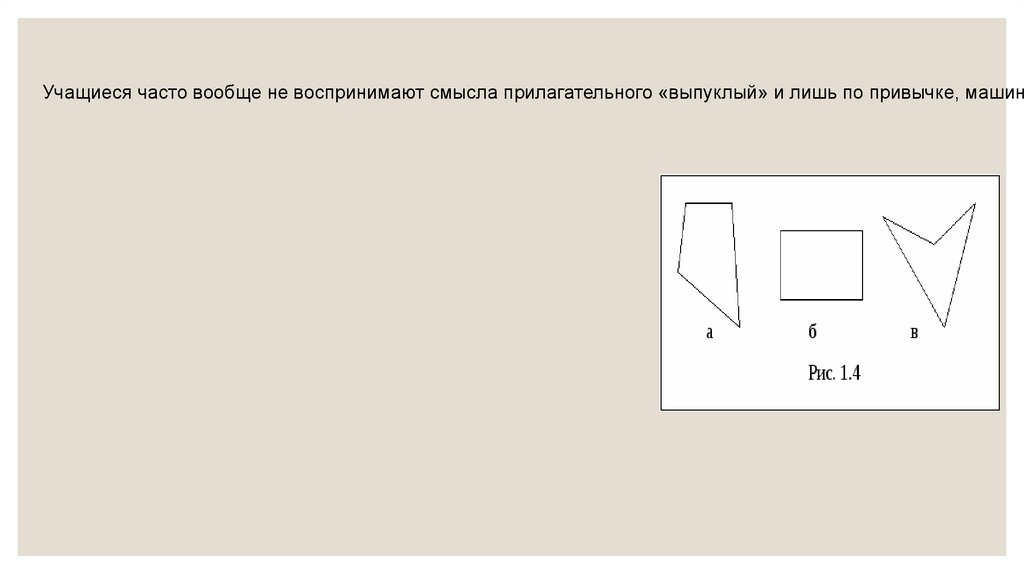
Учащиеся часто вообще не воспринимают смысла прилагательного «выпуклый» и лишь по привычке, машина48.
Понятие выпуклого многогранника чаще всего вводят по аналогии с выпуклым многоугольником.Очень хорошо эта аналогия просматривается в учебнике Александрова
Существует два способа определения выпуклого многогранника.
Многогранник называется выпуклым, если он лежит по одну сторону от каждой из ограничивающих ег
Либо многогранник называется выпуклым, если любые две его точки могут быть соединены отрезком.
49.
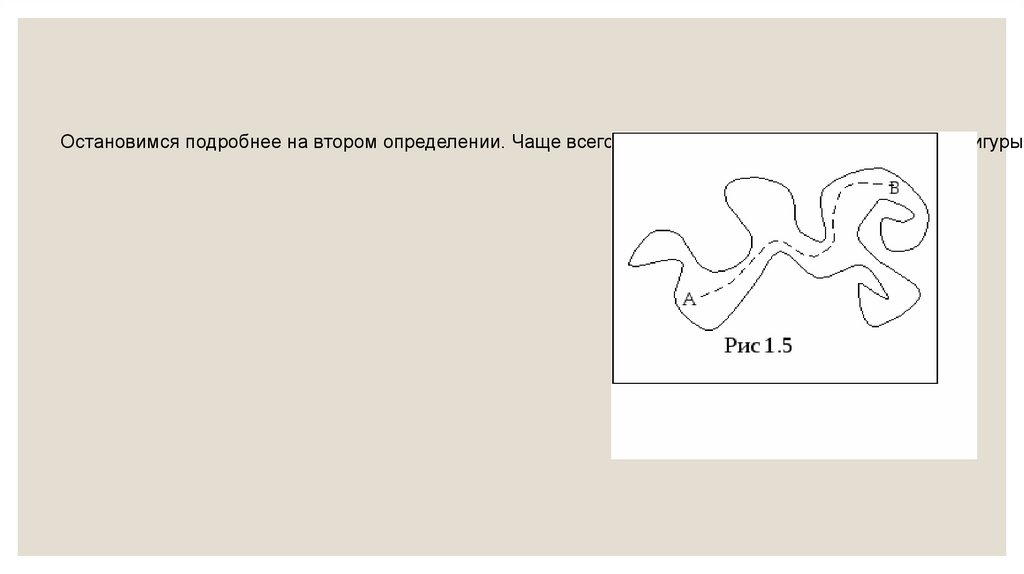
Остановимся подробнее на втором определении. Чаще всего в геометрии рассматривают связные фигуры,50.
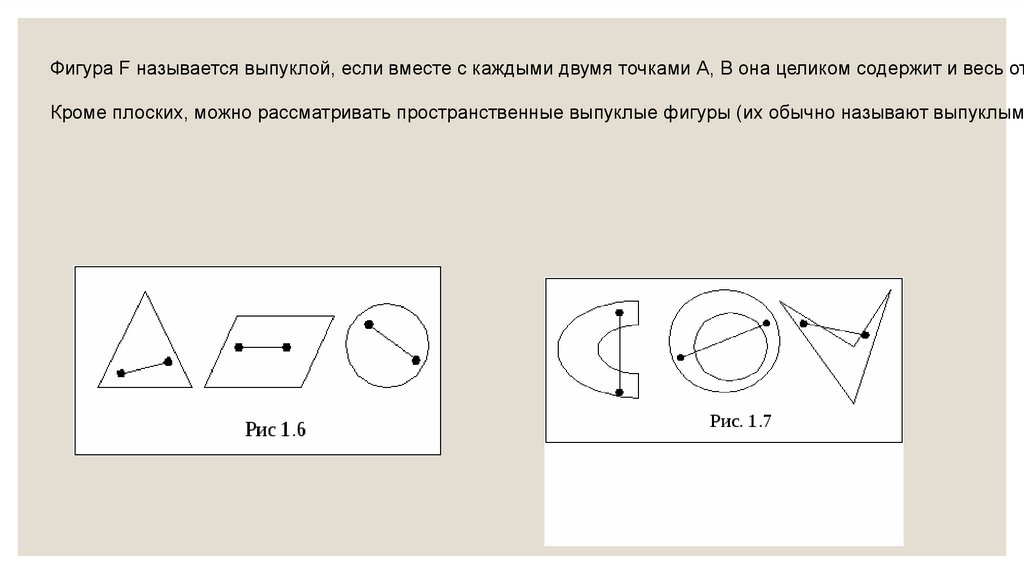
Фигура F называется выпуклой, если вместе с каждыми двумя точками А, В она целиком содержит и весь отКроме плоских, можно рассматривать пространственные выпуклые фигуры (их обычно называют выпуклыми
51.
Выпуклые тела в пространстве можно определить как пересечение некоторого множества полупространСвойство, положенное в основу определения выпуклых фигур (существование в фигуре прямолинейног
52.
Дело в том, что «произвольные» геометрические фигуры могут быть устроены необычайно сложно. НаприС другой стороны, класс выпуклых фигур является достаточно обширным. Так, все фигуры и тела, рассмат
53.
Подходы к определению правильного многогранника.После введения выпуклых многогранников изучаются их виды: призмы, пирамиды и их разновидности. Практ
В различных учебниках по стереометрии используются разные определения этого понятия. Так, в учебнике А
Учебное пособие Зив Б.Г. Задачи по геометрии дает такое определение: выпуклый многогранник называется
54.
Многогранник называется правильным, если все его грани - равные правильные многоугольники и все многоего грани равные правильные многоугольники, и все его двугранные углы равны.
Как видим, во всех перечисленных учебниках даются различные определения понятия правильного многогра
55.
Перечислим их:1°. Выпуклость многогранника.
2°. Все грани - равные правильные многоугольники.
3°. Все грани - правильные многоугольники с одним и
тем же числом сторон.
4°. В каждой вершине сходится одинаковое число ребер.
5°. Все многогранные углы имеют одинаковое число граней.
6°. Равны все многогранные углы.
7°. Равны все двугранные углы.
Возможны и другие свойства правильных многогранников,
например:
8°. Равны все ребра многогранника.
9°. Равны все плоские углы многогранника.
Какие же свойства следует взять для определения правильного многогранника? Каким методическим тре
56.
Нам представляется, что для отбора свойств в определении правильного многогранника нужно руководствовать- Всякое определение должно быть полным, т. е. включать те свойства, которые полностью определяют данное
- Всякое определение должно быть по возможности экономным, т. е. не содержать лишних свойств, которые вы
- Определение понятия правильного многогранника должно отражать уже имеющиеся представления учащихся
- Определение понятия правильного многогранника должно быть пространственным аналогом определения пон
- Определение правильного многогранника должно допускать возможные обобщения, например, на случай полу
- Определение должно быть педагогически целесообразным, т. е. свойства, включенные в него, должны в той ил
57.
Пространственными аналогами определения правильного многоугольника являются определения, данные вДля определения топологически правильных многогранников следует использовать свойства, носящие топол
58.
Таким образом, мы видим, что ни одно из рассмотренных выше определений правильного многогранн59.
Изучение многогранников в школьном курсе математики.В школьных учебниках после изучения «бесконечно-протяженных» и в силу этого весьма абстрактных геоме
60.
Можно указать на такие две проводимые методологические линии в изучении геометрии многогранников61.
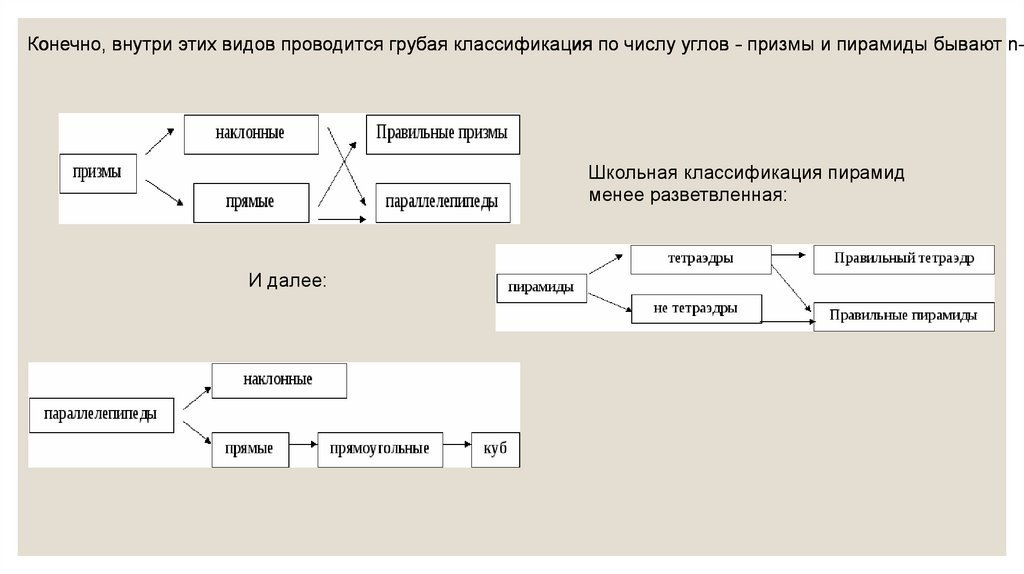
Конечно, внутри этих видов проводится грубая классификация по числу углов - призмы и пирамиды бывают n-уШкольная классификация пирамид
менее разветвленная:
И далее:
62.
Первая задача учителя - добиться от всех учащихся знания этой классификации в том виде, в каком оПричин по крайней мере три:
1) эти многогранники нужны для дальнейшего построения теории (главным образом теории объемов);
2) они обладают симметрией, как многие формы природы и творения рук человеческих (скажем, архит
3) они обладают «хорошими свойствами», т. е. для них можно сформулировать и доказать достаточно
63.
Последнее преимущество обусловлено свойствами симметричности; с другой стороны, как раз «хорошие свТретья по счету, но первоочередная для учителя задача - научить школьников решать задачи. Практически в
Рассмотрим изучение темы «Многогранники» в школьных учебниках. Для примера возьмем учебники разного
64.
Учебник Атанасяна Л.С.Рассмотрим изучение темы «Многогранники» по учебнику Атанасяна. Этот учебник предназначен для общеобр
Данная тема изучается в главе 3. На изучение ее отводится 12 уроков. Ниже приведено поурочное планирован
Номер урока
Содержание учебного материала
1-4 §1. Понятие многогранника. Призма.
Понятие многогранника. Призма. Площадь поверхности призмы. ( п.25-27)
5-9 §2. Пирамида.
Пирамида. Правильная пирамида. Усеченная пирамида. Площадь поверхности пирамиды. (п.28-30)
10 §3. Правильные многогранники.
Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогран
11Контрольная работа.
12Зачет по теме.
65.
Еще до изучения темы «Многогранники» учащиеся знакомятся с их простейшими видами в главе 1 §4 «ТетрПри объяснении понятий тетраэдра и параллелепипеда необходимо подчеркнуть, что многоугольник в прост
Для формирования у учащихся представления о способах изображения на чертеже тетраэдра и параллелеп
66.
В результате изучения параграфа учащиеся должны уметь объяснить, что называется тетраэдром, параллелепОсновная цель темы «Многогранники» - дать учащимся систематические сведения об основных видах многогр
Учащиеся уже знакомы с такими понятиями, как тетраэдр и параллелепипед, и теперь им предстоит расширит
На уроке, используя модели многогранников (куб, параллелепипед, тетраэдр, призма), необходимо назвать уча
67.
Призма А1 А2… Аn В1 В2 …Вn определяется как многогранник, составленный из двух равных многоуголь68.
Пирамида определяется как многогранник, составленный из n-угольника А1 А2 … Аn и n-треугольников. При вПри изучении теоремы о площади боковой поверхности правильной пирамиды полезна символическая запис
Sбок=n∙ S∆, Sбок=n∙hello_html_m4bf21f14.gifad, Sбок=hello_html_m4bf21f14.gif(n∙a)∙d, Sбок= hello_html_m4bf21f
Далее вводится понятие усеченной пирамиды. Плоскость, параллельная основанию пирамиды, разбивает ее
69.
При введении понятия правильной усеченной пирамиды надо отметить, что ее основания – правильные многоПоследнее, что изучается в теме «Многогранники» в учебнике , это симметрия в пространстве и понятие прав
При введении понятия правильного многогранника нужно подчеркнуть два условия, входящие в определение:
а) все грани такого многогранника – равные правильные многоугольники;
б) в каждой вершине многогранника сходится одно и то же число ребер.
В учебнике доказано, что существует пять видов правильных многогранников и не существует правильного мн
Таким образом, в данном учебнике многогранники изучаются с опорой на наглядность, предметы окружающей
70.
Весь теоретический материал темы относится либо к прямым призмам, либо к правильным призмам и прав71.
Учебник Смирновой И.М.Данный учебник предназначен для преподавания геометрии 10-11 классах гуманитарного профиля. По ср
Особенностью учебника является раннее введение пространственных фигур, в том числе многогранников
72.
Учащимся демонстрируются следующие многогранники:- куб – многогранник, поверхность которого состоит из шести квадратов;
- параллелепипед – многогранник, поверхность которого состоит из шести параллелограммов;
- прямоугольный параллелепипед – параллелепипед, у которого грани – прямоугольники;
- призма – многогранник, поверхность которого состоит из двух равных многоугольников, называемых основан
- прямая призма – призма, боковые грани которой - прямоугольники; правильная призма – прямая призма, ос
- пирамида – многогранник, поверхность которого состоит из многоугольника, называемого основанием пирам
- правильная пирамида – пирамида, в основании которой правильный многоугольник, и все боковые ребра ра
73.
Показываются более сложные многогранники, в том числе правильные, полуправильные и звездчатые многоТаким образом, к началу непосредственного изучения темы «Многогранники» учащиеся уже знакомы (на дост
Основная цель данного раздела – ознакомить учащихся с понятием выпуклости и свойствами выпуклых мног
74.
Можно привести примерное тематическое планирование данной темы.18Выпуклые многогранники
19Теорема Эйлера
20*Приложения теоремы Эйлера
21Правильные многогранники
22*Топологически правильные многогранники
23Полуправильные многогранники
23Звездчатые многогранники
Среди пространственных фигур особое значение имеют выпуклые фигуры и, в частности, выпуклые многог
После изучения выпуклых многогранников рассматривается теорема Эйлера и ее приложения. В качестве
75.
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоПри изучении правильных, полуправильных и звездчатых многогранников следует использовать модели
76.
Опорные задачи по теме «Многогранники».Как уже говорилось, изучение многогранников является важнейшей частью курса стереометрии. Они даю
Устное решение задач «на многогранники» значительно улучшает пространственное мышление учащихс
Так как основные геометрические тела, изучаемые в школе, это призмы и пирамиды, то задачи, приведен
77.
Большое количество задач можно предлагать для решения вместе с готовым рисунком, когда один рисунок78.
Задачи по теме «Призма».Для простоты введем обозначения. Буквами а, b, c обозначим соответственно длину, ширину и высоту прямоуг
1) Задачи на вычисление.
Четырехугольная призма.
Перед решением задач 1 и 2 следует повторить формулы для вычисления элементов куба со стороной a:
Задача 3 и некоторые из следующих за ней, в которых речь идет о прямоугольном параллелепипеде, потребую
D2= а2+ b2+ с2 ,d2=a2 +b2 , s = аb, Q = d ∙ с, Sб= Р∙с.
1. Ребро куба равно а. Найдите: диагональ грани; диагональ куба; периметр основания; площадь грани; площа
2. По рис. 4.1 и по данным элементам в табл. 1 найдите остальные элементы куба.
79.
3. По рис.4.2 и по данным элементам в табл. 2 найдите остальные элементы прямоугольного параллелепипед4. Перпендикулярным сечением наклонной 4-угольной призмы является ромб со стороной 3 см. Вычислите пло
5. Найдите боковую поверхность наклонного параллелепипеда с боковым ребром 32 см и смежными сторонам
6. Сторона основания правильной четырехугольной призмы равна 3 см. Высота призмы - 5 см. Найдите: диаго
7. Площадь боковой поверхности правильной четырехугольной призмы равна -32 см, а площадь поверхности 4
Треугольная, шестиугольная и n-угольная призмы.
Перед решением задач целесообразно повторить формулы; Sб = РН и Sп = 2Sб + 2s для произвольной призмы
Р = 3а, s = h - для правильной треугольной и
Р = 6а, s = h -для правильной шестиугольной призмы со стороной основания а.
80.
2)Задачи на исследование.1. Поставьте куб так, чтобы ни одна грань не была вертикальной. Будут ли тогда у него горизонтальные гран
2. Можно ли куб с ребром в 7 см оклеить листом бумаги в виде прямоугольника шириной14 см и длиной в 21
3. Сколько нужно взять прямоугольников и каким свойством они должны обладать, чтобы из них можно был
4. Установите, прямой или наклонной является призма, у которой две смежные боковые грани перпендикуля
5. Исследуйте, существует ли призма, имеющая 50 ребер? 54 ребра?
6. Какой многоугольник лежит в основании призмы, если она имеет n граней?
81.
3)Задачи на доказательство.1. В параллелепипеде диагонали основания равны, а боковое ребро перпендикулярно двум смежным сторонам
Доказательство. В основании - параллелограмм с равными диагоналями, т.е. прямоугольник, а боковое ребро п
2. Докажите, что число ребер призмы кратно 3.
Доказательство. В n-угольной призме боковых ребер n, а ребер нижнего и верхнего оснований 2n, всего 3n ребе
3. Докажите, что сумма двугранных углов при всех боковых ребрах четырехугольной призмы равна 360".
Доказательство. Рассмотрим перпендикулярное сечение призмы. В сечении - четырехугольник, сумма его углов
4. Если призма имеет 18 граней, то в ее основании лежит 16-угольник. Докажите.
Доказательство. У призмы две грани оснований и, значит, боковых граней 16. Следовательно, в основании 16-у
82.
4)Задачи на построениеСечения можно рисовать на заранее подготовленном изображении призмы.
1. Постройте сечение куба в виде: а) треугольника, б) четырехугольника, в) пятиугольника, г) шестиугольника
2 Постройте плоскость, проходящую через сторону нижнего основания треугольной призмы. Какие многоугол
Ответ: сечение может иметь форму треугольника, трапеции.
83.
Задачи по теме «Пирамида».1) Задачи на вычисление
1. В правильной четырехугольной пирамиде высота составляет с боковой гранью угол, равный 37°. Найдите уг
2. Боковое ребро правильной пирамиды вдвое больше ее высоты. Определите угол наклона бокового ребра к
3. Периметр основания пирамиды равен 20 см, а площадь ее основания 16 см2. Найдите периметр и площадь
4. Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника, лежащего в основании, и равны
5. В правильной четырехугольной пирамиде боковое ребро равно 20 см, оно составляет с основанием угол 45
Определите расстояние от центра основания до бокового ребра.
Решение. Искомое расстояние d равно длине высоты, опущенной из вершины равнобедренного прямоугольно
Ответ: 10 см.
84.
Задачи на исследование.1. Сколько вершин, ребер и граней имеет n-угольная пирамида?
Ответ: n + 1 вершин. n + 1 граней, 2п ребер.
2. Какое основание может иметь пирамида, у которой все ребра равны?
Решение. Плоские углы при вершине пирамиды равны 60°, так как каждая боковая грань - равносторонний треу
3. В каких пределах находится плоский угол α при вершине правильной n-угольной пирамиды. если n = 3, 4, 5, 6
4. У треугольной пирамиды все боковые ребра равны. Может ли высота такой пирамиды находиться на одной и
Ответ: может, если в основании прямоугольный треугольник.
5. Сравните термины: «правильная треугольная пирамида» и «правильный тетраэдр». Можно ли утверждать, чт
6. Боковые ребра пирамиды равны. Может ли ее основанием быть: а) прямоугольная трапеция, б) ромб?
Ответ: а) не может, поскольку такую трапецию нельзя вписать в окружность; б) может только в случае, если осн
85.
Задачи на доказательство.1. Докажите, что число плоских углов в n-угольной пирамиде делится на 4.
2. Если в правильной треугольной пирамиде высота Н равна стороне основания а, то боковые ребра составля
Решение. Высота пирамиды проектируется в центр окружности радиуса R, описанной около основания, α - ис
3. Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».
Решение. Основание пирамиды - правильный многоугольник. Так как боковые ребра равны, то вершина проек



































































 mathematics
mathematics