Similar presentations:
День науки
1.
Учитель математики: Первушкина ИринаМихайловна
ДЕНЬ НАУКИ В ГБОУ ЛИЦЕЙ №395
2.
3.
4.
Знаменитый французский учёный П.Лаплас говорил: «Читайте, читайте
Эйлера, он наш общий учитель».
5.
6.
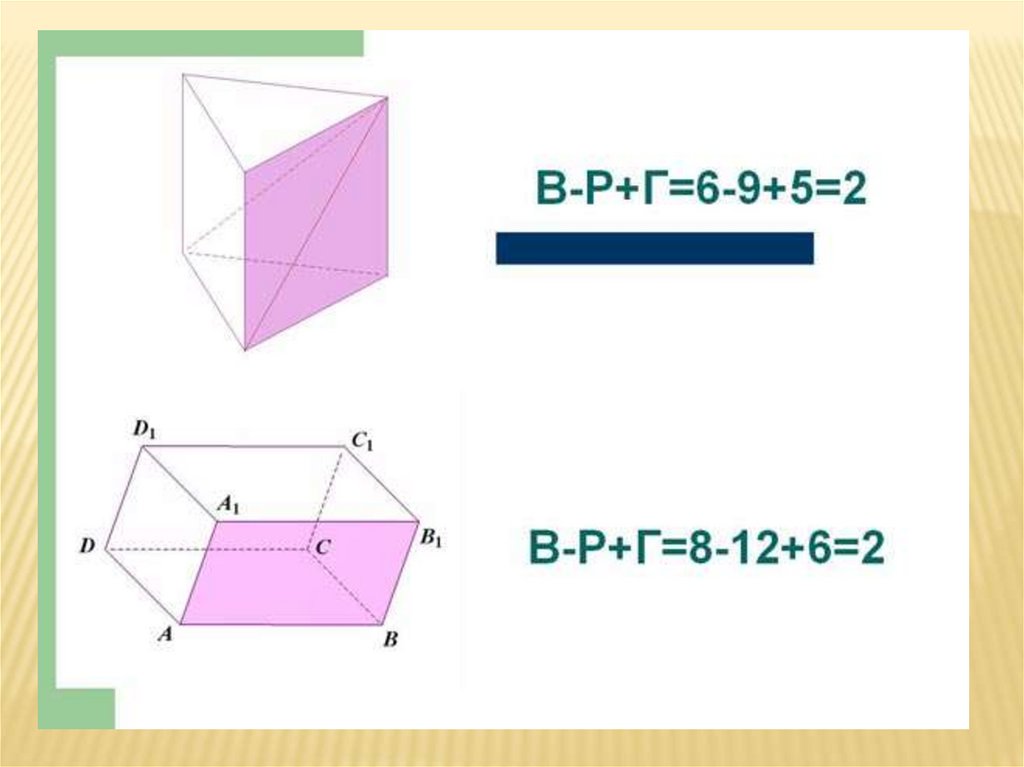
Задание 1Сейчас перед вами появятся изображения
многогранников:
треугольной
призмы,
параллелепипеда,
треугольной
пирамиды,
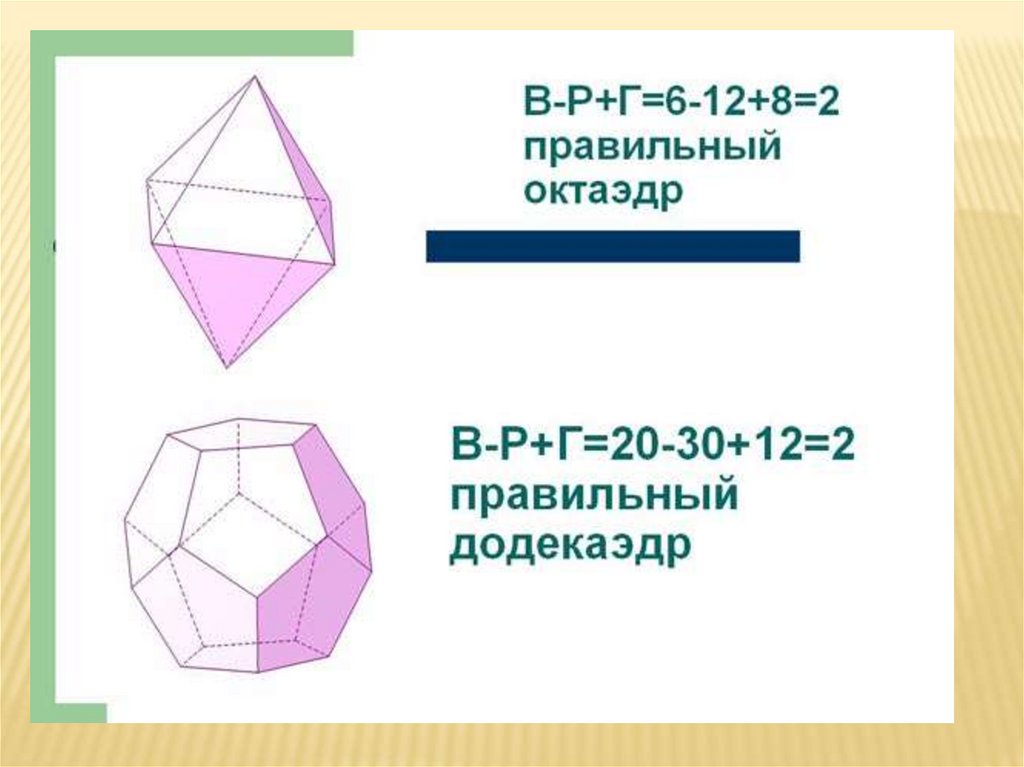
усечённой пятиугольной пирамиды, правильный
октаэдр, правильный додекаэдр. Ваша задача –
посчитать число вершин, рёбер и граней у этих
многогранников и вычислить для каждого из них
В – Р + Г = ? Найдите закономерность.
7.
8.
9.
10.
11.
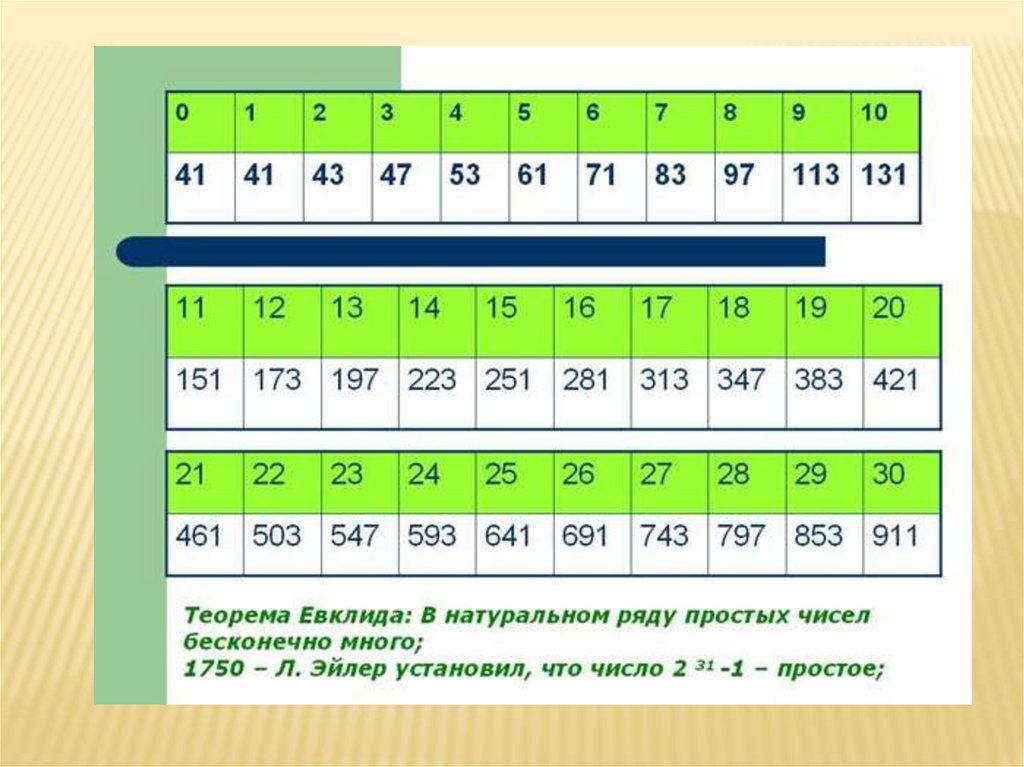
Задание 2Вам необходимо вычислить значение
этого многочлена при х от 1 до 20. За
каждый правильный ответ команда
получает 1 балл. Если вы сумеете
отгадать закономерность, то получите
ещё 10 баллов.
12.
13.
14.
15.
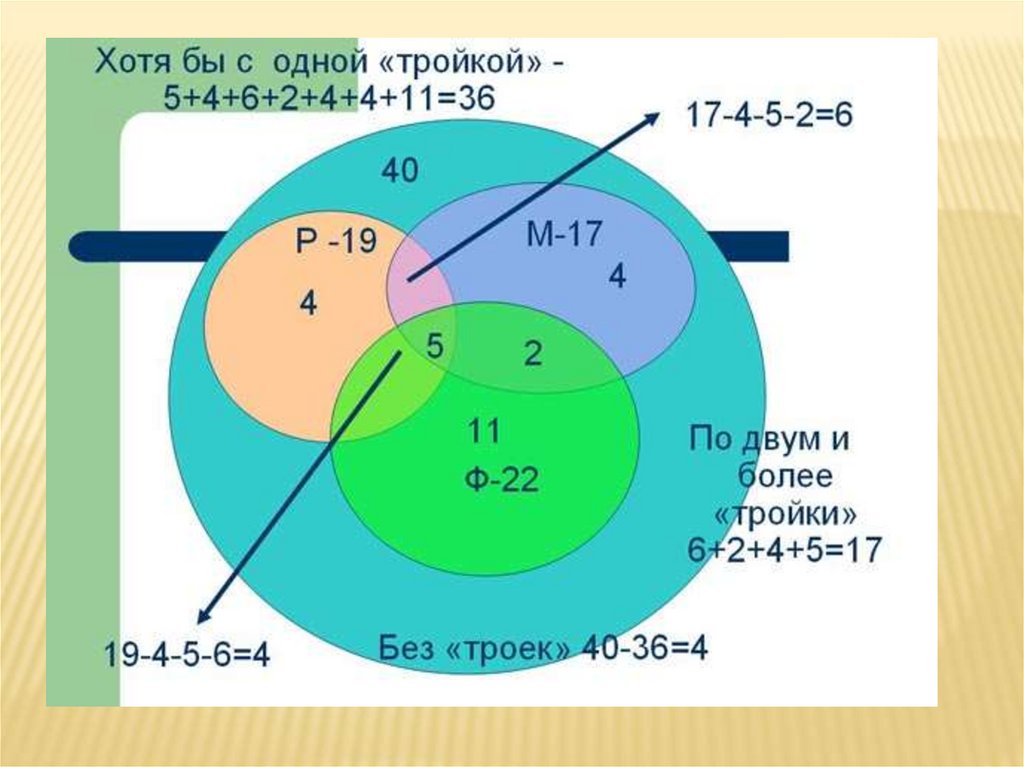
Задание 3Пересчитайте математиков. В классе 35
учеников. Из них 20 занимаются в
математическом кружке, 11 – в биологическом,
10 ребят не посещают эти кружки. Сколько
биологов увлекаются математикой?
16.
17.
Вот перевод латинского текста, который взят из письма Эйлера китальянскому математику и инженеру Маринони, отправленного из
Петербурга 13 марта 1736 года: "Некогда мне была предложена задача об
острове, расположенном в городе Кенигсберге и окруженном рекой, через
которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь
непрерывно обойти их, проходя только однажды через каждый мост. И
тут же мне было сообщено, что никто еще до сих пор не мог это
проделать, но никто и не доказал, что это невозможно. Вопрос этот,
хотя и банальный, показался мне, однако, достойным внимания тем, что
для его решения недостаточны ни геометрия, ни алгебра, ни
комбинаторное искусство... После долгих размышлений я нашел легкое
правило, основанное на вполне убедительном доказательстве, с помощью
которого можно во всех задачах такого рода тотчас же определить,
может ли быть совершен такой обход через какое угодно число и как
угодно расположенных мостов или не может".
18.
19.
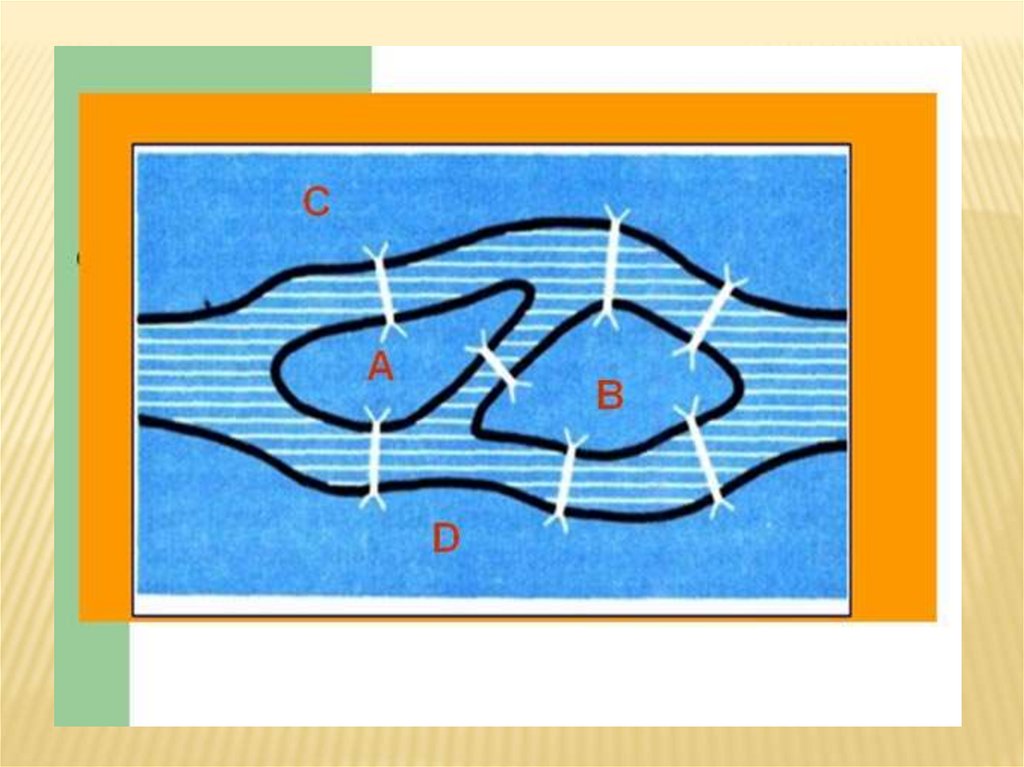
Если число островов, соединённых мостами больше двух, тодля решения задачи необходимо посчитать, сколько мостов
ведут на каждый остров.
- Если на каждый остров ведёт чётное число мостов, то
обход возможен и начать его можно с любого острова.
- Если на два острова ведёт нечётное число мостов, то
обход возможен и его следует начать с любого острова на
который ведёт нечётное число мостов.
-Если имеется более двух областей, в которое ведёт
нечётное число мостов, то указанный переход не возможен.
-В нашей задаче всего островов 4: A, B, C, D. Число мостов,
ведущих к этим участкам соответственно: 5, 3, 3, 3, значит
обход невозможен.
20.
21.
22.
Задание 4Выясните, можно ли обойти все мосты, побывав на
каждом из них только по одному разу в следующих
случаях.
23.
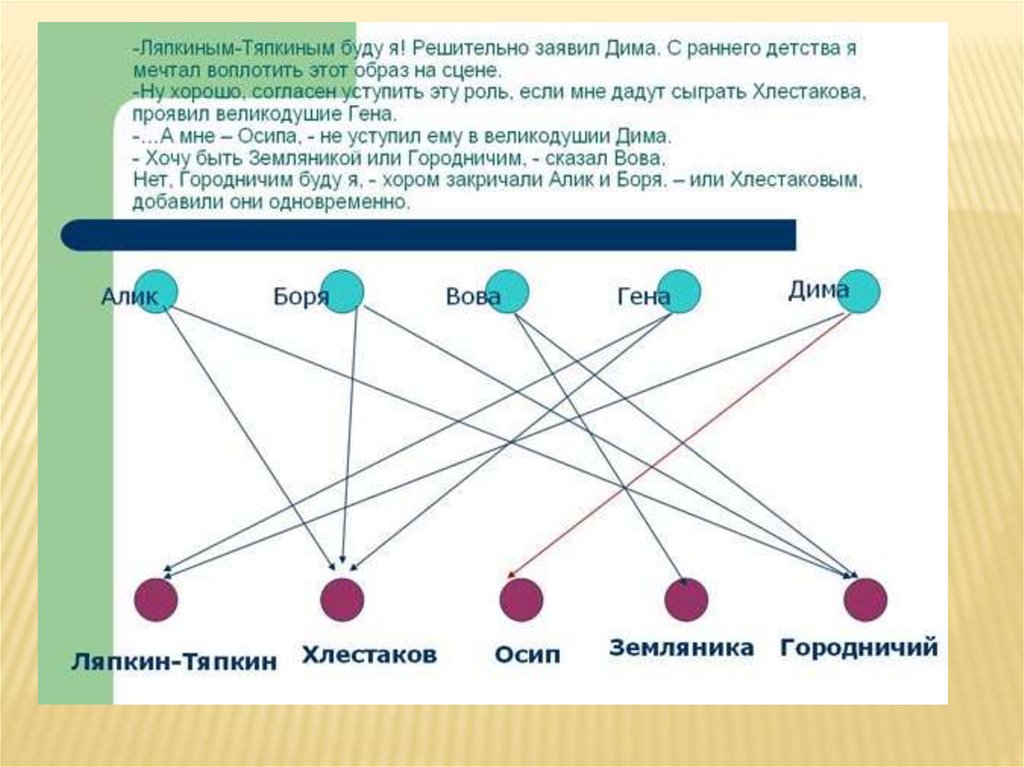
В школьном драматическом кружке решили ставитьгоголевского «Ревизора». И тут разгорелся жаркий спор. Всё
началось с Ляпкина-Тяпкина.
– Ляпкиным-Тяпкиным буду я! Решительно заявил Дима. С
раннего детства я мечтал воплотить этот образ на сцене.
– Ну хорошо, согласен уступить эту роль, если мне дадут
сыграть
Хлестакова,
проявил
великодушие
Гена.
– … А мне – Осипа, – не уступил ему в великодушии Дима.
– Хочу быть Земляникой или Городничим, – сказал Вова.
– Нет, Городничим буду я, – хором закричали Алик и Боря. –
или Хлестаковым, добавили они одновременно.
Удастся ли распределить роли так. Чтобы исполнители были
довольны?
24.
25.
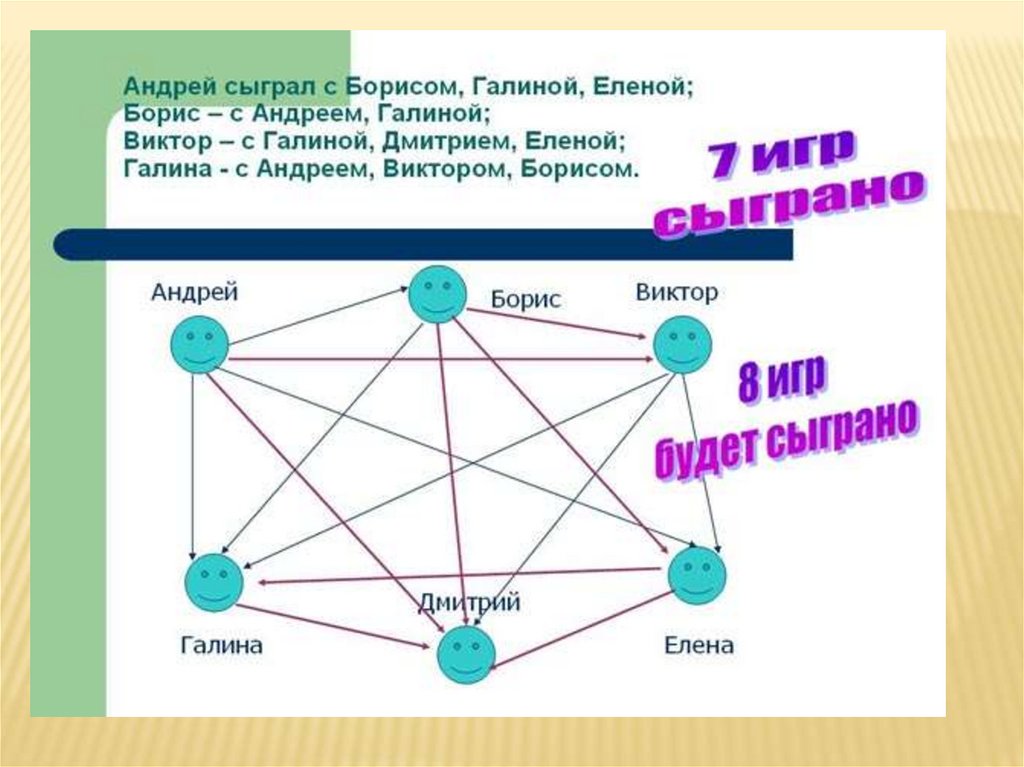
Задание 5Решите с помощью графов следующую задачу: В
первенстве класса по настольному теннису 6 участников:
Андрей, Борис, Виктор, Галина, Дмитрий и Елена.
Первенство проводят по круговой системе – каждый из
участников играет с каждым из остальных один раз.
Сколько сыграно игр?
26.
27.
Задание 7Выясните, выполнив необходимые построения на какой линии
в произвольном треугольнике лежат следующие три точки:
точка пересечения высот, точка пересечения медиан, центр
описанной окружности.
Задание 8
Требуется выбрать 5 гирь так, чтобы с их помощью можно
было взвесить любой груз до 30кг, при условии, что гири
ставятся только на одну чашу весов. Эйлер предложил взять
такие гири: 1 кг, 2 кг, 4 кг, 8 кг, 16 кг. Попробуйте «взвесить»
этими гирями грузы от 1 до 30 килограмм.





























 education
education








