Similar presentations:
Комбинаторные задачи. Правило умножения
1.
2.
«Комбинаторные задачи»3.
Слово имеет латинское происхождение, впереводе означает – «соединять»,
«сочетать»
Комбинаторика – это раздел математики,
посвященный задачам выбора и
расположения предметов из различных
множеств
4.
5.
«Вектор» 54, 51, 5241, 42, 45
12, 14, 15
21, 24, 25
«Радиус» 58, 59, 53
85, 89, 83
93, 98, 95
39, 38, 35
«Интеграл» 07, 01, 06
70, 71, 76
10, 17, 16
60, 61, 67
«Конус» 39, 34, 31
94, 93, 91
49, 43, 41
13, 19, 14
6.
Правило умноженияЕсли первый элемент некоторой пары можно
выбрать m способами и для каждого из этих
способов второй элемент можно выбрать n
способами, то пару можно выбрать
m*n
способами.
7.
Количество вариантов«Вектор»
«Радиус»
«Интеграл»
«Конус»
4*3=12 вариантов
3*2=6 вариантов
5*4=20 вариантов
4*3=12 вариантов
8.
ПримерВ турнире участвуют 4 человека. Сколькими
способами могут распределиться места
между ними?
По правилу умножения: 4*3*2*1=24 способа
распределить места.
Расположение множества в
определенном порядке называется
перестановкой.
9.
1*2*3*4 = 4!Произведение всех натуральных чисел от 1 до
n обозначается n!
Рn = n!
10.
ЗадачаВ расписании 7 класса на четверг должно быть шесть
предметов: русский язык, литература, алгебра,
география, физика, физкультура. Сколькими
способами можно составить расписание на этот
день?
Число способов равно числу перестановок из 6
элементов.
Р6 = 6! = 1*2*3*4*5*6 = 720
способов
11.
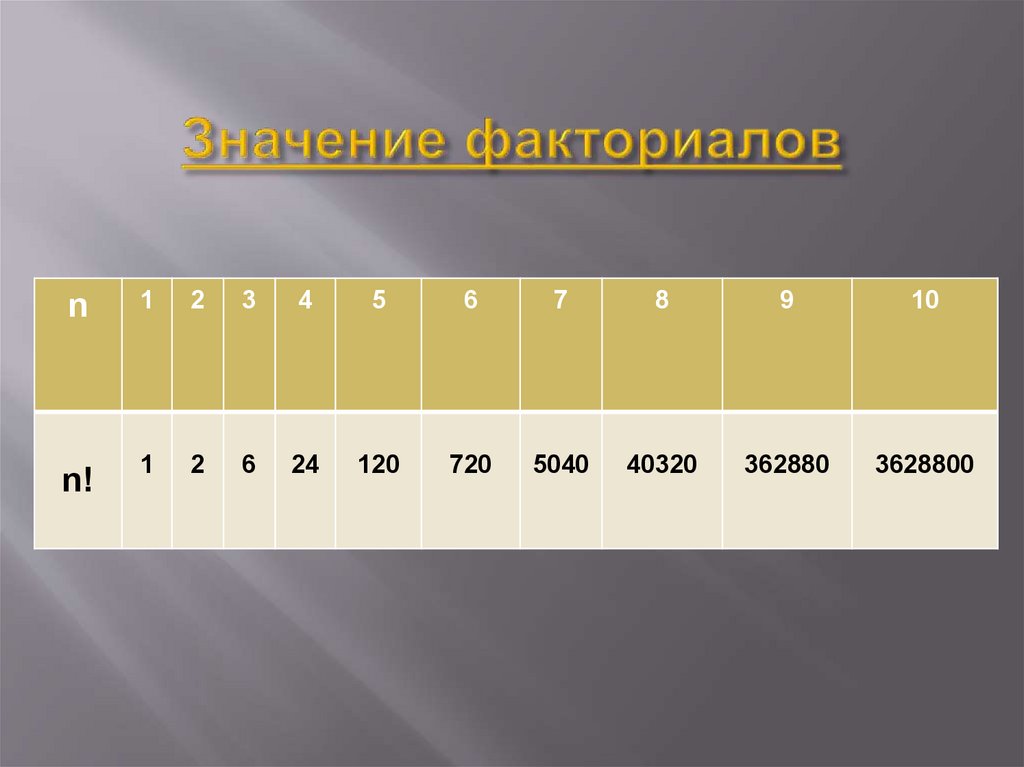
n1
2
3
4
5
6
7
8
9
10
n!
1
2
6
24
120
720
5040
40320
362880
3628800
12.
«Вектор» 17640 руб«Радиус» 8640 руб
«Интеграл» 5184 руб
«Конус» 3227 руб
13.
Домашняя работа.П. 6.3 ; 6.4
№ 587, 599, 609













 mathematics
mathematics








