Similar presentations:
Симметрия в нашей жизни
1.
2.
Целью нашей работы являетсяизучение многообразия симметрии
и её роль в жизни.
3.
Дать понятие симметрииДоказать, что нас окружают симметричные
предметы
Определить значение использования
симметрии.
Для решения поставленных задач мы должны
провести исследования.
Рассмотреть найденные виды симметрии
Изучить внешний вид животных ,растений,
зданий и т.д
Показать симметрию в жизни человека.
4.
В наше время, наверное, трудно найти человека,который не имел бы какого-либо представления
о симметрии. Мир, в котором мы живем,
наполнен симметрией домов и улиц, гор и полей
,творениями природы и человека. С симметрией
мы встречаемся буквально на каждом шагу.
Понятие симметрии проходит через всю
многовековую историю человека. Издавна
человек использовал симметрию в архитектуре
.Древнем храмам, пирамидам, замкам, башням и
т.д.
В настоящие время ученые расширяют свои
учения о симметрии. Добавляя новые обширные
разделы. Значит выбранная мною тема
актуальна.
5.
Симметрия- соразмерность ,одинаковость в расположении частей
чего–нибудь по противоположным
сторонам от точки, прямой или
плоскости.
(Толковый словарь Ожегова)
Итак, геометрический объект
считается симметричными, если с
ним можно сделать что-то такое,
после чего он останется
неизменным
6.
Симметрия веками оставалась тем свойством,которое занимало умы философов, астрономов,
математиков, художников, архитекторов и
физиков. Древние греки были просто одержимы
ею, и даже сегодня мы, как правило, стараемся
применять симметрию во всем: от того, как мы
располагаем мебель, до того, как мы укладываем
наши волосы.
Никто не знает, почему это явление настолько
сильно занимает наши умы, или почему
математики стараются увидеть порядок и
симметрию в окружающих нас вещах – как бы то
ни было, ниже представлены примеров того, что
симметрия действительно существует, а также
того, что мы ею окружены.
Примите во внимание: как только вы об этом
задумаетесь, вы уже постоянно будете невольно
искать симметрию в окружающих вас предметах.
7.
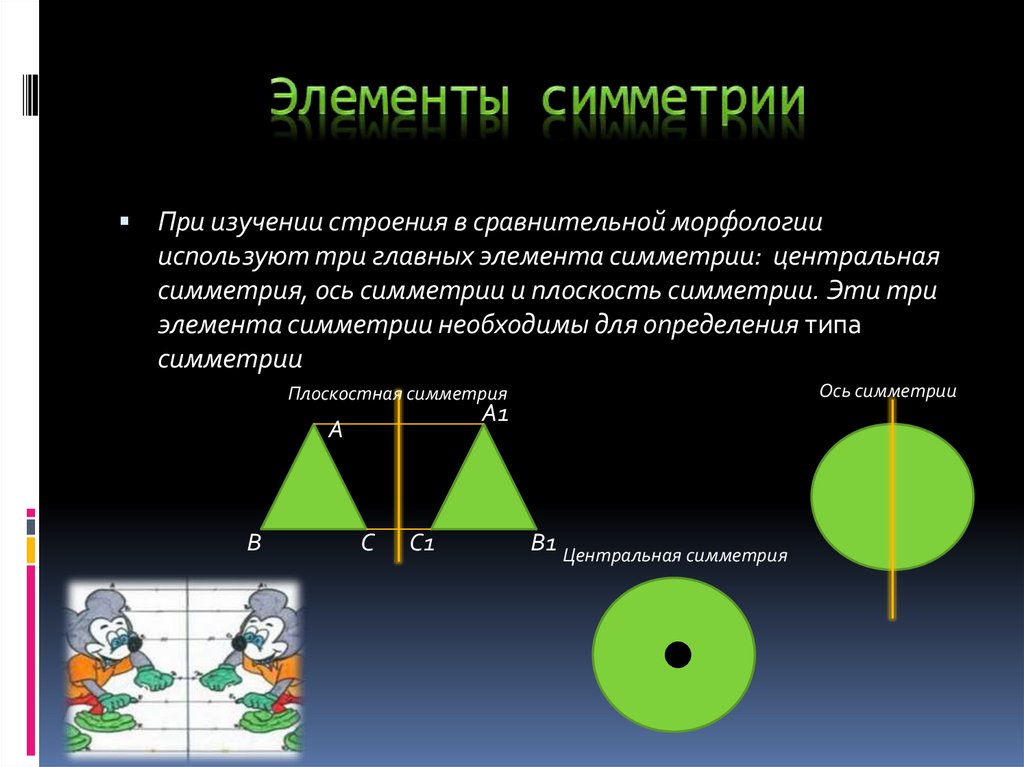
При изучении строения в сравнительной морфологиииспользуют три главных элемента симметрии: центральная
симметрия, ось симметрии и плоскость симметрии. Эти три
элемента симметрии необходимы для определения типа
симметрии
Ось симметрии
Плоскостная симметрия
А1
А
В
С
С1
В1 Центральная симметрия
О
8.
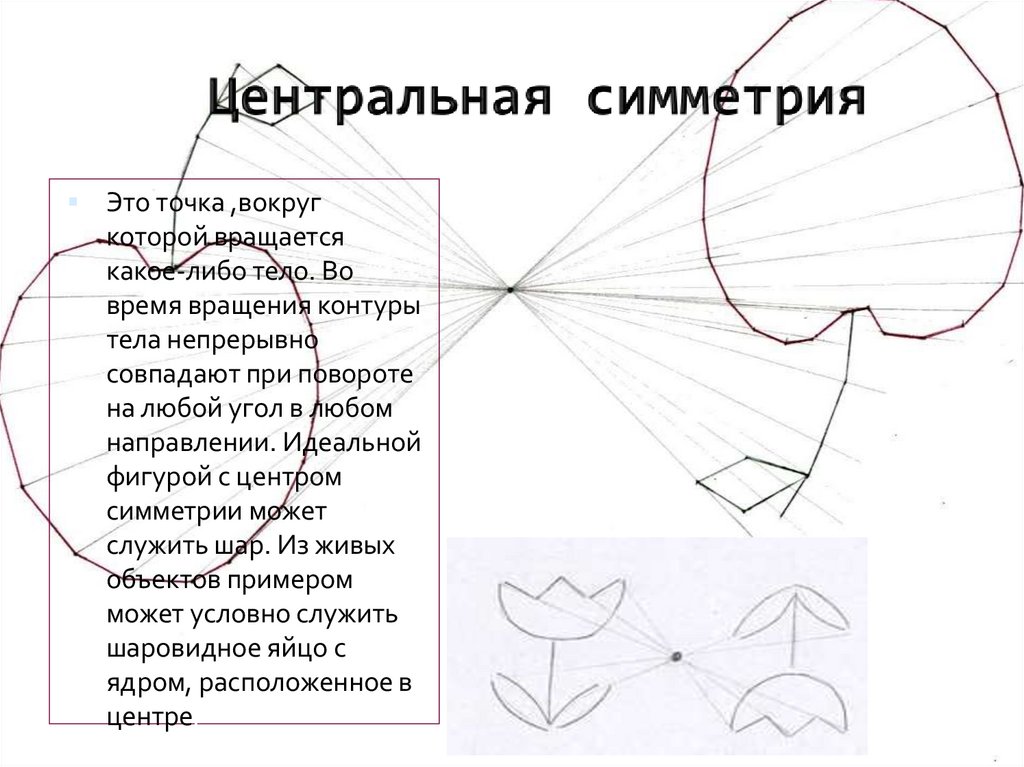
Это точка ,вокругкоторой вращается
какое-либо тело. Во
время вращения контуры
тела непрерывно
совпадают при повороте
на любой угол в любом
направлении. Идеальной
фигурой с центром
симметрии может
служить шар. Из живых
объектов примером
может условно служить
шаровидное яйцо с
ядром, расположенное в
центре.
9.
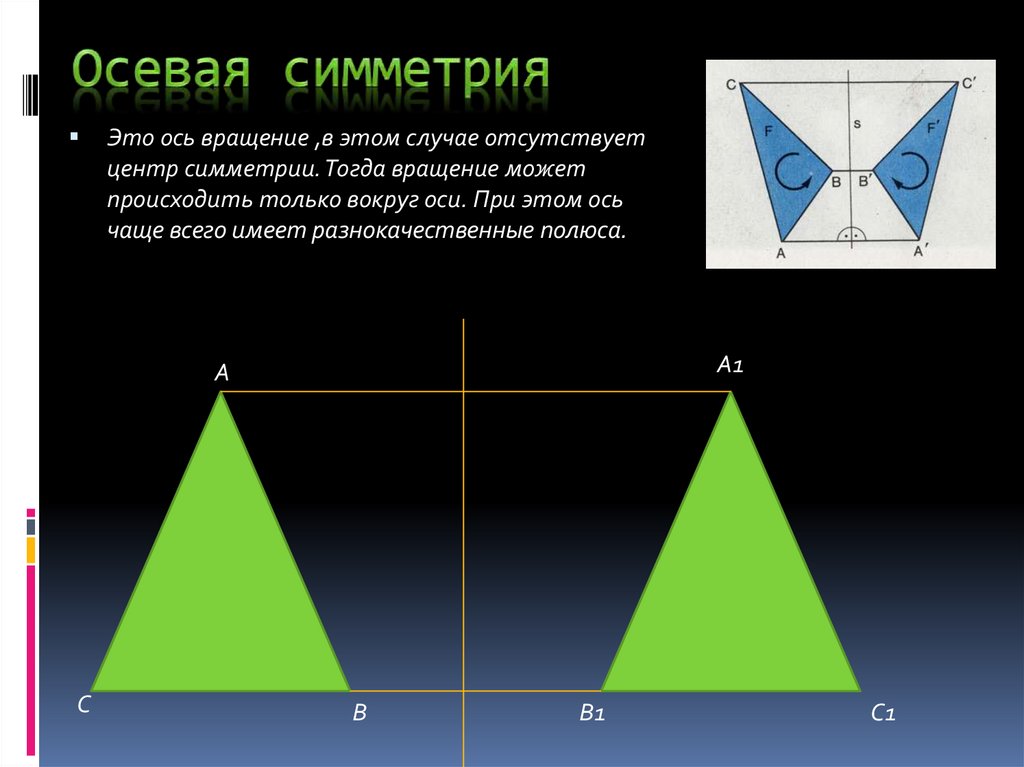
Это ось вращение ,в этом случае отсутствуетцентр симметрии. Тогда вращение может
происходить только вокруг оси. При этом ось
чаще всего имеет разнокачественные полюса.
А1
А
С
В
В1
С1
10.
Это плоскостьа
, проходящая
через ось
симметрии,
совпадающая с
ней и
рассекающая
тело на две
зеркальные
половины. Эти
половины,
расположенные
друг против
друга,
называют
антимерами
11.
Тело(или фигура)обладает симметрией вращения ,если при поворотена угол 360 градусов/n где n целое число, около некоторой прямой (ось
симметрии) оно полностью совмещается со своим исходным
положением.
Радиальная симметрии- форма симметрии, сохраняющаяся при
вращении объекта вокруг определенной точки или прямой. Часто эта
точка совпадает с центром тяжести объекта , то есть той точкой,
в которой пересекается бесконечное количество осей симметрии.
Подобными объектами могут быть шар, круг, цилиндр или конус.
12.
Зеркальная симметрия-движение пространства, множествонеподвижных точек которого является гиперплоскость.
Термин зеркальная симметрия употребляется также для описания
соответствующего типа симметрии объекта, то есть, когда объект при
операции отражения переходит в себя.
13.
Существует много других видов симметрии , имеющих абстрактный характер.Например:
Перестановочная симметрия, которая состоит в том, что если тождественные
частицы поменять местами, то никаких изменений не происходит;
Калибровочная симметрия связаны с изменением масштаба. В неживой природе
симметрия прежде всего возникает в таком явлении природы , как кристаллы, из
которых состоят практически все твердые тела. Именно она и определяет их
свойства. Самый очевидный пример красоты и совершенства кристаллов- это
известная всем снежинка.
14.
С симметрией мы встречаемся везде: в природе, технике,искусстве, науке. Понятие симметрии проходит через
всю многовековую историю человеческого творчества.
Принципы симметрии играют важную роль в физике и
математике, химии и биологии, технике и архитектуре,
живописи и скульптуре, поэзии и музыке. Законы природы
также подчитываются принципам симметрии
15.
Многие цветы обладают интереснымсвойством: их можно повернуть так, что
каждый лепесток займет положение
соседнего, цветок же совместится с
самим собой. Такой цветок обладает осью
симметрии.
Винтовая симметрия наблюдается в
расположении листьев на стеблях
большинства растений. Располагаясь
винтом по стеблю, листьев как бы
раскидывается во все стороны и не
заслоняет друг друга от света, крайне
необходимого для жизни растений.
Билатеральной симметрией обладает
также органы растений, например, стебли
многих кактусов. В ботанике часто
встречаются радиально симметрично
построенные цветы.
16.
Под симметрией уживотных понимают
соответствие в размерах,
форме и очертаниях, а
также относительное
расположение частей
тела, находящихся на
противоположных
сторонах разделяющей
линии.
Основными типами
симметрии является
радиальная(лучевая)-ей
обладает иглокожие,
кишечнополостные, медузы
и др.; или
билатериальная(двусторо
нняя)- можно сказать, что
каждое животное(Будь то Сферическая симметрия имеет место у
насекомое, рыба или птица)
радиолярий и солнечников. Любая
состоит из двух половинплоскость, проведенная через центр,
правой и левой.
делит животное на одинаковые половинки
17.
Как мы уже видели, симметрия и математические узоры существуют повсюду, кудабы мы ни посмотрели – но ограничены ли эти законы природы только нашей
планетой? По всей видимости – нет. Недавно обнаружив новую часть Млечного Пути,
астрономы считают, что наша галактика является почти совершенным отражением
самой себя. Основываясь на новой информации, учёные получили подтверждение
своей теории о том, что в нашей галактике есть только два огромных рукава: Персей
и Рукав Центавра.
В дополнение к зеркальной симметрии, Млечный Путь обладает ещё одним
удивительным дизайном – похожим на раковины наутилуса и подсолнуха, где
каждый рукав галактики представляет собой логарифмическую спираль, берущую
начало в центре галактики и расширяющуюся к внешнему краю.
18.
19.
Существует примерно 5 000 видов пауков-кругопрядов, и все они создаютпрактически совершенно круглые паутины с почти равноудаленными
радиальными опорами, исходящими из центра и связанными по спирали для
более эффективной ловли добычи. Ученые до сих пор не нашли ответа на вопрос,
почему пауки-кругопряды делают такой большой акцент на геометрию, так как
исследования показали, что округлая паутина не удерживает добычу лучше, чем
паутина неправильной формы.
Некоторые ученые предполагают, что пауки строят круглые паутины из-за того,
что они более прочные, и радиальная симметрия помогает равномерно
распределить силу удара, когда жертва попадает в сети, в результате чего в
паутине оказывается меньше разрывов. Но остается вопрос: если это
действительно лучший способ создания паутины, то почему не все пауки его
используют? У некоторых пауков, не являющихся кругопрядами, есть
возможность создавать такую же паутину, однако они этого не делают.
Например, недавно обнаруженный в Перу паук строит отдельные части сети
одинакового размера и длины (что доказывает его способность «замерять»), но
затем он просто соединяет все эти части одинакового размера в случайном
порядке в большую паутину, которая не обладает какой-то определённой
формой. Может быть эти пауки из Перу знают что-то, чего не знают паукикругопряды, или же они ещё просто не оценили всю прелесть симметрии?
20.
Большинство животныхобладает двусторонней
симметрией, это означает,
что их можно разделить на
две одинаковые половины,
если линию деления
провести по их центру тела.
Даже люди обладают
двусторонней симметрией,
и некоторые учёные
считают, что симметрия
человека является самым
важным фактором.
21.
Помимо растений существуют также некоторыеживотные, демонстрирующие собою числа
Фибоначчи. Например, раковина Наутилуса
выросла в «Спираль Фибоначчи». Спираль
образуется в результате попытки раковины
поддерживать ту же пропорциональную форму по
мере своего роста наружу. В случае наутилуса,
такая тенденция роста позволяет ему сохранять
одинаковую форму тела в течение всей своей
жизни (в отличие от людей, чьи тела изменяют
свои пропорции по мере взросления).
Как и следовало бы ожидать – в этом правиле
существуют и исключения: не каждая раковина
наутилуса вырастает в спираль Фибоначчи. Но все
они растут в виде своеобразных
логарифмических спиралей. И, до того как вы
начнёте задумываться над тем, что эти
головоногие, пожалуй, знают математику лучше
вас, помните, что их раковины растут в такой
форме неосознанно для них, и что они просто
пользуются эволюционным дизайном, который
позволяет моллюску расти, не изменяя форму.
22.
Пчёлы это не только ведущие производителимёда – они также знают толк в геометрии. Тысячи
лет люди поражались совершенству
гексагональных форм в медовых сотах и
задавались вопросом о том, как же пчёлы могут
инстинктивно создавать такие формы, которые
человек может создавать только с линейкой и
компасом. Медовые соты являются предметов
обойной симметрии, где повторяющийся узор
покрывает плоскость (например, плиточный пол
или мозаика).
Так каким же образом и почему пчёлы так любят
строить шестиугольники? Начнём с того, что
математики считают, что эта совершенная форма
позволяет пчёлам запасать самое большое
количество мёда, используя наименьшее
количество воска. При строительстве других
форм у пчёл получались бы большие
пространства, так как такие фигуры, как
например круг – не прилегают друг к другу
полностью.
Другие наблюдатели, которые менее склонны
верить в сообразительность пчёл, считают, что
они формируют гексагональную форму
совершенно «случайно». Другими словами,
пчёлы на самом деле делают круги, а воск сам по
себе принимает гексагональную форму. В любом
случае – это произведение природы и довольнотаки потрясающее.
23.
Симметрия сооружений связывается с организацией его функций. Проекция плоскостисимметрии -ось здания- определяет обычно размещение главного входа и начало основных
потоков движения.
Каждая деталь в симметричной системе существует как двойник своей обязательной паре,
расположенной по другую сторону оси, и благодаря этому она может рассматриваться лишь как
часть целого.
Наиболее распространена в архитектуре зеркальная симметрия. Ей подчинены постройки
Древнего Египта и храмы античной Греции, амфитеатры, термы, базилики и триумфальные арки
римлян, дворцы и церкви Ренессанса, равно как и многочисленные сооружения современной
архитектуры.
24.
Никто не усомнился , что внешне человек построен симметрично:левой руке всегда соответствует правая и обе руки совершенно
одинаковы. Но сходство между нашими руками, ушами, глазами и
другими частями тела такое же ,как между предметом и его
отражением в зеркале.
25.
Многочисленные измерения параметров лица у мужчин и женщинпоказали,что правая его половина по сравнению с левой, имеет более
выраженные поперечные размеры, что придает лицу более грубые черты,
присущие мужскому полу.Левая половина лица имеет более выраженные
продольные размеры, что придает ему плавность линий и
женственность.Этот факт объясняет преимущественное желание лиц
женского пола позировать перед художниками левой стороной лица, а лиц
мужского пола правой.
26.
Полидром(от гр.Polindromos-бегущий обратно)-это некоторыйобъект, в который задана симметрия составляющих от начала к
концу и от конца к началу. Например, фразу или текст.
Прямой текст палиндрома, читающийся в соответствии с
нормальным направлением чтения в данной письменности
(обычно слева направо), называется прямоходным, обратныйракоходным или реверсом(справа налево). Некоторые числа
также обладают симметрией.
27.
В ходе исследования мырассмотрели
Понятие симметрии
Виды симметрии
Симметрия в природе
Симметрия животных и
растений
Симметрия в архитектуре
Симметрия человеке
Симметрия в нашей речи
Исследования, проведенные нами , показали , что симметрия является
одним из принципов гармонического состояния мира .Симметрия поистине
безгранична. Всюду она определяет гармонию природы, мудрость науки и
красоту. Симметрию можно рассматривать еще долгое время ,потому что она
присутствует и в прошлом и в будущем.Это не только математическое
понятие , а ещё наша жизнь .
28.
1. Афанасьев А. Н, Мифология Древней Руси. –М.: Эксмо, 2006.
2. Вейль Г. Симметрия. – Изд. 2-е, стер. – М.:
Единториал УРСС, 2003.
3. tecrussia.ru›stati…krasote…zdorove/749simmetriya…
4.Бахман Ф., Построение геометрии на основе
понятия симметрии-Наука,1969.
5. wowfacts.net›tag/fakty-o-simmetrii/
6. ru.wikipedia.org›Симметрия
7. otherreferats.allbest.ru›Биология и
естествознание›00142212_0.htm
























 mathematics
mathematics








