Что такое стереометрия? 10 класс

1. ЧТО ТАКОЕ СТЕРЕОМЕТРИЯ 10 КЛАСС

2. Содержание

1.
Предмет стереометрии
2.
Многоугольник
3.
Призма
4.
Параллелепипед
5.
Объем тела
6.
Свойства прямоугольного параллелепипеда
7.
Пирамида

3.

8. Цилиндр
9. Конус
10. Сфера и шар
11. О себе
12.Задачи

4. Предмет стереометрии

До сих пор мы занимались планиметрией- изучали
свойства плоских геометрических фигур, т.е. фигур,
целиком расположенных в некоторой плоскости. Но
окружающие нас предметы в большинстве своем не
являются плоскими, они расположены в пространстве
и не умещаются в какой-то одной плоскости.

5.

Любой реальный предмет занимает какую-то часть пространства. Раздел
геометрии, в котором изучаются свойства фигур в пространстве,
называется стереометрией. Это слово происходит от греческих слов
«стерео» - объемный, пространственный и «метрео» -измерять.
В стереометрии наряду с простейшими фигурами – точками, прямыми и
плоскостями рассматриваются геометрические тела и их поверхности.

6.

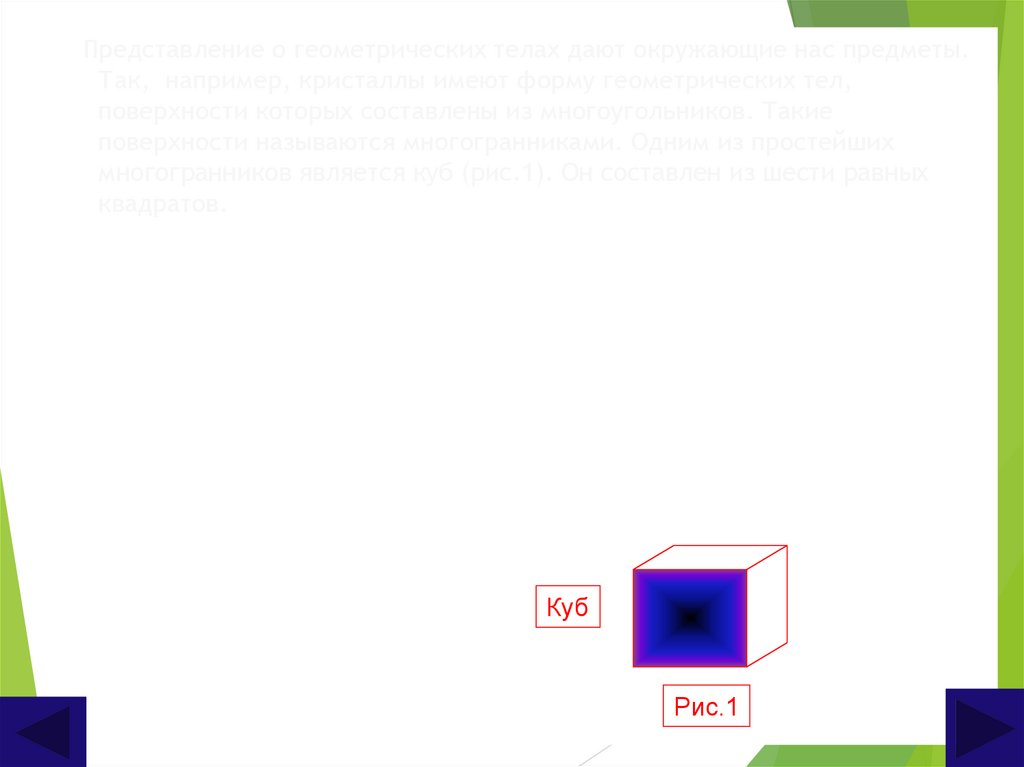
Представление о геометрических телах дают окружающие нас предметы.
Так, например, кристаллы имеют форму геометрических тел,
поверхности которых составлены из многоугольников. Такие
поверхности называются многогранниками. Одним из простейших
многогранников является куб (рис.1). Он составлен из шести равных
квадратов.
Куб
Рис.1

7.

Капли жидкости в невесомости принимают форму геометрического тела,
называемого шаром (рис.2). Такую же форму имеет футбольный мяч.
Консервная банка имеет форму геометрического тела, называемого
цилиндром (рис.3).
Шар
Рис.2
Цилиндр
Рис.3

8.

В отличие от реальных предметов геометрические тела, как и всякие
геометрические фигуры, являются воображаемыми объектами. Мы
представляем геометрическое тело как часть пространства,
отделенную от остальной части пространства поверхностью – границей
этого тела. Так, например, граница шара есть сфера, а граница
цилиндра состоит из двух кругов – оснований цилиндра и боковой
поверхности.

9.

Плоскость, по обе стороны от которой имеются точки данного тела,
называется секущей плоскостью этого тела. Фигура, которая образуется
при пересечении тела с секущей плоскостью (т.е. общая часть тела и
секущей плоскости), называется сечением тела. Так, например,
сечением шара является круг.

10.

При изучении пространственных фигур, в частности геометрических тел,
пользуются их изображениями на чертеже. Как правило, изображением
пространственной фигуры служит ее проекция на ту или иную
плоскость. Одна и та же фигура допускает различные изображения.
Обычно выбирают то из них, которое создает правильное
представление о форме фигуры и наиболее удобно для исследования
ее свойств.

11.

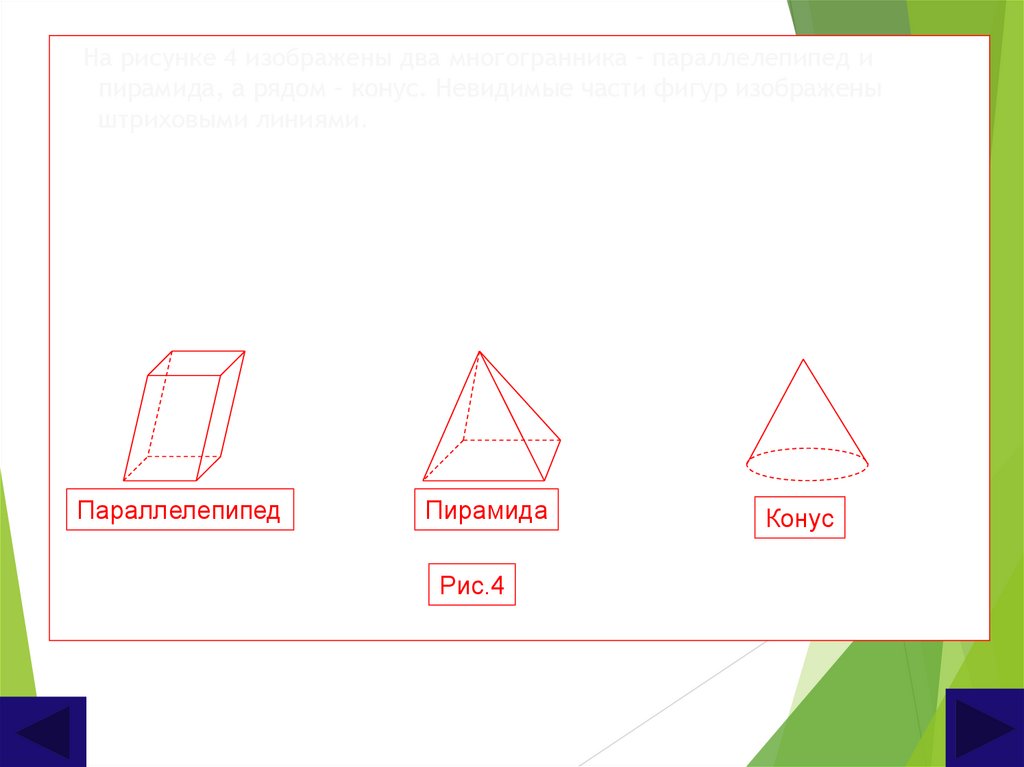
На рисунке 4 изображены два многогранника – параллелепипед и
пирамида, а рядом – конус. Невидимые части фигур изображены
штриховыми линиями.
Параллелепипед
Пирамида
Рис.4
Конус

12.

В этой главе мы рассмотрим некоторые виды многогранников и тела
вращения – цилиндр, конус, шар, приведем формулы, по которым
вычисляются их объемы и площади поверхностей. При этом мы будем
опираться в основном на наглядные представления.

13. Многогранник

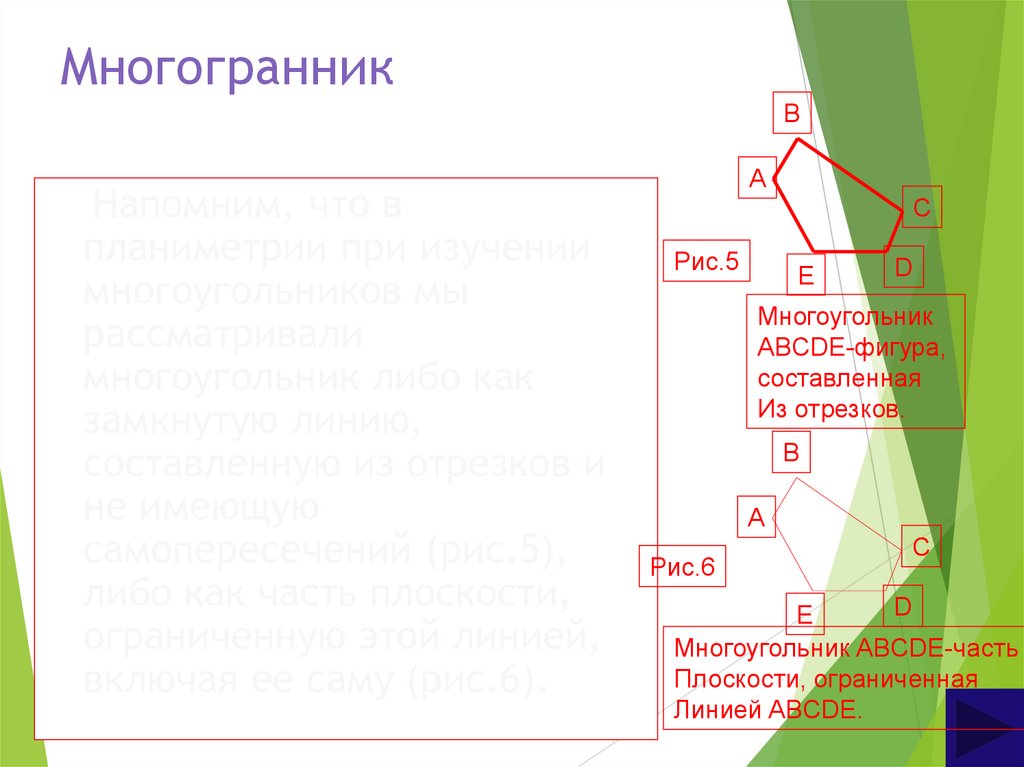
В
Напомним, что в
планиметрии при изучении
многоугольников мы
рассматривали
многоугольник либо как
замкнутую линию,
составленную из отрезков и
не имеющую
самопересечений (рис.5),
либо как часть плоскости,
ограниченную этой линией,
включая ее саму (рис.6).
А
C
Рис.5
Е
D
Многоугольник
ABCDЕ-фигура,
составленная
Из отрезков.
В
А
Рис.6
C
D
Е
Многоугольник ABCDЕ-часть
Плоскости, ограниченная
Линией ABCDЕ.

14.

С одним из самых простых
многогранников –
прямоугольным
параллелепипедом – вы
знакомы давно. Этот
многогранник составлен из
шести прямоугольников
(рис.7). Форму
прямоугольного
параллелепипеда имеют
коробки, комнаты и многие
другие предметы. На рисунках
8-10 изображены другие
многогранники: куб (это
прямоугольный
параллелепипед,
составленный из шести
равных квадратов), тетраэдр,
октаэдр.
M
Рис.7
N
Прямоугольный
параллелепипед
Рис.8
Куб
Рис.9
Тетраэдр
Рис.10
Октаэдр

15.

Можно сказать, что многогранник – это поверхность, составленная из
многоугольников и ограничивающая некоторое геометрическое тело. Это
тело также называется многогранником. Тетраэдр и октаэдр (рис. 9, 10)
составлены соответственно
из четырех и восьми
треугольников, что
отражено в названии
этих многогранников:
по гречески «тетра» четыре, а «окто» - восемь.
Рис.9
Тетраэдр
Рис.10
Октаэдр

16.

Многоугольники, из которых составлен многогранник, называется его
гранями. При этом предполагается, что никакие две соседние грани
многогранника не лежат в одной плоскости. Гранями прямоугольного
параллелепипеда являются прямоугольники, а гранями тетраэдра и
октаэдра – треугольники. Стороны граней называются ребрами, а концы
ребер – вершинами многогранника. Отрезок, соединяющий две
вершины, не принадлежащие одной грани, называется диагональю
многогранника.

17.

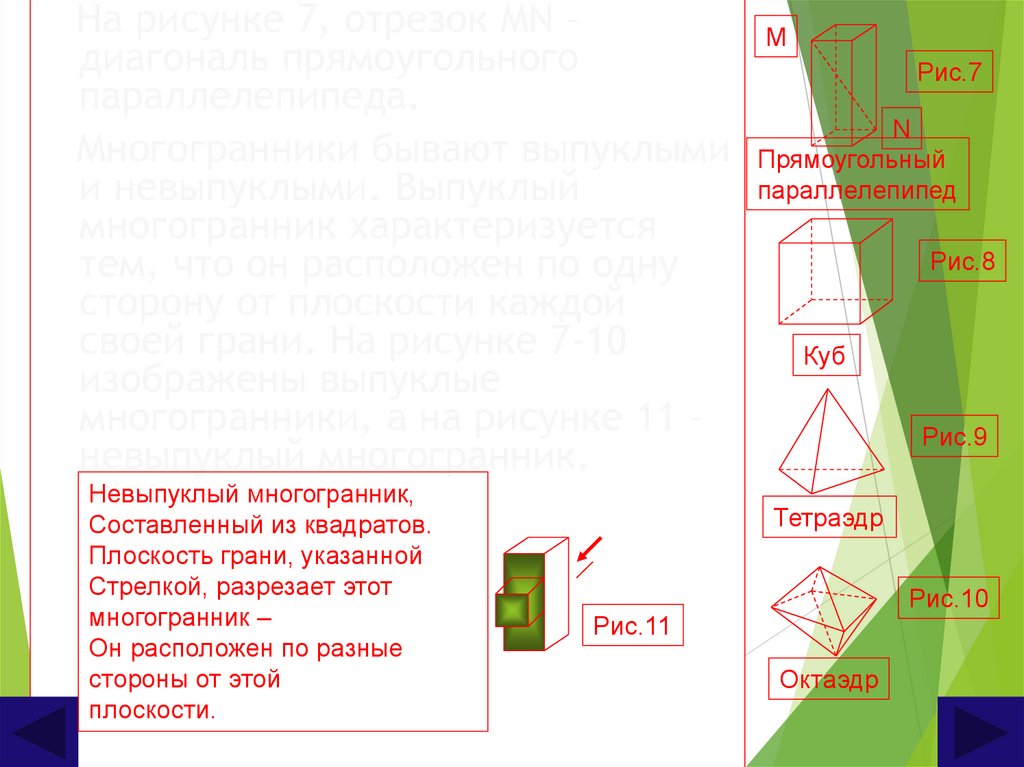
На рисунке 7, отрезок MN –
диагональ прямоугольного
параллелепипеда.
Многогранники бывают выпуклыми
и невыпуклыми. Выпуклый
многогранник характеризуется
тем, что он расположен по одну
сторону от плоскости каждой
своей грани. На рисунке 7-10
изображены выпуклые
многогранники, а на рисунке 11 –
невыпуклый многогранник.
Невыпуклый многогранник,
Составленный из квадратов.
Плоскость грани, указанной
Стрелкой, разрезает этот
многогранник –
Он расположен по разные
стороны от этой
плоскости.
M
Рис.7
N
Прямоугольный
параллелепипед
Рис.8
Куб
Рис.9
Тетраэдр
Рис.10
Рис.11
Октаэдр

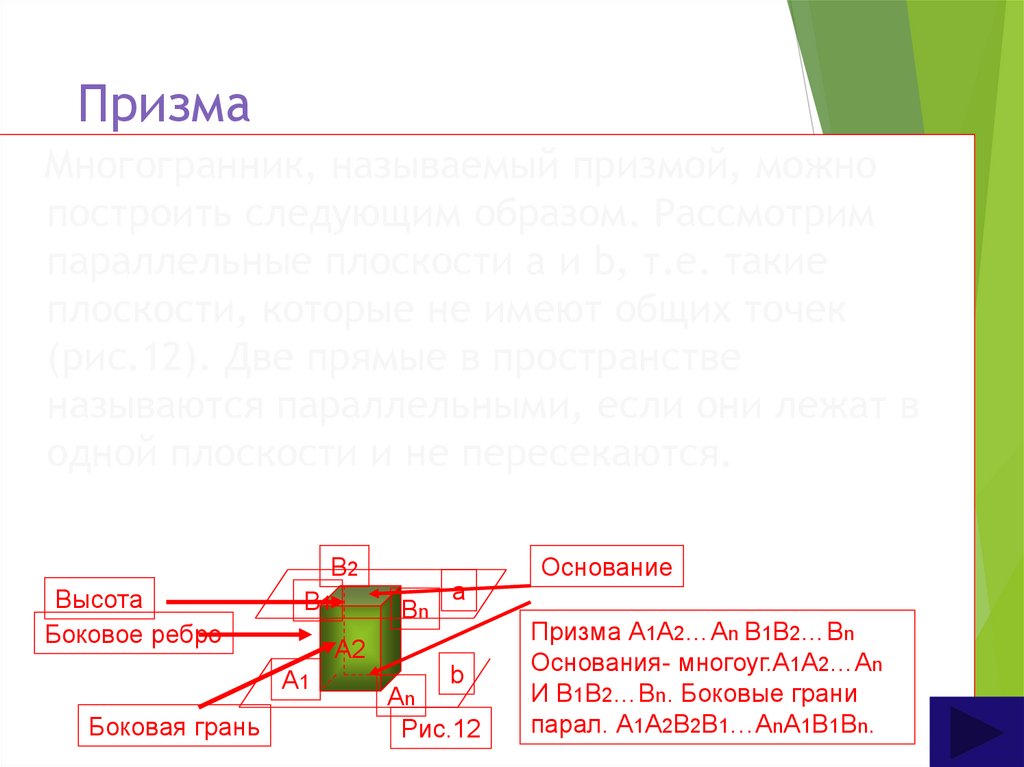
18. Призма

Многогранник, называемый призмой, можно
построить следующим образом. Рассмотрим
параллельные плоскости a и b, т.е. такие
плоскости, которые не имеют общих точек
(рис.12). Две прямые в пространстве
называются параллельными, если они лежат в
одной плоскости и не пересекаются.
Основание
B2
Высота
Боковое ребро
B1
a
A2
A1
Боковая грань
Bn
b
An
Рис.12
Призма А1А2…Аn В1В2…Вn
Основания- многоуг.А1А2…Аn
И В1В2…Вn. Боковые грани
парал. А1А2В2В1…АnА1В1Вn.

19.

Призмы бывают прямыми и наклонными.
Чтобы дать определение прямой призмы,
введем понятие перпендикулярности
прямой и плоскости. Прямая а,
пересекающая плоскость а в некоторой
точке Н (рис.13), называется
перпендикулярной к этой плоскости, если
она перпендикулярна к любой прямой,
лежащей в плоскости а и проходящей
а
через точку Н. Перпендикулярность
прямой а и плоскости а
Н
а
обозначается так: а а
а а
Рис.13

20.

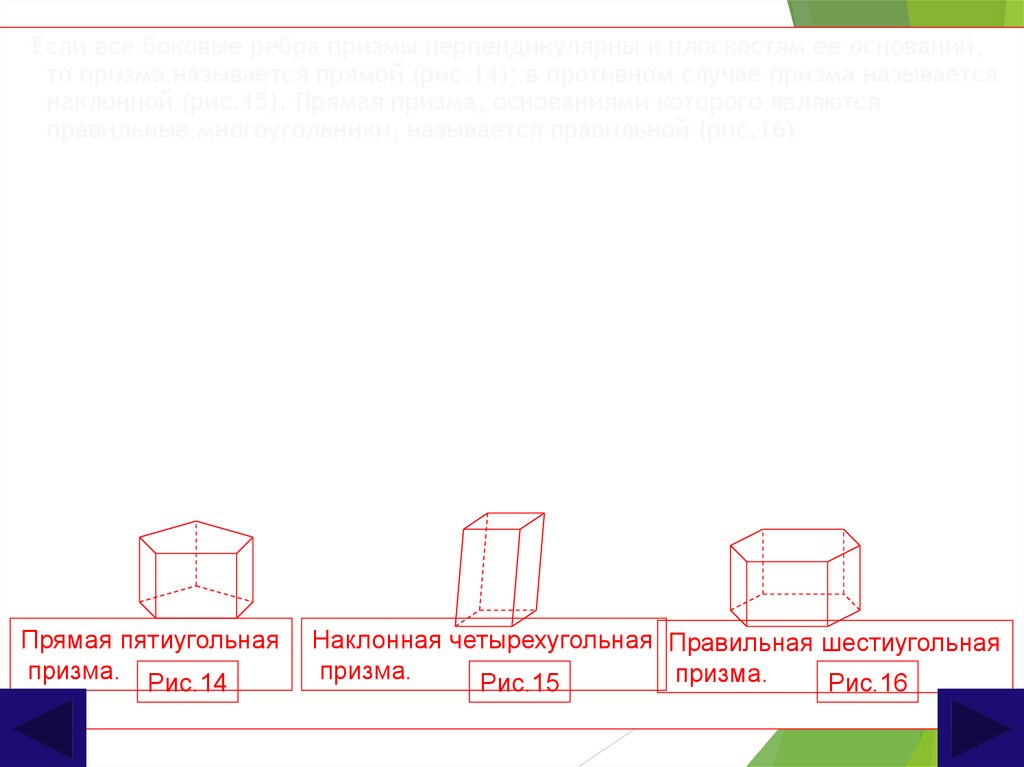
Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований,
то призма называется прямой (рис.14); в противном случае призма называется
наклонной (рис.15). Прямая призма, основаниями которого являются
правильные многоугольники, называется правильной (рис.16).
Прямая пятиугольная
призма. Рис.14
Наклонная четырехугольная Правильная шестиугольная
призма.
призма.
Рис.15
Рис.16

21. Параллелепипед

Четырехугольная призма, основаниями которой являются
параллелепипедом (рис.17). Все шесть граней параллелепипеда –
параллелограмм.
Если параллелепипед прямой, т.е. его боковые ребра перпендикулярны
к плоскостям оснований, то боковые грани – прямоугольники.
Параллелепипед
Рис.17

22.

Если же и основаниями прямого параллелепипеда служат
прямоугольники, то этот параллелепипед – прямоугольный.
Мы знаем, что диагонали параллелограмма пересекаются и точкой
пересечения делятся пополам. Оказывается, что аналогичным
свойством обладают диагонали параллелепипеда.

23.

Четыре диагонали параллелепипеда пересекаются в одной точке и
делятся этой точкой пополам.
Доказательство этого утверждения основано на следующем факте: если
две прямые в пространстве параллельны третьей прямой, то они
параллельны. В этом случае, когда все три прямые лежат в одной
плоскости.

24. Объем тела

Понятие объема тела вводится по аналогии понятием
площади плоской фигуры. Как мы помним, каждый
многоугольник имеет площадь, которая измеряется с
помощью выбранной единицы измерения площадей.
В качестве единицы измерения площадей обычно
берут квадрат, сторона которого равна единице
измерения отрезков.

25.

Так же будем считать, что каждое из рассмотренных нами тел имеет
объем, который можно измерить с помощью выбранной единицы
измерения объемов. За единицу измерения объемов примем куб, ребро
которого равно единице измерения отрезков. Куб с ребром 1 см
называется кубическим сантиметром и обозначается так: 1 см.
Аналогично определяются кубический метр (м ), кубический миллиметр
(мм ) и т.д.
3
3
3

26.

Процедура измерения объемом аналогична процедуре измерения
площадей. При выбранной единице измерения объем тела выражается
положительным числом, которое показывает, сколько единиц
измерения объемов и ее частей укладываются в этом теле. Ясно, что
число, выражающее объем тела, зависит от выбора единицы измерения
объемов. Поэтому единица измерения объемов указывается после
этого числа.

27.

Например, если в качестве единицы измерения
объемов взят 1 см,3и при этом объем V
некоторого тела оказался равным 2, то пишут:
V=2см. 3
Если два тела равны, то каждое из них содержит
столько же единиц измерения объемов и ее
частей, сколько и другое тело. Таким образом,
1. Равные тела имеют равный объем.
Рассмотрим тело, составленное из нескольких
тел так, что внутренние области этих тел не
имеют общих точек (рис.18).
F
Ясно, что объем всего тела
складывается из объемов
V=VF+VQ
составляющих его тел. Итак,
Рис.18
Q

28.

2. Если тело составлено из нескольких тел, то его объем равен сумме
объемов этих тел.
Свойство 1 и 2 называются основными свойствами объемов. Напомним,
что аналогичными свойствами обладают длины отрезков и площади
многоугольников.
Для нахождения объемов тел в ряде случаев удобно пользоваться
теоремой, получивший название принцип Кавальери.

29. Свойства прямоугольного параллелепипеда

Когда мы говорим о размерах комнаты, имеющей
форму прямоугольного параллелепипеда, то обычно
употребляем слово «длина», «ширина» и «высота»,
имея в виду длины трех ребер с общей вершиной. В
геометрии эти три величины объединяются общим
названием: измерения прямоугольного
параллелепипеда.

30.

У прямоугольника два измерения – длина и ширина. При этом, как мы
знаем, квадрат диагонали прямоугольника равен сумме квадратов
двух его измерений.
Свойства:
1.
Квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трех его измерений.
2.
Площадь прямоугольника равна произведению его измерений.

31.

3.
Объем прямоугольного параллелепипеда равен произведению трех
его измерений.
4.
Объем прямоугольного параллелепипеда равен произведению
площади основания на высоту.
V=abc, V=Sh.
5.
Объем призмы равен произведению площади основания на высоту.

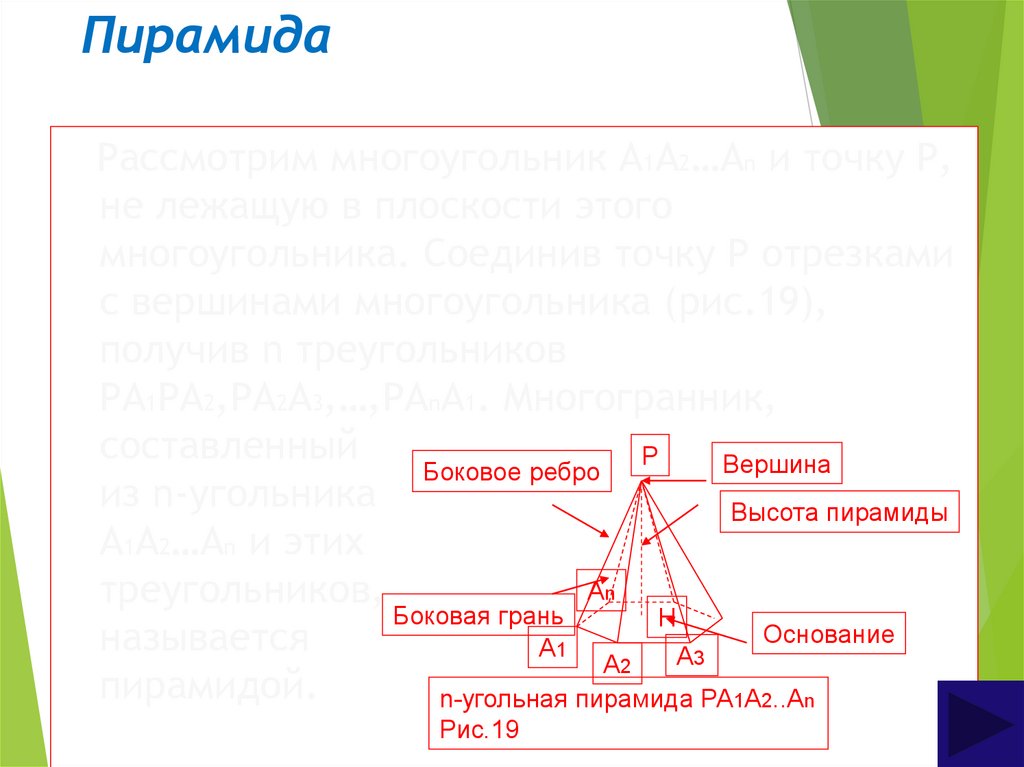
32. Пирамида

Рассмотрим многоугольник А1А2…Аn и точку Р,
не лежащую в плоскости этого
многоугольника. Соединив точку Р отрезками
с вершинами многоугольника (рис.19),
получив n треугольников
РА1РА2,РА2А3,…,РАnА1. Многогранник,
составленный
Р
Вершина
Боковое ребро
из n-угольника
Высота пирамиды
А1А2…Аn и этих
Аn
треугольников,
Боковая грань
Н
Основание
называется
А1
А3
А2
пирамидой.
n-угольная пирамида РА1А2..Аn
Рис.19

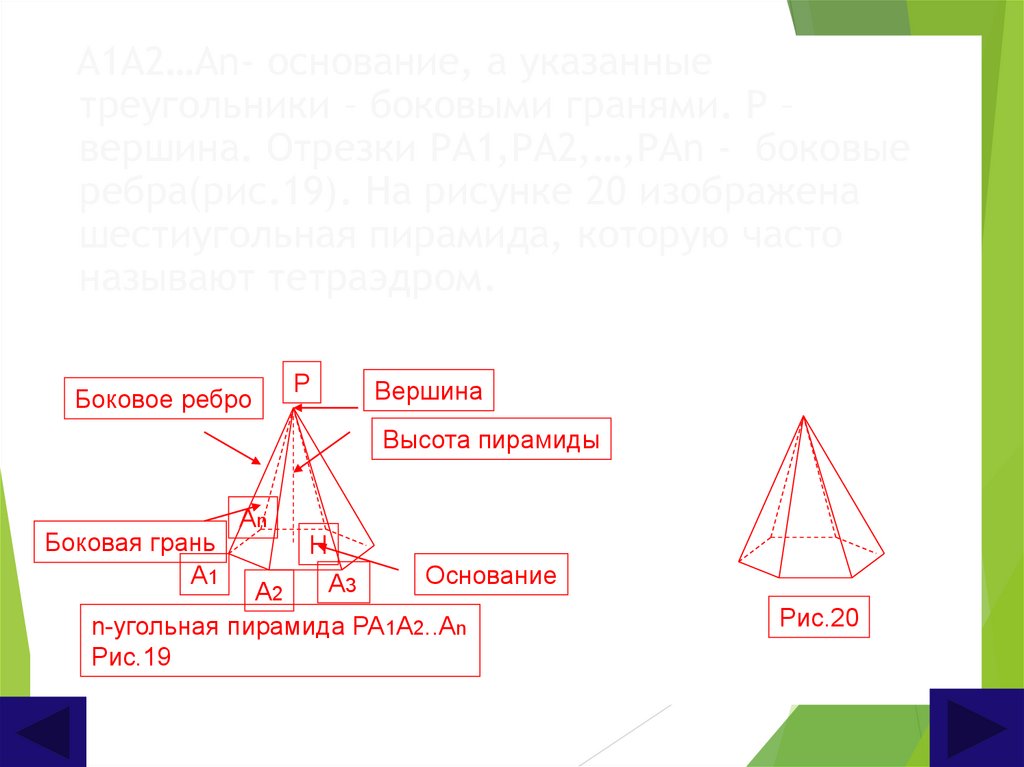
33.

А1А2…Аn- основание, а указанные
треугольники – боковыми гранями. Р –
вершина. Отрезки РА1,РА2,…,РАn - боковые
ребра(рис.19). На рисунке 20 изображена
шестиугольная пирамида, которую часто
называют тетраэдром.
Боковое ребро
Р
Вершина
Высота пирамиды
Боковая грань
А1
Аn
Н
Основание
А3
А2
n-угольная пирамида РА1А2..Аn
Рис.19
Рис.20

34.

Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и
перпендикулярный к этой плоскости, называется высотой пирамиды.
Пирамида называется правильный, если ее основания – правильный
многоугольник, а отрезок, с соединяющий вершину пирамиды с центром
основания, является ее высотой. Высотой боковой грани правильной
пирамиды, проведенная из ее вершины, называется апофемой.

35.

Объем пирамиды равен одной трети произведения площади основания
на высоту.

36. Цилиндр

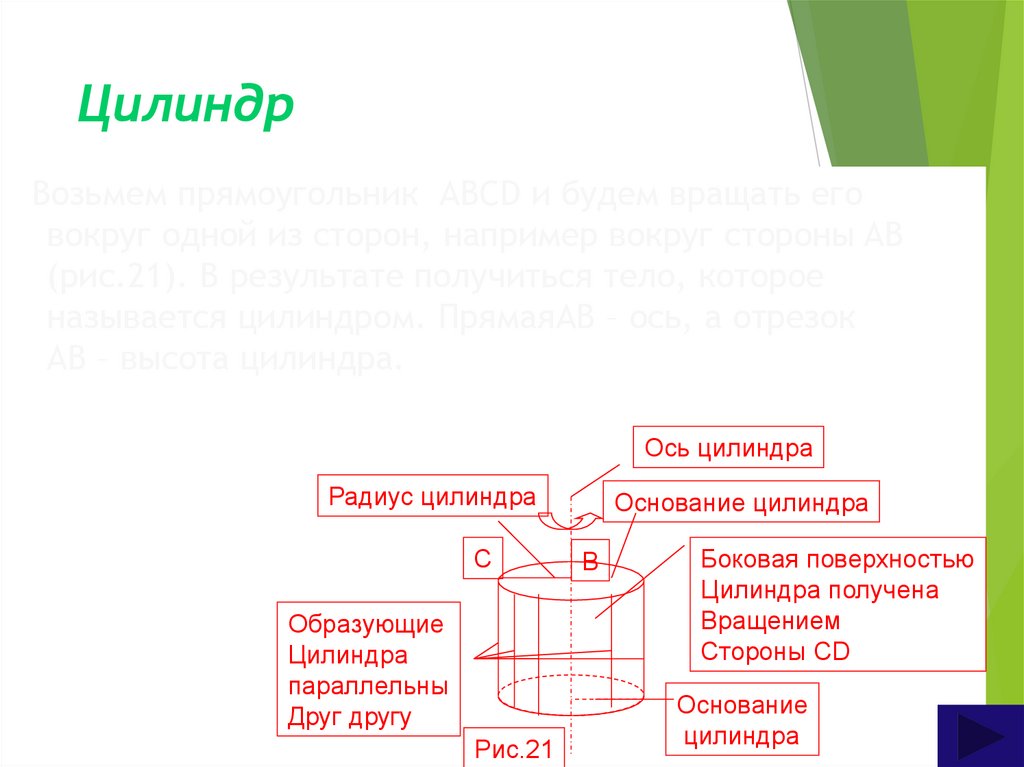
Возьмем прямоугольник АBCD и будем вращать его
вокруг одной из сторон, например вокруг стороны AB
(рис.21). В результате получиться тело, которое
называется цилиндром. ПрямаяAB – ось, а отрезок
AB – высота цилиндра.
Ось цилиндра
Радиус цилиндра
С
Образующие
Цилиндра
параллельны
Друг другу
Рис.21
Основание цилиндра
В
Боковая поверхностью
Цилиндра получена
Вращением
Стороны CD
Основание
цилиндра

37.

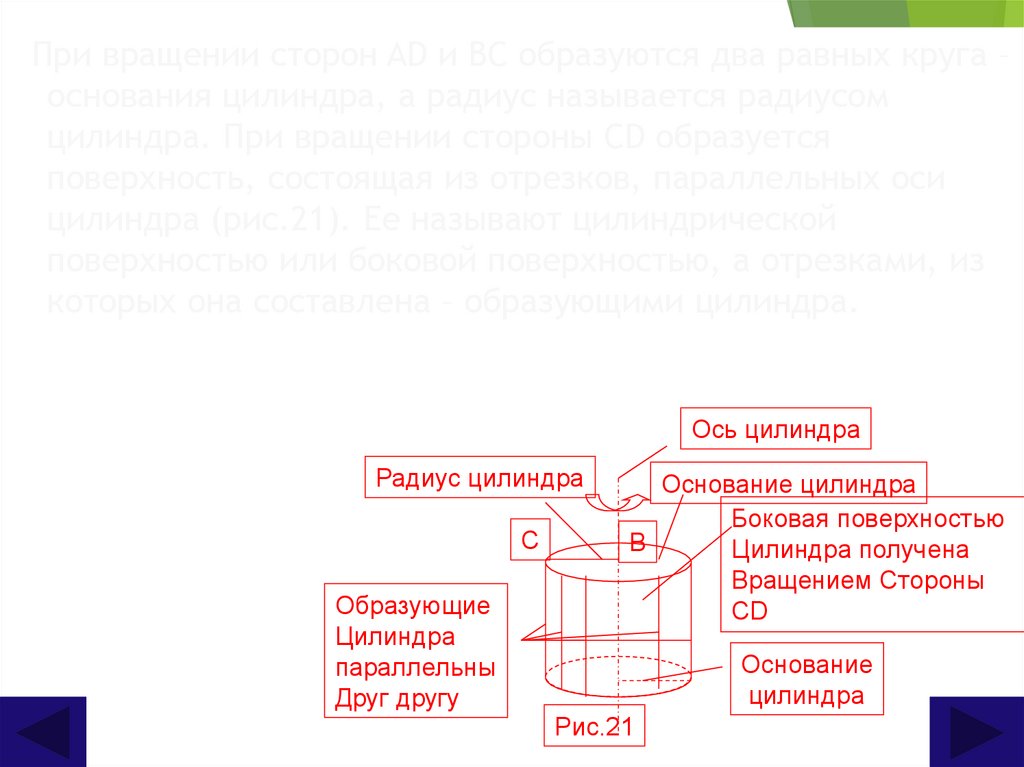
При вращении сторон AD и BC образуются два равных круга –
основания цилиндра, а радиус называется радиусом
цилиндра. При вращении стороны CD образуется
поверхность, состоящая из отрезков, параллельных оси
цилиндра (рис.21). Ее называют цилиндрической
поверхностью или боковой поверхностью, а отрезками, из
которых она составлена – образующими цилиндра.
Ось цилиндра
Радиус цилиндра
С
Образующие
Цилиндра
параллельны
Друг другу
Основание цилиндра
Боковая поверхностью
В
Цилиндра получена
Вращением Стороны
CD
Основание
цилиндра
Рис.21

38.

Таким образом, цилиндр – это тело, ограниченное двумя равными кругами
и цилиндрической поверхностью.
Объем цилиндра равен произведению площади основания на высоту.
Площадь Sбок боковой поверхности цилиндра равна площади ее
развертки, т.е. Sбок=2 пrh

39. Конус

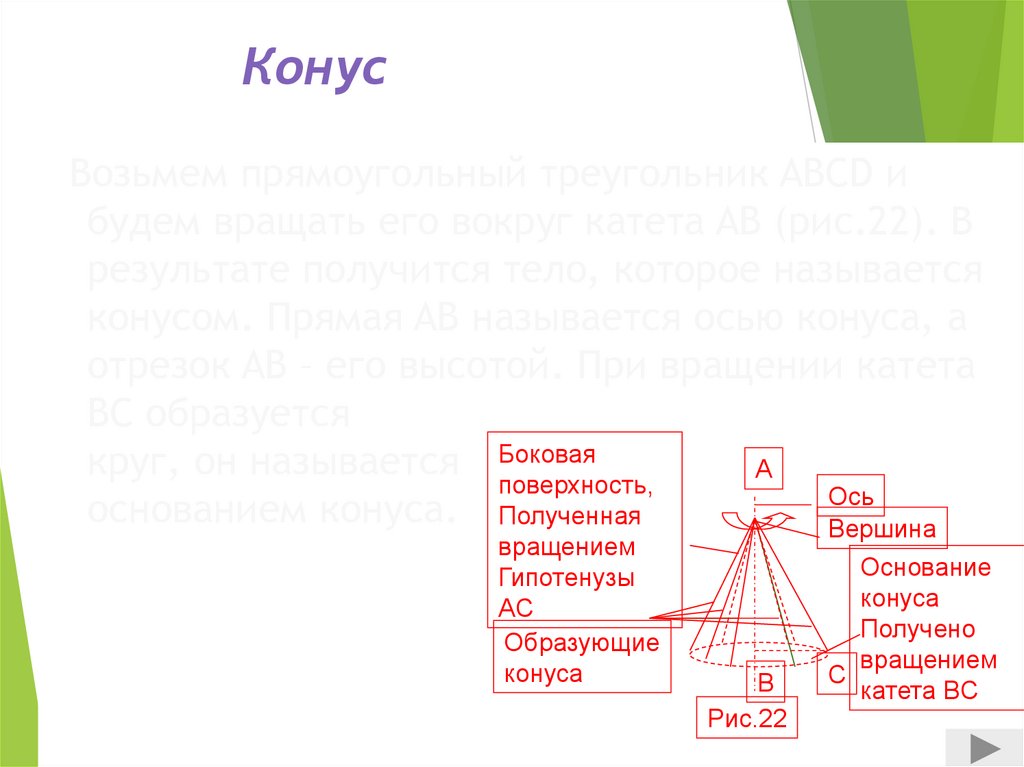
Возьмем прямоугольный треугольник ABCD и
будем вращать его вокруг катета AB (рис.22). В
результате получится тело, которое называется
конусом. Прямая AB называется осью конуса, а
отрезок AB – его высотой. При вращении катета
BC образуется
круг, он называется Боковая
А
поверхность,
Ось
основанием конуса. Полученная
Вершина
вращением
Гипотенузы
AC
Образующие
конуса
В
Рис.22
Основание
конуса
Получено
вращением
С
катета BC

40.

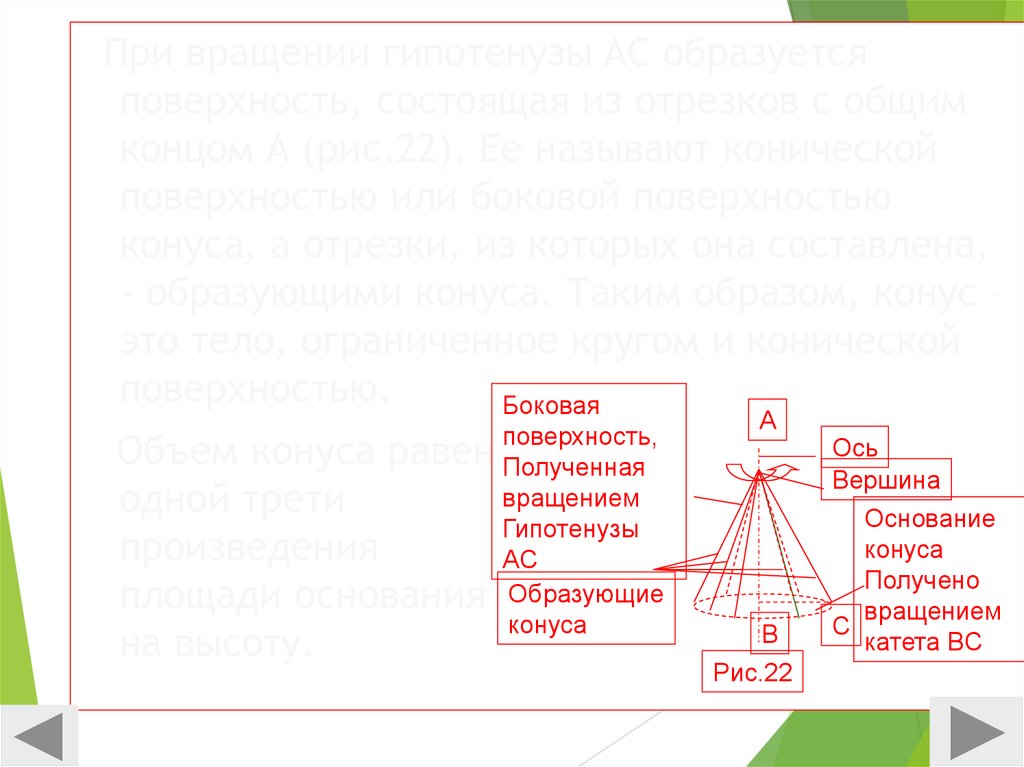
При вращении гипотенузы AC образуется
поверхность, состоящая из отрезков с общим
концом А (рис.22). Ее называют конической
поверхностью или боковой поверхностью
конуса, а отрезки, из которых она составлена,
- образующими конуса. Таким образом, конус –
это тело, ограниченное кругом и конической
поверхностью.
Боковая
Объем конуса равен поверхность,
Полученная
вращением
одной трети
Гипотенузы
произведения
AC
площади основания Образующие
конуса
на высоту.
А
В
Рис.22
Ось
Вершина
Основание
конуса
Получено
вращением
С
катета BC

41.

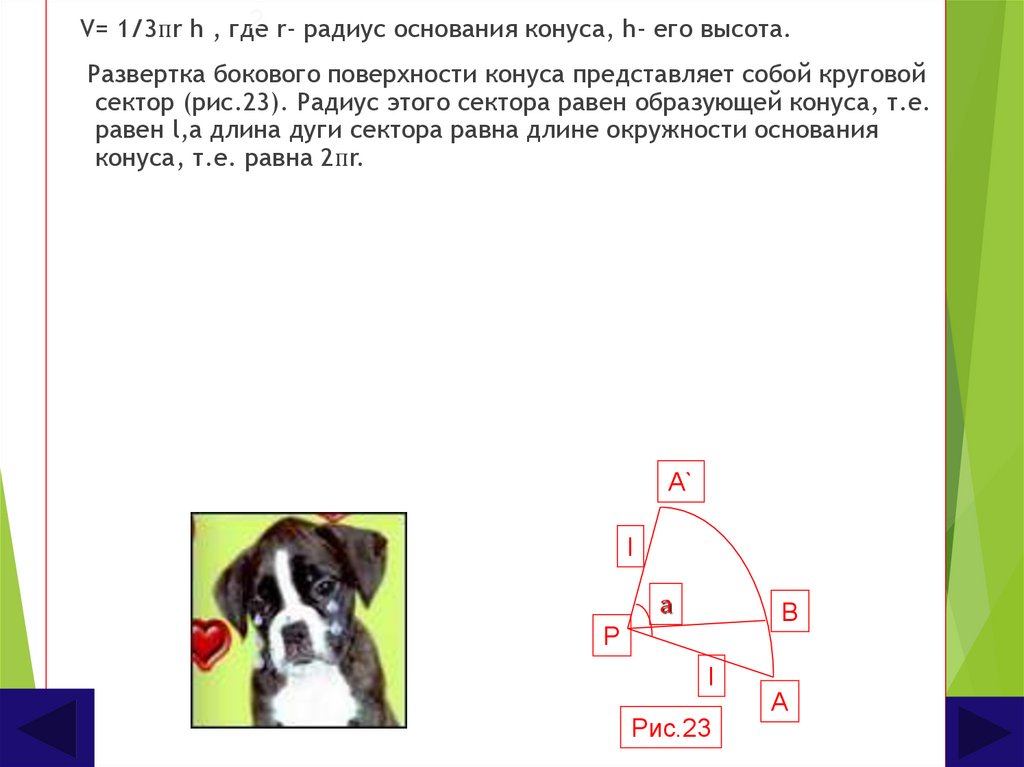
2 r- радиус основания конуса, h- его высота.
V= 1/3пr h , где
Развертка бокового поверхности конуса представляет собой круговой
сектор (рис.23). Радиус этого сектора равен образующей конуса, т.е.
равен l,а длина дуги сектора равна длине окружности основания
конуса, т.е. равна 2пr.
А`
l
а
В
P
l
Рис.23
А

42.

Площадь Sбок боковой поверхности конуса
равна площади ее развертки, т.е.
2
Sбок= пl /360*a, где а - градусная мера дуги
сектора. Длина дуги окружности с градусной
мерой а и радиусом l равна пlа/180. С другой
стороны, длина этой дуги равна 2пr, т.е.
пlа/180=2пr, значит Sбок = пlа/180*l/2 =пrl. Итак,
площадь боковой поверхности конуса с
образующей l и радиусом основания r
выражается формулой: S бок= пrl.

43. Сфера и шар

Сферой называется поверхность, состоящая
из всех точек пространства,
расположенных на данном расстоянии от
данной точки (рис.24). Данная точка
называется центром (на рисунке - О), а
данное расстояние – радиусом (на рисунке
- R). Любой отрезок, соединяющий центр
сферы с какой-либо ее точкой, также
называется радиусом сферы.
R
О
Рис.24

44.

Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр
сферы называются также центром, радиусом и диаметром шара. Еще
шар может быть получен вращением полукруга вокруг его диаметра
(рис.25). При этом сфера образуется в результате вращения
полуокружности.
Объем шара радиуса R равен 4/3пR.
3
С
А
Рис.25
В

45.

В отличии от боковых поверхностей цилиндра и конуса сферу нельзя
развернуть так, чтобы получилось плоская фигура. Поэтому для сферы
непригоден способ вычисления площади с помощью развертки. Для
площади S сферы радиуса R получается формула: S=4пR.
2

46. О себе

Привет всем меня зовут Алеся я учусь в 9г классе
города искитима новосибирской области. Мне
нравится делать презентации особенно по
математике

47. Задача.

На трёх ребрах параллелепипеда даны точки А, В и С. Постройте
сечение параллелепипеда плоскостью ,проходящие через эти точки

48. Задача

Докажите
, что
объем призмы равен
произведению
площади основания
на высоту

49. Задача

Сколько
кожи пойдет
на покрышку
футбольного мяча
радиуса 10см (на швы
добавить 8працентов от
площади поверхности
мяча)