Таблицы. Виды таблиц

1.

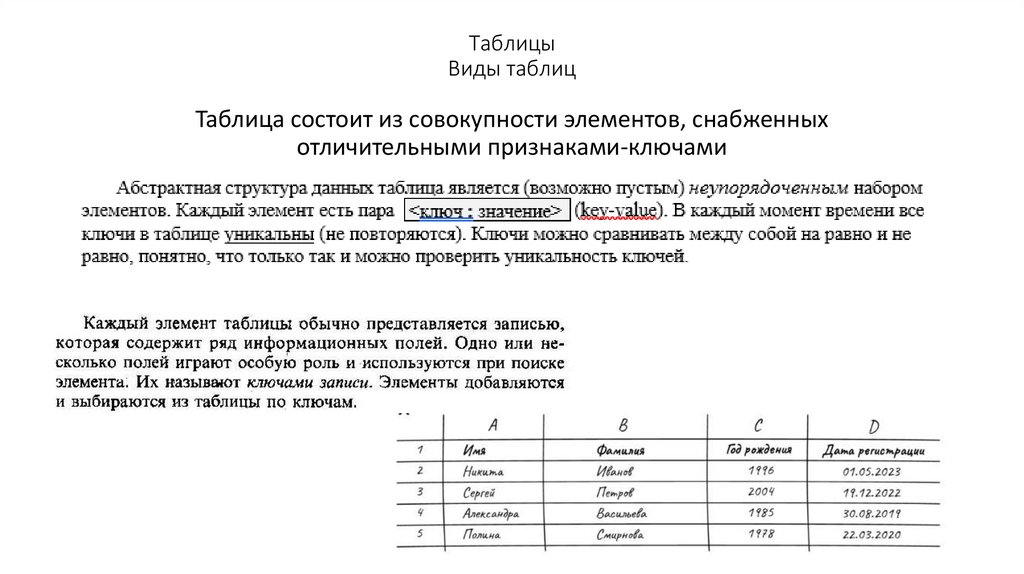
Таблицы
Виды таблиц
Таблица состоит из совокупности элементов, снабженных
отличительными признаками-ключами

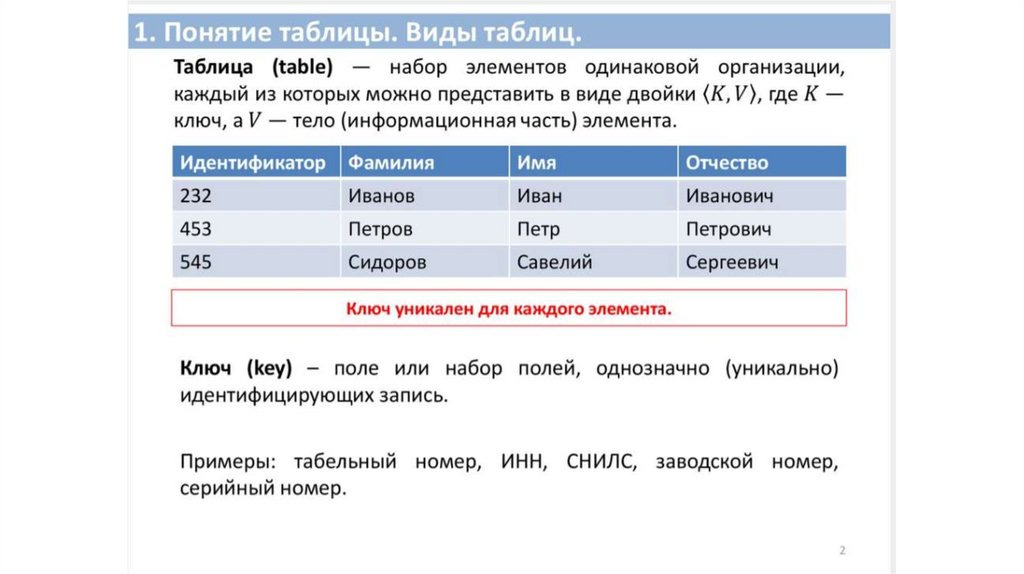
2.

3.

4.

Поиск в таблицах. Условия поиска.
Поиском называется процедура выделения из множества А элементов
подмножества В, содержащего один, несколько или все элементы, признаки
которых удовлетворяют некоторому условию.
Типы условий поиска

5.

6.

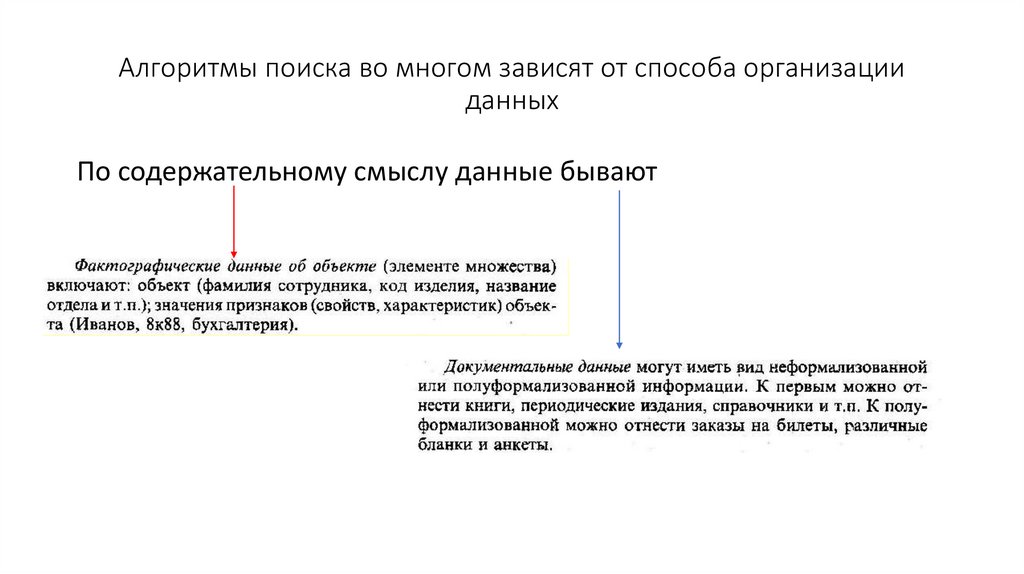
Алгоритмы поиска во многом зависят от способа организации
данных
По содержательному смыслу данные бывают

7.

Линейные таблицы
• Линейная таблица (одномерный массив) — это набор
однотипных данных, которые записываются в одну строку или
один столбец.
• Линейные таблицы в ОП отображаются в массивы или линейные
связанные списки.

8.

Размещение в памяти линейной таблицы
Линейную таблицу можно хранить как в статической, так и в динамической памяти. В памяти таблицу можно
представить как линейным, так и нелинейным связным списком или несвязной структурой.
Мы будем рассматривать таблицы, отображаемые в статической памяти, используя несвязное представление.
Способ 1. Таблица представляется массивом и величиной, задающей фактическое количество элементов таблицы n. N
– максимальное количество элементов в таблице.
struct table
{
type elem[N]; int
n;
} table T;

9.

Размещение в памяти линейной таблицы
Способ 2 . Вместо задания n можно ввести, если это возможно, понятие пустого элемента. Пустой элемент позволяет
определить, пуста таблица, полна таблица или в ней еще есть свободные позиции. Например, если в таблице нет ни
одного пустого элемента, она полна, если первый элемент – пустой элемент, таблица пуста.
type T[N];
Инициализация таблицы: T[0] = "пусто";
Здесь type – тип элемента таблицы, который, как правило,
является сложным типом.

10.

Операции над линейными таблицами

11.

Создание линейной таблицы. Операции над таблицей.
Линейная таблица - это упорядоченный и конечный набор, состоящий из n идентичных элементов. Используется
класс Vector, чтобы представить таблицу, добавить операции вставки, удаления и печати.

12.

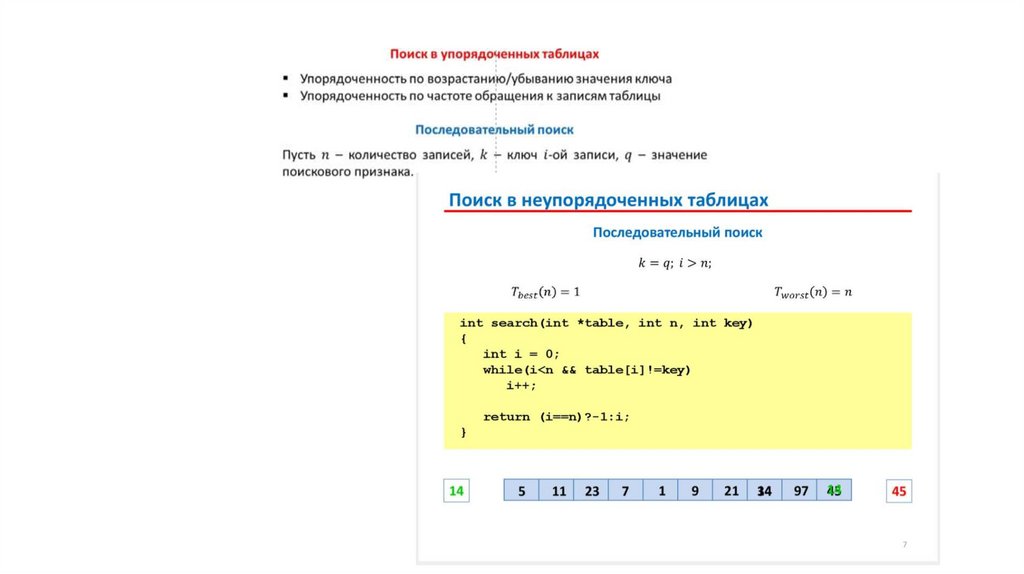
Поиск в неупорядоченных таблицах

13.

14.

Введение заграждающего элемента в процедуру поиска в неупорядоченном
массиве - в последний элемент массива заносится ключ поиска
(заграждающий элемент)

15.

16.

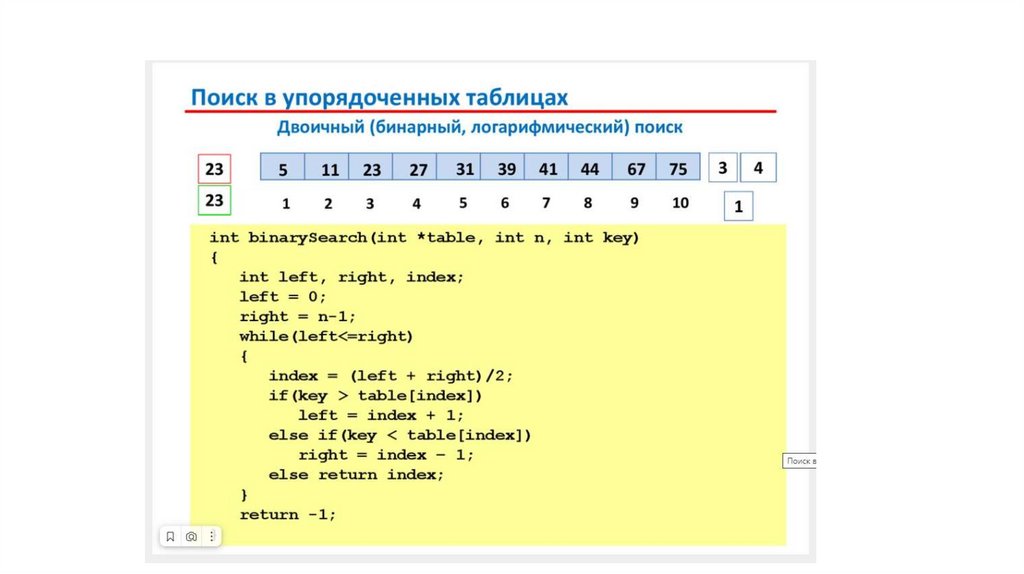
Поиск в упорядоченных таблицах

17.

Алгоритмизация и программирование, язык C++, 10 класс
17
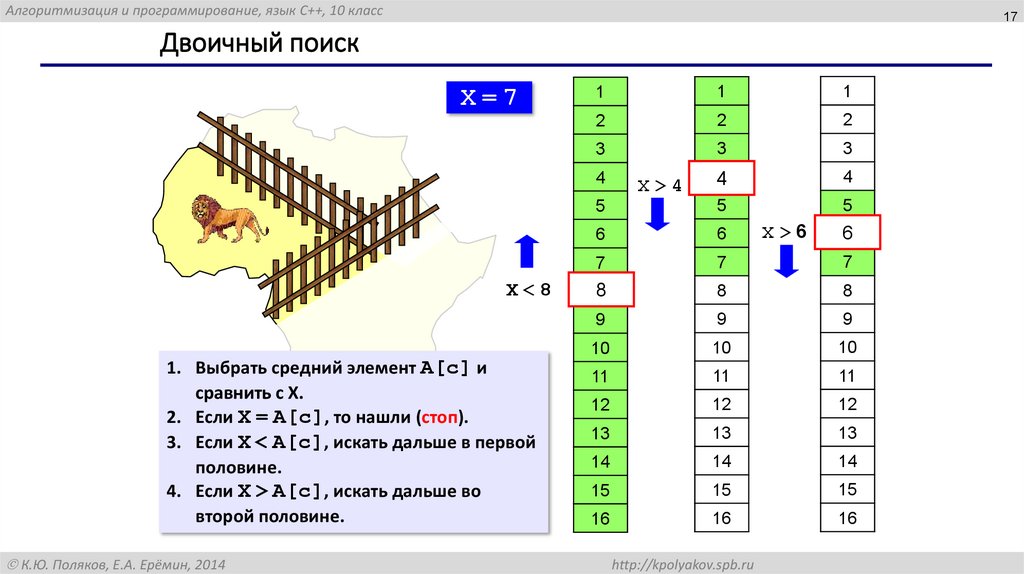
Двоичный поиск
X=7
1
1
1
2
2
2
3
3
3
4
4
5
5
5
6
6
7
7
7
8
8
8
9
9
9
10
10
10
11
11
11
12
12
12
13
13
13
14
14
14
15
15
15
16
16
16
4
X<8
1. Выбрать средний элемент A[c] и
сравнить с X.
2. Если X = A[c], то нашли (стоп).
3. Если X < A[c], искать дальше в первой
половине.
4. Если X > A[c], искать дальше во
второй половине.
К.Ю. Поляков, Е.А. Ерёмин, 2014
X>4
http://kpolyakov.spb.ru
X>6
6

18.

Алгоритмизация и программирование, язык C++, 10 класс
18
Двоичный поиск
X = 44
A[0]
6
34
44
L
67
78
82
с
6
34
L
с
6
34
L
6
55
A[N-1] A[N]
34
L
44
55
R
67
78
82
R
44
55
с
R
44
55
67
78
82
67
78
82
R
! L = R-1 : поиск завершен!
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

19.

Алгоритмизация и программирование, язык C++, 10 класс
19
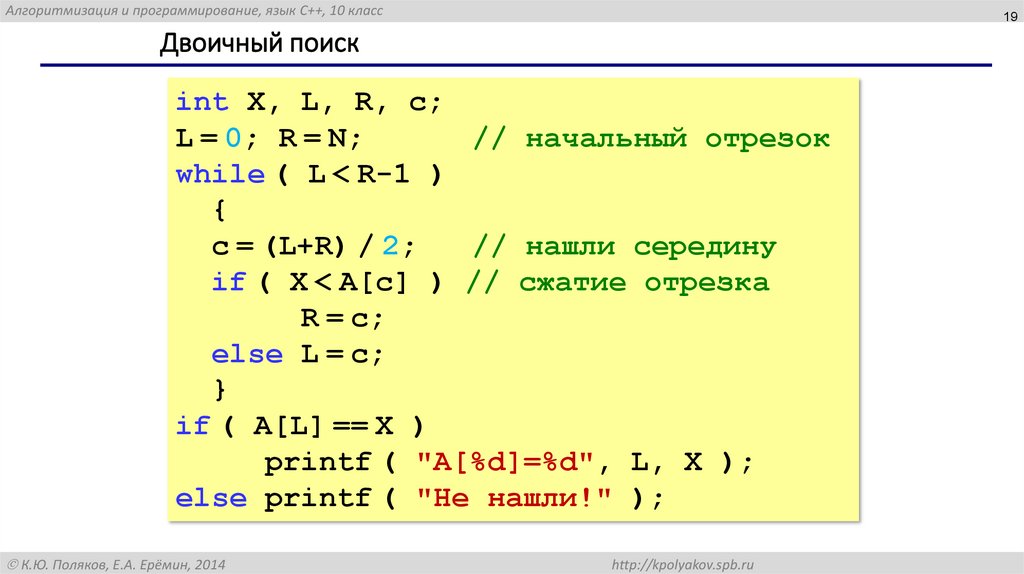
Двоичный поиск
int X, L, R, c;
L = 0; R = N;
// начальный отрезок
while ( L < R-1 )
{
c = (L+R) / 2;
// нашли середину
if ( X < A[c] ) // сжатие отрезка
R = c;
else L = c;
}
if ( A[L] == X )
printf ( "A[%d]=%d", L, X );
else printf ( "Не нашли!" );
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

20.

21.

Алгоритмизация и программирование, язык C++, 10 класс
21
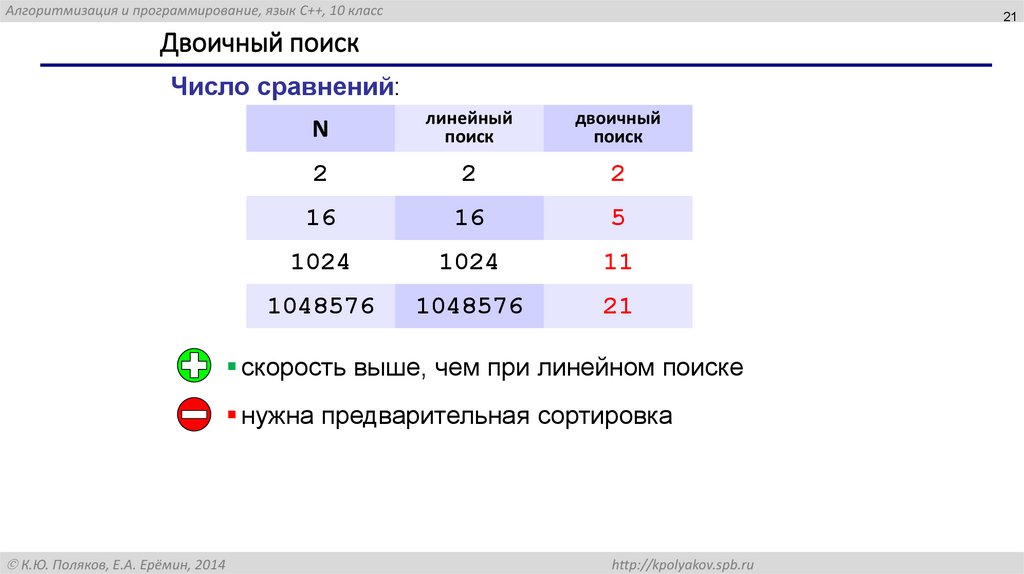
Двоичный поиск
Число сравнений:
N
линейный
поиск
двоичный
поиск
2
2
2
16
16
5
1024
1024
11
1048576
1048576
21
скорость выше, чем при линейном поиске
нужна предварительная сортировка
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

22.

Двоичный поиск

23.

Рекомендации по работе с линейными таблицами

24.

Рекомендации по работе с линейными таблицами

25.

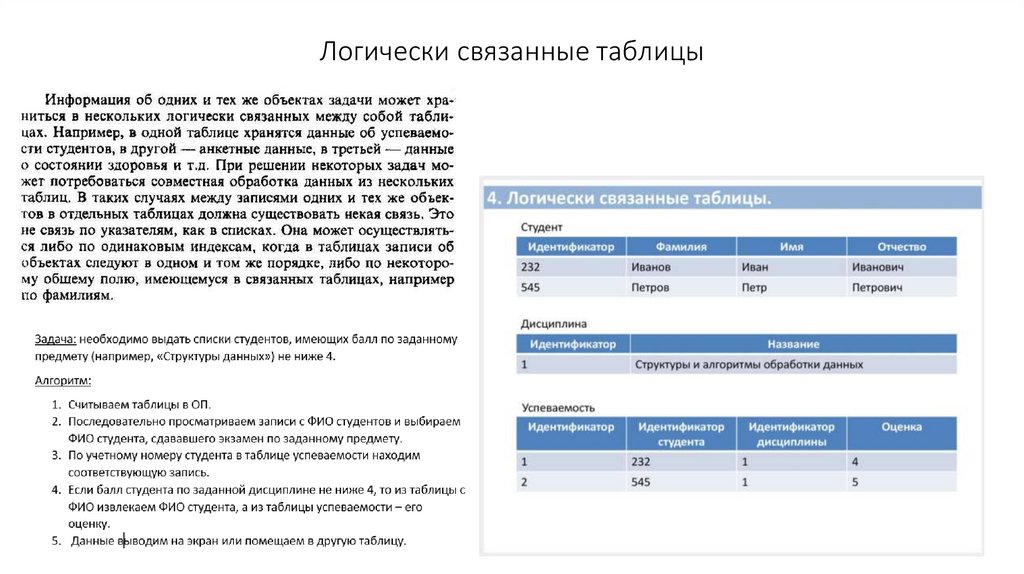
Логически связанные таблицы

26.

Таблицы с вычисляемыми входами
• Скорость доступа к элементам таблицы зависит от двух факторов — способа организации
поиска нужного элемента и размера таблицы. С ростом размера таблицы выбор способа
организации доступа приходится производить прежде всего исходя из критерия скорости
локализации нужного элемента таблицы.
• Элементы таблицы отличаются друг от друга уникальным значением ключевого поля. При
этом ключевыми могут являться не только одно, но и несколько полей элемента таблицы.
Ключ, в том числе и символьный, в памяти представляется последовательностью двоичных
байт. Исходя из того что ключ уникален, соответствующая двоичная последовательность
также будет уникальной.
• Можно использовать уникальное значение ключа для вычисления адреса местоположения
элемента в таблице, это оказывается очень эффективно, так как в идеальном случае доступ к
нужному элементу таблицы осуществляется всего за одно обращение к памяти.
• С другой стороны, на практике часто возникает необходимость размещения элементов
таблицы с достаточно большим диапазоном возможных значений ключевого поля, в то
время, как программа реально использует лишь небольшое подмножество значений этих
ключей. Например, значение ключевого поля может быть в диапазоне 0..3999, но задача
постоянно использует не более 50 значений. В этом случае крайне неэффективным было бы
резервировать память для таблицы размером в 4000 элементов, а реально использовать
чуть больше 1 % отведенной для нее памяти. Гораздо лучше иметь возможность
воспользоваться некоторой процедурой, отображающей задействованное пространство
ключей на таблицу размером, близким к значению 50.

27.

Таблицы с вычисляемыми входами

28.

Таблицы с вычисляемыми входами. Подбор функции расстановки,
обеспечивающий взаимную однозначность преобразования ключа записи в
адрес ее хранения
Таблица с вычисляемым входом представляется в виде массива из N элементов T[i],
i=0,1,…..,N-1, где N-число возможных значений ключей.
Функция расстановки f(k) ставит в соответствие каждому ключу kj некоторое целое i,
различное для разных kj , и такое, что 0<=i<=N-1.

29.

Таблицы с вычисляемыми входами. Подбор функции расстановки,
обеспечивающий взаимную однозначность преобразования ключа записи в
адрес ее хранения

30.

Выбор функции расстановки

31.

Выбор функции расстановки. Функция q(k) должна обеспечивать хорошее
начальное распределение адресов по всей таблице

32.

Выбор функции расстановки. Функция q(k) должна обеспечивать хорошее
начальное распределение адресов по всей таблице

33.

Разрешение коллизий методом цепочек
Методы разрешения коллизий:
• методы цепочек,
• методы открытой адресации.

34.

Методы открытой адресации

35.

Методы открытой адресации
Функции
определяют последовательность адресов для
просмотра элементов таблицы.
Схемы открытой адресации:
-линейная открытая адресация,
-квадратичная открытая адресация,
-открытая адресация с двойным хешированием.

36.

Методы открытой адресации

37.

Особенности алгоритмов удаления записей из таблицы

38.

Особенности алгоритмов удаления записей из таблицы

39.

Переразмещение (рехеширование) таблицы