Функция. График функции

1.

Функция.
График функции.

2.

Машина движется по шоссе с постоянной скоростью
65 км/ч. За время t ч машина проходит путь
S = 65 · t км.
Легко вычислить пройденный путь за любое время:
Если t = 1, то
S = 65 · 1 = 65
Если t = 2, то
S = 65 · 2 = 135
Если t = 3, то
S = 65 · 3 = 195
S = 65 · t
Зависимая переменная
ФУНКЦИЯ
Независимая переменная
АРГУМЕНТ

3.

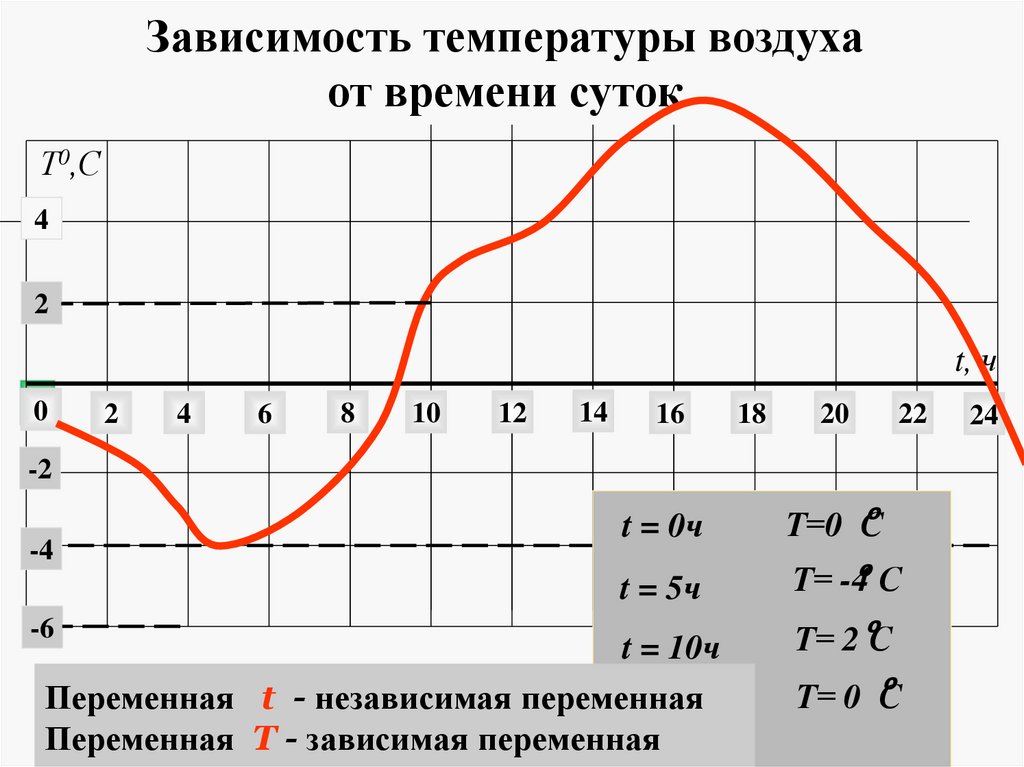
Зависимость температуры воздуха
от времени суток
Т0,С
4
2
t, ч
0
2
4
6
8
10
12
14
16
18
20
22
-2
-4
-6
t = 0ч
Т=0 Со
t = 5ч
Т= -4о С
t = 10ч
Переменная t - независимая переменная
t = 24ч
Переменная T - зависимая переменная
о
Т= 2 С
о
Т= 0 С
24

4.

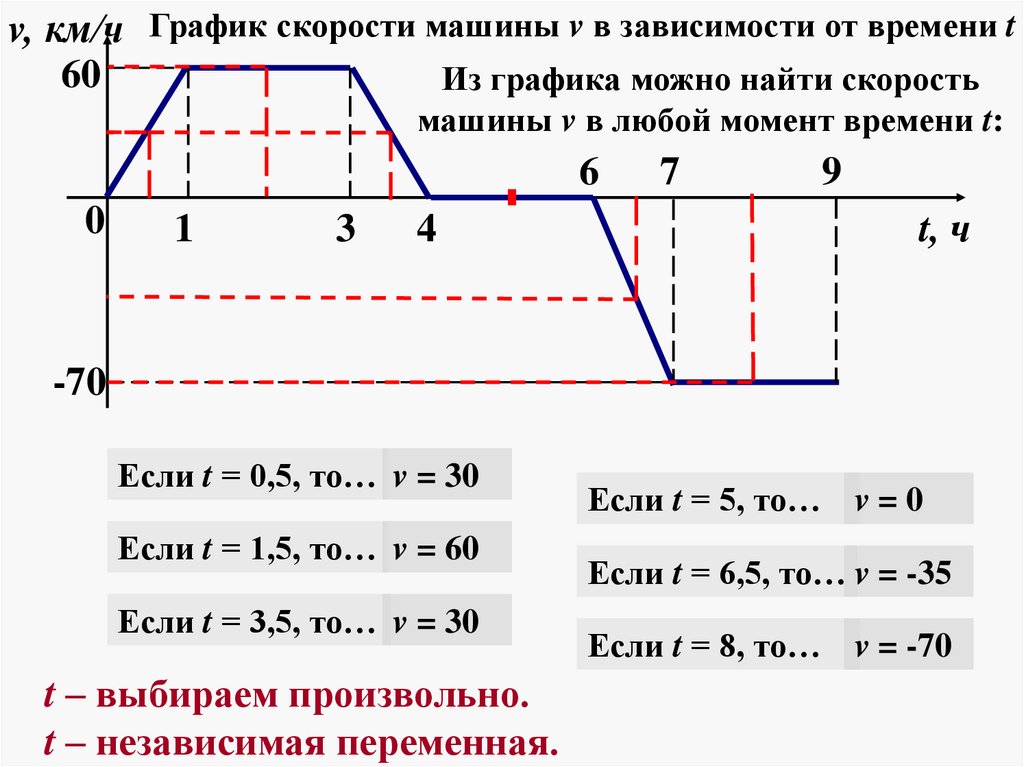
v, км/ч График скорости машины v в зависимости от времени t
60
Описание движения машины
6
0
1
3
7
9
4
t, ч
-70
В течении 1-го часа машина разгоняется до скорости 60 км/ч
От 1ч до 3ч машина движется с постоянной скоростью
От 3ч до 4ч машина тормозит, её скорость уменьшается до 0
От 4ч до 6ч машина стоит, её скорость равна 0
От 6ч до 7ч машина разгоняется до скорости 70 км/ч
От 7ч до 9ч машина движется со скоростью 70 км/ч

5.

v, км/ч График скорости машины v в зависимости от времени t
60
Из графика можно найти скорость
машины v в любой момент времени t:
6
0
1
3
4
7
9
t, ч
-70
Если t = 0,5, то… v = 30
Если t = 1,5, то… v = 60
Если t = 3,5, то… v = 30
t – выбираем произвольно.
t – независимая переменная.
Если t = 5, то… v = 0
Если t = 6,5, то… v = -35
Если t = 8, то… v = -70

6.

Зависимость площади квадрата
от длины его стороны
S = a2
a=2
S=4
a=3
S=9
ФУНКЦИЯ
a=4
S = 16
АРГУМЕНТ

7.

Таблица кубов натуральных чисел:
х
1
2
3
4
5
у = х3
1
8
27
64
125
х
6
7
8
9
10
у = х2 216
343
512
729
1000
Для каждого значения х можно найти
единственное значение у
у = х3
ФУНКЦИЯ
АРГУМЕНТ

8.

В рассмотренных примерах
каждому значению независимой
переменной соответствует
единственное значение
зависимой переменной.
Такую зависимость одной
переменной
от другой называют
функциональной зависимостью
или функцией.

9.

Задание.
На каком рисунке изображён график функции?
Каждому значению
аргумента
у
соответствует единственное
значение функции
у
Молодец!
Подумай!
х
0
1.
х
0
2.

10.

Область значения и
область определения функции.
v, км/ч График скорости машины v в зависимости от времени t
60
6
0
1
3
7
9
t, ч
4
-70
Какие значения (по графику) принимает t ?
0≤t≤9
Какие значения (по графику) принимает v ?
-70 ≤ v ≤ 60
Область определения
Область значения

11.

Область определения и
область значения функции.
Машина движется по шоссе с постоянной скоростью
65 км/ч. За время t ч машина проходит путь
S = 65 · t км.
Какие значения может принимать t ?
t≥0
Какие значения может принимать S ?
S≥0
Все значения, которые принимает
независимая переменная образуют
область определения функции(ООФ)
Значения зависимой переменной
образуют
область значений функции (ОЗФ)

12.

График функции.
График функции – это множество всех точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты – соответствующим
значениям функции.
Вспомним:
II
I
III
IV

13.

График функции.
График функции – это множество всех точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты – соответствующим
значениям функции.
Вспомним:
(-4;
(5;
-3)
(2; 6)
0)

14.

Задание.
По графику функции, изображённому на
рисунке, найти:
1) значение функции при х = 2;4;
2) значение аргумента при котором у = 1;4
1.
х=2
у=1
х=4
у=4
4
2
2.
у = 0,5
х=1
у=2
х=3
0,5
2
3
4

15.

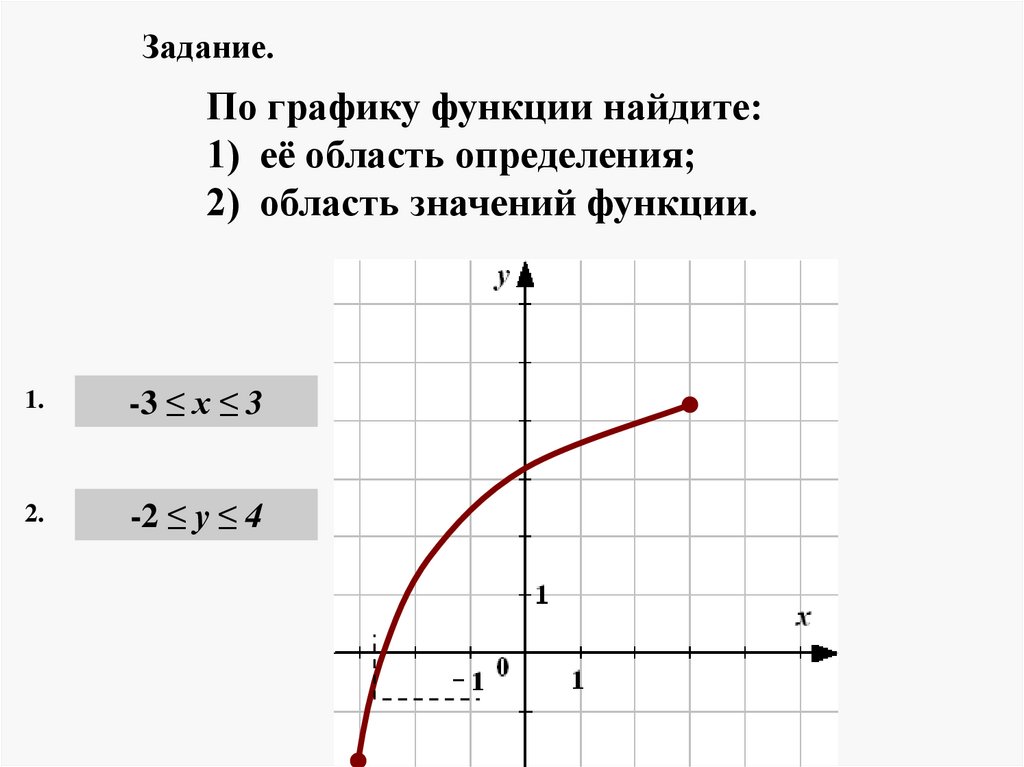
Задание.
По графику функции найдите:
1) её область определения;
2) область значений функции.
y
1.
х – любое число
2.
у ≥ -1
1
0 1
x

16.

Задание.
По графику функции найдите:
1) её область определения;
2) область значений функции.
1.
-3 ≤ х ≤ 3
2.
-2 ≤ у ≤ 4

17.

Задание.
По графику функции найдите:
1) её область определения;
2) область значений функции.
1.
-3 < х < 4
2.
-1 < у < 6

18.

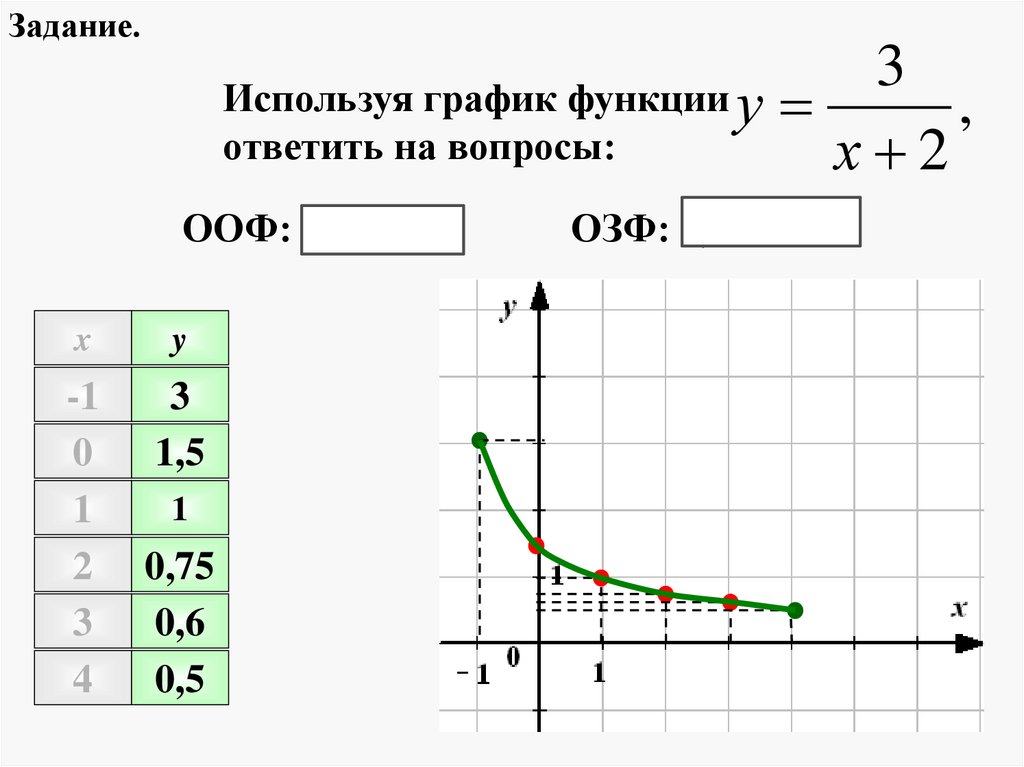
Задание.
3
Используя график функции у
,
ответить на вопросы:
х 2
ООФ: -1 ≤ х ≤ 4
x
y
-1
0
1
2
3
4
3
1,5
1
0,75
0,6
0,5
ОЗФ: 0,5 ≤ х ≤ 3

19.

Пример 2.
Рассмотрим функцию у(х) =
1, если х > 0
0, если х = 0.
-1, если х < 0
Данное выражение задаёт функцию и для любого
значения х легко найти величину у.
1.
у(3,7) = 1 Т.к. х > 0, то пользуемся первой строчкой.
2.
у(0) = 0
3.
у(-2) = -1 Т.к. х < 0, то пользуемся третьей строчкой.
Т.к. х = 0, то используем вторую строчку.

20.

Функция задана формулой
Найти ООФ:
У=
6
х 2 9
Найдём значение аргумента при которых формула
как функция имеет смысл.
Т.к. формула представляет собой дробь, то её
знаменатель не может равняться нулю, т.е.
(х-3)(х+3) 0 , откуда
х 3 и х -3
Итак, область определения данной функции –
Все значения х, кроме чисел -3 и 3

21.

Способы
задания
функция
Формула
Таблица
График

22.

Аналитический
(формулой)
2
f(x)= - х +5

23.

Формула позволяет для любого
значения аргумента находить
соответствующее значение функции
путём вычислений.
Пример 1.
Найти значение функции y(x) = x3 + x
при х = - 2; х = 5; х = а; х = 3а.
1.
у(-2) = (-2)3 + (-2) = -8 – 2 = -10
2.
у(5) = 53 + 5 = 125 + 5 = 130
3.
у(а) = а3 + а

24.

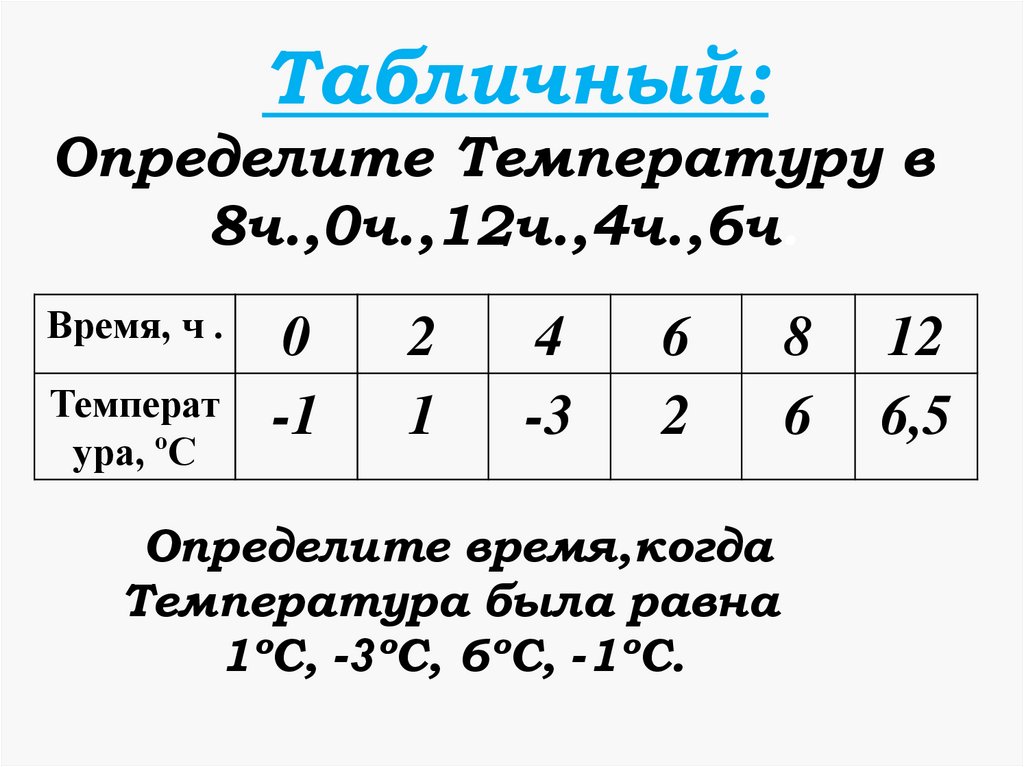
Табличный:
Определите Температуру в
8ч.,0ч.,12ч.,4ч.,6ч.
Время, ч .
Температ
ура, ºС
0
-1
2
1
4
-3
6
2
Определите время,когда
Температура была равна
1ºС, -3ºС, 6ºС, -1ºС.
8
6
12
6,5

25.

Графический:
Найдите:
а)ООФ, ОЗФ
1
0
-1
б) f(0), f(-1,5), f(-5), f(6).

26.

Найдите х
при заданном
значении у:
Укажите
ООФ, ОЗФ
0
у=0, у=-3,
у=1,у=-2,
у=2, у=4.
1
-1

27.

Домашнее задание:
Задание 1:
Построить график функции х2 – 4х, где - 1 ≤ х ≤ 4
Задание 2: Построить график
функции