Similar presentations:
Циклический список
1. Циклический список
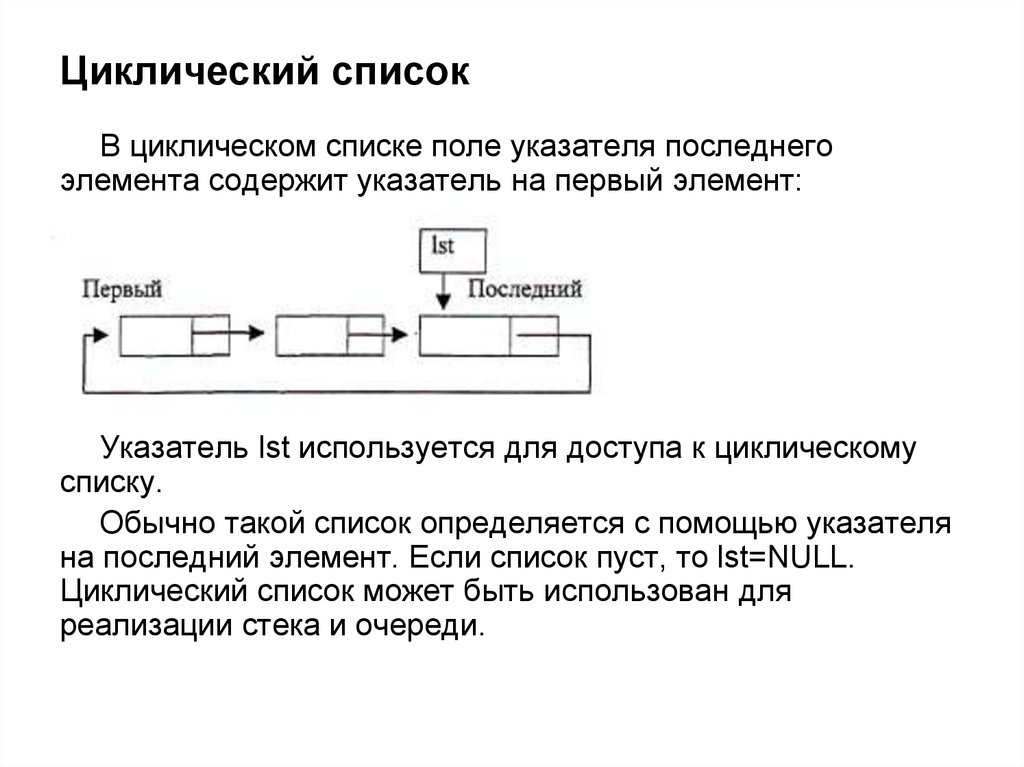
В циклическом списке поле указателя последнегоэлемента содержит указатель на первый элемент:
Указатель lst используется для доступа к циклическому
списку.
Обычно такой список определяется с помощью указателя
на последний элемент. Если список пуст, то lst=NULL.
Циклический список может быть использован для
реализации стека и очереди.
2.
Пустая очередь:lst
p
lst
NULL
Очередь не пуста:
lst
p
p=lst p
lst
Новый элемент добавляется после последнего,
так как это очередь.
Подпрограмма занесения значения X в очередь
на базе циклического списка.
3. Подпрограмма занесения значения X в очередь на базе циклического списка.
node *add_elem(node *lst, int x){
node *p;
p= new node;
p->info=x;
if (lst==NULL) p->next=p; //очередь пуста
else //очередь не пуста
{
p->next=lst->next;
lst->next=p;
}
lst=p; return(lst);
}
4.
void printspisok_1(node *lst) //вывод списка на экран{node *p; p=lst;
do{p=p->next;
cout<<p->info<<“ ”;
}
while(p!=lst);
cout<<endl;
}
void free_memory_1(node *lst) //освобождение памяти
{node *curr, *pred; pred=lst->next;
if (lst==lst->next) delete (lst); //единственный элемент
else
{
do
{curr=pred->next;
delete (pred);
pred=curr;
}
while(pred!=lst);
delete (lst); //последний оставшийся элемент
}
cout<< “\nNow memory is free";}
5.
int main(){node *lst=NULL;
int n=1;
cout<<"Enter positive integers \n";
while(n>0)
{cin>>n;
if(!cin.fail()&&n>0)
lst=add_elem(lst,n);
}
if(lst) //список создан
{ printspisok_1(lst);
free_memory_1(lst);
}
else
cout<<"list is empty";
return 0;
}
6. Двунаправленные связанные списки
Каждый элемент содержит два указателя: на следующий и напредыдущий элемент.
Такие списки могут быть использованы для организации
очереди и стека.
Пример : Занесение X в стек на базе линейного двунаправленного
связанного списка.
#include <iostream>
using namespace std;
struct node2
{
node2 *next, *prev;
int info;
};
7.
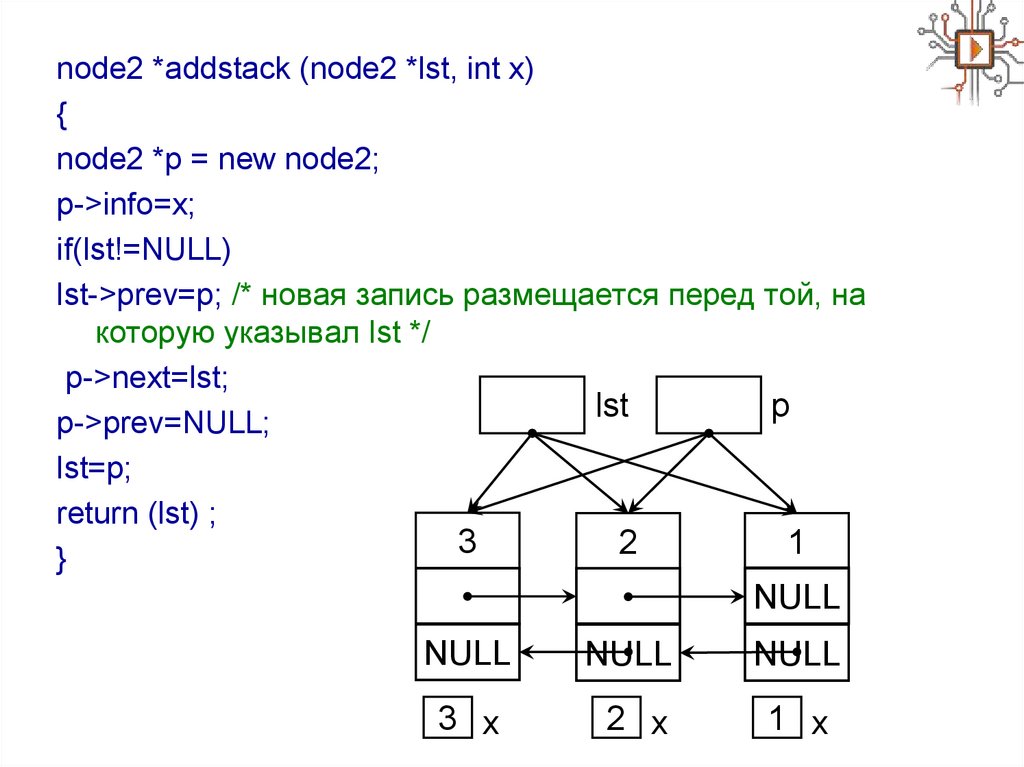
node2 *addstack (node2 *lst, int x){
node2 *p = new node2;
p->info=x;
if(lst!=NULL)
lst->prev=p; /* новая запись размещается перед той, на
которую указывал lst */
p->next=lst;
lst
p
p->prev=NULL;
lst=p;
return (lst) ;
3
2
1
}
NULL
NULL
NULL
NULL
3 x
2 x
1 x
8.
void printlist_2(node2 *lst){ node2 *p,*t;
p=lst;
cout<<"forward";
while(p)
{
cout<<“ “<<p->info;
t=p;p=p->next;
}
cout<<"\nback";
p=t;
while(p)
{
cout<<“ “<<p->info;
p=p->prev;
}
cout<<endl;
}
9.
void free_memory2(node2 *lst) //аналогично односвязному списку{ node2 *now=lst, *next=lst;
while (next)
{next=now->next;
delete(now);
now=next;
}
cout<<"\nNow memory is free";
}
int main()
{ node2 *lst=NULL; int n=1;
cout<<"Enter positive integers \n";
while(n>0)
{cin>>n;
if(!cin.fail()&&n>0)
lst=addstack(lst,n);}
if (lst)
{ printlist_2(lst);
free_memory2(lst); }
else cout<<" No list";
return 0;}
10. Задача. Написать функцию для удаления элементов меньших чем X1 из циклического однонаправленного списка. Используем указатели:
lst – указатель на последний элемент, pred –предшествующий, next – следующий, t – новый последний
элемент списка. Рассмотрим случаи:
• удаление первого и единственного
lst
lst NULL
• удаление первого и не единственного
pred=lst=t
tek
lst
pred
• удаление элемента из середины списка
pred
tek
tek
lst
11.
node * del (node *lst, int x1){
node *tek,*pred, *t;
tek=lst->next; //указатель на текущий элемент
pred=lst; //указатель на предыдущий элемент
while (lst&&lst->info<x1) //пока удаляется первый элемент
if (lst->next==lst) //если элемент первый и единственный
{
delete(lst); lst=NULL;
}
else //если первый и не единственный
{ t=lst; //поиск нового lst – он будет перед исходным lst
do
t=t->next;
while (t->next!=lst);
t->next=pred->next;
delete(lst);
lst=t;
pred=t;
}
12.
if (lst!=NULL)//если список еще не удален полностью
do
if (tek->info<x1)
{ //удаление элемента из середины списка
pred->next=tek->next;
delete(tek);
tek=pred->next;
}
else //движение по списку
pred=tek,tek=tek->next;
while (tek!=lst);
return(lst);
}
13. Бинарные деревья
Бинарное дерево - конечное множество элементов,которое либо пусто, либо содержит один элемент,
называемый корнем дерева. Остальные элементы
множества делятся на два непересекающихся
подмножества, каждое из которых является бинарным
деревом. Эти подмножества называются левым и
правым поддеревьями исходного дерева. Каждый
элемент бинарного дерева называется узлом.
Если X - корень бинарного дерева и Y - корень его
левого или правого поддерева, то говорят,
что X - отец Y, Y - левый или правый сын X.
Узлы, не имеющие сыновей, называются листьями.
Два узла называются братьями, если они сыновья
одного отца.
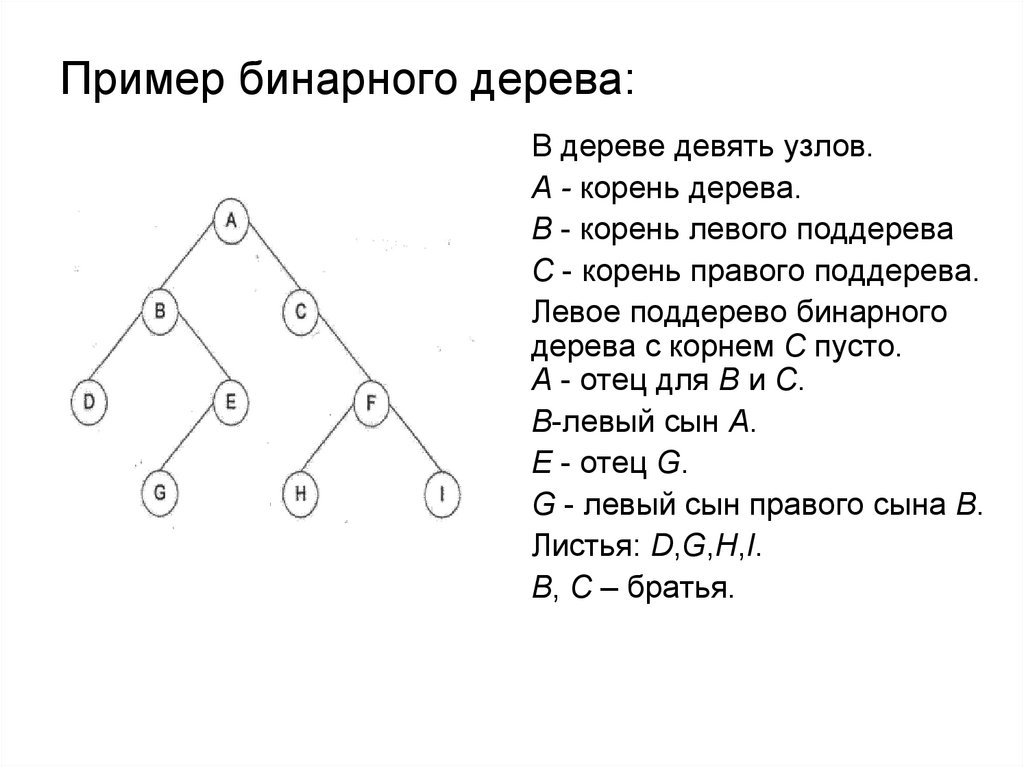
14. Пример бинарного дерева:
В дереве девять узлов.А - корень дерева.
В - корень левого поддерева
С - корень правого поддерева.
Левое поддерево бинарного
дерева с корнем С пусто.
А - отец для В и С.
В-левый сын А.
E - отец G.
G - левый сын правого сына В.
Листья: D,G,H,I.
В, С – братья.
15. Прохождение бинарного дерева
Обычно дерево сначала строится, азатем обходится. Как отметить каждый
узел один раз? В линейном списке
элементы просматриваются от начала до
конца. Для узлов дерева не существует
такого естественного порядка.
Рассмотрим три метода прохождения,
которые определяются рекурсивно.
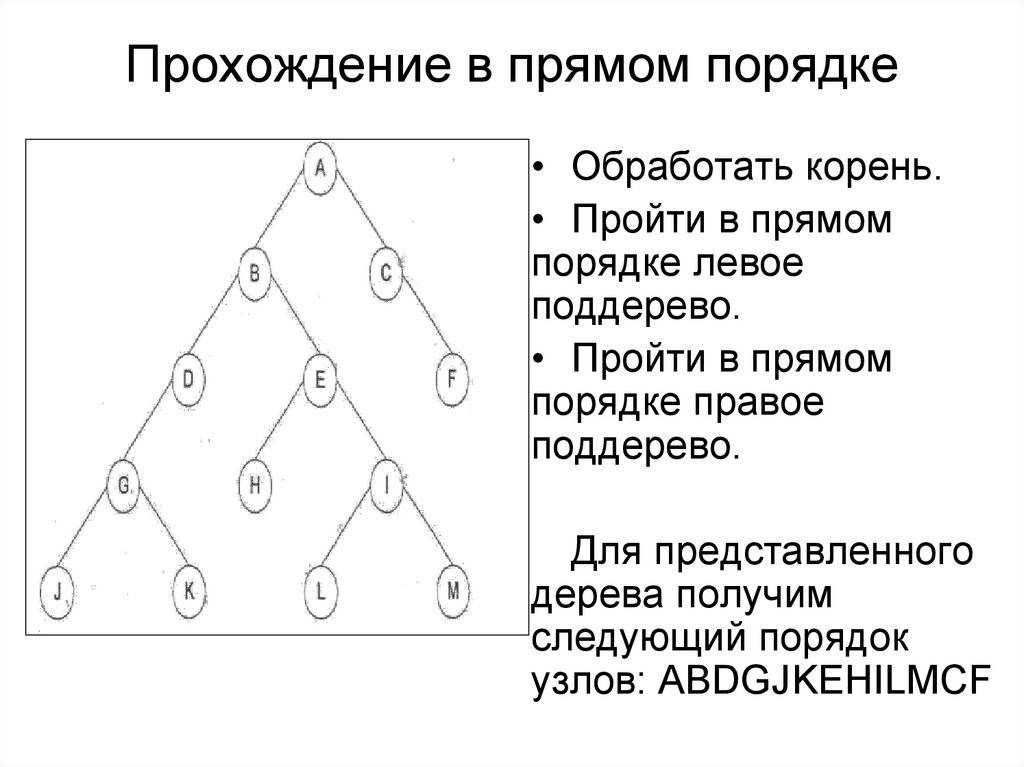
16. Прохождение в прямом порядке
• Обработать корень.• Пройти в прямом
порядке левое
поддерево.
• Пройти в прямом
порядке правое
поддерево.
Для представленного
дерева получим
следующий порядок
узлов: ABDGJKEHILMCF
17. Прохождение в обратном порядке
• Пройти в обратномпорядке левое
поддерево.
• Пройти в обратном
порядке правое
поддерево.
• Обработать корень.
Получим:
JKGDHLMIEBFCA
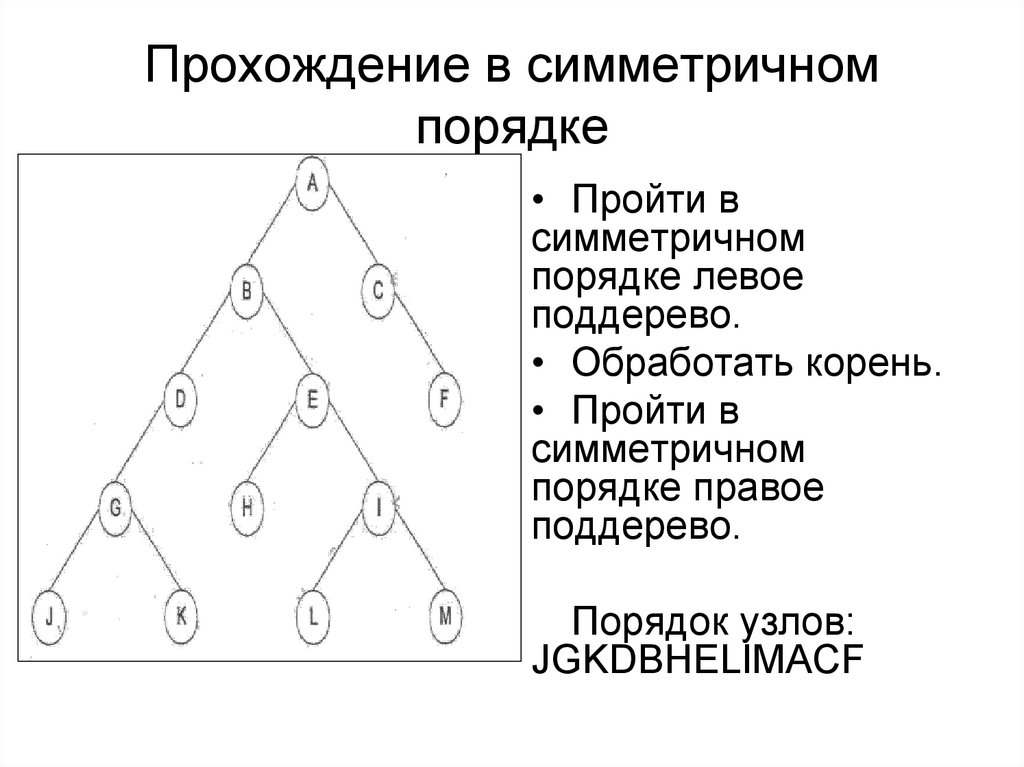
18. Прохождение в симметричном порядке
• Пройти всимметричном
порядке левое
поддерево.
• Обработать корень.
• Пройти в
симметричном
порядке правое
поддерево.
Порядок узлов:
JGKDBHELIMACF













 programming
programming