История вычислительной техники

1. ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

2.

1. Домеханический этап
Древние средства счета
Кости с зарубками
(«вестоницкая кость», Чехия,
30 тыс. лет до н.э)
Узелковое письмо (Южная
Америка, VII век н.э.)
узлы с вплетенными камнями
нити разного цвета (красная –
число воинов, желтая – золото)
десятичная система

3.

Саламинская доска
о. Саламин в Эгейском море (300 лет до н.э.)
• бороздки – единицы, десятки, сотни, …
• количество камней – цифры
• десятичная система

4.

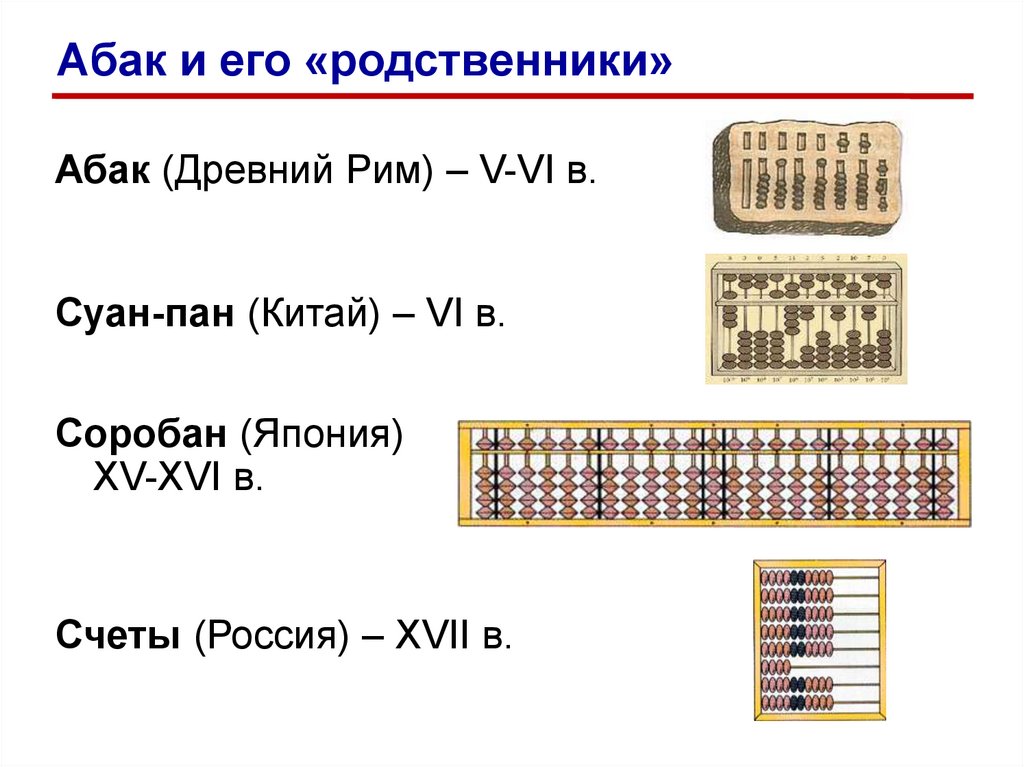
Абак и его «родственники»
Абак (Древний Рим) – V-VI в.
Суан-пан (Китай) – VI в.
Соробан (Япония)
XV-XVI в.
Счеты (Россия) – XVII в.

5. Ручной этап.

Греческий абак
Впервые абак появился,
вероятно, в Древнем Вавилоне
3 тыс. до н. э. Первоначально
представлял собой доску,
разграфлённую на полосы или со
сделанными углублениями.
Счётные метки (камешки или
косточки) передвигались по
линиям или углублениям. В 5 в.
до н. э. в Египте вместо линий и
углублений стали использовать
палочки и проволоку с
нанизанными камешками.

6. Суан-пан.

Суан-пан (5 век до нашей эры). У китайцев в основе счета
лежала не десятка, а пятерка, рамка китайских счетов суанпан имеет более сложную форму. Она разделена на две
части: в верхней части на каждом ряду располагаются по 5
косточек, в нижней части - по две. Таким образом, для того
чтобы выставить на этих счетах число 6, ставили
сначала косточку, соответствующую пятерке, и затем
прибавляли одну в разряд единиц.
Серобян
В V-IV в. до н.э. в Азии Китай интенсивно развивает
торговлю с Японией, Индией и Кореей. Торговцам был
необходим способ для подсчета заказов и выручки. Так
или иначе, из этой потребности, были рождены счеты. В
Китае они назывались "суан-пан", в Западной Европе и у
греков - "абак" (abacus), у японцев - "серобян".

7. Русские Счёты.

Счеты - первый истинный предшественник счетных
машин и компьютеров. Вычисления на них проводились
с помощью перемещения счетных костей и камешков
(калькулей) в углублениях досок из бронзы, камня,
слоновой кости. Эти счеты сохранились до эпохи
возрождения, а в видоизмененном виде, сначала как
"дощатый щот" и как русские счеты - до наших дней.
Вычисления на них выполнялись следующим образом:
Значение, назначенное для каждой косточки,
определяется не ее формой, а позицией, в которой она
расположена. Одна косточки имеет значение 1; Две
вместе имеют значение 2. Косточка на следующей
линии, имеет уже значение 10, а косточка на третьей
линии имеет значение 100. Следовательно, три
правильно расположенных косточки - две со значениями
1 и одна со значением 10 - будут означать 12, а
добавление четвертой косточки со значением 100 будет
уже означать 112. Использование таких значений,
связанных с местом косточек, это сокращенная форма
системы вычислений с основанием 10.

8.

Логарифмитическая линейка
Открытие логарифмов и логарифмических таблиц Дж.
Непером в начале XVII в., позволивших заменять умножение и
деление соответственно сложением и вычитанием, явилось
следующим крупным шагом в развитии вычислительных
систем ручного этапа. Логарифмы послужили основой
создания замечательного вычислительного инструмента логарифмической линейки, более 360 лет служащего
инженерно-техническим работникам всего мира.
Логарифмическая линейка может выполнять несколько
математических операций, в том числе умножение и деление
чисел, возведение в степень (чаще всего в квадрат и куб) и
вычисление квадратных и кубических корней, вычисление
логарифмов, тригонометрических функций и другие операции

9.

2. Механический этап
Первые проекты счетных машин
Леонардо да Винчи (XV в.) –
суммирующее устройство с
зубчатыми колесами:
сложение 13-разрядных чисел
Вильгельм Шиккард (XVI в.) –
суммирующие «счетные часы»:
сложение и умножение
6-разрядных чисел
(машина построена,
но сгорела)

10.

’
«Паскалина»
(1642)
Блез Паскаль (1623 - 1662)
• машина построена!
• зубчатые колеса
• сложение и вычитание
8-разрядных чисел
• десятичная система

11. Паскалина

Машина Паскаля представляла собой механическое
устройство в виде ящичка с многочисленными
связанными одна с другой шестерёнками.
Складываемые числа вводились в машину при
помощи соответствующего поворота наборных
колёсиков. На каждое из этих колёсиков,
соответствовавших одному десятичному разряду
числа, были нанесены деления от 0 до 9. При вводе
числа, колесики прокручивались до
соответствующей цифры. Совершив полный оборот,
избыток над цифрой 9 колёсико переносило на
соседний разряд, сдвигая соседнее колесо на 1
Первые варианты «Паскалины» имели пять зубчатых колёс,
позицию.
позднее их число увеличилось до шести или даже восьми,
что позволяло работать с большими числами, вплоть до
9999999. Ответ появлялся в верхней части металлического
корпуса. Вращение колёс было возможно лишь в одном
направлении, исключая возможность непосредственного
оперирования отрицательными числами. Тем не менее,
машина Паскаля позволяла выполнять не только сложение,
но и другие операции, но требовала при этом применения
довольно неудобной процедуры повторных сложений.
Вычитание выполнялось при помощи дополнений до девятки,
которые для помощи считавшему появлялись в окошке,
размещённом над выставленным оригинальным значением.

12.

Машина Лейбница (1672)
Вильгельм Готфрид Лейбниц
(1646 - 1716)
• сложение, вычитание, умножение,
Арифмометр «Феликс»
деление!
(СССР, 1929-1978) –
• 12-разрядные числа развитие идей машины
• десятичная система Лейбница

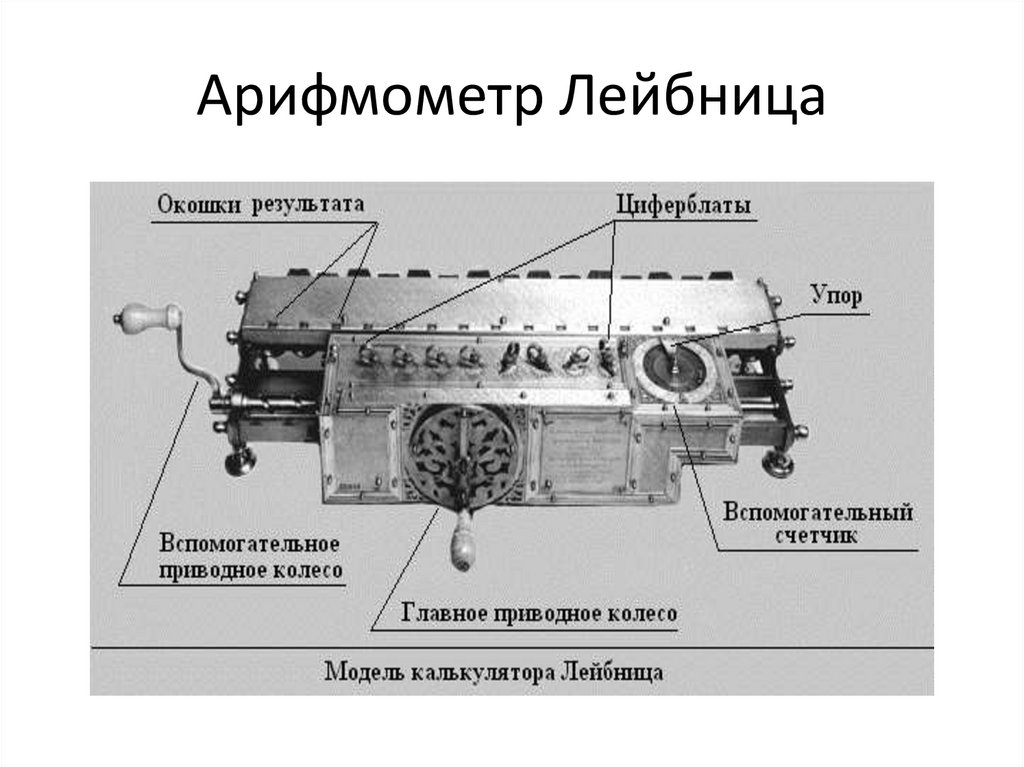
13. Арифмометр Лейбница

14. Умножение и деление: Арифмометры предназначены, в первую очередь, для умножения и деления. Поэтому почти у всех арифмометров

есть устройство,
отображающее количество
сложений и вычитаний —
счётчик оборотов
Сложение и вычитание:
Арифмометры могут выполнять
сложение и вычитание. Но на
примитивных рычажных моделях
эти операции выполняются очень
медленно — быстрее, чем
умножение и деление, но заметно
медленнее, чем на простейших
суммирующих машинах или даже
вручную

15.

Машина Лейбница (1672)
Арифмометр «Феликс»
(СССР, 1929-1978) – развитие идей
машины Лейбница

16.

Машины Чарльза Бэббиджа
Разностная машина (1822)
Аналитическая машина (1834)
• «мельница» (автоматическое
выполнение вычислений)
• «склад» (хранение данных)
• «контора» (управление)
• ввод данных и программы с
перфокарт
• ввод программы «на ходу»
Ада Лавлейс
(1815-1852)
первая программа – вычисление
чисел Бернулли (циклы, условные переходы)
1979 – язык программирования Ада

17. Машина Беббиджа.

Для хранения чисел Бэббидж
предложил использовать набор
десятичных счетных колес. Каждое из
колес могло останавливаться в одном
из десяти положений и таким
образом запоминать один
десятичный знак. Колеса собирались
в регистры для хранения
многоразрядных десятичных чисел.
По замыслу автора запоминающее
устройство должно было иметь
емкость в 1000 чисел по 50
десятичных знаков "для того, чтобы
иметь некоторый запас по отношению
к наибольшему числу, которое может
потребоваться".

18.

1936 г. - двадцатипятилетний студент Кембриджского
университета англичанин Алан Тьюринг опубликовал
статью “О вычисляемых числах”, в которой
рассматривалось гипотетическое устройство (машина
Тьюринга), пригодное для решения любой
разрешимой математической или логической задачи, прообраз программируемого компьютера.
Пост (Post) Эмиль Леон американский математик и
логик. Читал лекции по математике и логике в
Колумбийском, Нью-Иоркском и др. университетах США.
В 1936 г Эмиль Пост предложил абстрактную
вычислительную машину - машину Поста. Она
отличается от машины Тьюринга большей простотой.
Обе машины "эквивалентны" и были созданы для
уточнения понятия "алгоритм

19. Машина Тьюринга

Машина Тьюринга имеет бесконечную в обе
стороны ленту, разделенную на квадратики
(ячейки). В каждой ячейке может быть
записан некоторый символ из
фиксированного (для данной машины)
конечного множества, называемого
алфавитом данной машины. Один из
символов алфавита выделен и называется
"пробелом", предполагается, что изначально
вся лента пуста, то есть заполнена
пробелами.
Машина Тьюринга может менять
содержимое ленты с помощью
специальной читающей и пишущей
головки, которая движется вдоль ленты.
В каждый момент головка находится в
одной из ячеек. Машина Тьюринга
получает от головки информацию о том,
какой символ та видит, и в зависимости
от этого решает, что делать, то есть
какой символ записать в текущей ячейке
и куда сдвинуться после этого. При этом
также меняется внутреннее состояние
машины. Еще надо договориться, с чего
начинается и когда кончается работа.

20. Машина Поста

Машина Поста состоит из каретки (или
считывающей и записывающей головки) и
разбитой на секции ленты, считающейся
условно бесконечной в обе стороны. В каждой
клетке может быть записан символ из
фиксированного алфавита. В любой конкретный
момент головка обозревает одну клетку и
способна работать только с ней.
Работа машины Поста определяется
программой с конечным числом строк.
Программа состоит из команд, имеющих
по 3 поля, в которых записываются: №
команды, операция и отсылка.

21. Машина Холлерита

Первый счетно-аналитический комплекс был
создан в США Г. Холлеритом в 1887 г. и состоял
из ручного перфоратора, сортировочной
машины и табулятора. Значение работ Г.
Холлерита для развития ВТ определяется
двумя основными факторами. Во-первых, он
стал основоположником нового направления в
ВТ — счетно-перфорационного (счетноаналитического), состоящего в применении
табуляторов и сопутствующего им
оборудования для выполнения широкого круга
экономических и научно-технических расчетов.
На основе этой ВТ создаются
машинно-счетные станции для
механизированной обработки
информации, послужившие
прообразом современных
вычислительных центров (ВЦ). В
20—30-е годы 20 века применение
счетно-перфорационной техники
становится ведущим фактором
развития ВТ; только появление ЭВМ
ограничило ее применение.

22.

Прогресс в науке
• Основы математической логики:
Джордж Буль (1815 - 1864).
• Электронно-лучевая трубка
(Дж. Томсон, 1897)
• Вакуумные лампы – диод, триод (1906)
• Триггер – устройство для
хранения бита (М.А. Бонч-Бруевич,
1918).
• Использование математической логики
в компьютерах (К. Шеннон, 1936)

23.

3. Электромеханический этап
Электромеханический этап развития ВТ явился наименее продолжительным и
охватывает всего около 60 лет — от первого табулятора Германа Холлерита (1887
г.) до первой ЭВМ ЕNIАС (1945 г.).
В 1890 году американец Герман
Холлерит создал машину для
проведения переписи населения в
США. Перфокарты выступали в ней в
качестве носителя информации, (то
есть внешнего запоминающего
устройства). Впервые для расчетов
было использовано электричество. Он
создал фирму - прообраз IBM. . Вскоре
в 1924 году Холлерит основал фирму
IBM для серийного выпуска
табуляторов.

24.

Первые компьютеры
1937-1941. Конрад Цузе: Z1, Z2, Z3, Z4.
• электромеханические реле
(устройства с двумя состояниями)
• двоичная система
• использование булевой алгебры
• ввод данных с киноленты
1939-1942. Первый макет электронного
лампового компьютера, Дж. Атанасофф
• двоичная система
• решение систем 29 линейных уравнений

25.

Марк-I (1944)
Разработчик – Говард Айкен (1900-1973)
Первый компьютер в США:
– длина 17 м, вес 5 тонн
– 75 000 электронных ламп
– 3000 механических реле
– сложение – 3 секунды, деление – 12 секунд

26.

Марк-I (1944)
Хранение данных на
бумажной ленте
А это – программа…

27.

Принципы фон Неймана
(«Предварительный доклад о машине EDVAC», 1945)
• Принцип двоичного кодирования: вся
информация кодируется в двоичном
виде.
• Принцип программного управления:
программа состоит из набора команд,
которые выполняются процессором
автоматически друг за другом в
определенной последовательности.
• Принцип однородности памяти:
программы и данные хранятся в одной и той же
памяти.
• Принцип адресности: память состоит из
пронумерованных ячеек; процессору в
любой момент времени доступна любая
ячейка.