Algorytmy zachłanne - idea
1. Algorytmy zachłanne - idea
dzieli problem na podproblemy (etapy)na każdym etapie stara się podejmować
najbardziej korzystny wybór spośród
możliwych wariantów
innymi słowy dokonywany jest szereg
optymalnych lokalnych wyborów z
nadzieja, że przyczynią się one do
uzyskania optymalnego globalnego
rozwiązania
2. Ogólne uwagi o strategii zachłannej
algorytmy są typu optymalizacyjnego(optymalizują wybór na każdym kroku),
aby uzyskać optymalne rozwiązanie całego
problemu
algorytmy zachłanne podejmują szereg
decyzji (bo na każdym kroku dokonują
wyboru spośród dostępnych możliwości)
3. Ogólne uwagi o strategii zachłannej
okazuje się, że działanie na zasadzieszeregu wyborów optymalnych nie zawsze
daje rozwiązanie optymalne (wtedy, gdy
okaże się, że ten wybór bynajmniej
optymalnym nie był) – dla wielu
problemów strategia zachłanna jest jednak
wystarczająca
4. Skąd wiadomo, że rozwiązanie problemu jest optymalne ?
nie ma ogólnej metodywiększość problemów, które daje się
rozwiązać strategią zachłanną cechują dwie
własności: istnienie wyboru zachłannego
(lokalnego wyboru optymalnego
potencjalnie prowadzącego do optymalnego
rozwiązania całego problemu) oraz
optymalnej podstruktury
5. Wybór zachłanny
decyzje podejmowane na każdym kroku sąw tym sensie lokalne, że ustalane kryterium
optymalnego wyboru nie zależy od
rozwiązań poprzednich etapów choć mogą
zależeć od podjętych wcześniej nigdy nie
później decyzji (inaczej niż będzie to miało
miejsce w programowaniu dynamicznym)
po dokonaniu wyboru rozwiązujemy
podproblem z niego wynikający
6. Wybór zachłanny
podejmując kolejno decyzje zachłanneredukujemy problem do coraz mniejszych
podproblemów (metoda zstępująca)
to że wybór zachłanny w każdym kroku
prowadzi do rozwiązania optymalnego
wymaga jeszcze dowodu
zysk z własności wyboru zachłannego to
możliwość efektywnego dokonywania
wyborów w rozważanych podproblemach
7. Optymalna podstruktura
własność polegająca na tym, że optymalnerozwiązanie problemu jest funkcją
optymalnych rozwiązań podproblemów
własność ta jest zasadnicza także dla
stosowalności metod programowania
dynamicznego
8. Problem kasjera (wydawania reszty)
kasjer ma wydać kwotę reszty r przy użyciudostępnych nominałów, z których każdy
występuje w niegraniczonej liczbie w taki
sposób aby użyć jak najmniej monet
9. Strategia zachłanna dla problemu kasjera
wydawanie rozpocząć od nominału onajwyższej wartości biorąc tyle monet ile to
możliwe i redukując w ten sposób problem
do mniejszego (wydanie reszty o mniejszej
wartości)
następnie o ile to możliwe przechodzimy do
nominału o kolejnej niższej wartości i przy
jego pomocy wydajemy największą
możliwą część pozostałe reszty itd., aż do
ew. rozwiązania problemu
10. Wybór zachłanny w problemie kasjera
na każdym etapie resztę próbujemy wydaćjak największym nominałem, aby możliwie
jak najszybciej ograniczyć jej wielkość
11. Czy rozwiązanie globalne jest zawsze optymalne ?
dla dowolnego r przy podanych założeniachgeneralnie tak , ale są przypadki
szczególne..
przypadek realistyczny – nie mamy
nieograniczonej liczby nominałów, każdy
występuje w pewnej liczbie (ale to wbrew
założeniom metody)
specyficzny układ nominałów –okazuje, się,
że rozwiązanie nie tylko nie jest optymalne,
ale wręcz niekiedy nie jest odnalezione !
12. Problem kasjera –przykład dający rozwiązanie
1.r=22, {1,2,10}. Nominały 10 (2 razy) i 2
wydają resztę optymalnie, przy założeniu,
że mamy do dyspozycji tylko te dwa
nominały
13. Przypadek bardzo ciekawy…
r=18. Do dyspozycji wszystkie nominały wnieograniczonej liczbie poza nominałem 1
(przypuśćmy, że dany system monetarny nie
uwzględnia takiego nominału). Strategia
zachłanna nakazuje następujące wybory:
10,5,2 i w tym momencie wobec braku
nominału 1 algorytm wskaże na brak
rozwiązania.
Okazuje się jednak, że ono istnieje nawet przy
braku nominału 1!
18=10+4*2
14. Problem pakowania plecaka
wersja dyskretna, wariant decyzyjnyDany jest plecak o masie (wadze) m oraz n
różnych przedmiotów, z których każdy
występuje w liczbie 1, każdy ma swoja wagę
wi(i=1,..n) oraz cenę (wartość) ci(i=1,…n).
Plecak należy wypełnić dowolnie wybranymi
k z n rzeczy, w taki sposób, aby suma ich wag
nie przekroczyła m, zaś suma ich wartości
była największa z możliwych.
15. Decyzyjny, dyskretny problem plecakowy
istnieje problem z wyborem zachłannym – comiałoby nim być ?
przykłady możliwych wyborów:
- przy wyborze każdej z kolejnych rzeczy
obowiązuje kryterium najmniejszej wagi
- przy wyborze każdej z kolejnych rzeczy
obowiązuje kryterium największej
ceny
- przy wyborze każdej z kolejnych rzeczy
obowiązuje kryterium maksymalizacji ilorazu
cena/waga
16. Kontrprzykład
Rozważmy plecak o masie m=12Niech n=6, a parametry rzeczy są
następujące( w nawiasie najpierw masa, a
potem cena rzeczy):
1- (10,40), 2- (4,30), 3- (3,24), 4- (2,20)
5-(5,35), 6-(8,52)
Wg kryterium najmniejszej wagi i także
największego ilorazu spakowane zostaną te
same rzeczy 2,3 oraz 4- ich wartość 74.
Kryterium największej ceny prowadzi do
spakowania rzeczy 6 i 2 o wartości 82.
17. Kontrprzykład
Tymczasem:Optymalnie spakowany plecak o wartości 89
tworzą rzeczy 2,3 i 5. Tego wariantu nie są w
stanie zaproponować algorytmy oparte o
którekolwiek z zaproponowanych kryteriów
!!!
Dla dyskretnego problemu decyzyjnego nie
ma zatem wyboru zachłannego.
18. ..a własność optymalnej podstruktury ?
ta akurat ma miejsce dla strategii zachłannejrozwiązywania problemu dyskretnego,
decyzyjnego problemu plecakowego
jeśli bowiem przyjąć, że udało się uzyskać
optymalną wartość W przy n rzeczach, to
będzie oznaczało, że po usunięciu z plecaka
rzeczy numer j uzyskamy optymalnie
optymalnie spakowany plecak o wartości
W-wj tworzony przez n-1 rzeczy
19. Inne problemy związane z pakowaniem plecaka
ogólny, dyskretny problem plecakowyciągły problem plecakowy
20. Ogólny, dyskretny problem plecakowy
w stosunku do dyskretnego problemudecyzyjnego zmienia się tylko jedno
założenie : każda rzecz może występować
w liczbie większej niż 1, praktycznie w
dowolnej liczbie
czy to założenie zmienia coś w kwestii
istnienia wyboru zachłannego ?
21. Kontrprzykład
Rozważmy plecak o masie m=23Niech n=6, a parametry rzeczy są
następujące( w nawiasie najpierw masa, a
potem cena rzeczy):
1- (6,6), 2- (2,4), 3- (3,5), 4- (2,7)
5-(3,10), 6-(1,2)
Kryterium najmniejszej wagi- 23 razy rzecz 6
, wartość łączna plecaka 46
Kryterium największej wartości- 7 razy rzecz
5 i jeden raz rzecz 4 – wartość łączna 77
22. Kontrprzykład
Kryterium największego ilorazuwartość/waga – 11 razy rzecz 4 i rzecz 6, co
daje wartość 79
Tymczasem: 10 razy rzecz 4 oraz rzecz 5
wypełniając plecak dają wartość 80, na co
znowu nie wskazuje żadna z proponowanych
strategii zachłannych.
23. Wniosek
dla decyzyjnego oraz ogólnego,dyskretnego problemu pakowania plecaka
nie można w wielu przypadkach uzyskać
rozwiązania optymalnego ze względu na
brak własności wyboru zachłannego
istnienie własności optymalnej podstruktury
daje jednak nadzieje na uzyskanie
rozwiązania tego problemu w ogóle (co
pokażemy w odniesieniu do metody
programowania dynamicznego)
24. Czy nie istnieje wersja problemu plecakowego możliwa do rozwiązania przy użyciu strategii zachłannej ?
istnieje..jest to tzw. ciągły problem plecakowy
dla tego problemu rzeczy mogą występować
także w liczbie ułamkowej (stąd traci sens
podział na problem decyzyjny i ogólny)
to wiele zmienia, bo istnieje wybór
zachłanny –choćby kryterium ilorazu
cena/masa
25. Przykład
Rozważmy plecak o masie m=50Niech n=3, a parametry rzeczy są następujące( w
nawiasie najpierw masa, a potem cena rzeczy):
1- (10,60), 2- (20,100), 3- (30,120)
Wg wybranego kryterium bierzemy rzecz 1, potem
rzecz 2 oraz 2/3 rzeczy 3 co daje wartość 240 –
optymalną.
Zauważmy, że w wariacie ciągłym możliwość
„dopasowania” jaką dają wartości ułamkowe
zawsze da poprawne i optymalne rozwiązanie
problemu. Pozostaje kwestia realistycznego
wykorzystania tego wariantu problemu
plecakowego
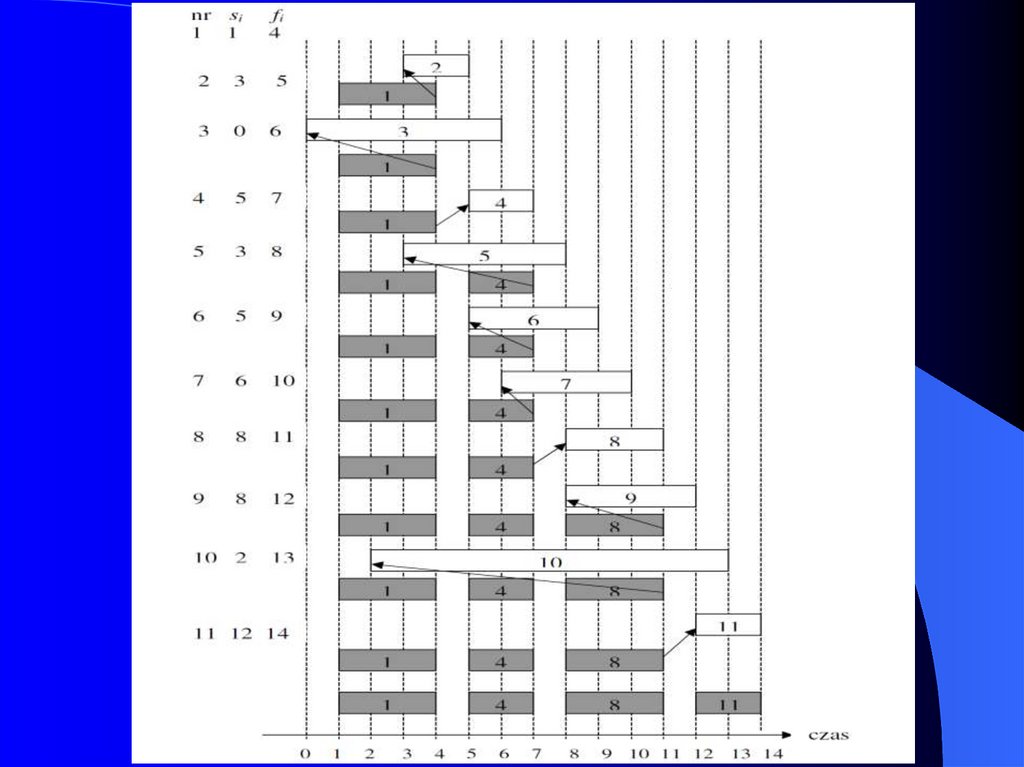
26. Problem wyboru zajęć
Rozważamy zbiór n danych {1,2,..n}stanowiących zajęcia, do których mają być
przydzielone zasoby (np. sala wykładowe).
Zajęcia cechują się czasem rozpoczęcia
si(i=1,2..n) oraz czasem zakończenia
fi(i=1,2..n). Zajęcia dysponują zasobem na
wyłączność tzn. w sali wykładowej w danej
chwili mogą odbywać się tylko jedne zajęcia.
27. Problem wyboru zajęć
28. Problem wyboru zajęć
Należy wybrać spośród wszystkich n zajęcmaksymalnie możliwą liczbę zajęc parami
zgodnych.
29. Problem wyboru zajęć –szkic algorytmu
30.
31. Algorytm Huffmana
algorytm realizuje kompresję danych(oryginalnie tekstów, dziś ma też szersze
zastosowania)
w standardowej reprezentacji danych kod
każdego znaku ma identyczną długość (np.
8 bitów w kodzie ASCII)
jedną z technik kompresji znaków jest
kodowanie częstotliwościowe
32. Kodowanie częstotliwościowe
idea jest taka, żeby znaki pojawiające sięczęściej miały krótszą reprezentację, a
rzadsze mogą mieć nawet dłuższą niż
standardowa – co pozwoli zmniejszyć
wielkość reprezentacji całego tekstu
kandydat na kodowanie częstotliwościowe
–alafabet Morse’a, ale nie był to kod
prefiksowy
kod zaproponowany przez Huffmana jest
prefiksowy
33. Algorytm Huffmana
Dane: częstotliwości występowaniakodowanych znaków (skąd je brać o tym
dalej)
Wynik: kody binarne przydzielone znakom w
oparciu o ideę kodowania
częstotliwościowego
34. Algorytm Huffmana-idea budowania drzewa Huffmana
Rozważmy 5 przykładowych znaków-obokpodano ich częstotliwości:
a- 8.71
d- 3.45
k- 3.10
o- 7.90
r- 4.63
35. Etap I-porządkujemy węzły drzewa wg częstotliwości występowania znaków
k-3.10d-3.45
r-4.63
o-7.90
a-8.71
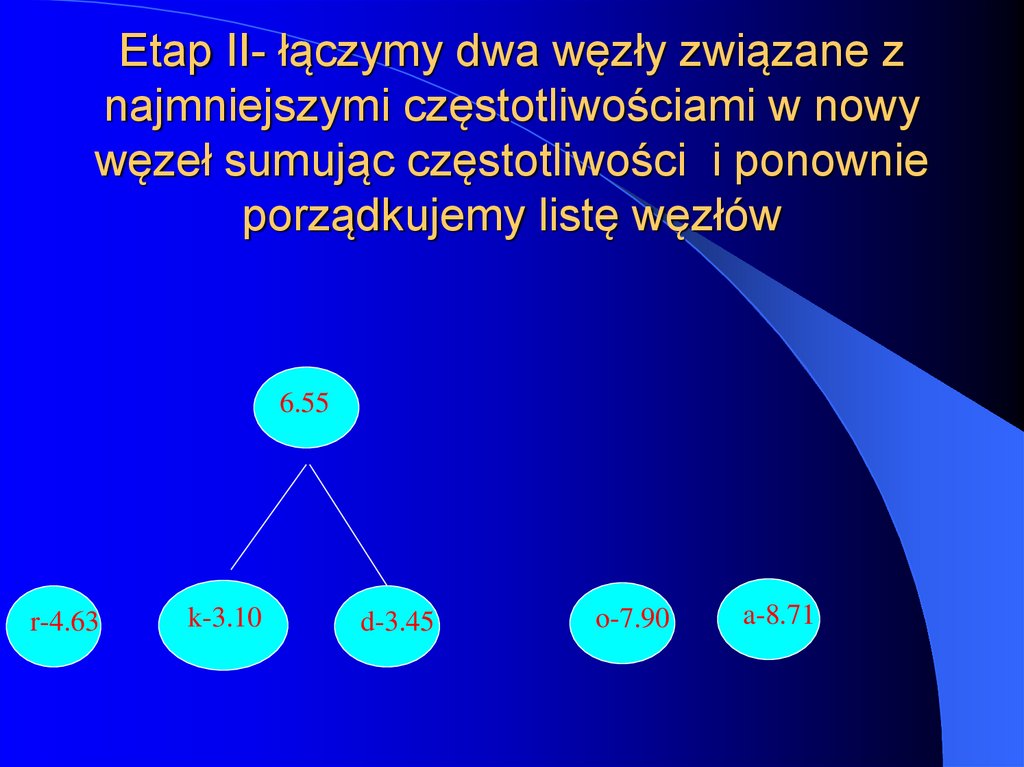
36. Etap II- łączymy dwa węzły związane z najmniejszymi częstotliwościami w nowy węzeł sumując częstotliwości i ponownie
porządkujemy listę węzłów6.55
r-4.63
k-3.10
d-3.45
o-7.90
a-8.71
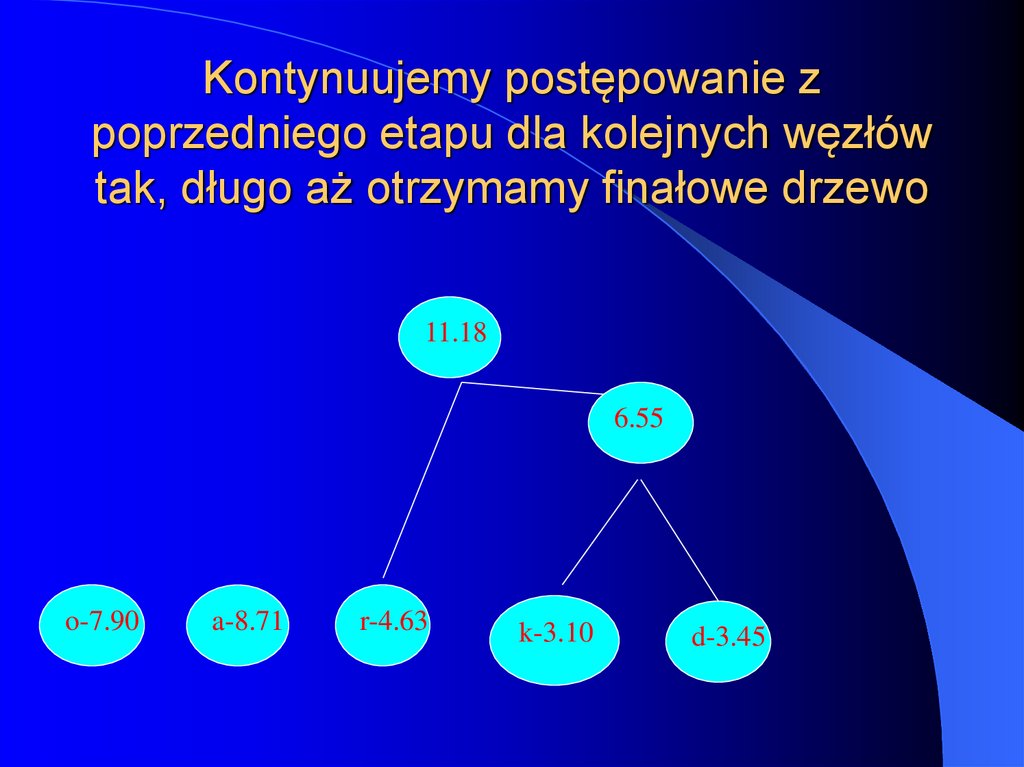
37. Kontynuujemy postępowanie z poprzedniego etapu dla kolejnych węzłów tak, długo aż otrzymamy finałowe drzewo
11.186.55
o-7.90
a-8.71
r-4.63
k-3.10
d-3.45
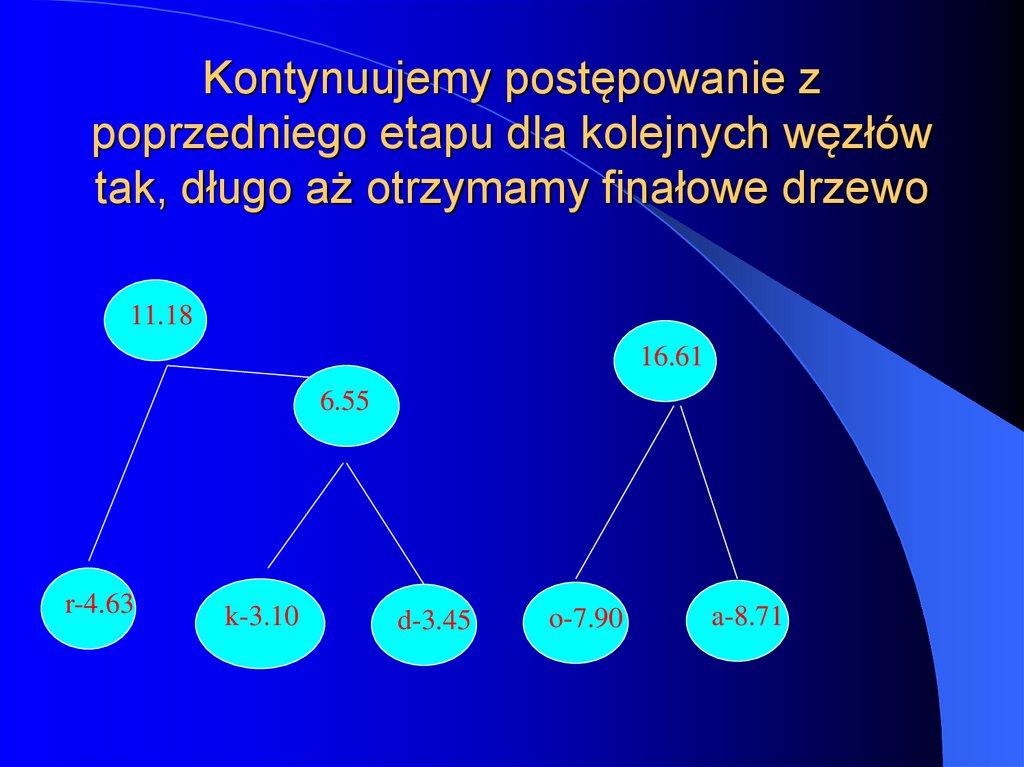
38. Kontynuujemy postępowanie z poprzedniego etapu dla kolejnych węzłów tak, długo aż otrzymamy finałowe drzewo
11.1816.61
6.55
r-4.63
k-3.10
d-3.45
o-7.90
a-8.71
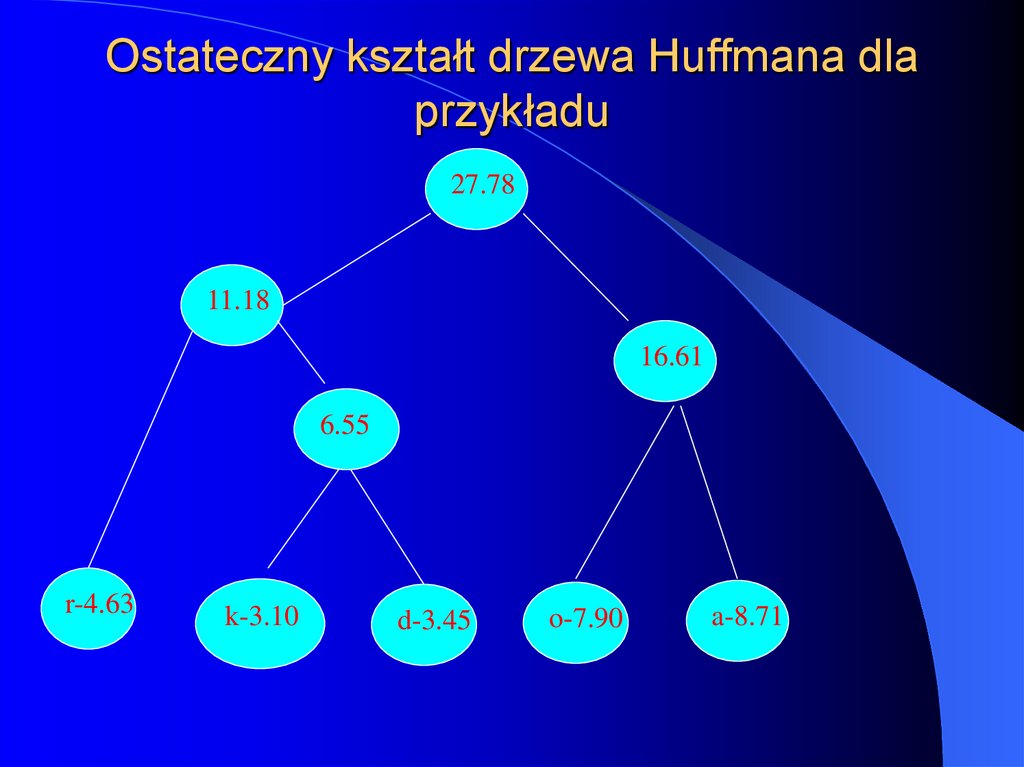
39. Ostateczny kształt drzewa Huffmana dla przykładu
27.7811.18
16.61
6.55
r-4.63
k-3.10
d-3.45
o-7.90
a-8.71
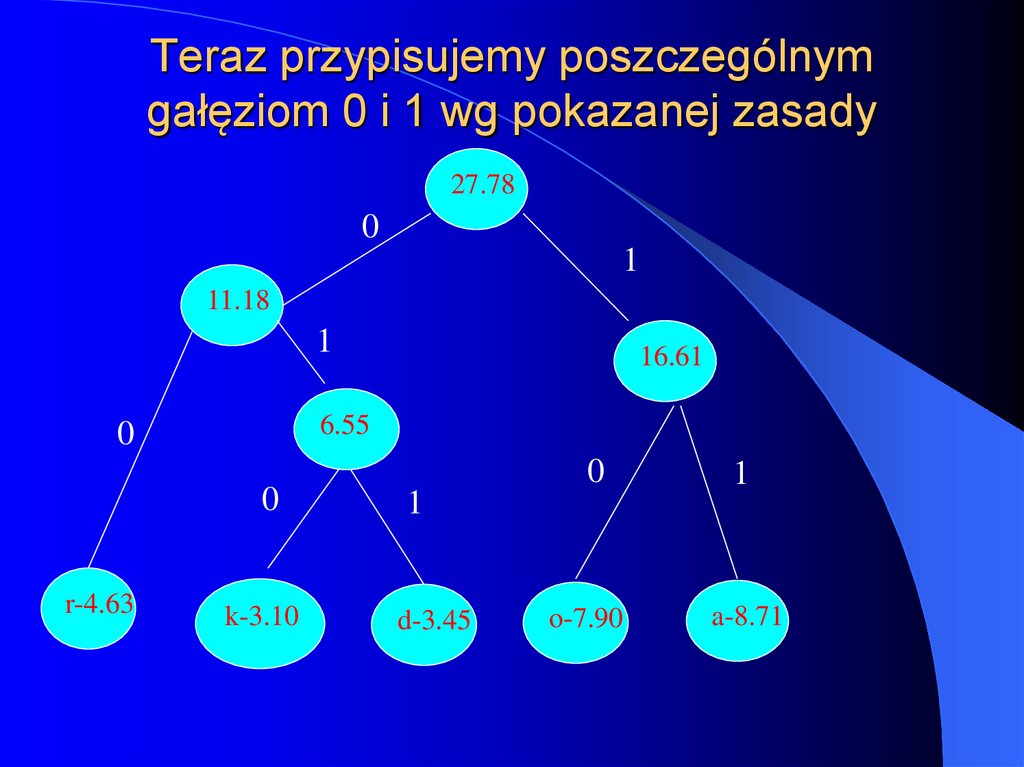
40. Teraz przypisujemy poszczególnym gałęziom 0 i 1 wg pokazanej zasady
27.780
1
11.18
1
6.55
0
r-4.63
16.61
0
1
k-3.10
d-3.45
0
1
o-7.90
a-8.71
41. Ostateczne przypisanie znakom kodów na podstawie drzewa
a- 11d- 011
k- 010
o- 10
r- 00
Kod jest bez wątpienia prefiksowy.
Jakie słowo zakodowano na podstawie
naszego przykładu: 010100011 ?
42. Ważne uwagi uzupełniające
większe zróżnicowanie długości kodu dlaznaków można byłoby zaobserwować dla
większej liczby danych (np. dla całego alfabetu)
kod znaku może być inny zależnie od tego jakie
znaki kodujemy (jakie są dane wejściowe dla
problemu)
częstotliwości niezbędne do tworzenia drzewa
Huffmana można pozyskać na podstawie tekstu
poddanego kompresji (jeśli jest dostatecznie
długi i reprezentatywny) albo z dostępnych tabel
(pochodzących np. z badań językowych)
43. Ważne uwagi uzupełniające
współcześnie algorytm Huffmana jestczęsto wykorzystywany jako etap w
kodowaniu różnych danych
w implementacji algorytmu Huffmana
można wykorzystać struktury drzewiaste
(grafowe)
44. Algorytm Huffmana, a strategia zachłanna
jednoznaczny wybór zachłanny (na każdymkroku wybieramy i łączymy węzły o
najmniejszych częstotliwościach)
zachowana jest też własność optymalnej
podstruktury (na danym etapie mamy
drzewo stworzone z już połączonych
węzłów i tych, które do niego zostaną
dołączone)
45. Przykład problemu trudniejszego-problem szeregowania zadań
Przykład problemu trudniejszegoproblem szeregowania zadańdany jest zbiór n zadań o jednostkowym
czasie realizacji
każde zadanie ma swój nieprzekraczalny
termin realizacji di(i=1,2,…n)
za przekroczenie terminu wykonania każde
zadanie ma swoją indywidualną karę
umowną wi(i=1,2,…n)
Zadanie: ustawić zadania w takiej kolejności,
aby koszt kar umownych był jak najmniejszy
46. Uwagi o strategii zachłannej dla problemu szeregowania zadań
tworzymy porządek, w którym zadaniakończące się w terminie poprzedzają te,
które będą spóźnione (wg kryterium kosztu
kar umownych)
zadania realizowalne w terminie
porządkujemy ze względu na termin ich
ukończenia
47. Strategia zachłanna –uwagi końcowe
warunkiem koniecznym uzyskania poprawnego ioptymalnego rozwiązania przy pomocy tej metody
jest wypełnienie własności wyboru zachłannego
oraz optymalnej podstruktury
poprawność metody uzasadnia się na gruncie
teorii matematycznej związanej z tzw. matroidami
mimo kontrprzykładów dla pierwszych dwóch
problemów (ale one wiązały się z brakiem wyboru
zachłannego co dyskwalifikuje tę strategię w
odniesieniu do tych problemów) jest dostatecznie
dużo zadań, które przy pomocy strategii
zachłannej rozwiązuje się skutecznie









































 lingvistics
lingvistics