Теория вероятностей. Этапы развития

1. Теория вероятностей

Этапы развития

2. Теория вероятностей

Теория вероятностей — раздел математики,
изучающий закономерности случайных явлений:
случайные события, случайные величины, их
свойства и операции над ними.

3.

Теорию вероятностей можно описательно определить как
математическую теорию случайных явлений.
В повседневной жизни мы часто пользуемся словами
"вероятность", "шанс" и т.д. "К вечеру, вероятно, пойдет дождь",
"вероятнее всего, мы на всю неделю поедем в деревню", "это
совершенно невероятно!", "есть шанс, что успешно сдам
экзамен" и т.д. - все эти выражения как-то оценивают
вероятность того, что произойдет некоторое случайное событие.
Вероятность математическая – числовая характеристика степени
возможности появления какого-либо определенного события в
тех
или
иных
определенных,
могущих
повторятся
неограниченное число раз условиях.

4.

Развитие теории вероятностей с момента зарождения
этой науки и до настоящего времени было несколько
своеобразным. На первом этапе истории этой науки
она рассматривалась как занимательный “пустячок”,
как собрание курьезных задач, связанных в первую
очередь с азартными играми в кости и карты.

5.

Возникновение теории вероятностей как науки относят к средним векам и
первым попыткам математического анализа азартных игр (орлянка, кости,
рулетка). Первоначально её основные понятия не имели строго
математического вида, к ним можно было относиться как к некоторым
эмпирическим фактам, как к свойствам реальных событий, и они
формулировались в наглядных представлениях. Самые ранние работы
учёных в области теории вероятностей относятся к XVII веку. Исследуя
прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма
открыли первые вероятностные закономерности, возникающие при
бросании костей.
Блез Паскаль (1623-1662) французский
математик,
физик, литератор и философ.
Пьер де Ферма (1601-1665) французский математик.

6.

Важный вклад в теорию вероятностей внёс Якоб Бернулли: он
дал доказательство закона больших чисел в простейшем случае
независимых испытаний. В первой половине XIX века теория
вероятностей начинает применяться к анализу ошибок
наблюдений; Лаплас и Пуассон доказали первые предельные
теоремы.
Якоб Бернулли (16541705) - швейцарский
математик.
Пьер-Симон
Лаплас
(1749-1827)
французский математик,
физик и астроном.
Симеон-Дени
Пуассон
(1781-1840) - французский
физик и математик.

7.

Во второй половине XIX века основной вклад внесли русские
учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это
время были доказаны закон больших чисел, центральная
предельная теорема, а также разработана теория цепей
Маркова.
Пафнутий
Львович
Чебышев (1821-1894) русский математик и
механик.
Андрей
Андреевич
Марков (1856-1922) выдающийся русский
математик.
Александр Михайлович
Ляпунов (1857-1918) математик и механик.

8.

Современный вид теория вероятностей получила благодаря
аксиоматизации, предложенной Андреем Николаевичем
Колмогоровым. В результате теория вероятностей приобрела
строгий математический вид и окончательно стала
восприниматься как один из разделов математики.
Андрей
Николаевич
Колмогоров
(1903-1987) — выдающийся советский
математик.
Доктор физико-математических наук,
профессор
Московского
Государственного Университета (1931),
академик Академии Наук СССР (1939),
лауреат Сталинской премии, Герой
Социалистического
Труда.
Колмогоров
—
один
из
основоположников современной теории
вероятностей,
им
получены
фундаментальные
результаты
в
топологии, математической логике,
теории
турбулентности,
теории
сложности алгоритмов и ряде других
областей математики и её приложений.

9.

В повседневной речи мы часто используем слова "вероятность",
"случай", "событие". Интуитивно вероятность некоторого
события воспринимается как характеристика возможности его
появления.

10.

Экспериментатор
Бюффон
К.Пирсон
К.Пирсон
Опыты
04 040
12 000
24 000
Выпало гербов
02 048
06 014
12 012
Частота
0.5080
0.5016
0.5006
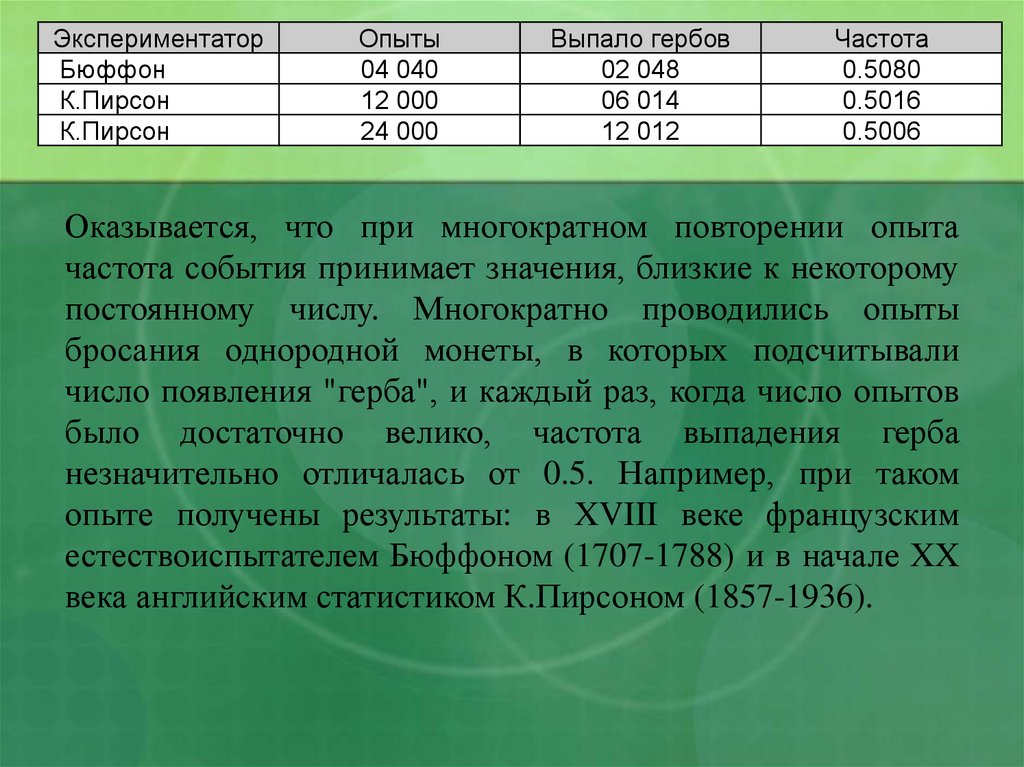
Оказывается, что при многократном повторении опыта
частота события принимает значения, близкие к некоторому
постоянному числу. Многократно проводились опыты
бросания однородной монеты, в которых подсчитывали
число появления "герба", и каждый раз, когда число опытов
было достаточно велико, частота выпадения герба
незначительно отличалась от 0.5. Например, при таком
опыте получены результаты: в XVIII веке французским
естествоиспытателем Бюффоном (1707-1788) и в начале XX
века английским статистиком К.Пирсоном (1857-1936).

11.

Описанное в примере явление, а также неоднократные
наблюдения и других массовых явлений позволяют сделать
вывод, что если опыт повторяется в одинаковых условиях
достаточно большое количество раз, то частота появления
некоторого события колеблется около некоторой постоянной
величины. Так, например, подсчитано что частота рождения
мальчиков составляет 0.518, а девочек 0.482.
Эту постоянную величину, к которой приближается частота
событий, называют вероятностью этого события.

12.

Возникновение и развитие теории вероятностей продиктовано
необходимостью ее применениям, начиная от хозяйственноприкладных вопросов и заканчивая самыми тонкими
теоретическими вопросами теории информации и теории
случайных процессов.