Решение задач. Сириус

1.

Решение задач

2.

Задание №1
Напишите наибольшее целое число x, для которого истинно
высказывание:
НЕ (X <= 11) И НЕ (X >= 17) И (X нечётное)
Решение:
X>11 И X<17 И Х нечётное
Ответ: 15

3.

Задание №2
Известно, что для чисел X, Y и Z истинно высказывание:
(Z<X ∨ Z<Y)∧¬(Z+2<X)∧¬(Z+2<Y)
Чему равно Z, если X=25 и Y=48?
Решение:
(Z<X ∨ Z<Y)∧ ¬(Z+2<X) ∧ ¬(Z+2<Y) =1
Z<25 или Z<48 ⇒ Z<48
¬(Z+2<X)=Z+2>=25 ⇒ Z>=23
¬(Z+2<Y)=Z+2>=48 ⇒ Z>=46
Ответ: 46

4.

Задание №3
Укажите наименьшее целое значение А, при котором выражение
(x > 9) ∨ (x < y) ∨ (x*y < A)
истинно для любых целых положительных значений x и y.
Решение:
(x > 9) ∨ (x < y) ∨ (x*y < A)=1
1 часть «истинна», когда х>9. Если 1 часть «ложь», то проверяем вторую
часть.
2 часть истинна при ложной первой, когда 9<y.
Если 1 и 2 «ложь», то проверяем третью часть.
3 часть 9*9<A. «Истинна», при А=82.
Ответ: 82

5.

Задание №4
Для какого наименьшего целого неотрицательного числа
А выражение:
(y+2x<A) ∨ (2y+x>28) ∨ (4y-x<20)
тождественно истинно, при любых целых неотрицательных x и y ?
Решение:
Если выражение 2 и 3 будет ложно, то 1 должно быть истинным обязательно!
2y+x=28
решаем систему: y=8, x= 12
4y-x=20
Подставляем в первое выражение:
8+2*12<A ⇒ A=33
Ответ: 33

6.

Задание №6
Обозначим через ДЕЛ(n,m) утверждение «натуральное число n делится
без остатка на натуральное число m». Для какого наибольшего
натурального числа А формула ¬ДЕЛ(x,А)→(ДЕЛ(x,6)→ ¬ДЕЛ(x,9))
тождественно истинна (то есть принимает значение 1 при любом
натуральном значении переменной х)?

7.

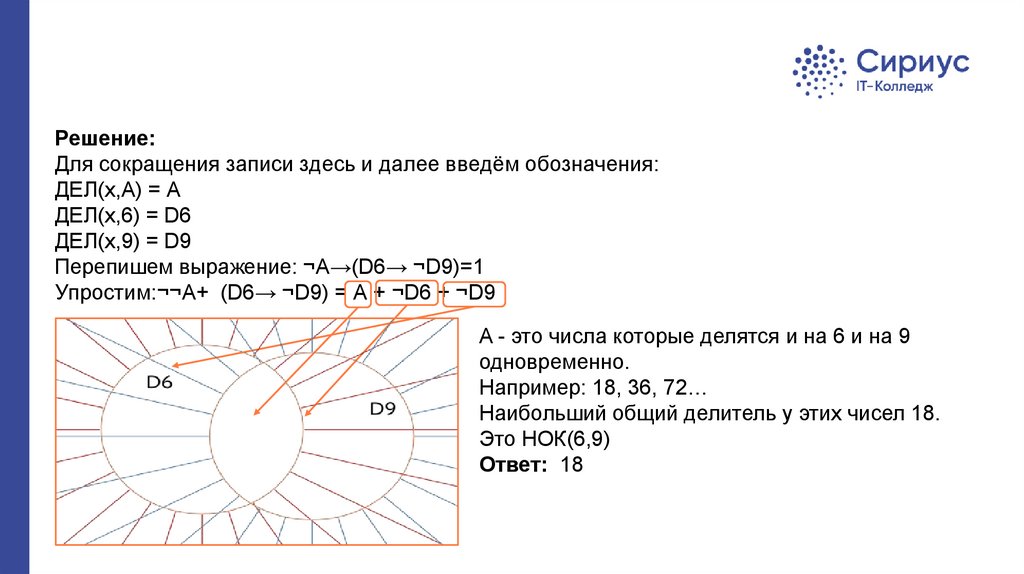
Решение:
Для сокращения записи здесь и далее введём обозначения:
ДЕЛ(x,А) = A
ДЕЛ(x,6) = D6
ДЕЛ(x,9) = D9
Перепишем выражение: ¬А→(D6→ ¬D9)=1
Упростим:¬¬А+ (D6→ ¬D9) = A + ¬D6 + ¬D9
A - это числа которые делятся и на 6 и на 9
одновременно.
Например: 18, 36, 72…
Наибольший общий делитель у этих чисел 18.
Это НОК(6,9)
Ответ: 18

8.

Задание №7
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится
без остатка на натуральное число m». Для какого наименьшего
натурального числа А формула ДЕЛ(x, А) → (ДЕЛ(x, 20) + ДЕЛ(x, 37))
тождественно истинна (то есть принимает значение 1 при любом
натуральном значении переменной х)?

9.

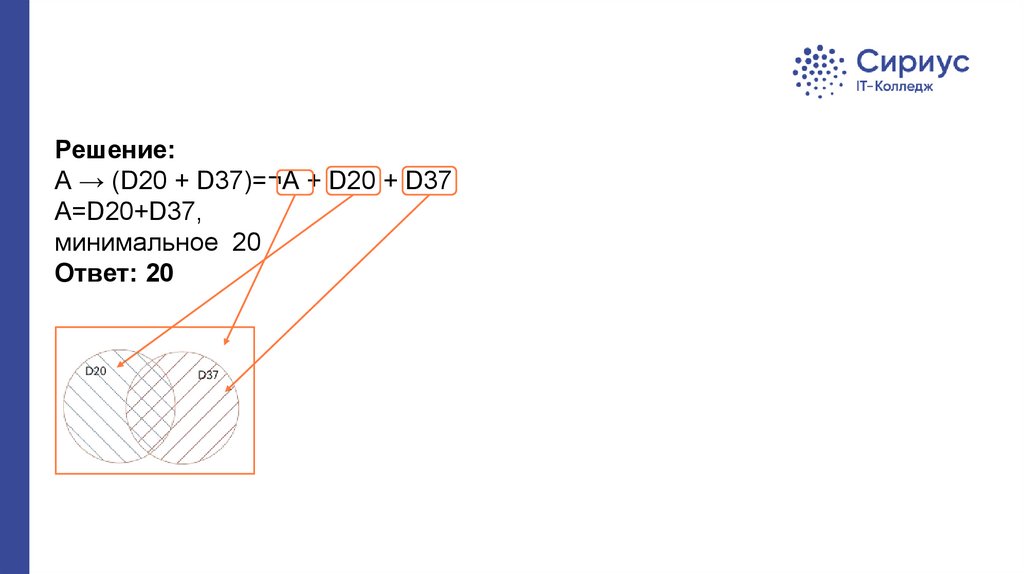
Решение:
А → (D20 + D37)=¬А + D20 + D37
A=D20+D37,
минимальное 20
Ответ: 20

10.

Задание №8
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится
без остатка на натуральное число m». Для какого наибольшего
натурального числа А формула ¬ДЕЛ(x, А)→ (¬ДЕЛ(x, 18) ⋀¬ ДЕЛ(x, 30))
тождественно истинна (то есть принимает значение 1 при любом
натуральном значении переменной х)?

11.

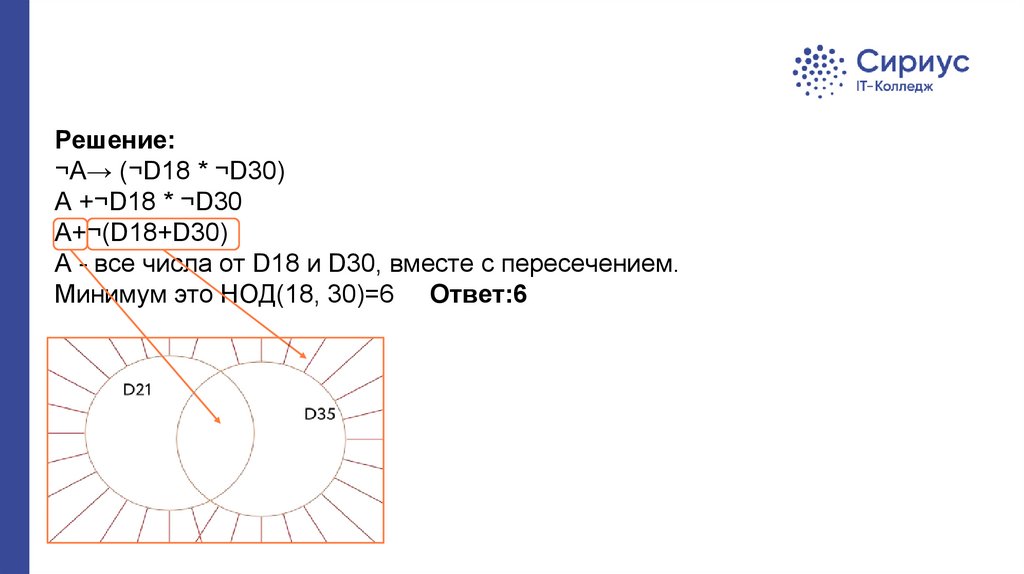
Решение:
¬А→ (¬D18 * ¬D30)
А +¬D18 * ¬D30
A+¬(D18+D30)
A - все числа от D18 и D30, вместе с пересечением.
Минимум это НОД(18, 30)=6 Ответ:6

12.

Задание №9
На числовой прямой даны два отрезка: P=[37; 60] и Q=[40; 77]. Укажите
наименьшую возможную длину такого отрезка A, что формула
(x∈P)→(((x∈Q)⋀¬(x∈A))→¬(x∈P)) тождественно истинна, при любом
значении переменной х.

13.

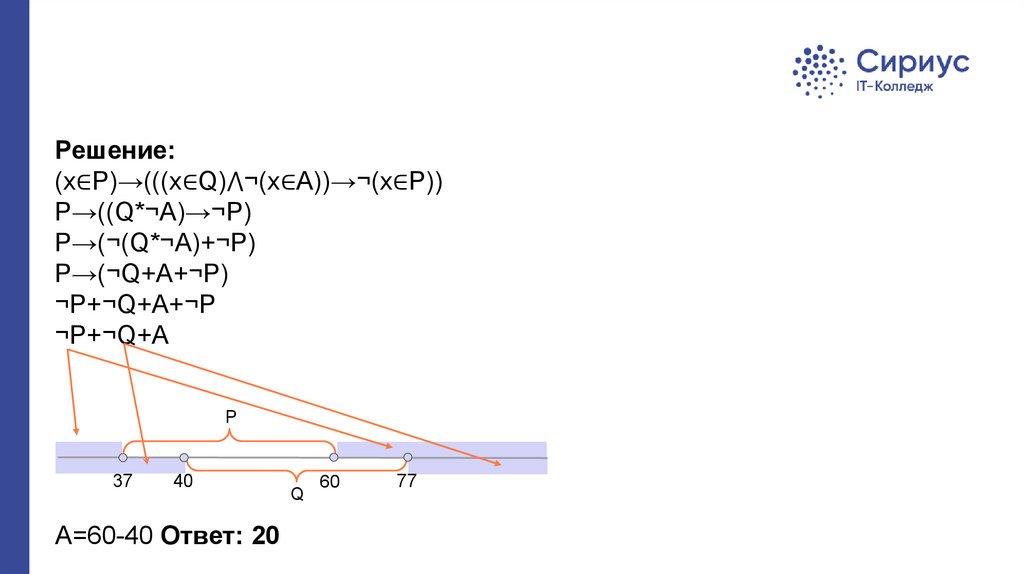
Решение:
(x∈P)→(((x∈Q)⋀¬(x∈A))→¬(x∈P))
P→((Q*¬A)→¬P)
P→(¬(Q*¬A)+¬P)
P→(¬Q+A+¬P)
¬P+¬Q+A+¬P
¬P+¬Q+A
P
37
40
А=60-40 Ответ: 20
Q
60
77

14.

Задание №10
На числовой прямой даны два отрезка: P = [5;30]и Q = [25;55]. Определите
наибольшую возможную длину отрезка A, при котором формула
(x∈A)→((x∈P)∨(x∈Q))тождественно истинна, то есть принимает значение 1
при любом значении переменной х.

15.

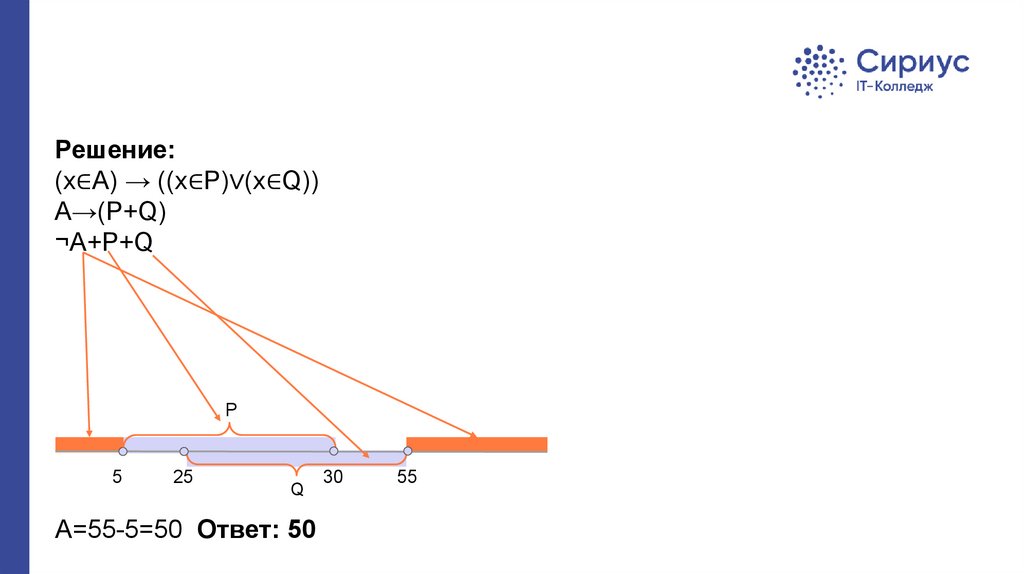
Решение:
(x∈A) → ((x∈P)∨(x∈Q))
A→(P+Q)
¬A+P+Q
P
5
25
Q
A=55-5=50 Ответ: 50
30
55

16.

Задание №13
На числовой прямой даны отрезки A=[70;90], B=[30;80] и C=[0;N] и функция
F(x) = (¬(x∈A)→(x∈B) )∧(¬(x∈C)→(x ∈ A) )
При каком наименьшем числе N функция F(x) истинна более чем для 40
целых чисел x?

17.

Решение:
F(x) = (¬(x∈A)→(x∈B) )∧(¬(x∈C)→(x ∈ A) )
F(x) = (¬A→B )*(¬C→A )
F(x) = (A+B )*(C+A )
F(x) = A+(B*C)
A=(90-70)+1 (т.к. включительно)=21
Нужно еще 19. С 0 до 49 т.к. пересечение В и С
В
0
30
Ответ: 49
?
70
А
80
90