Написание функций. Рекурсия. Сопоставление образцов (лекция 2)

1. Написание функций: Рекурсия. Сопоставление образцов.

Лектор:
доцент каф. АОИ
Салмина Нина
Юрьевна

2. Создание простой функции

Декларация типа
<имя функции> :: <тип арг1> -> <тип арг2> -> <тип результата>
Описание функции
<имя функции> <список аргументов> = <тело функции>
ОДНО выражение!

3. Полиморфные типы

Полиморфные типы – типы, которые универсально
квантифицированы по всем типам.
Полиморфные выражения типа описывают семейства типов.
Например, [a] – семейство типов состоит из типов списков,
элементы которых принадлежат фиксированному типу а
Здесь а – идентификатор типа аргумента, который можно
привязать к различным типам, в зависимости от
использования ([a] – может быть списком целых, списком
символов, списком списков целых и т.п.)
rev :: [a] -> [a]
-- функция будет работать со
-- списками любого типа

4. Полиморфные типы (продолжение)

У функции может быть несколько аргументов типа, каждый из
них будет получать свое значение независимо от других.
f :: [a] -> [a] -- список, подаваемый на вход функции, и список,
-- возвращаемый в качестве значения функции,
-- имеют элементы одного типа
ff :: [a] -> [b] -- входной и результирующий списки могут
-- содержать элементы разных типов

5. Рекурсивные функции

Рекурсивная функция - если во время выполнения ее тела
может встретиться обращение к этой функции.
Обращение функции к себе самой – прямая рекурсия.
Если в теле функции f есть обращение к функции f1, а в
теле f1 — обращение к f2, ..., а в теле fn — обращение к
f, то рекурсия называется косвенной.
1. Терминальная ветвь (правило окончания) необходима для
окончания вызова: возвращает результат.
Желательно: сначала
окончания, а затем
вычислений.
2. После
проверять всевозможные условия
ситуации, требующие продолжения
каждого рекурсивного вызова мы должны
приближаться к терминальной ветви: должна быть
уверенность, что рекурсивные вызовы ведут к терминальной
ветви.

6. Как писать рекурсивные функции

1. Планирование терминальной ветви.
При написании рекурсивной функции мы должны решить,
когда функция может вернуть значение без рекурсивного
вызова.
2. Планирование рекурсивной ветви.
В этом случае мы вызываем функцию рекурсивно с
упрощенным аргументом и используем результат для
расчета значения при текущем аргументе.
Таким образом мы должны решить:
1. Как упрощать аргумент, приближая его шаг за шагом к
конечному значению.
2. Кроме этого необходимо построить форму, называемую
рекурсивным отношением, которая связывает правильное
значение текущего вызова со значением рекурсивного
вызова.

7. Пример 1

Необходимо написать функцию, подсчитывающую
количество элементов в списке s.
Отметим два факта:
1. Если список пуст, количество элементов равно 0.
2. Иначе s равно количеству элементов в хвосте
списка плюс 1.

8. Пример 1

Необходимо написать функцию, подсчитывающую
количество элементов в списке s.
Отметим два факта:
1. Если список пуст, количество элементов равно 0.
2. Иначе s равно количеству элементов в хвосте
списка плюс 1.
leng :: [a] -> Integer
leng x = if null x then 0 else 1 + leng (tail x)

9. Как работает рекурсивная функция

leng x = if null x then 0 else 1 + leng (tail x)
Здесь if – терминальная ветвь, else – рекурсивная
Работа:
(leng [2,45,1]) вызывает (leng [45,1])
(leng [45,1]) вызывает (leng [1])
(leng [1]) вызывает (leng [ ]).
После того как (leng [ ]) вернет 0,
(leng [1]) вернет
0 + 1 = 1,
(leng [45,1]) вернет
1 + 1 = 2,
(leng [2,45,1]) вернет
2 + 1 = 3.

10. Недостатки конструкции if

1.
Может быть несколько терминальных
ветвей
(Ветвь 1. Цель найдена и надо вернуть ответ
Ветвь 2. Цель не найдена и нет больше
элементов)
2.
Может быть несколько рекурсивных
ветвей
(Несколько вариантов обработки данных)

11. Сопоставление с образцами

Функция – в виде последовательности уравнений
Каждое уравнение соответствует подходящему
шаблону аргументов.
Уравнения проверяются последовательно (сверху
вниз) до первого успешного сопоставления: как
только фактическое значение аргумента можно
сопоставить с образцом, проверка останавливается
и значением функции является результат решения
выбранного уравнения (оставшиеся уравнения не
рассматриваются).

12. Сопоставление с образцами

Функция – в виде последовательности уравнений
Каждое уравнение соответствует подходящему
шаблону аргументов.
Пример 1 (вариант с сопоставлением образцов):
leng [ ] = 0
leng (_ : xs) = 1 + leng (xs)

13. Сопоставление с образцами (ограничения)

Формальный параметр (переменная) может
присутствовать в образце не более одного раза в
одном уравнении!
Нельзя написать:
member x (x : ys) = …
Можно:
member x (y : ys) | x == y = …
предохранитель

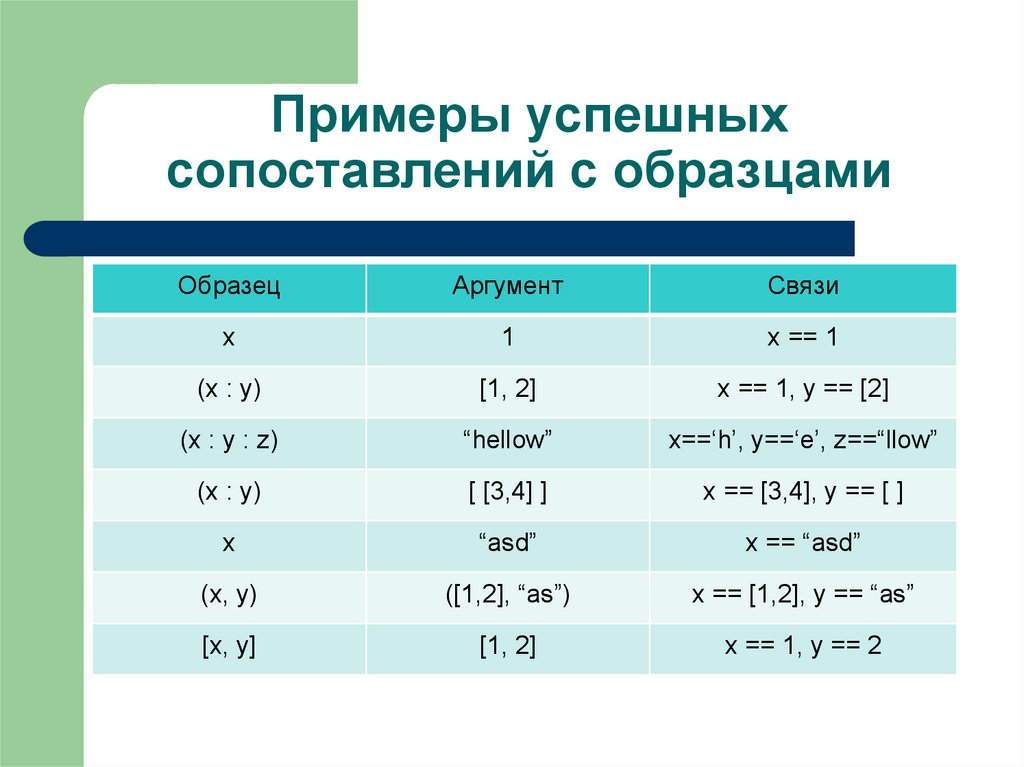
14. Примеры успешных сопоставлений с образцами

Образец
Аргумент
Связи
x
1
x == 1
(x : y)
[1, 2]
x == 1, y == [2]
(x : y : z)
“hellow”
x==‘h’, y==‘e’, z==“llow”
(x : y)
[ [3,4] ]
x == [3,4], y == [ ]
x
“asd”
x == “asd”
(x, y)
([1,2], “as”)
x == [1,2], y == “as”
[x, y]
[1, 2]
x == 1, y == 2

15. Пример 2: вычисление факториала

Функция fact вычисляет факториал n.
Составим рекурсивную таблицу.
Шаг 1. Завершение (Терминальная ветвь)
n=0 - аргумент
fact 0 = 1 - значение
Шаг 2. Рекурсивная ветвь
2а. Упрощение аргумента: уменьшая n на каждом шагу на 1,
мы приближаемся к 0: ( n - 1 )
2б. Характеристическое рекурсивное отношение
fact n может быть получена из
fact ( n - 1) умножением на n

16. Пример 2. Функция fact

fact :: Integer -> Integer
fact 0 = 1
fact n = n * fact ( n – 1)

17. Пример 3. Функция list-sum

Написать функцию list-sum, которая берет
один аргумент, список чисел, и
возвращает сумму этих чисел.
Последовательно упрощающимся
аргументом в этом случае будет список.
Упрощение списка (tail lis).
Последнее значение аргумента [ ].

18. Пример 3. Рекурсивная таблица для list-sum

(list-sum lis)
Шаг 1. Завершение (Терминальная ветвь)
list-sum [ ] = 0 – значение: если список пуст,
сумма его элементов равна 0
Шаг 2. Рекурсивная ветвь
list-sum lis может быть получена из
(суммы элементов из хвоста списка)
сложением с головой списка
представим lis == x : xs

19. Пример 3. Функция list-sum

list-sum :: [Int] -> Int
list-sum [ ] = 0
list-sum (x : xs) = x + list-sum xs

20. Предохранители

Предохранитель – часть синтаксиса сопоставления с
образцом, позволяющая с помощью булевых
условий уточнить образец
<имя функции> х1 х2 … | <логич.выражение> = <тело>
х1,х2 – аргументы функции
Если логическое выражение Истина – выполняется тело,
если Ложь – переходим к следующему предложению

21. Пример 4. Функция greaternum

Два аргумента : список чисел и заданное
число.
Функция возвращает первое число в списке,
превышающее заданное. Если этого числа
нет - возвращается заданное число.

22. Пример 4. Рекурсивная таблица для greaternum

greaternum lis num
Шаг 1. Завершение
Терминальная ветвь 1
greaternum [ ] num = num – возвращает заданное
число (список пуст – не нашли числа больше num)
Терминальная ветвь 2 (lis == x : xs)
если x > num => x – возвращает голову списка
(нашли число больше num)
Шаг 2. Рекурсивная ветвь
Рекурсивные отношения между
greaternum (x : xs) num и greaternum xs num

23. Пример 4. Функция greaternum

greaternum :: [Int] -> Int -> Int
greaternum [ ] num = num
greaternum (x : xs) num | x > num = x
greaternum (_ : xs) num = greaternum xs num

24. Предохранители: проверка нескольких условий

Можно осуществлять проверку нескольких
условий для одного и того же аргумента.
Например:
ff n | n == 2 = …
| n == 3 = …
|n<0 =…
| otherwise = …
Можно использовать where:
f xy |y>z =…
| y == z = …
|y<z =…
where z = x*x

25. Пример 5. Возведение в степень

Необходимо написать функцию возведения в степень (степень
может быть как положительной, так и отрицательной).
step :: Float -> Int -> Float
step _ 0 = 1
step x n | n > 0 = x * step x (n-1)
step x n = step x (n+1) / x

26. Пример 5. Возведение в степень

Необходимо написать функцию возведения в степень (степень
может быть как положительной, так и отрицательной).
step :: Float -> Int -> Float
step _ 0 = 1
step x n | n > 0 = x * step x (n-1)
step x n = step x (n+1) / x
Другой вариант
step x n | n==0 = 1
| n > 0 = x * step x (n-1)
| n < 0 = 1 / (step x (-n))

27. Пример 6

Благодаря сопоставлению с образцом терминальная ветвь
может быть записана после рекурсивной!
Задача: удалить в списке повторяющиеся подряд идущие
элементы.
rem_d :: [a] -> [a]
rem_d (x : y : xs) | x==y = rem_d (y : xs)
| x/=y = x : rem_d (y : xs)
rem_d xs = xs

28. Именованные образцы Пример 6 (продолжение)

Весь образец, которому мы хотим дать имя, заключить в
скобки, перед скобками указать переменную и символ @
rem_d (x : q@(y : _)) | x==y = rem_d q
| x/=y = x : rem_d q
rem_d xs = xs

29. Кортежи

Кортеж – тип данных, который является набором фиксированного
количества разнородных элементов. Элементы кортежа
заключаются в круглые скобки и разделяются запятыми:
q5 :: (Int, [Char], Float)
q5 = (3, "asd", 3.5)
q6 :: ([Int], Int, String)
q6 = ([1,2,3], 34, “Ivanov")
*Main> q5
(3,"asd",3.5)
*Main> q6
([1,2,3], 34, “Ivanov")

30. Встроенные функции для работы с кортежами

fst - аргументом является двуместный кортеж, возвращает первый
компонент кортежа.
fst :: (a, b) -> a
snd - аргументом является двуместный кортеж, возвращает второй
компонент кортежа.
snd :: (a, b) -> b
Кортеж может содержать компоненты любых типов, причем типы
компонентов могут различаться:
> fst (1,2)
1
> fst ([3,2], “abc”)
[3,2]

31. Пример 7

Написать функцию, на вход которой подается фамилия человека, его
дата рождения и текущая дата. Функция должна возвращать кортеж
из фамилии и возраста человека.
age :: (Int,Int,Int) -> (Int,Int,Int) -> Int
age (x1,y1,z1) (x2,y2,z2) | y1 > y2 = z2-z1-1
| y1 < y2 = z2-z1
| x1 > x2 = z2-z1-1
| otherwise = z2-z1
age_person :: [Char] -> (Int,Int,Int) -> (Int,Int,Int) -> ([Char],Int)
age_person x d1 d2 = (x, age d1 d2)
> age_person “ivanov" (9,10,1960) (28,1,2023)
(“ivanov",62)

32. Синонимы типов

Для часто используемых типов можно определить
синонимы, которые создаются декларацией типа:
type String = [Char]
type Date = (Int, Int, Int)
Тогда для предыдущего примера типизация функций:
age :: Date -> Date -> Int
age_person :: String -> Date -> Date -> (String, Int)

33. Типы, определяемые пользователем

Декларация данных: data
Перечислимые типы (конечное число нульарных конструкторов данных):
data Color = Red | Green | Blue | Yellow
-- четыре величины
Полиморфный тип с одним конструктором
Color, Point – имена типов
data Point a = Pt a a
Red, Green, Pt – конструкторы
данных
Примеры:
e1 :: Color
e3 :: Point Float
e1 = Red
e3 = Pt 2.0 3.0
e2 :: [Color]
e4 :: Point (Point Int)
e2 = [Red, Blue]
e4 = Pt (Pt 1 2) (Pt 3 4)

34. Типы, определяемые пользователем

Декларация данных: data
Перечислимые типы (конечное число нульарных конструкторов данных):
data Color = Red | Green | Blue | Yellow
-- четыре величины
Полиморфный тип с одним конструктором
Color, Point – имена типов
data Point a = Pt a a
Red, Green, Pt – конструкторы
данных
Примеры:
e1 :: Color
e3 :: Point Float
e1 = Red
e3 = Pt 2.0 3.0
e2 :: [Color]
e4 :: Point (Point Int)
e2 = [Red, Blue]
e4 = Pt (Pt 1 2) (Pt 3 4)
> e1
Ошибка!
> e3
Ошибка!

35. Типы, определяемые пользователем

Выражение deriving Show
дает возможность печатать значения новых типов:
Примеры:
data Color = Red | Green | Blue | Yellow deriving Show
data Point a = Pt a a deriving Show
e1 :: Color
e3 :: Point Float
e1 = Red
e3 = Pt 2.0 3.0
e2 :: [Color]
e4 :: Point (Point Int)
e2 = [Red, Blue]
e4 = Pt (Pt 1 2) (Pt 3 4)
> e1
Red
> e4
Pt (Pt 1 2) (Pt 3 4)

36. Пример 8 (с использованием пользовательских типов)

Функция, определяющая расстояние между двумя точками.
dist1 :: Point Float -> Point Float -> Float
dist1 (Pt x1 y1) (Pt x2 y2) = sqrt ((x1 – x2)^2 + (y1 – y2)^2)
Функция, определяющая середину отрезка.
dist2 :: Point Float -> Point Float -> Point Float
dist2 (Pt x1 y1) (Pt x2 y2) = Pt ((x1 + x2)/2) ((y1 + y2)/2)
> dist1 (Pt 1.0 1.0)(Pt 2.0 2.0) -- можно: dist1 (Pt 1 1) (Pt 2 (1+1))
1.4142135