Прикладная механика. Лекция 2

1.

Прикладная механика
Лекция 2
1

2.

Тема 2. Растяжение-сжатие.
Центральным растяжением (или сжатием) называется такой вид деформации, при
котором в поперечных сечениях бруса возникает отличный от нуля только один внутренний
силовой фактор – продольная сила, а все остальные внутренние силовые факторы равны нулю.
Это бывает в случаях, когда линия действия равнодействующей внешних сил совпадает с
продольной осью стержня.
Правило знаков: растягивающие продольные силы принято считать положительными, а
сжимающие – отрицательными.
Для определения величины продольной силы N используется метод сечений. При этом
полученное в результате положительное значение N соответствует растягивающей продольной
силе, а отрицательное – сжимающей.
На эпюрах проставляют значения найденных продольных сил, их знак и наносят штриховку
перпендикулярно оси бруса.
Из анализа эпюры N вытекает следующее правило ее проверки: в поперечных сечениях
бруса, в которых приложены внешние активные (F) или реактивные (R) силы, на эпюре
продольных сил возникают скачки, равные по величине этим нагрузкам.
При использовании приведенного выше метода сечений необходимо иметь ввиду: если
рассматривается равновесие части бруса, включающей в себя опорные связи, необходимо
предварительно определить реакции опор, так как они относятся к разряду внешних сил.
2

3.

Внешними признаками границ грузовых участков являются: места приложения внешних
сосредоточенных усилий, места начала или окончания действия распределенной нагрузки, места
изменения интенсивности распределенной нагрузки, в случае учета собственного веса бруса – места резкого изменения площади поперечного сечения.
Для определения нормальных напряжений пользуются гипотезой плоских сечений Бернулли:
сечения плоские и нормальные к продольной оси бруса до деформации, остаются плоскими и
нормальными к этой оси и после деформации.
Продольная сила N равномерно распределена по сечению, вызывая нормальные напряжения
N
н н
, 1 a 2 1 , H , 12M a 1 H ,
A
м м 2 мм
мм 2
1M a 10 6 a
где А - площадь поперечного сечения бруса.
2.1 Продольные и поперечные деформации. Коэффициент Пуассона.
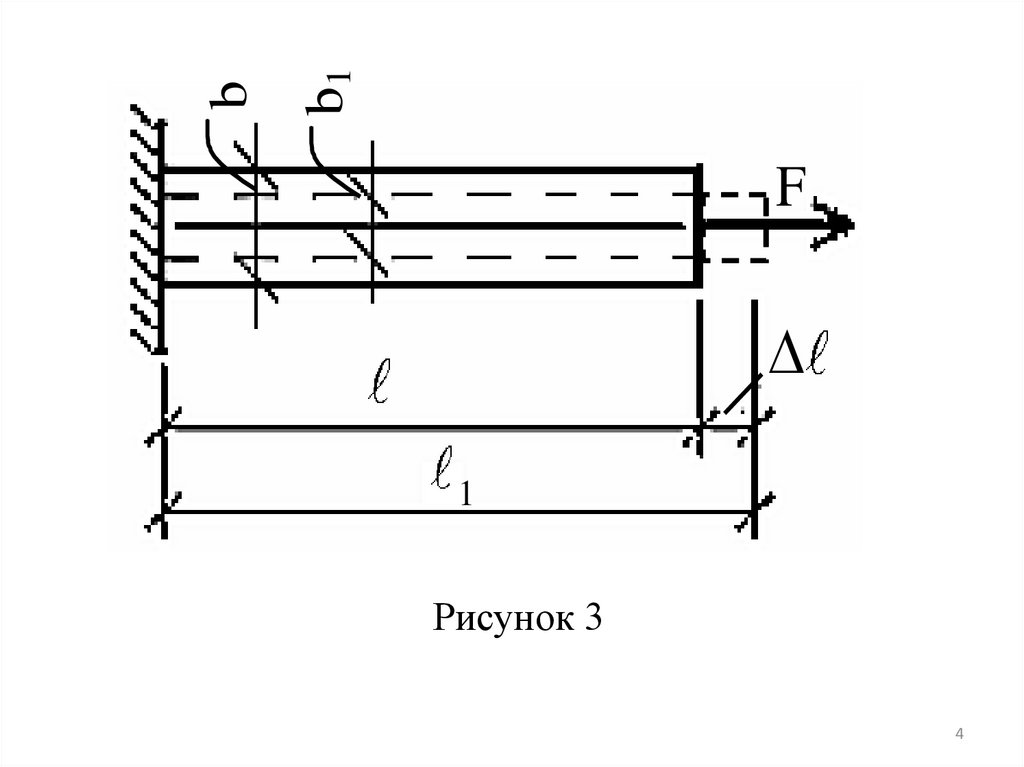
Под действием силы F брус длиной удлиняется на величину , которую называют полным
или абсолютным удлинением (при сжатии – укорочением) (рис.3).
3

4.

b
b1
F
1
Рис.Рисунок
3.4 3
4

5.

Из рисунка 3
l l1 l [м].
При растяжении l >0, при сжатии l < 0.
Так как согласно гипотезе плоских сечений Бернулли по всей длине в любой точке
поперечного сечения бруса возникают одинаковые удлинения то и линейные деформации будут
одинаковы и равны
l
.
l
При растяжении (или сжатии) бруса меняются и его поперечные размеры. Из рис.3
абсолютное сужение бруса:
b b b1 [м].
Относительная поперечная деформация:
'
b
b
.
В пределах применимости закона Гука при растяжении (сжатии) поперечная деформация
прямо пропорциональна продольной деформации , но имеет обратный знак:
' .
Коэффициент называется коэффициентом Пуассона. На основании формулы (2.10)
принимают:
' .
5

6.

В 1660 г. Р. Гук вывел закон, который в настоящее время формулируется так:
деформация прямо пропорциональна вызвавшему ее напряжению, т.е.
или Е ; Е н .
м2
Е
Величину Е называют модулем продольной упругости (модулем Юнга). Это
физическая величина постоянная материала, характеризующая его упругость.
2.2 Определение абсолютной деформации участка бруса
Если связать между собой и , то получим выражения:
N
.
A E
Отсюда формула для определения абсолютного удлинения (или укорочения) участка
стержня длиной :
N
.
E A
В формуле произведение Е А называется жесткостью бруса при растяжении или
сжати.
Диаграмма растяжений
Диаграмма напряжений
Рассмотрим цилиндрический образец в захватах разрывной
машины. Пусть образец выполнен из малоуглеродистой стали.
6

7.

7

8.

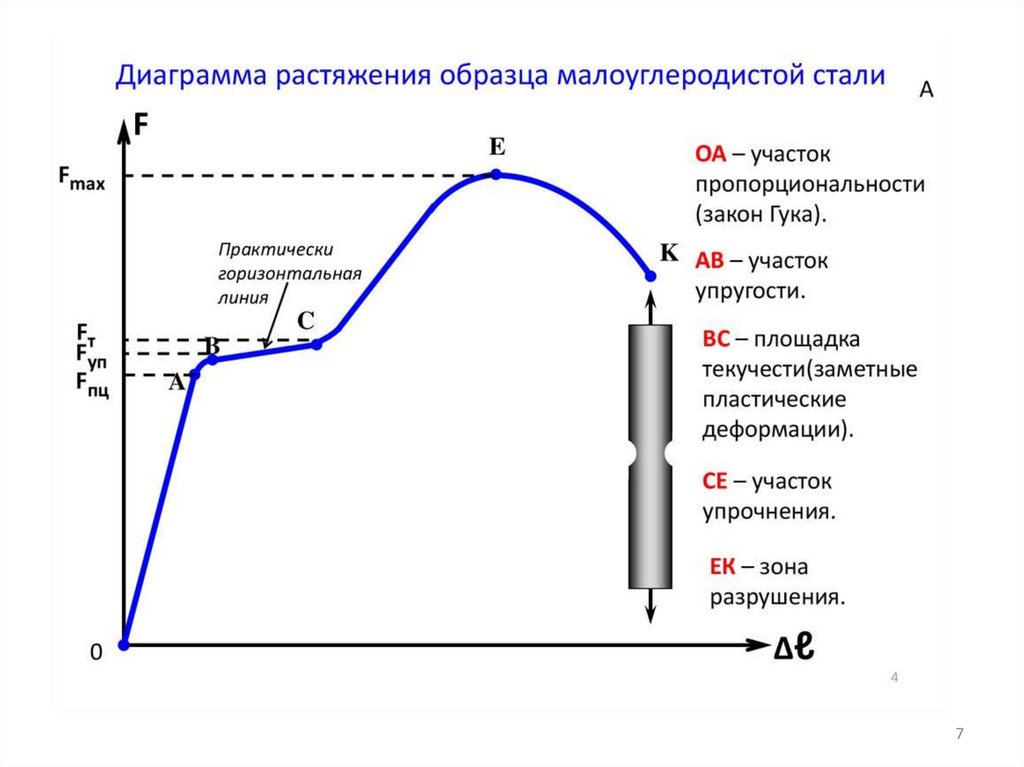
На участке О-А выполняется закон Гука, деформации
пропорциональны нагрузкам (прямая линия).
На участке А-В область упругих деформаций. Если
прервать испытание до точки В, то образец вернется к
исходным размерам. После точки В при продолжении
испытаний образец не возвращается к исходному состоянию.
Участок В-С – площадка текучести. На этом участке
происходит рост деформация без увеличения нагрузки.
Точка Е соответствует максимальной нагрузке. Здесь
наблюдается временное сопротивление разрыву. Образуется
«шейка», после продолжения испытания происходит
разрушение образца.
В точке К происходит разрыв образца. Здесь наблюдается
истинное значение силы при разрыве.
8

9.

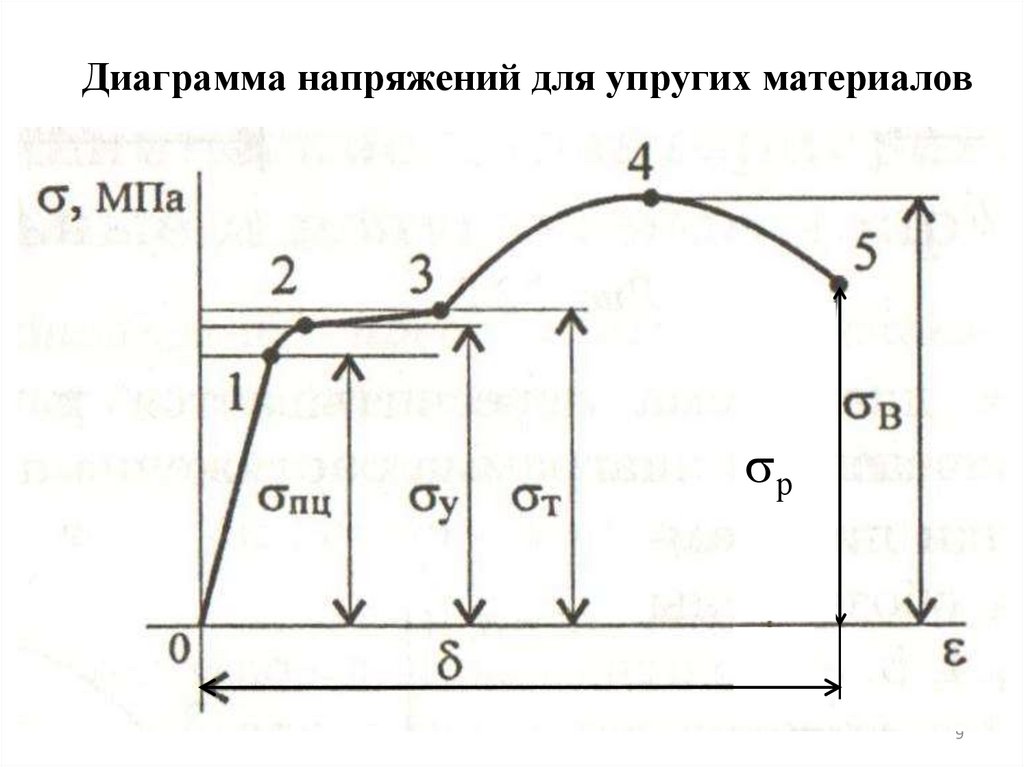
Диаграмма напряжений для упругих материалов
р
9

10.

Достоинства и недостатки стали как
конструкционного материала
Достоинства:
Недостатки:
10

11.

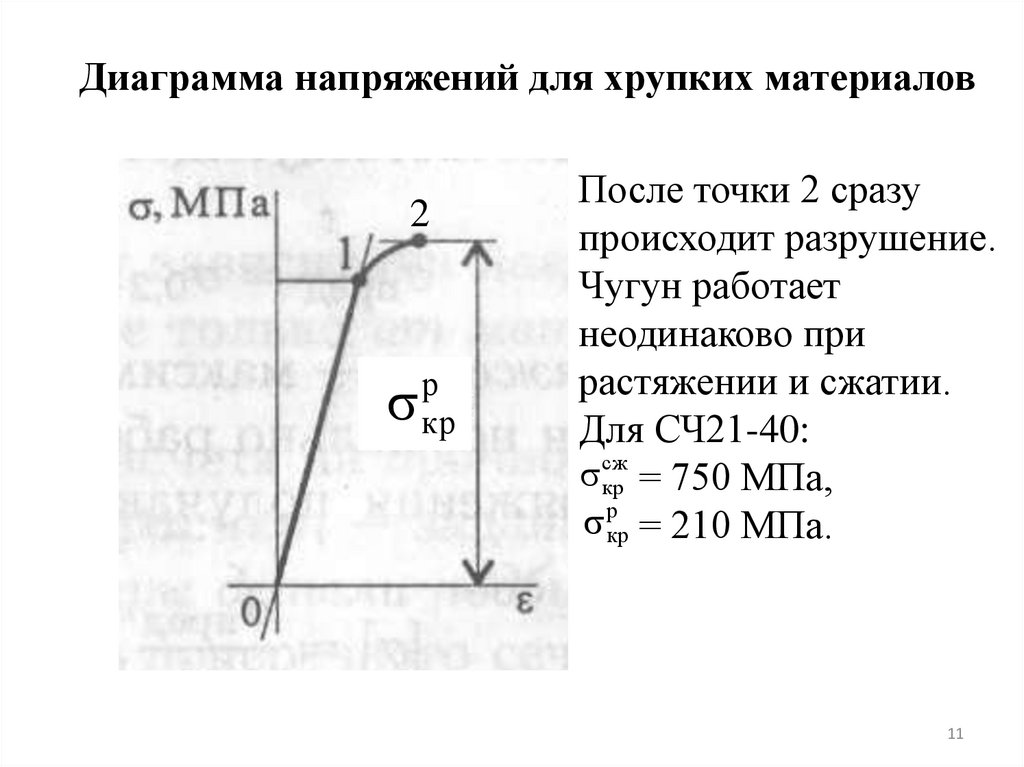
Диаграмма напряжений для хрупких материалов
2
р
кр
После точки 2 сразу
происходит разрушение.
Чугун работает
неодинаково при
растяжении и сжатии.
Для СЧ21-40:
сж
кр = 750 МПа,
р
кр
= 210 МПа.
11

12.

12

13.

2.3 Условие прочности. Подбор сечений.
Расчет на прочность бруса на растяжение и сжатие выполняется по опасной точке, т.е.
нарушением прочности конструкции считают возникновение хотя бы в одной точке предельных
напряжений ПР , при которых в пластичном материале возникают заметные остаточные
деформации, а в хрупком материале – первые признаки разрушения. Для пластичного материала
при статическом нагружении принимают ПР Т (предел текучести), а для хрупкого - ПР В
(предел прочности).
Для того чтобы конструкция была прочной, наибольшее расчетное значение max в ней не
должно превышать предельного
max .
ПР
Это выражение иногда называют физическим условием прочности. Для надежной работы
конструкция должна обладать определенным запасом надежности, запасом прочности, т.к.
фактические нагрузки и свойства материала реально могут существенно отличаться от принятых
для расчета. Для обеспечения надежности конструкции вводят коэффициент запаса прочности,
равный отношению предельного напряжения к расчетному напряжению.
Расчетный запас прочности должен быть не ниже допускаемого, условие прочности имеет
вид
n ПР n .
max
Или
max .
Это выражение называют: условием прочности по нормальным напряжениям.
13

14.

2.4 Расчет на прочность при растяжении (сжатии)
Условие прочности по нормальным напряжениям также записывают в виде:
N
max .
A
Это выражение называют условием прочности на растяжение и сжатие.
Условие прочности должно быть составлено для опасного сечения. Если оно для этого
сечения выполняется, то тем более будет выполнятся для всех остальных сечений.
Опасное сечение – сечение, в котором напряжения наиболее близки к предельным, т.е.
принимают наибольшие значения - max .
Пользуясь данным условием, можно решать следующие задачи:
1. Проверочный расчет: определяют по заданным нагрузкам и размерам поперечного сечения
расчетные напряжения N / А и сравнивают их с допускаемыми . При этом фактические
напряжения не должны отклоняться от допускаемого более чем на 5%, т.е.
100% 5% . - при перегрузке, при недогрузке
допускается 20%
2. Проектировочный расчет: по известным нагрузке и допускаемому напряжению определяют
размеры поперечного сечения бруса по формуле
N .
А
3. Определение допускаемой нагрузки по известным размерам поперечного сечения бруса и
допускаемому напряжению находят
N А .
После определения внутренней продольной силы N устанавливают методом сечений ее связь
с внешней нагрузкой, т.е. определяют ее допускаемое значение.
14