Золотое сечение и где оно присутствует?

1. Золотое сечение и где оно присутствует?

учитель математики
Денцова А.В.

2. Содержание

Введение
Цели и задачи исследования
Рассказ о золотом сечении
Доказательства фактов о золотом
сечении (с аргументами)
• Вывод

3. Введение

• На уроках математики, разбирая тему
пропорции, нас заинтересовала
Божественная пропорция или как ее
еще называют: Золотое сечение.
• Мы захотели прикоснуться к этой
красоте, разобраться и исследовать
данную тему.

4. Цели и задачи

• Узнать, что такое золотое сечение?
• Узнать, где оно присутствует?
• Попытаться найти золотое сечение в
нашем городе.
• Прочитать литературу.
• Провести исследование.
• Сделать выводы.

5. ЗОЛОТОЕ СЕЧЕНИЕ - ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ

ЗОЛОТОЕ СЕЧЕНИЕ ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ
В математике пропорцией называют
равенство двух отношений: a : b = c : d.
Отрезок прямой АВ можно разделить на две
части следующими способами:
- на две равные части - АВ : АС = АВ : ВС;
- на две неравные части в любом отношении
(такие части пропорции не образуют);
- таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление.

6. Золотое сечение.

Золотое сечение – это такое
пропорциональное деление отрезка на
неравные части, при котором весь отрезок
так относится к большей части, как сама
большая часть относится к меньшей; или
другими словами, меньший отрезок так
относится к большему, как больший ко
всему с:b=b:а или a:b=b:c .

7. История

:
История
Представление о золотых пропорциях
имели древние египтяне, знали о них и на
Руси, но впервые научно золотое сечение
объяснил монах Лука Пачоли в книге
«Божественная пропорция» (1509),
иллюстрации к которой предположительно
сделал Леонардо да Винчи. Пачоли
усматривал в золотом сечении
божественное триединство: малый отрезок
олицетворял Сына, большой – Отца, а
целое – Святой дух.

8. Создатель чисел Фиббоначи

Леона́рдо Пиза́нский (около 1170 года— около
1250 года) — первый крупный математик
средневековой Европы. Наиболее известен под
прозвищем Фибона́ччи.
Непосредственным образом с
правилом золотого сечения
связано имя итальянского
математика
Леонардо Фибоначчи.

9. Создатель чисел Фиббоначи

В результате решения одной из задач ученый
вышел на последовательность чисел, известную
сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34,
55 и т.д. На отношение этой последовательности к
золотой пропорции обратил внимание Кеплер:
«Устроена она так, что два младших члена этой
нескончаемой пропорции в сумме дают третий
член, а любые два последних члена, если их
сложить, дают следующий член, причем та же
пропорция сохраняется до бесконечности».
Сейчас ряд Фибоначчи это арифметическая
основа для расчетов пропорций золотого сечения
во всех его проявлениях.

10.

Эту последовательность можно
изобразить графически, в виде так
называемой спирали Фибоначчи. Эта
спираль почти идентична логарифмической
спирали фи, известной как спираль
золотого сечения. Разница заключается в
том, что спираль Фибоначчи – это
интерпретация (при помощи целых чисел)
арифметически невозможной спирали
золотого сечения, у которой нет ни конца,
ни начала. У спирали Фибоначчи есть
определенное начало.

11. Золотая спираль Структура «Золотой спирали» символизирует две хорошо известные в сакральной геометрии фигуры: спираль Золотого

Золотая спираль
Структура «Золотой
спирали» символизирует две хорошо
известные в сакральной геометрии
фигуры: спираль Золотого сечения(фи)
и спираль Фибоначчи.

12.

Фи – это постоянное число, влияние которого
даже более глубоко и загадочно, чем Пи. Знаки
после запятой просто продолжаются до
бесконечности, не повторяясь. Особенность этого
числа в том, что его можно найти во всех известных
органических структурах. Пропорция фи есть везде,
от строения костей человека до спирального
расположения семян подсолнуха и завитков раковин
моллюсков. Она лежит в основе всех биологических
структур и кажется геометрической схемой самой
жизни.
Платон называл пропорцию фи «ключом к физике
космоса». Число фи – 1,6180339+.

13. Золотая спираль в природе

14. Золотая спираль в природе

15. Золотая спираль в природе

16. Золотая спираль в живописи

17. Золотая спираль в теле человека

18. Золотая спираль в теле человека

19. Золотое сечение в архитектуре

20. Золотая спираль в архитектуре

21. Золотое сечение в скульптурах

Пропорции человеческого тела использовались
еще античными мастерами при создании
скульптур. Известна золотая пропорция статуи
Аполлона Бельведерского: рост изображенного
человека делится пупочной линией в золотом
сечении. Иногда эту статую так и называли «Канон Поликлета», вслед за одноименным
теоретическим трактатом его создателя. Поликлет
выводил там цифровой закон идеальных
пропорциях человека. Эти пропорции находятся
друг с другом в цифровом соотношении.

22. Золотое сечение в скульптурах

• Дорифор — это не изображение конкретного
спортсмена-победителя, а иллюстрация канонов
мужской фигуры.
• Венера Милосская, статуя богини Афродиты и
эталон женской красоты, является одним из
лучших памятников греческого скульптурного
искусства - также построена на пропорциях
золотого сечения.

23. Золотая спираль в архитектуре нашего города

24. Золотая спираль в архитектуре нашего города

25. Золотая спираль в архитектуре нашего города

26. Рукотворная золотая спираль из природных материалов

27. Исследования

• Так как у нас работа связана с золотым
сечением, мы решили сделать немного
экспериментов. Мы измерили наших
одноклассников: возьмем рост буквой
(a), расстояние от талии до пола
буквой(b), расстояние от талии до
макушки буквой(c)
• Мы нашли отношения A:B, B:С
• Как известно золотое сечение
составляет 1.618…

28. Результат исследования

• у 36% в отношении присутствует 1,61-1,62
• у 50% отношение равно 1,55-1,67
• Самые пропорциональные телосложения
оказались у 3 учеников (21%)

29. Опрос

• Так же мы решили сделать небольшой
опрос в нашем классе.
• Мы напечатали на листах А4 пять
прямоугольников один прямоугольник
мы сделали под размеры золотого
сечения, а остальные мы сделали
просто обычными.

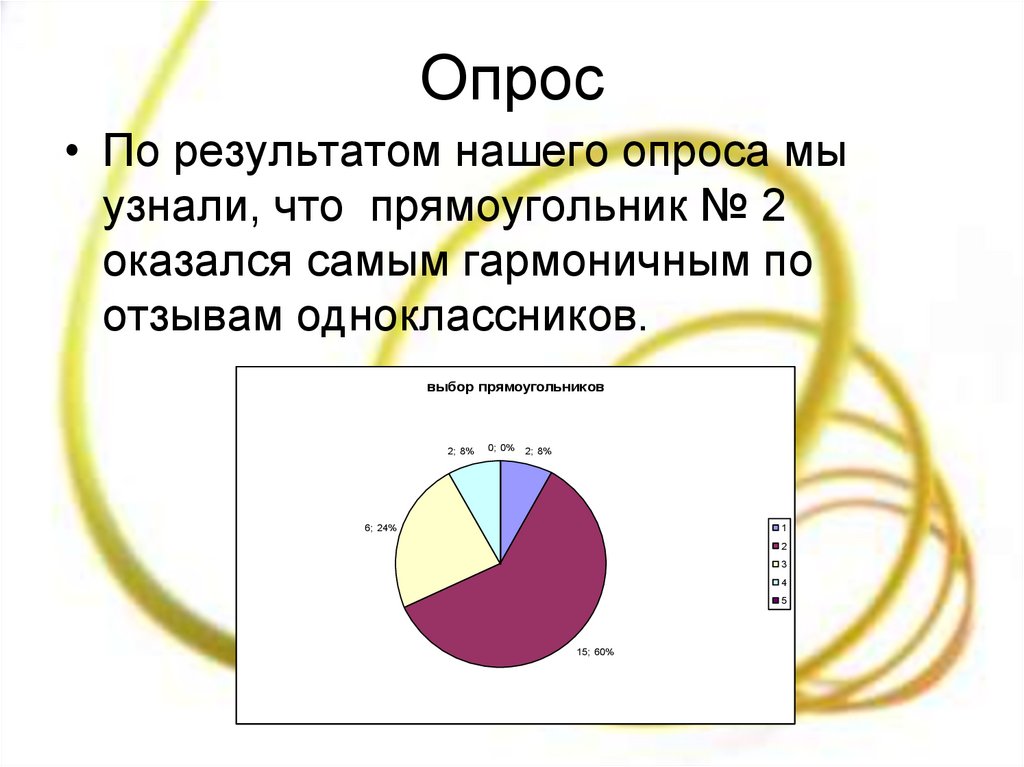
30. Опрос

• По результатом нашего опроса мы
узнали, что прямоугольник № 2
оказался самым гармоничным по
отзывам одноклассников.
выбор прямоугольников
2; 8%
0; 0%
2; 8%
6; 24%
1
2
3
4
5
15; 60%

31. Заключение

• В ходе работы мы узнали, что золотое
сечение присутствует: в природе, в
теле человека, в архитектуре.
Мы исследовали предметы
окружающие нас и пропорции своего
тела и обнаружили сами Золотую
пропорцию в окружающем нас мире.

32. Вывод

• Золотое сечение - это один из основных
принципов природы.
• Человеческое представление о
красивом сформировалось под
влиянием того - какую гармонию и
порядок видит он сам в природе.
• Закономерности золотого сечения
используются в архитектуре
строителями и архитекторами.

33. Вывод

• Золотое сечение есть и будет всегда
отображаться в окружающем мире.
• Установлено, что золотые отношения
можно найти и в пропорциях
человеческого тела. Кроме того,
человек сам является творцом, создаёт
замечательные произведения
искусства, в которых просматривается
золотая пропорция.