Similar presentations:
Задачи на части
1.
.2.
• «Главнаясила
математики
состоит в том, что вместе с
решением одной конкретной задачи
она создаёт общие приёмы и
способы, применимые во многих
ситуациях , которые даже не всегда
можно предвидеть»
М. И. Башмаков
3.
• Мальчик и девочка рвали в лесу орехи.• Всего они сорвали 120 штук. Девочка
сорвала в два раза меньше мальчика.
• Сколько орехов было у мальчика и
девочки в отдельности?
4.
Тема урока:5.
Задачи на частиПодумайте и ответьте: какое важное условие
(которое не оговаривается, но
принимается по умолчанию) должно
выполняться в задачах на части ?
Подсказка: это хорошо видно на схеме.
ПОДУМАЙ!
Все части, о которых идет речь в задаче,
равные.
6.
Подумайте и ответьте: что первымделом необходимо найти при решении
задачи на части?
ПОДУМАЙ!
Нужно узнать, сколько составляет одна
часть.
7.
Задача №1В первой пачке 60
тетрадей, а во
второй - в 2 раза
больше. Сколько
всего тетрадей?
Задача №2
В двух пачках 60
тетрадей. Во второй
пачке тетрадей в 2
раза меньше, чем в
первой. Сколько
тетрадей в каждой
пачке?
8.
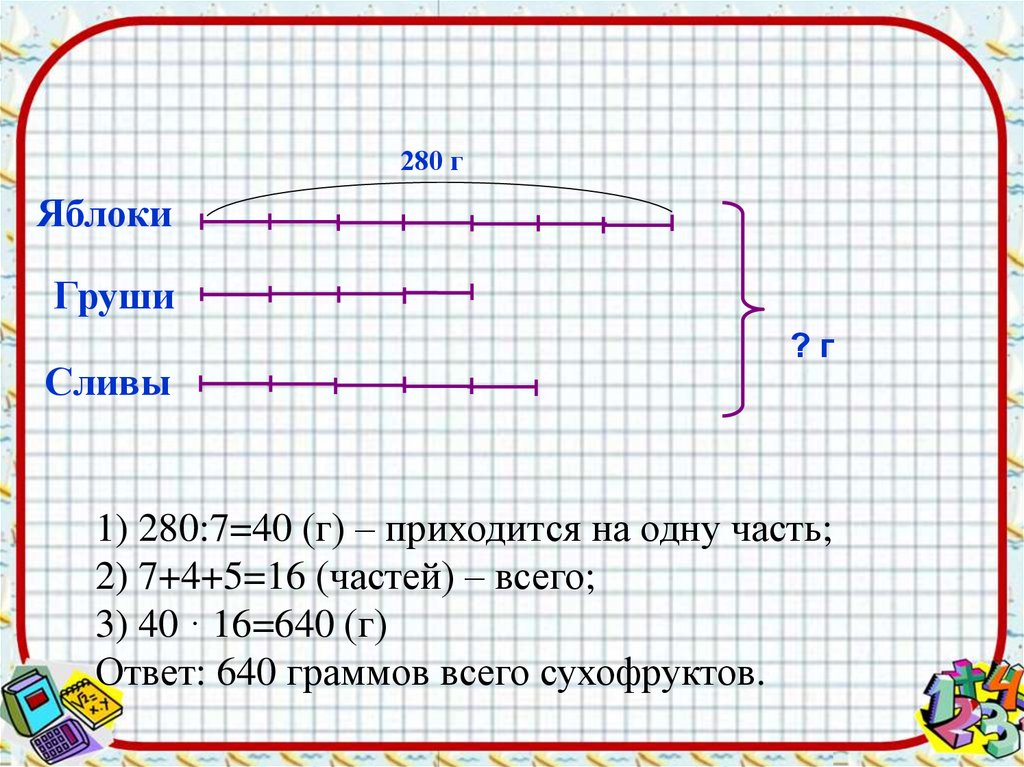
• Для компота взяли сухофрукты: 7частей яблок, 4 части груш и 5 частей
слив. Известно, что яблок взяли 280
грамм. Сколько граммов сухофруктов
всего взяли для компота?
9.
280 гЯблоки
Груши
Сливы
?г
1) 280:7=40 (г) – приходится на одну часть;
2) 7+4+5=16 (частей) – всего;
3) 40 · 16=640 (г)
Ответ: 640 граммов всего сухофруктов.
10.
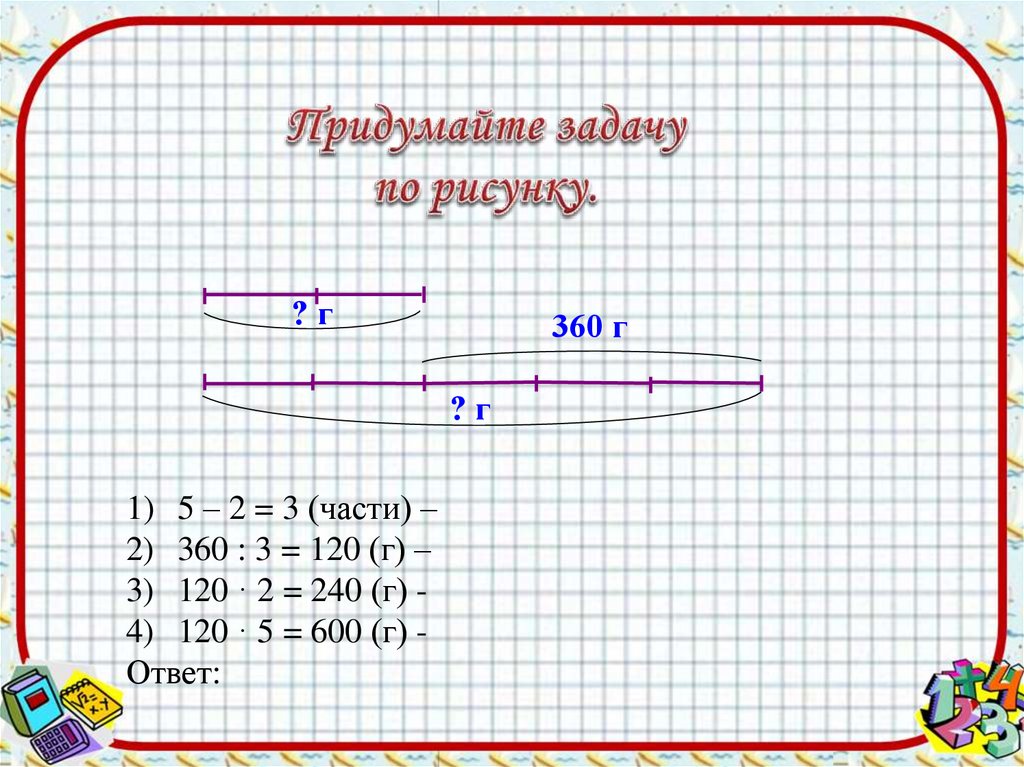
?г360 г
?г
1) 5 – 2 = 3 (части) –
2) 360 : 3 = 120 (г) –
3) 120 · 2 = 240 (г) 4) 120 · 5 = 600 (г) Ответ:
11.
1.2.
1
2
3
В
А
Б
1) 4 + 3 + 2 = 9 (частей) – всего приходится на 1800 г;
2) 1800 : 9 = 200 ( г ) – приходится на 1 часть;
3) 200 · 4 = 800 ( г ) – купили яблок;
4) 200 · 3 = 600 ( г ) – купили груш;
5) 200 · 2 = 400 ( г ) – купили слив
Ответ: 800 граммов яблок, 600 граммов груш, 400 граммов
слив.










 mathematics
mathematics








