Газовые законы (изопроцессы)

1. Газовые законы (ИЗОПРОЦЕССЫ)

2. Изопроцесс - процесс изменения состояния идеального газа при неизменном значении одного из макроскопических параметров (р, V,

Т).

3. PV = nRT

PV = nRT
Если масса газа и его молярная масса
фиксированы, то состояние газа
определяется тремя макроскопическими
параметрами:
1. давлением,
2. объёмом,
3. температурой.
Эти параметры связаны друг с другом
уравнением состояния (уравнением
Менделеева — Клапейрона).

4. или

n – число молей газа число молей газа
;
P – давление газа, Па;
M- молярная масса газа;
V – объем газа, м3;
m- масса газа;
T – абсолютная температура газа, К;
R – универсальная газовая постоянная 8,314 Дж/моль×K.
Если объём газа выражен в литрах, то уравнение КлапейронаМенделеева записывается в виде:

5. Из уравнения Клапейрона-Менделеева следует три закона:

Из уравнения КлапейронаМенделеева следует три
закона:
1.
Закон Шарля:
2. Закон Гей-Люссака:
3. Закон Болйя-Мариотта:

6.

Термодинамический процесс (или просто процесс) —
это изменение состояния газа с течением времени. В
ходе термодинамического процесса меняются значения
макроскопических параметров — давления, объёма и
температуры.
Особый интерес представляют изопроцессы —
термодинамические процессы, в которых значение
одного из макроскопических параметров остаётся
неизменным. Поочерёдно фиксируя каждый из трёх
параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной
температуре газа: T = const.
2. Изобарный процесс идёт при постоянном давлении
газа: p = const.
3. Изохорный процесс идёт при постоянном объёме
газа: V = const.

7.

• Графики термодинамических
процессов принято изображать в
следующих системах координат:
• pV-диаграмма: ось абсцисс V ,
ось ординат p;
• V T-диаграмма: ось абсцисс T,
ось ординат V ;
• pT-диаграмма: ось абсцисс T, ось
ординат p.

8. ИЗОТЕРМИЧЕСКИЙ процесс -

ИЗОТЕРМИЧЕСКИЙ процесс процесс изменения состояния
идеального газа при
постоянной температуре.
Поршень
легко
подвижен
V↓ → р↑
p↓ → V↑

9. Изотермический процесс

• Пусть идеальный газ совершает изотермический
процесс при температуре T. В ходе процесса
меняются только давление газа и его объём.
• Рассмотрим два произвольных состояния газа: в одном
из них значения макроскопических параметров равны
p1; V1; T, а во втором — p2; V2; T.
• Эти значения связаны уравнением МенделееваКлапейрона: p1V1 =(m/u)RT; p2V2 =(m/u)RT
• Как мы сказали с самого начала, масса m и молярная
масса предполагаются неизменными.
• Поэтому правые части выписанных уравнений равны.
Следовательно, равны и левые части:
• p1V1 = p2V2:

10. К этому выводу пришёл английский учёный Роберт Бойль в 1960 г и французский физик, физиолог и священник Эдм Мариотт.

11. Закон Бойля -Мариотта

Произведение давления газа
данной массы на его объём
постоянно, если его
температура не меняется.
T=const
рV=conct

12. Графики изотермического процесса

• График изотермического процесса
называется изотермой.
• Изотерма на pV-диаграмме — это
график обратно пропорциональной
зависимости p = constV.
• Такой график является гиперболой
(вспомните алгебру —график
функции у= k/х ).

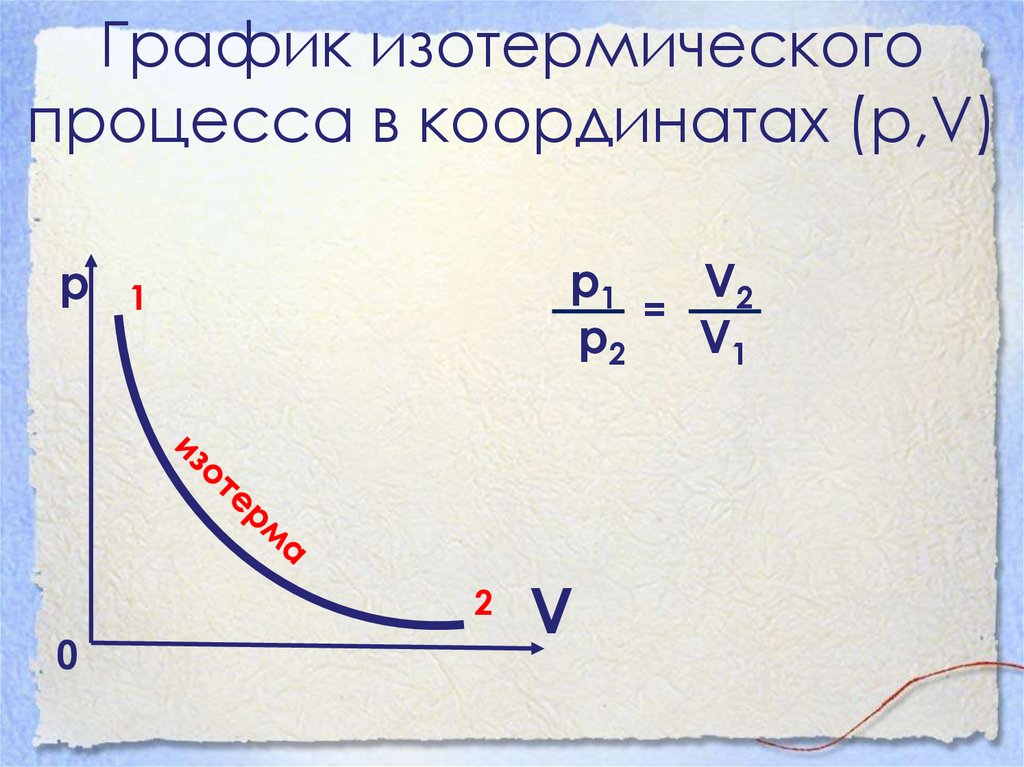
13. График изотермического процесса в координатах (р,V)

р
р1
V2
=
р2
V1
1
2
0
V

14.

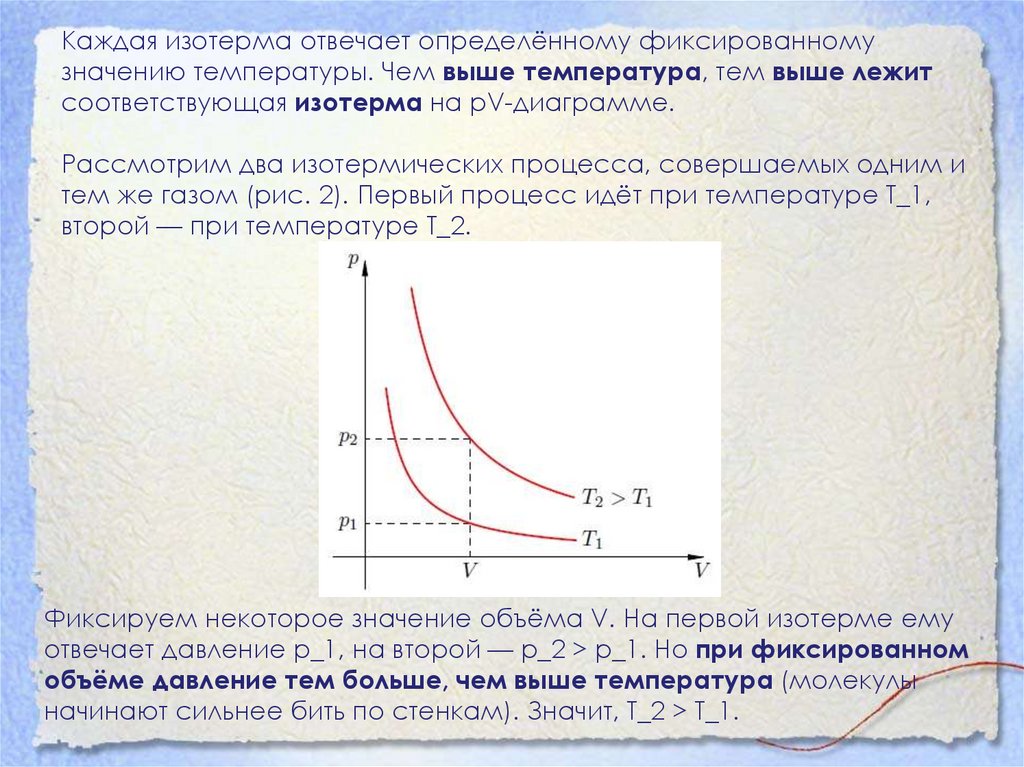
Каждая изотерма отвечает определённому фиксированному
значению температуры. Чем выше температура, тем выше лежит
соответствующая изотерма на pV-диаграмме.
Рассмотрим два изотермических процесса, совершаемых одним и
тем же газом (рис. 2). Первый процесс идёт при температуре T_1,
второй — при температуре T_2.
Фиксируем некоторое значение объёма V. На первой изотерме ему
отвечает давление p_1, на второй — p_2 > p_1. Но при фиксированном
объёме давление тем больше, чем выше температура (молекулы
начинают сильнее бить по стенкам). Значит, T_2 > T_1.

15. График изотермического процесса в координатах(р,Т)

изотерма
р
0
Т

16.

График изотермического
процесса в координатах(V,Т)
изотерма
V
0
Т

17. ИЗОБАРНЫЙ процесс -

ИЗОБАРНЫЙ процесс процесс изменения
состояния идеального
газа при постоянном
давлении.
Поршень
легко
подвижен
T↓ → V↓
T↑ → V↑

18. Этот закон экспериментально был открыт в 1802г. французским учёным Жозефом Луи Гей-Люссаком

19.

Типичный пример изобарного процесса:
газ находится под массивным поршнем,
который может свободно перемещаться.
Если масса поршня M и поперечное
сечение поршня S, то давление газа всё
время постоянно и равно p=p0+MgS;
где p0 — атмосферное давление.

20.

• Пусть идеальный газ совершает изобарный процесс при
давлении p. Рассмотрим два произвольных состояния газа; на
этот раз значения макроскопических параметров будут равны
p; V1; T1 и p; V2; T2.
• Выпишем уравнения состояния: pV1 =mRT1; pV2 =mRT2:
• Поделив их друг на друга, получим: V1/V2=T1/T2:
• Перепишем полученное соотношение так, чтобы в одной части
фигурировали только параметры первого состояния, а в
другой части — только параметры второго состояния
V1/T1=V2/T2
• А отсюда теперь — ввиду произвольности выбора состояний! —
получаем закон Гей-Люссака: V/T= const
• При постоянном давлении газа его объём прямо
пропорционален температуре : V = constT
• Почему объём растёт с ростом температуры? При
повышении температуры молекулы начинают бить сильнее и
приподнимают поршень. При этом концентрация молекул
падает, удары становятся реже, так что в итоге давление
сохраняет прежнее значение.

21. Закон Гей-Люссака:

Относительное изменение
объёма газа данной массы при
постоянном давлении прямо
пропорционально изменению
температуры.
V
р = const
= const
Т
При постоянном давлении газа его объём
прямо пропорционален температуре:
V = const · T.

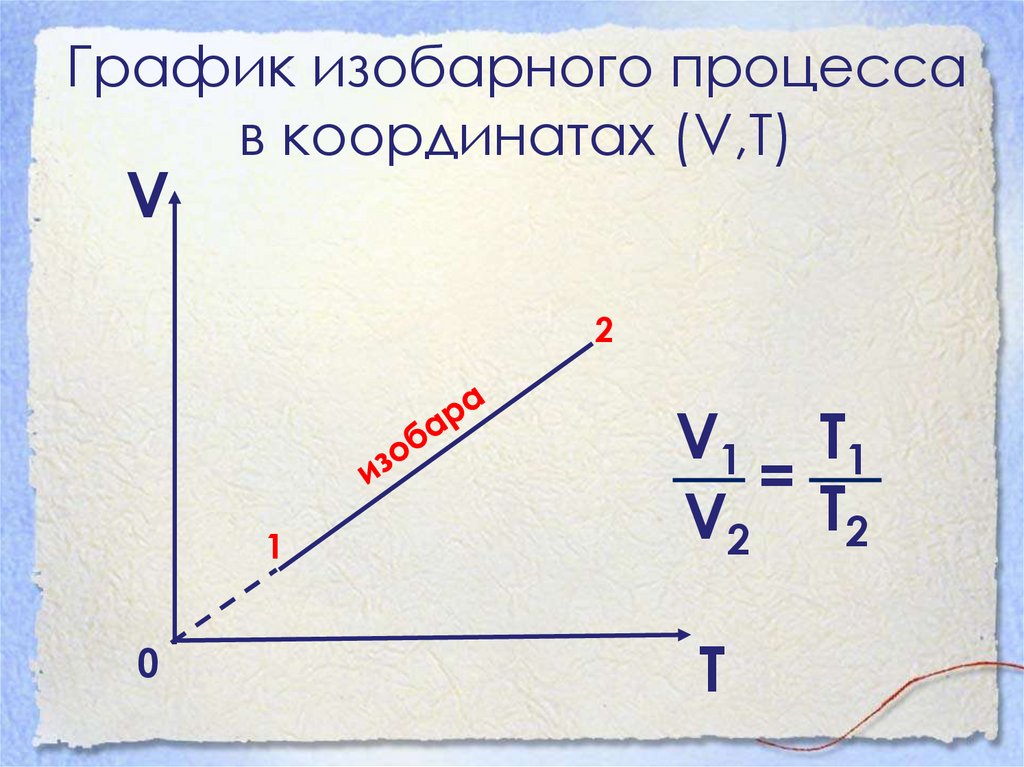
22. График изобарного процесса в координатах (V,Т)

V
2
1
0
V1 Т1
=
V2 Т2
T

23.

• Пунктирный участок графика означает, что в
случае реального газа при достаточно низких
температурах модель идеального газа (а вместе
с ней и закон Гей-Люссака) перестаёт работать.
В самом деле, при снижении температуры
частицы газа двигаются всё медленнее, и силы
межмолекулярного взаимодействия оказывают
всё более существенное влияние на их движение
(аналогия: медленный мяч легче поймать, чем
быстрый).
• При совсем низких температурах газы и вовсе
превращаются в жидкости.

24. Как меняется положение изобары при изменении давления?

• Чем больше давление, тем ниже идёт изобара на VTдиаграмме.
• Рассмотрим две изобары с давлениями p_1 и p_2
Зафиксируем некоторое значение температуры T.
Мы видим, что V_2 < V_1. Но при фиксированной температуре объём
тем меньше, чем больше давление (закон Бойля — Мариотта!).
Значит, p_2 > p_1.

25.

График изобарного процесса
в координатах (р,Т)
р
изобара
0
T

26.

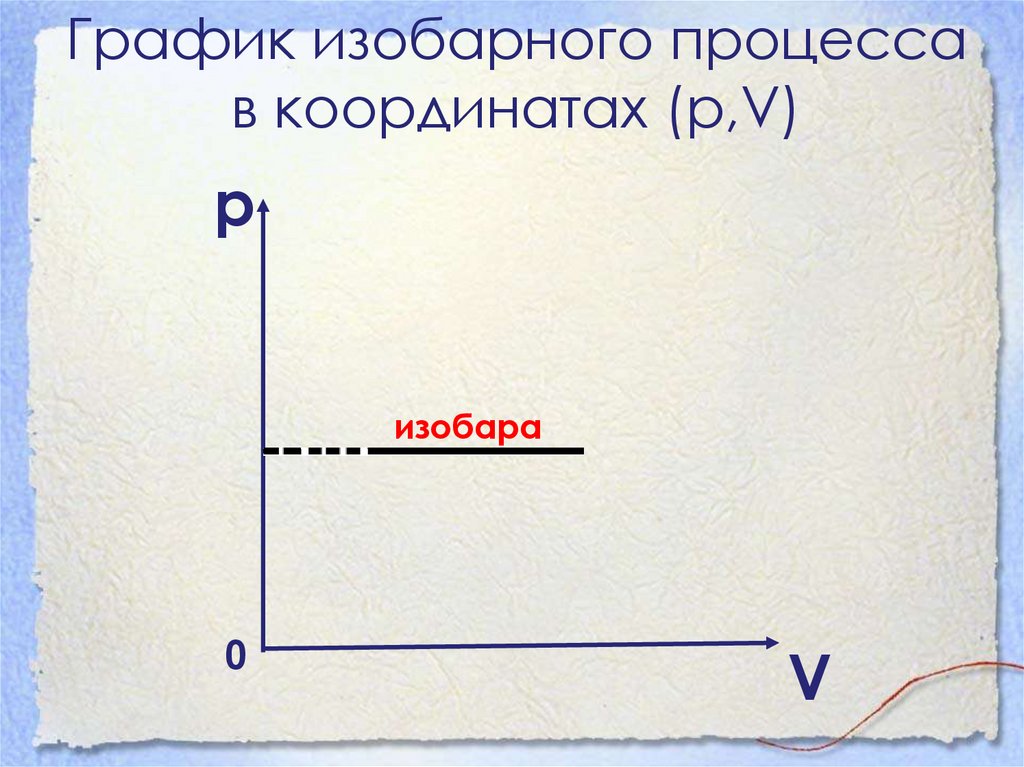
График изобарного процесса
в координатах (р,V)
р
изобара
0
V

27. Изохорный процесс

Изохорный процесс (от греческого слова
«хорема»-вместимость)— это процесс, проходящий
при постоянном объёме. При изохорном процессе
меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто:
это процесс, идущий в жёстком сосуде
фиксированного объёма (или в цилиндре под
поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс
в сосуде объёмом V . Опять-таки рассмотрим два
произвольных состояния газа с параметрами p1; V;
T1 и p2; V; T2.
Имеем: p1V =mRT1; p2V =mRT2

28.

• Делим эти уравнения друг на друга:
P1/p2=T1/T2
• Как и при выводе закона Гей-Люссака,
«разносим» индексы в разные части:
P1/T1=P2/T2
• Ввиду произвольности выбора состояний мы
приходим к закону Шарля: p/T= const
• Иными словами, при постоянном объёме
газа его давление прямо пропорционально
температуре:
p = const T
• Увеличение давления газа фиксированного
объёма при его нагревании — вещь совершенно
очевидная с физической точки зрения.

29. ИЗОХОРНЫЙ процесс -

ИЗОХОРНЫЙ процесс процесс изменения
состояния идеального
газа при постоянном
объёме.
Поршень закреплен
T↓ → р↓
T↑ → p↑

30. Эту зависимость экспериментально установил в 1787 г.французский физик Жак Шарль.

31. Закон Шарля:

Давление данной массы газа
при постоянном объёме прямо
пропорционально абсолютной
температуре.
V = const
р
= cоnst
Т

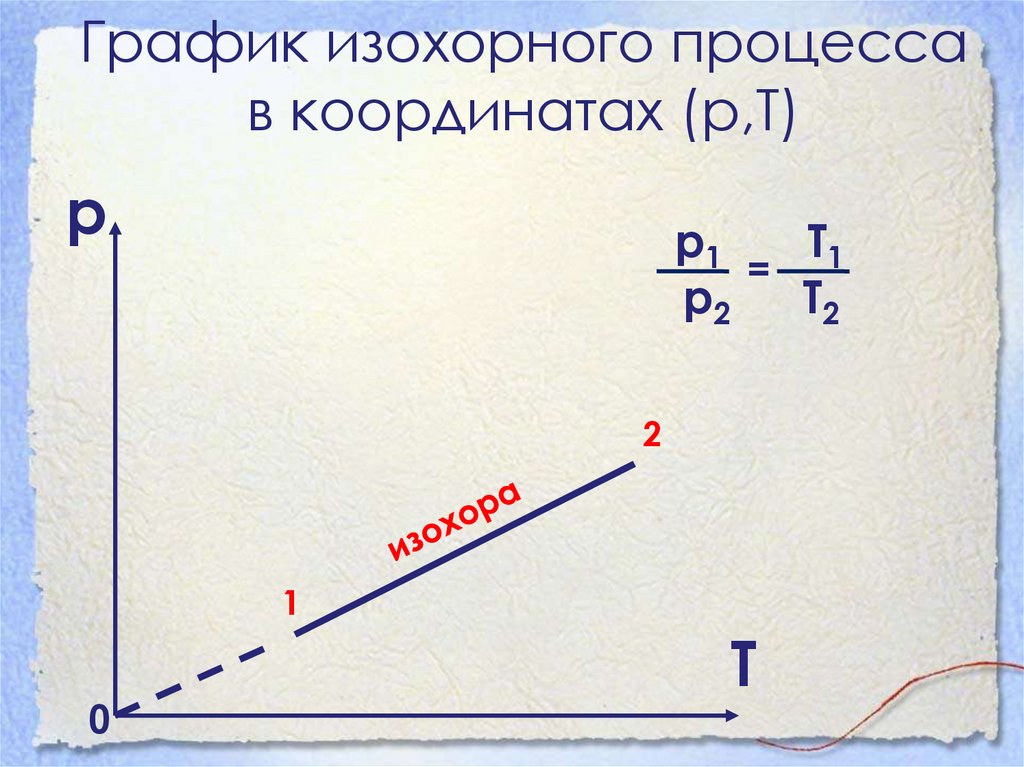
32. График изохорного процесса в координатах (р,Т)

р
р1
Т1
=
р2
Т2
2
1
0
Т

33.

График изохорного процесса
в координатах (V,Т)
V
изохора
0
Т

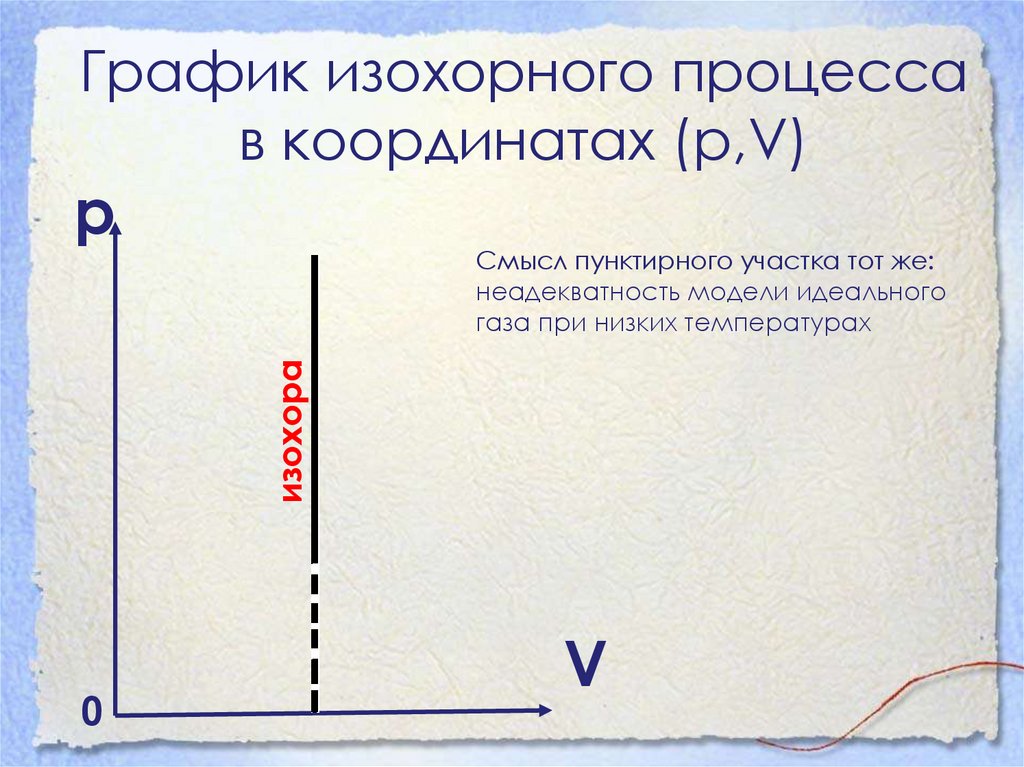
34.

График изохорного процесса
в координатах (р,V)
р
изохора
Смысл пунктирного участка тот же:
неадекватность модели идеального
газа при низких температурах
0
V

35. Эти законы справедливы для любых газов, а так же для смесей газов(например, воздуха).

Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также
газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона.
Но исторически всё было наоборот: газовые законы были установлены
экспериментально, и намного раньше. Уравнение состояния
появилось впоследствии как их обобщение.

36.

Другие виды процессов в
идеальном газе
Адиабатический процесс
(изоэнтропийный). Термодинамический
процесс, происходящий без
теплообмена с окружающей средой.
Политропический процесс. Процесс,
при котором теплоёмкость газа
остаётся постоянной. Политропический
процесс – общий случай всех
перечисленных выше процессов.

37.

Другие газовые законы.
Закон Авогадро: При одинаковых давлениях и одинаковых
температурах, в равных объёмах различных идеальных газов
содержится одинаковое число молекул. В одном моле
различных веществ содержится NA=6,02·1023молекул (число
Авогадро).
Моль любого вещества в газообразном состоянии при
одинаковых температурах и давлениях занимает один и тот же
объем. Как показали эксперименты, при нормальных условиях
(р=1 атм(760 мм.рт.ст.), T=273K(Т=О С)) он равен 22,414 л.
Закон Дальтона. Давление смеси идеальных газов равно сумме
парциальных давлений Р, входящих в неё газов:
Парциальное давление Pn – давление, которое оказывал бы
данный газ, если бы он один занимал весь объем.
Для смеси двух газов:

38.

Подписать графики
p
Подписать графики
p
V
0
V
Подписать графики
0
T
0
T
ИЗОТЕРМА
ИЗОТЕРМА
ИЗОТЕРМА
ИЗОБАРА
ИЗОБАРА
ИЗОБАРА
ИЗОХОРА
ИЗОХОРА
ИЗОХОРА

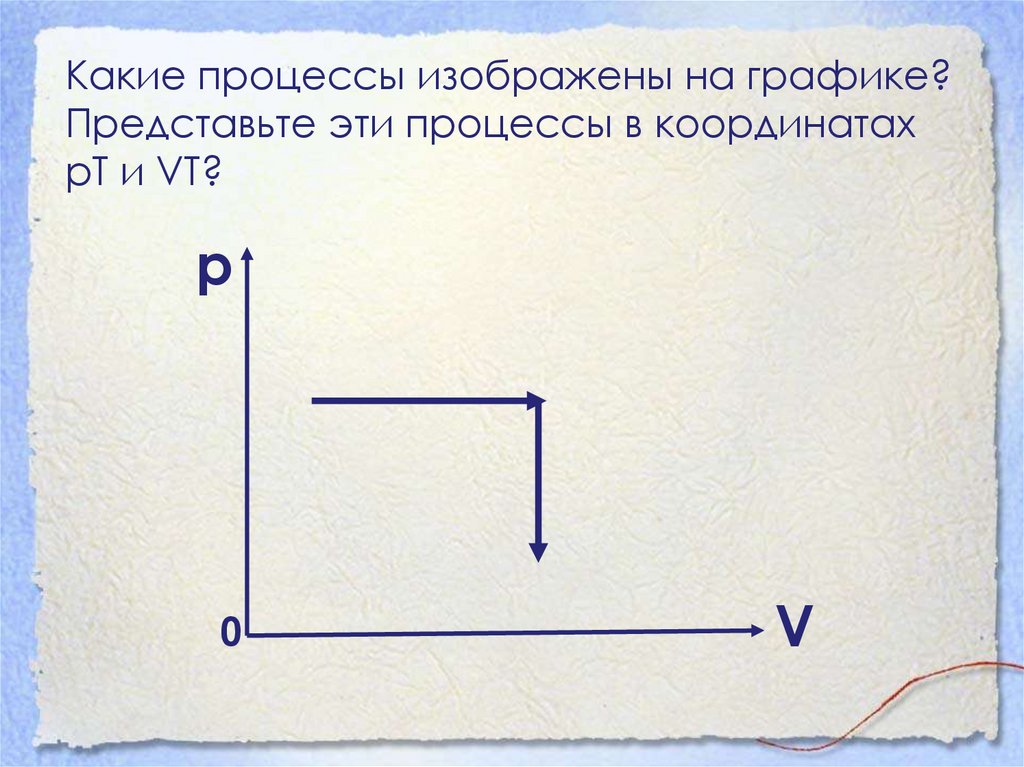
39. Какие процессы изображены на графике? Представьте эти процессы в координатах рТ и VT?

р
0
V

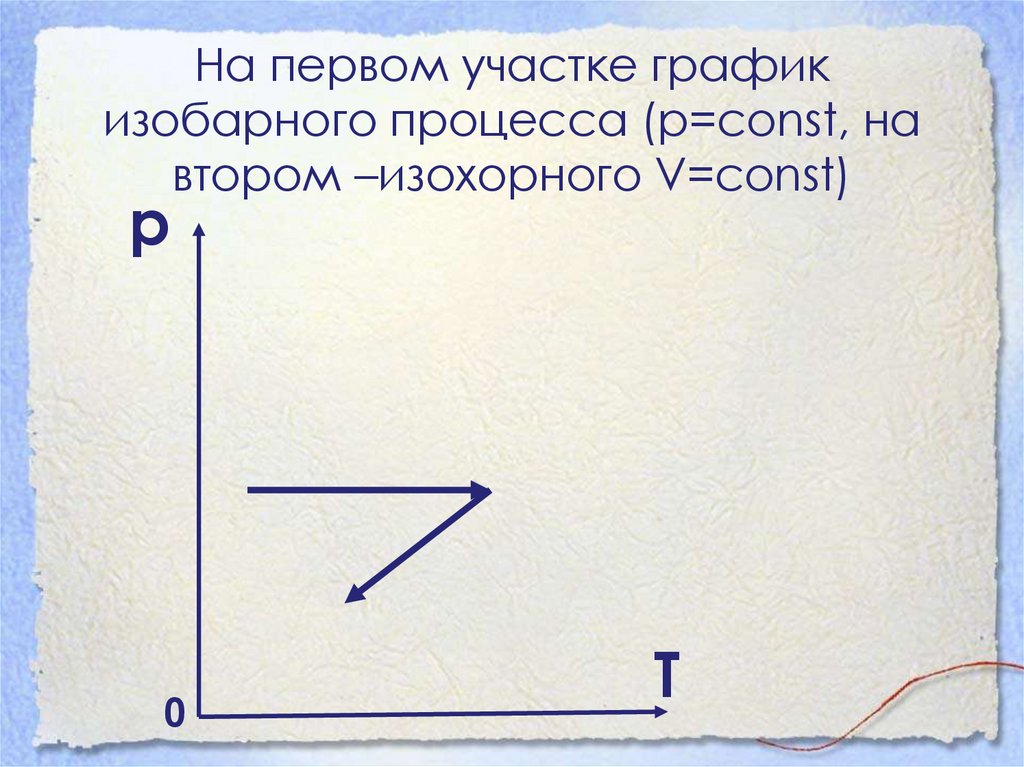
40. На первом участке график изобарного процесса (р=const, на втором –изохорного V=const)

р
0
Т

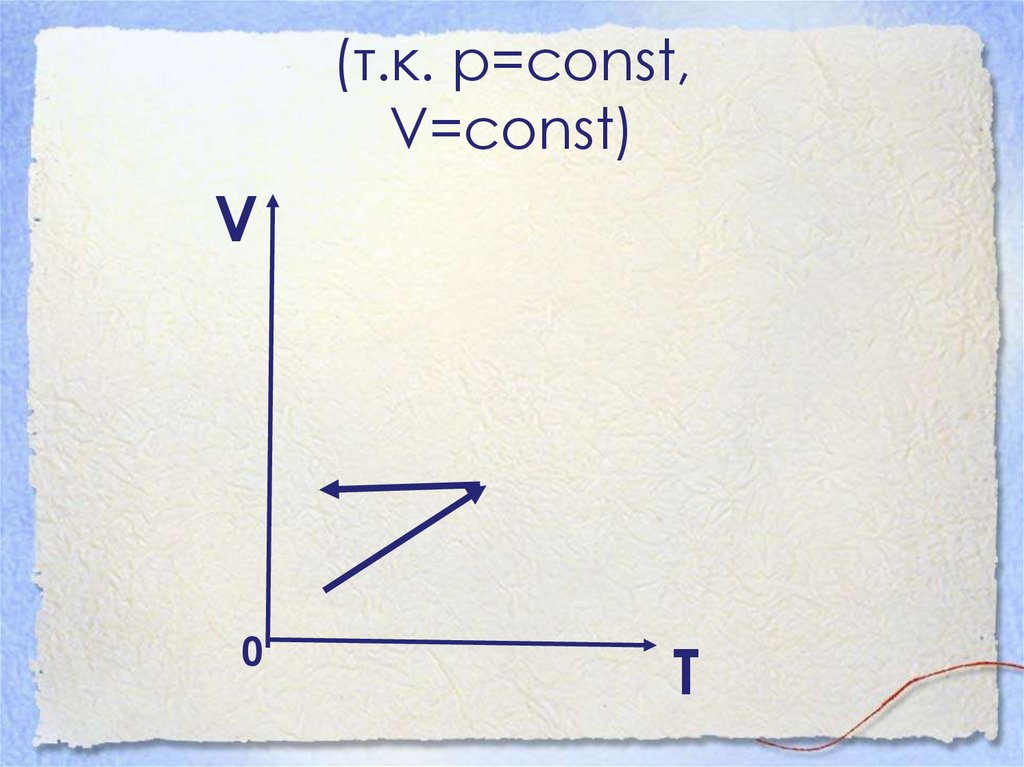
41. (т.к. р=const, V=const)

V
0
T

42.

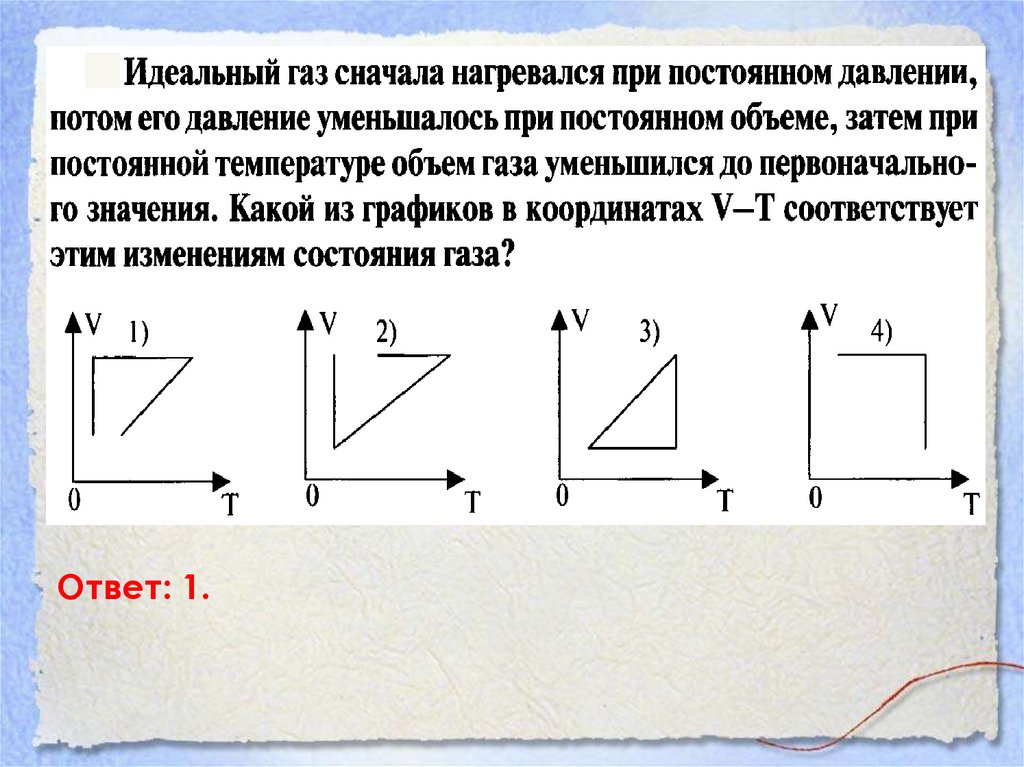
Ответ: 1.

43.

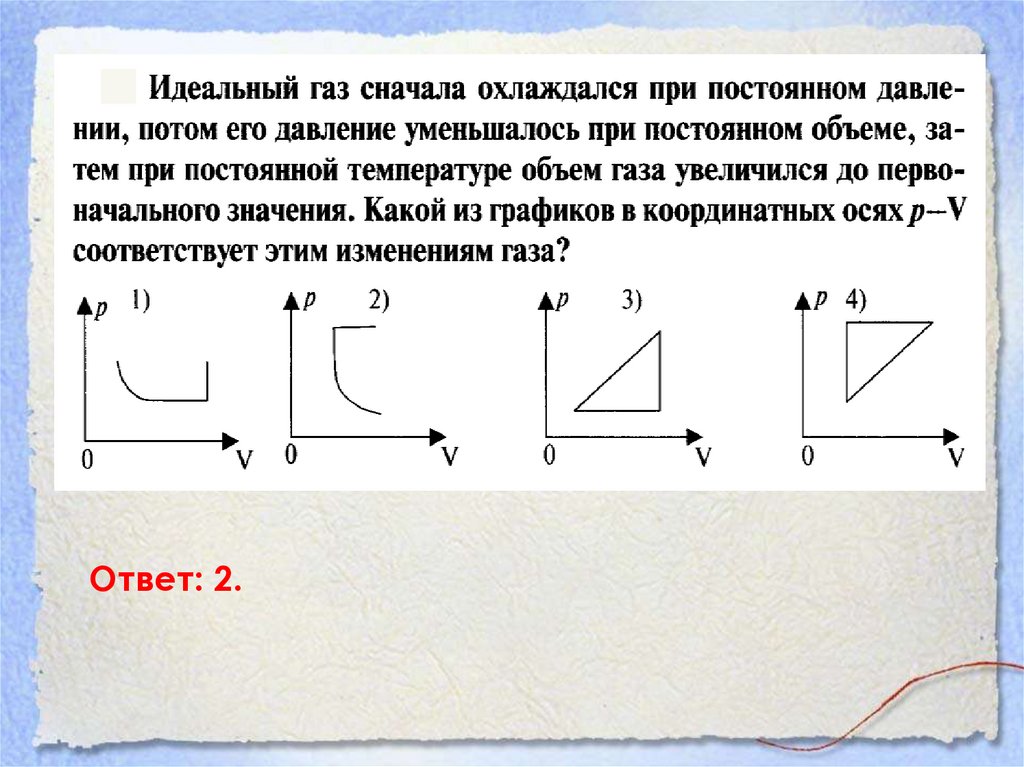
Ответ: 2.

44.

Задание.
По графику изменения
состояния идеального газа в
координатах (p,T) изобразить
изменение его состояния в
координатах (p,V) и (V,T)
Решение.

45.

Обратите внимание
1.
Если по условию параметры состояния газа не
изменяются, запишите уравнение МенделееваКлапейрона и выразите неизвестную величину
Если по условию даны два или несколько состояний
газа, то при решении задач рекомендуется
соблюдать последовательность:
Параметры состояния газа (как данные, так и
искомые) запишите по форме:
1
состояние
газа
m1=…
p1=…
V1=…
T1=…
2
состояние
газа
m2=…
p2=…
V2=…
T2=…
2.
Запишите уравнение Менделеева-Клапейрона для
каждого состояния, дополнительные условия, решите
систему уравнений относительно искомой величины.

46.

Пр.1
В цилиндре под
поршнем находится
воздух. Вес поршня
Р=60 Н, площадь
цилиндра S0=20см2,
атмосферное
давление р0=105 Па.
Груз какого веса надо
положить на поршень,
чтобы объем воздуха в
цилиндре уменьшился в
два раза? Трение не
учитывайте,
температура
постоянна?
P0
?
Р
?
S0
ПУСК

47.

Пр.1
В цилиндре под поршнем находится воздух. Вес
поршня Р=60 Н, площадь цилиндра S0=20см2,
атмосферное давление р0=105 Па. Груз какого веса
надо положить на поршень, чтобы объем воздуха в
цилиндре уменьшился в два раза? Трение не
учитывайте, температура постоянна?
1 состояние газа
m1=m p1=p0+(P/S0)
2 состояние газа
m2=m p2=p0+(P/S0)+(P1/S0) V2=V1/2 T2=T
P1-?
V1
T1=T

48.

Пр.1
1 состояние газа
m1=m p1=p0+(P/S0)
2 состояние газа
m2=m p2=p0+(P/S0)+(P1/S0) V2=V1/2 T2=T
P1-?
V1
T1=T
Решение:
P/S0-давление поршня; P1/S0-давление груза.
Согласно закону Бойля-Мариотта p1V1=p2V2;
(p0+P/S0)V1=(p0+P/S0+P1/S0)(V1/2).
Отсюда
P1=p0S0+P=260(Н).
Ответ: P1=260Н.

49.

Пр.2
Объем пузырька газа, всплывшего со дна
озера на поверхность, увеличился в три раза.
Какова глубина озера?
1
m1=
p 1=
V1=
T1=
m2=
p2=
V2=
T2=
2
h-?
m
3m m/3
m/3
pa
p0
pж
ж
V
+
-
*
3V V/3 3/V
T
3/T T/3

50.

Пр.2
В связи с тем, что масса
газа и его температура не
изменяются, воспользуемся
уравнением
изотермического процесса
p1V1=p2V2
(pа+
p1 – давление
на глубине h;
p2 – давление на
поверхности озера.
в gh)V=pа*3V.
pа
Выразите h и подставьте
значения.
h
Проверьте результат:
Ответ: h=20м.
К содержанию
pж
ПУСК

51.

№1
Как изменится давление идеального
газа при увеличении температуры и
объема газа в 4 раза?
ПУСК
Далее

52.

№2
В одинаковых сосудах при одинаковой
температуре находятся водород (Н2) и
углекислый газ (СО2). Массы газов
одинаковы. Какой из газов и во сколько раз
оказывает большее давление на стенки
сосуда?
m(H2) =
Далее
m(CO2)

53.

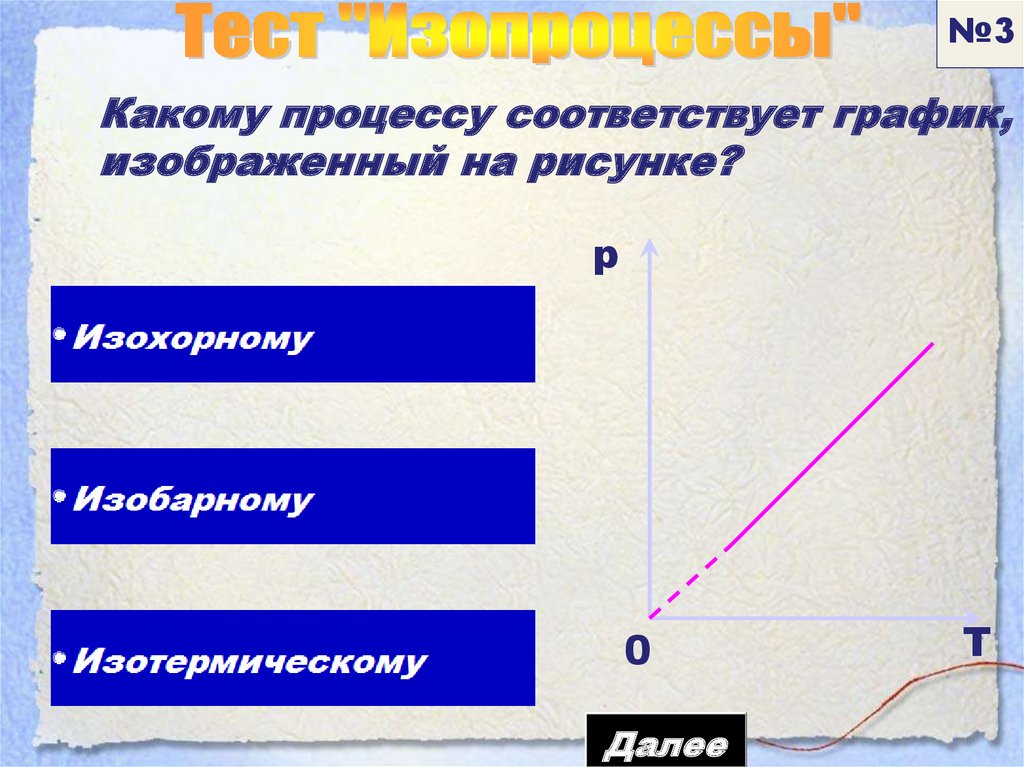
№3
Какому процессу соответствует график,
изображенный на рисунке?
p
0
Далее
Т

54.

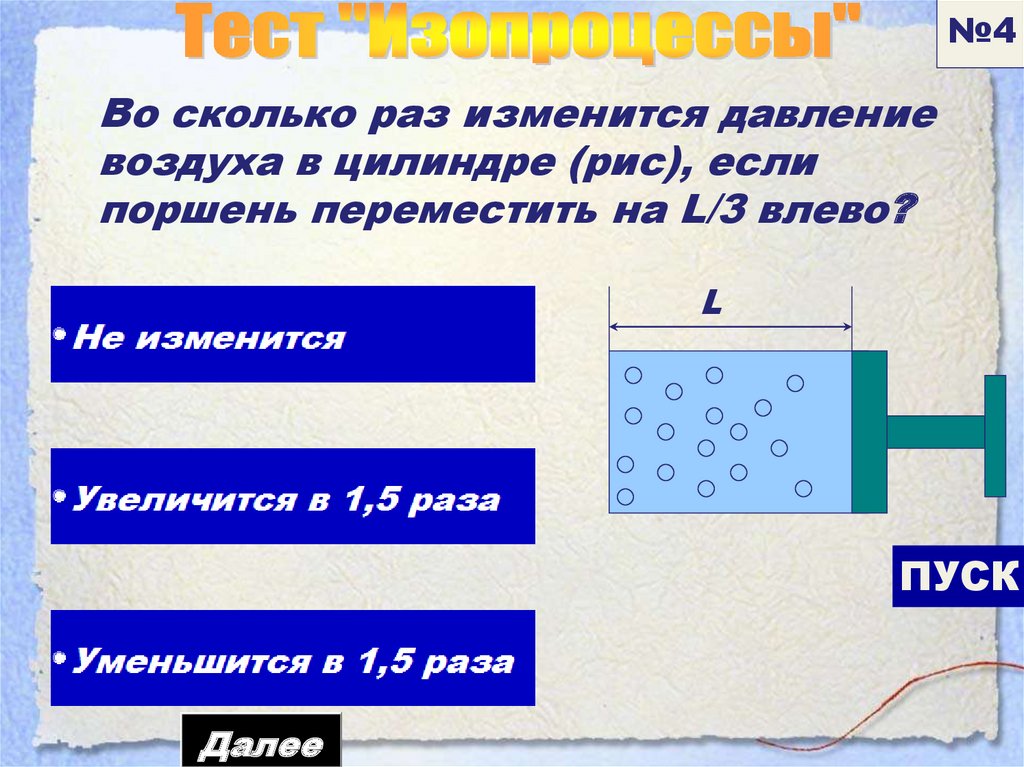
№4
Во сколько раз изменится давление
воздуха в цилиндре (рис), если
поршень переместить на L/3 влево?
L
ПУСК
Далее

55.

№5
Во сколько раз отличается плотность
метана (СР4) от плотности кислорода
(О2) при одинаковых условиях?
?
Далее