Метод консалтинга при проведении внеклассного занятия

1.

Полякова М. Н.
МБОУ «Средняя общеобразовательная школа с углубленным изучением
отдельных предметов №14», г. Иркутск
МЕТОД КОНСАЛТИНГА ПРИ
ПРОВЕДЕНИИ ВНЕКЛАССНОГО ЗАНЯТИЯ

2.

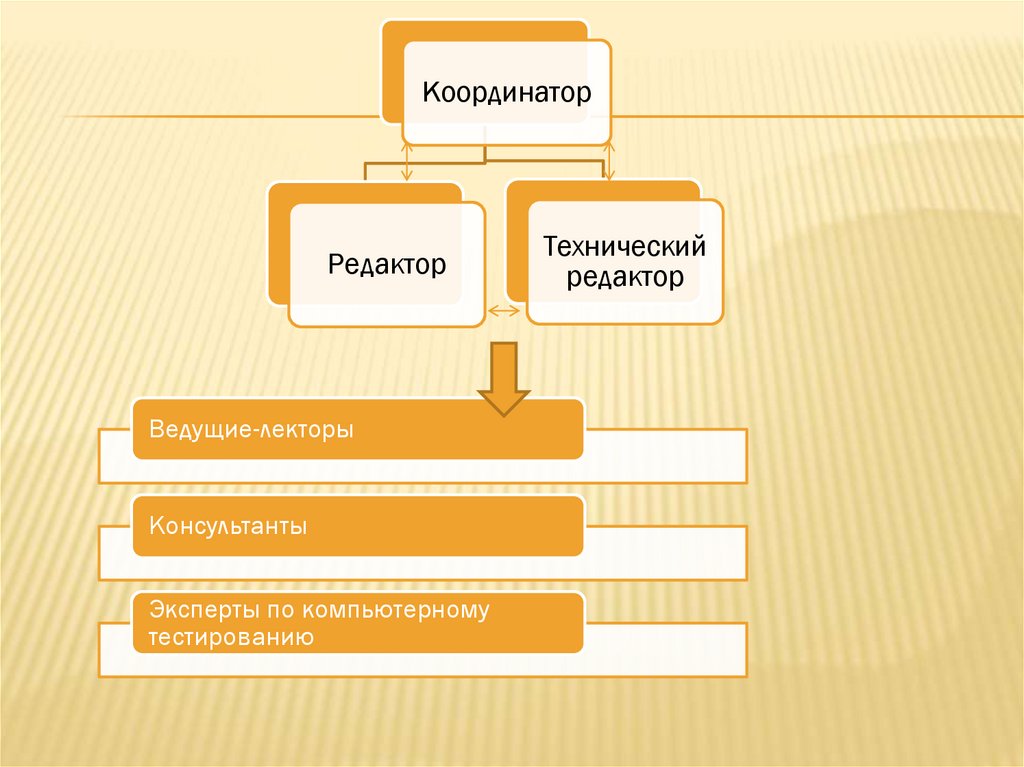
Координатор
Редактор
Ведущие-лекторы
Консультанты
Эксперты по компьютерному
тестированию
Технический
редактор

3.

I. ПОДГОТОВИТЕЛЬНЫЙ ЭТАП К ПРОВЕДЕНИЮ
ТРЕНИНГА
Повторение теории
Подбор и решение задач
Объяснение решения задач
Составление тестов
Подготовка презентаций по теории и
практике
Подготовка листов с печатной основой
Апробация этапов тренинга

4.

ПРОВЕДЕНИЕ ТРЕНИНГА
Тема: Решение задач на проценты.
Обучающая цель. Отработать умения учащихся
решать разноуровневые задачи на проценты.
Учебные задачи:
Научить учащихся распознавать ситуации, требующие
использования определённого типа задач.
Отработать объяснение решения задач в
затруднительной ситуации
Отработать навыки работы в учебных группах.
Оборудование: Компьютерный класс, проектор,
программное обеспечение, презентации.

5.

II. ПРИМЕР ЗАДАНИЙ ПРИ ПРОВЕДЕНИИ
ТРЕНИНГА
Задачи на проценты.
Определение: Процентом числа называется его сотая часть.
Пример:
1%- это одна сотая числа
1%-от числа 500 – это число 5
3%- это три сотых числа
3% от числа 500 – это число 15=500:100∙3
Решение любых задач на проценты сводится к основным трем задачам:
I – нахождение процентов от числа∙
Пример. Найти 15% от числа 60
60:100∙15=9
Или
15% - 0,15
0,15∙60=9.
Ответ: 9.
II- нахождению числа по его процентам.
Пример. Найти число 12% которого равны 30
Х-100%
Х=30∙100=250
30-12%
12
Ответ: 250
III-нахождение процентного отношения чисел.
Пример: Сколько процентов состовляет 120 от 600?
600-100%
х=120∙100 =20%
120-х%
600
Ответ: 20%

6.

Многие практические задачи, прежде всего по экономике и социологии связаны с
процентным. Оперировать понятием «проценты» необходимо любому современному
человеку. Рассмотрим несколько задач с которыми мы часто встречаемся в быту.
(Уровень «А» на экзамене) Решать успешно такие задачи должен каждый
девятиклассник.
Задача 1. Фирма покупает товар оптом по 148 рублей за 1 кг, и продает с надбавкой 20% в
розницу. Найти розничную цену товара.
I способ: 148 руб. -100%
х=148∙120; х=177,6(руб.)
Х руб..-120%
100
II способ: 120%-1,2
148∙1,2=177,6(руб.)- увеличение на 20% означает умножение на
1,2
РЕШАЕМ САМИ: до повышения цен товар стоил 300 р. Найти его стоимость после
повышения на 24%
Задача2. За депутата А проголосовало 15 человек, что составило 4% от проголосовавших от
числа голосовавших в первые 2 часа. Сколько человек проголосовало за это время?
Хч-100%
х=15∙100; х=375(ч)
15ч.-4%
4
Ответ: 375 ч.
РЕШАЕМ САМИ: 13% зарплаты отчисляется в налог. Какова зарплата если отчислено 3900
руб?
Задача3. Ученик решил 14 задач из 20. Сколько процентов задач решил ученик?
20з-100%
х=14∙100; х=70%
18з-х%
20
Ответ: 70%
РЕШАЕМ САМИ:
Сколько % от числа120 составляет число 18?
Рассмотрим две задачи, которые часто вызывают затруднения у детей и взрослых.

7.

Задача: 5
Товар стоил в июне 30 000 рублей. В июле он подорожал на 4%, а затем подешевел в августе на 4%.
Сколько стоил товар в августе?
30 000 * 1,04*0,96=29952 (руб.)
Ответ: 29952 руб..
Решаем сами. Товар стоил 200 руб. В I квартале цены увеличились на 5%, а во II снизились на 5%.
Сколько стал стоить товар?
Задачи на смеси и растворы:
Задача 5.
Сколько соли содержится в 360 граммах 10%-го раствора?
10% - й раствор обозначает, что в нем 10% - соли, 90% - воды.
360 г – 100%
Х г – 10%
Х= ;
Х= 36 г.
Ответ: 36 г. соли.
Решаем сами:
В 10% растворе сиропа 300 г. сахара.
Сколько в растворе воды?
Прежде, чем предложить вам тест, решим ещё несколько задач.
Задача 6
После уценки телевизора его новая цена составила 0,8 старой. Сколько % от старой цены составляет
новая цена?
Пусть Х р.- старая цена.
0,8*Х р- новая цена
0,8*100%=80%-новая цена от старой цены
Решаем сами:
Число ДТП в летний период составило 0,7 их числа в зимний период. На сколько % уменьшилось число
ДТП летом по сравнению с зимой?

8.

Приложение 2
Итак, переходим на более сложный уровень.
Задачи на «2» балла из второй части.
Задача 8
Сбербанк в конце года начисляет 3% к сумме, находившейся на счету. На сколько рублей увеличится вклад в
1000 рублей через 2 года?
Данная задача на «сложные проценты».
Так как величина 1000 р. будет изменяться в 2 этапа: после 1 – го года ,после 2 – го года.
1000 + 0,03 * 1000 = 1030 (руб.) по окончании 1 –го года.
1030 + 0,03 * 1030 = 1060,9 (руб.) по окончании 2 – го года.
1060,9 – 1000 = 60,9 (руб.) увеличение
Ответ: 60,9 руб.
Решаем сами: По формуле сложного процентного роста Sn=S *(1+ )n
Условие: прежнее
Зная эту формулу легко прикинуть вашу прибыль.
Задача 9
А вот данная формула помогает решать задачи на уменьшение величины:
Sn=S * (1- )
Автомобиль стоит 600 тыс. руб. Каждый год на его амортизацию списывают 10%.
Какой будет цена через 3 года?
S = 600 тыс.
Р = 10%
n = 3.
S3 = 600 т.р. * (1 - ) = 420 тыс. руб.
Решаем сами:
Через сколько лет можно списать автомобиль, т.е. Sn = 0. n - ?
Какое условие здесь не учитывается?

9.

Приложение 3
Тест. I вариант
1). На первый курс института может быть принято 180 чел. Число поданных заявлений составило 120 % от
количества мест на курсе. Сколько заявлений подано?
А) 36 б)150
в) 216 г) 300
2). От веревки длиной 12 метров отрезали 60% длины. Сколько метров осталось?
А) 4,8м б) 7,2м в) 6,4м г) 4,6 м
3). По социологическому опросу 8000 жителей городка смотрели сериал. Сколько % смотрели сериал, если в
городке 48000 жителей?
А) 12,5% б) 16% в) 29% г) 16 2/3%
4).Некоторый товар поступил в продажу по цене 100 рублей. Каждые 2 недели цена товара снижается на 15%.
Сколько будет стоить товар на 23 день, если не будет куплен?
А) 85 р. б) 72, 25р. в) 15 р. Г). 96 р.
5). На счет в банке, доход по которому составляет 20 % годовых, внесли а рублей. Какая сумма будет на счету
через год?
А) а+0,2а б). а+20а в).0,2а г). а+20
Тест. II вариант
1). В декабре каждому сотруднику предприятия выплатили премию, составившую 130% от зарплаты за 1 месяц.
Какую премию получил сотрудник, если его зарплата 5500р ?
А) 71500р б) 7150р в) 5630р г) 1650р
2). Мороженое «Пломбир» содержит 16% сахара, что составляет 40г. Сколько весит мороженое?
А) 240г б) 250г в) 200г д)6,4кг
3) По социологическому опросу 6000 жителей городка смотрели футбол. Сколько % смотрят футбол, если в
городке 48000 жителей?
А) 12,5% б) 16% в) 29% г) 16 2/3 %
4).В магазин поступил товар по цене 120 р. Цена товара снижается каждую неделю на 5%. Сколько будет стоить
товар на 9-й день, если не будет куплен?
А).115р б) 114р в)108,3р г) 6 р.
5)На счет в банке, доход по которому составляет 3% годовых, внесли а рублей. Какая сумма будет на счету через
год?
А). а-0,03 а б) а+0,03а в) 0,03а г) а

10.

Ответы к тесту
1 вариант
1в
2а
3г
4а
5а
2 вариант
1б
2б
3а
4б
5б

11.

Ответы к задачам
1. 300р.-100%
х=300∙124
х=372(р)
Хр.-124%
100
Ответ:372
Или: 300∙1,24=372 р.
2. Х-100%
х=3900∙100; х=30000 (р)
3900-13%
13
Ответ:30000р.
3. 120-100%
х=100∙18; х=15%
18-х%
120
Ответ:х=15%
4. А
1). Какую часть 6 составляет от 8? 6:8=0,75
2). На какую часть 6 меньше, чем 8? 1-0,75=0.25
3). На сколько % 6 меньше 8?
0,25∙100=25%
Ответ: на 25%.
Б)
1).Во сколько раз 8 больше чем 6?
8:6= 1 1/3
2). На какую часть 8 больше чем 6? 1 1/3 -1= 1/3
3). На сколько % 8 больше чем 6? 1/3 100=0,3333333∙100%=33,333=33 1/3
Ответ: 33 1/3
5. 200 * 1,05 * 0,95=199,5 (р)
Ответ: 199,5 руб.

12.

6. 10% р-р. сиропа обозначает 10% - сиропа, 90% - воды
I. Х г. – 100%
300 г. – 10%
Х= ;
Х=3000 (г) – весь сироп.
II. 3000 – 300=2700 (г) – вода.
Ответ: воды – 2700 г.
7. Пусть Х – число ДТП зимой.
0,7 * Х – летом
Х – 0,7*Х=0,3*Х.
0,3 – это 30%.
Уменьшилось на 30%.
8. I Х+0,5*Х=1,5Х жителей
II 2Х жителей
2Х>1,5X. Во втором доме >.
9. S2=1000 * (1+ )2 = 1060,9 (р)
10. 600 * (1 - ) = 0. 1 - = 0. 10*n = 100
n = 10
Ответ: через 10 лет.
Не учитывается условие 600 т.р.
11.
1)
2)
Ответ: 40%

13.

ЗАКЛЮЧЕНИЕ
Выбор данной формы проведения
внеклассного занятия позволил:
повторить учащимися старших классов
темы «Решение задач на проценты».
выработать у учащихся старших классов
умение выступать перед аудиторией.
При анализе входного и выходного
тестирования знаний было выявлено
значительное улучшение качественных
показателей по данной теме.