Similar presentations:
Образец оформления задач
1.
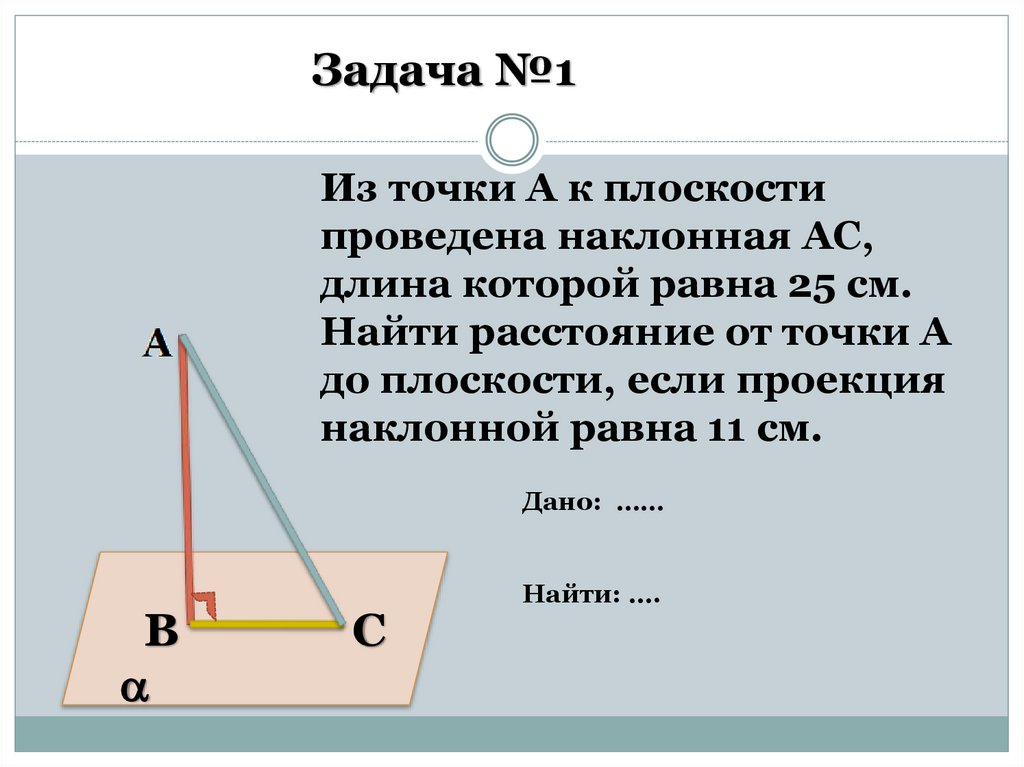
Задача №1Из точки А к плоскости
проведена наклонная АС,
длина которой равна 25 см.
Найти расстояние от точки А
до плоскости, если проекция
наклонной равна 11 см.
Дано: ……
В
С
Найти: ….
2.
Задача №1Решение
Рассмотрим ∆ АВС, ےВ = 90◦
По теореме Пифагора АС2 = АВ2 + ВС2
АВ2 = 252 – 112 = 625 – 121 = √504
АВ = √504 см
Ответ : АВ = √504 см
3.
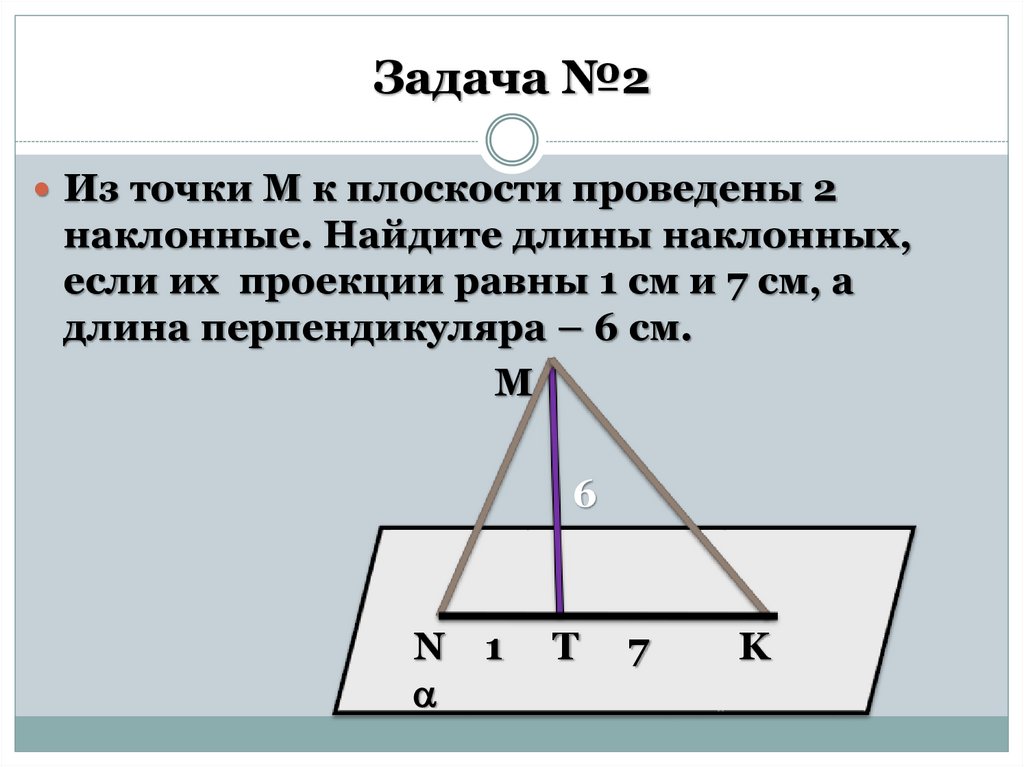
Задача №2Из точки М к плоскости проведены 2
наклонные. Найдите длины наклонных,
если их проекции равны 1 см и 7 см, а
длина перпендикуляра – 6 см.
М
6
N
1
T
7
K
4.
Задача №2Рассмотрим ∆ MTN, ےT = 90◦
По теореме Пифагора MN2 = MT2 + NT2
MN2 = 12 + 62 = 1 + 36 = 37
MN =
см
Рассмотрим ∆ MTK, ےT = 90◦
По теореме Пифагора MK2 = MT2 + KT2
MK2 = 72 + 62 = 49 + 36 = 85
MK =
см
Ответ : MN =
см, MK =
см
5.
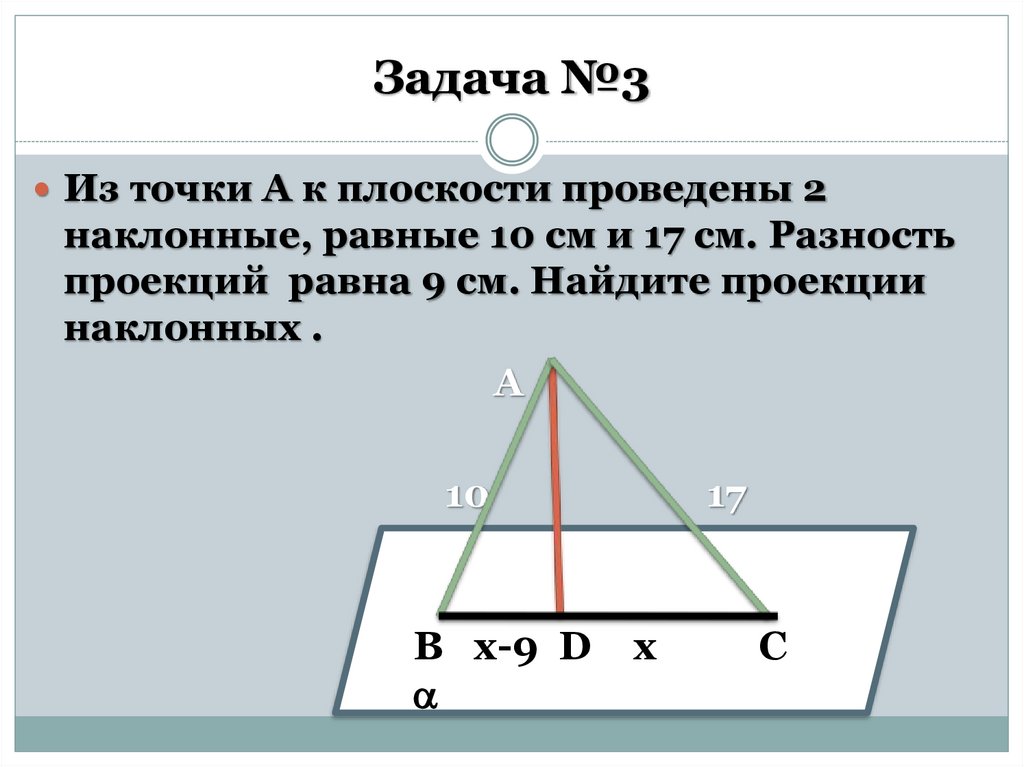
Задача №3Из точки А к плоскости проведены 2
наклонные, равные 10 см и 17 см. Разность
проекций равна 9 см. Найдите проекции
наклонных .
A
10
В х-9 D
17
х
C
6.
Задача №3Рассмотрим ∆ АДВ, ےД = 90◦
По теореме Пифагора АВ2 = ВД2 + АД2
АД2 = 102 − (х – 9)2
Рассмотрим ∆ АДС, ےД = 90◦
По теореме Пифагора АС2 = АД2 + ДС2
АД2 = 172 − х 2
Так как АД общая , то
100 - (х – 9)2 = 289 – х2
100 - х2 + 18х - 81= 289 – х2
18х= 289 – 100 + 81
х = 15
ДС = 15 см ВД = 15 – 9 = 6 см
Ответ : ДС = 15 см, ВД = 6 см
7.
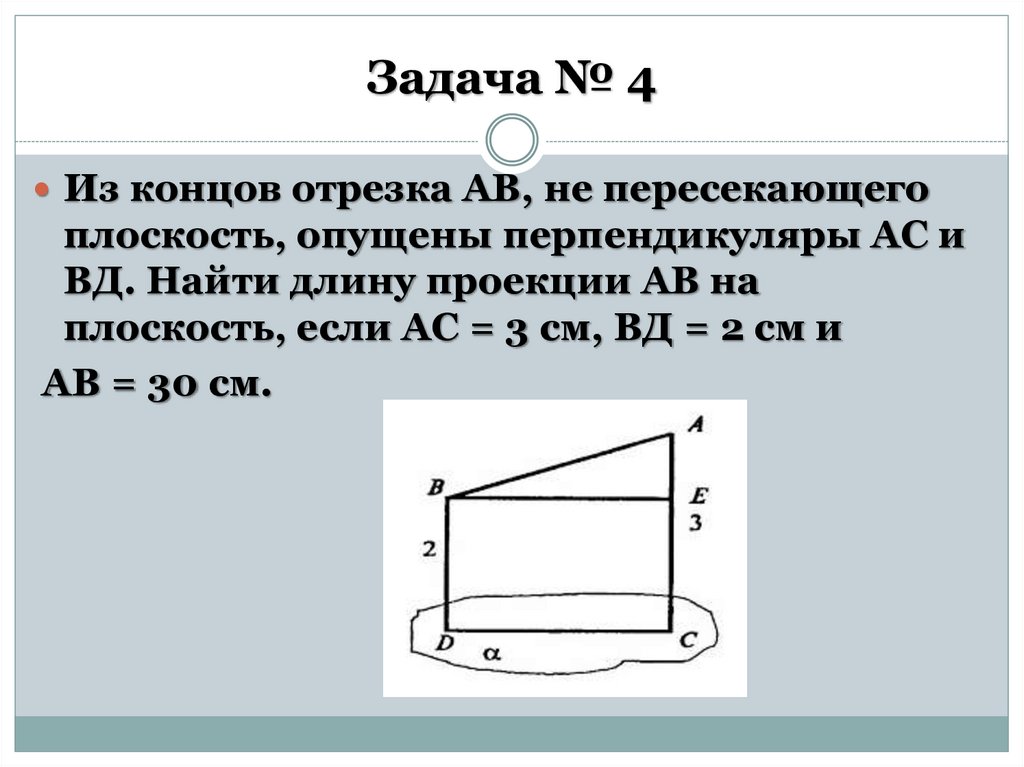
Задача № 4Из концов отрезка АВ, не пересекающего
плоскость, опущены перпендикуляры АС и
ВД. Найти длину проекции АВ на
плоскость, если АС = 3 см, ВД = 2 см и
АВ = 30 см.
8.
Задача № 4Проведем ВЕ ‖ СД
Рассмотрим ∆ АЕВ, ےЕ= 90◦
По теореме Пифагора АВ2 = ВЕ2 + АЕ2
ВЕ2 = 302 − 12 = 900 – 1 = 899
ВЕ = СД = √899 см
Ответ : СД = √899 см
9.
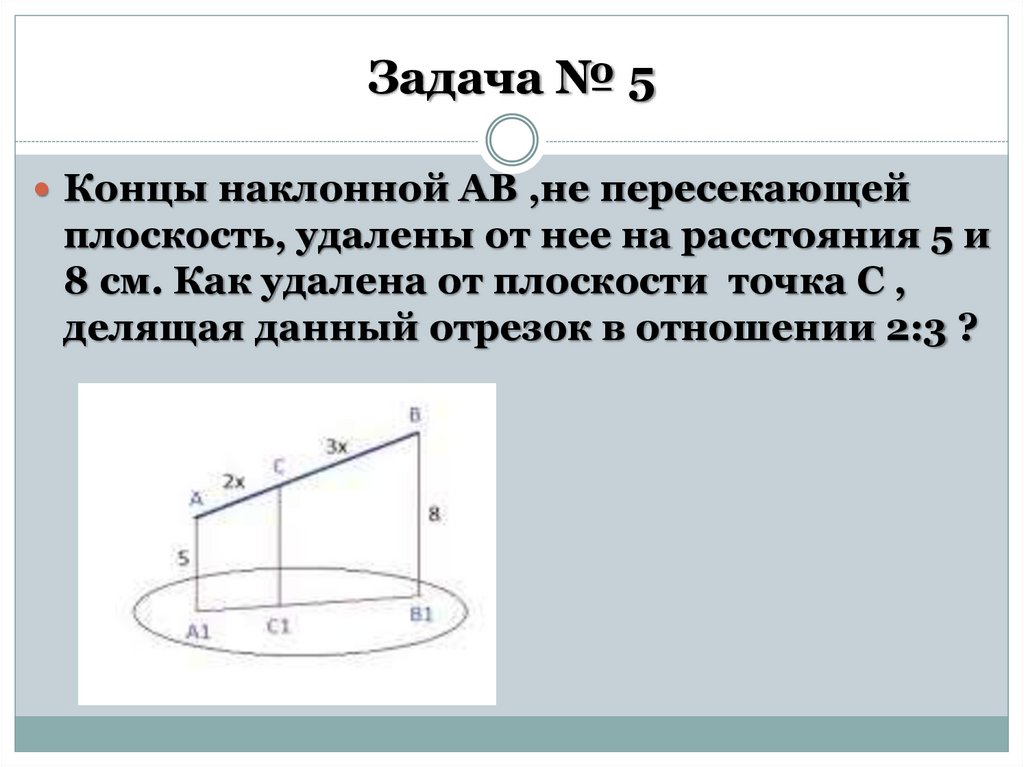
Задача № 5Концы наклонной АВ ,не пересекающей
плоскость, удалены от нее на расстояния 5 и
8 см. Как удалена от плоскости точка С ,
делящая данный отрезок в отношении 2:3 ?
10.
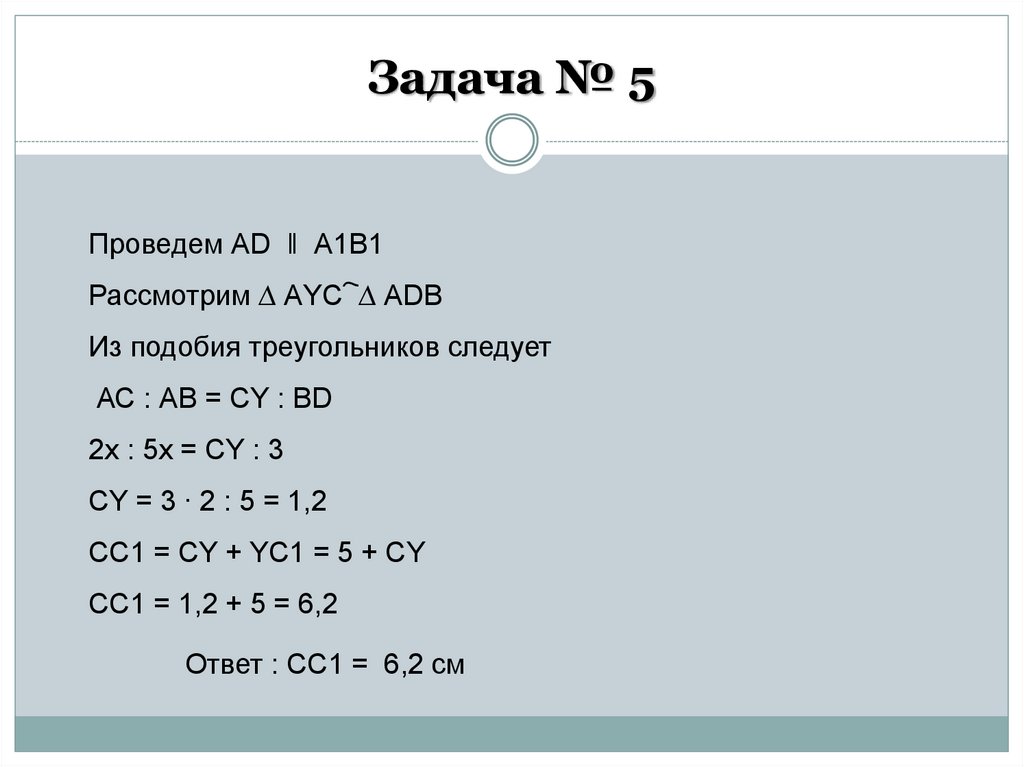
Задача № 5Проведем АD ‖ А1В1
Рассмотрим ∆ АYС ҇ ∆ АDВ
Из подобия треугольников следует
АС : АВ = СY : ВD
2х : 5х = СY : 3
СY = 3 ∙ 2 : 5 = 1,2
СС1 = CY + YC1 = 5 + СY
СС1 = 1,2 + 5 = 6,2
Ответ : СС1 = 6,2 см




 mathematics
mathematics








