Кривые Безье

1.

Кривые Безье

2.

Кривая Безье задаётся опорными точками. Их может быть две, три, четыре или
больше.

3.

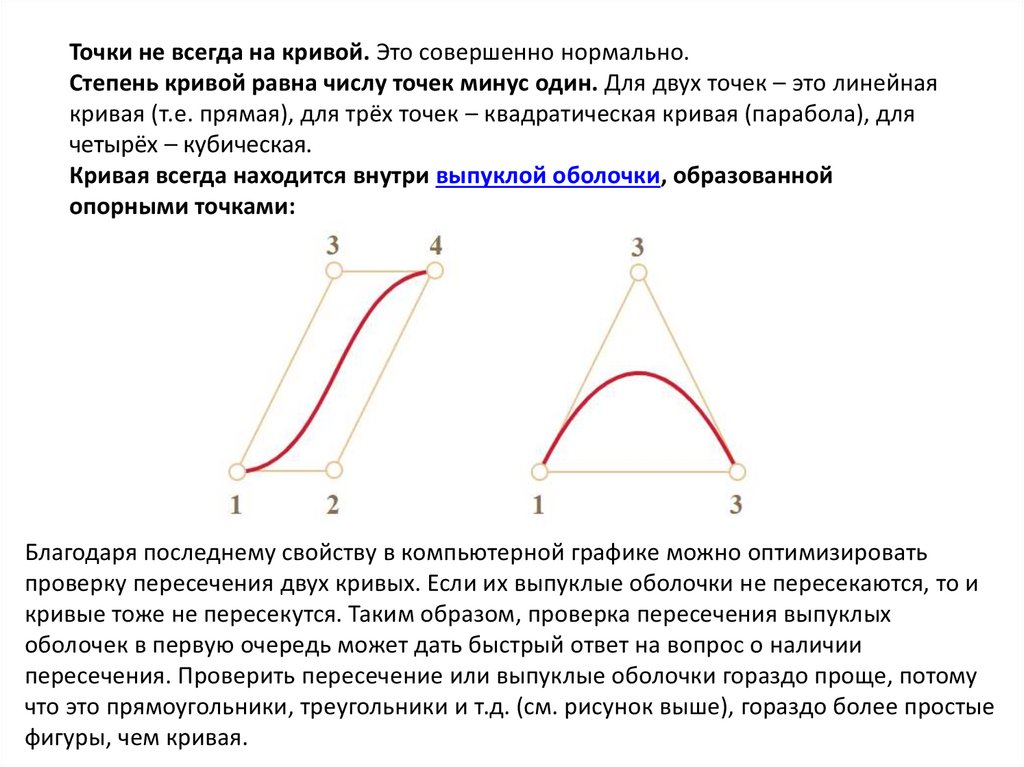
Точки не всегда на кривой. Это совершенно нормально.
Степень кривой равна числу точек минус один. Для двух точек – это линейная
кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для
четырёх – кубическая.
Кривая всегда находится внутри выпуклой оболочки, образованной
опорными точками:
Благодаря последнему свойству в компьютерной графике можно оптимизировать
проверку пересечения двух кривых. Если их выпуклые оболочки не пересекаются, то и
кривые тоже не пересекутся. Таким образом, проверка пересечения выпуклых
оболочек в первую очередь может дать быстрый ответ на вопрос о наличии
пересечения. Проверить пересечение или выпуклые оболочки гораздо проще, потому
что это прямоугольники, треугольники и т.д. (см. рисунок выше), гораздо более простые
фигуры, чем кривая.

4.

Построение кривой Безье с 3 точками по «алгоритму де Кастельжо»:
1. Рисуются опорные точки. В примере это: 1, 2, 3.
2. Строятся отрезки между опорными точками в следующем порядке 1 → 2 → 3. На
рисунке они коричневые.
3. Параметр t «пробегает» значения от 0 до 1. В примере использован шаг 0.05, т.е. в
цикле 0, 0.05, 0.1, 0.15, ... 0.95, 1.
Для каждого из этих значений t:
На каждом из коричневых отрезков берётся точка, находящаяся на
расстоянии, пропорциональном t, от его начала. Так как отрезков два, то и
точек две.
Например, при t=0 – точки будут в начале, при t=0.25 – на расстоянии в 25%
от начала отрезка, при t=0.5 – 50% (на середине), при t=1 – в конце
отрезков.
Эти точки соединяются. На рисунке ниже соединяющий их отрезок
изображён синим.

5.

6.

4. На получившемся синем отрезке берётся точка на расстоянии,
соответствующем t. То есть, для t=0.25 (левый рисунок) получаем точку в конце
первой четверти отрезка, для t=0.5 (правый рисунок) – в середине отрезка. На
рисунках выше эта точка отмечена красным.
5. По мере того, как t «пробегает» последовательность от 0 до 1, каждое
значение t добавляет к кривой точку. Совокупность таких точек для всех значений
образует кривую Безье. Она красная и имеет параболическую форму на картинках
выше.

7.

Был описан процесс для построения по трём точкам. Но то же самое
происходит и с четырьмя точками.

8.

Виды кривых Безье
Линейные кривые
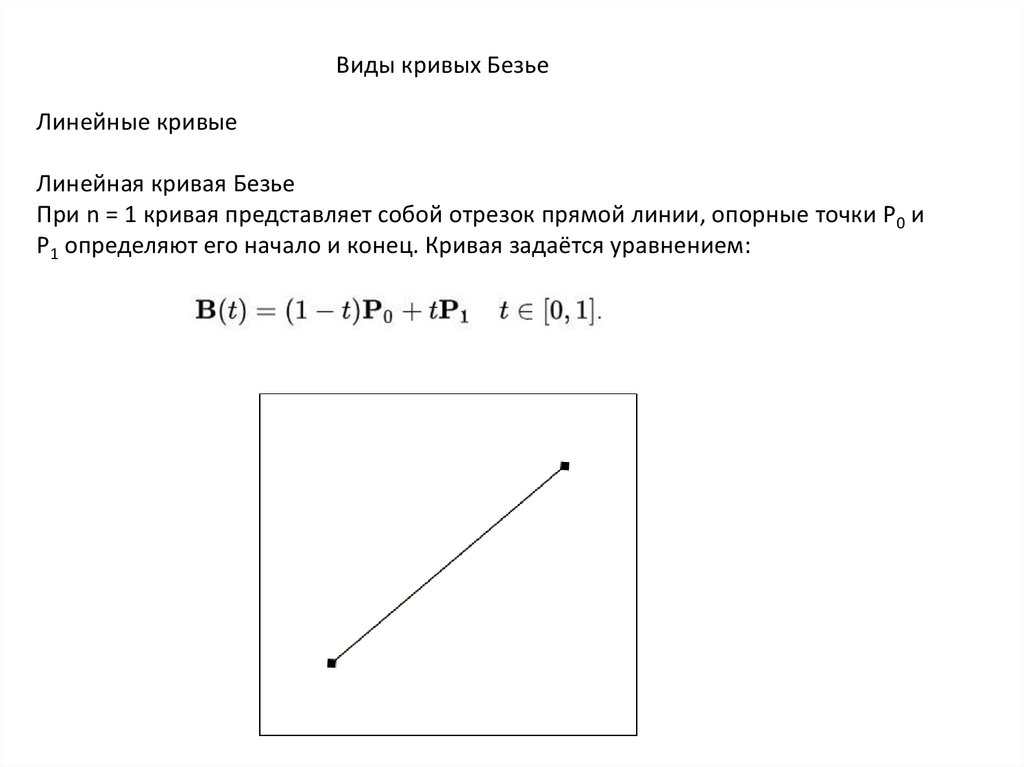
Линейная кривая Безье
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и
P1 определяют его начало и конец. Кривая задаётся уравнением:

9.

Виды кривых Безье
Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: P0, P1 и P2.

10.

Виды кривых Безье
Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим
уравнением

11.

Свойства кривой Безье
• непрерывность заполнения сегмента между начальной и
конечной точками;
• кривая всегда располагается внутри фигуры, образованной
линиями, соединяющими контрольные точки;
• при наличии только двух контрольных точек сегмент
представляет собой прямую линию;
• прямая линия образуется при коллинеарном (на одной
прямой) размещении управляющих точек;
• кривая Безье симметрична, то есть обмен местами между
начальной и конечной точками (изменение направления
траектории) не влияет на форму кривой;
• масштабирование и изменение пропорций кривой Безье не
нарушает её стабильности, поскольку с математической точки
зрения она «аффинно инвариантна»;
• изменение координат хотя бы одной из точек ведет к
изменению формы всей кривой Безье;

12.

Свойства кривой Безье
• любой частичный отрезок кривой Безье также является
кривой Безье;
• степень (порядок) кривой всегда на одну ступень меньше
числа контрольных точек. Например, при трёх контрольных
точках форма кривой — парабола, так как парабола — кривая
2-го порядка;
• окружность не может быть описана параметрическим
уравнением кривой Безье;
• невозможно создать параллельные кривые Безье, за
исключением тривиальных случаев (прямые линии и
совпадающие кривые), хотя существуют алгоритмы, строящие
приближённую параллельную кривую Безье с приемлемой
для практики точностью.

13.

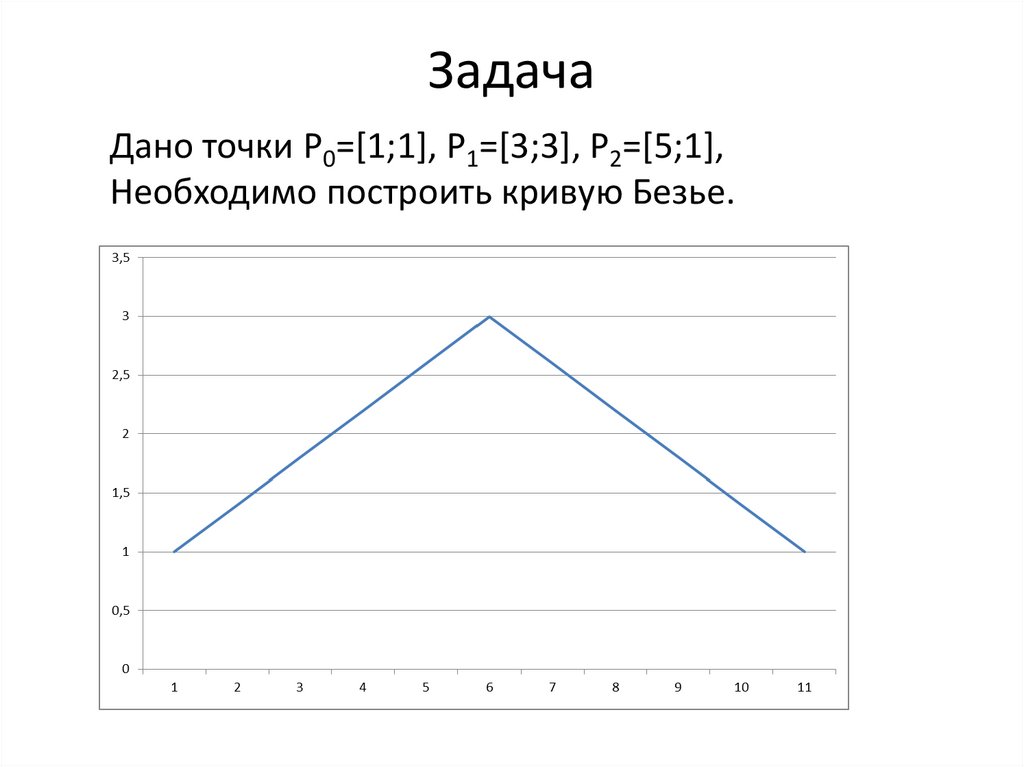
Задача
Дано точки P0=[1;1], P1=[3;3], P2=[5;1],
Необходимо построить кривую Безье.

14.

Решение
Возьмем t с шагом 0,1
t=[0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1]

15.

Решение
Возьмем t с шагом 0,1
t=[0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1]
t=0
x(0)=(1-0)2*1+2*0*(1-0)*3+02*5=1
y(0)=(1-0)2*1+2*0*(1-0)*3+02*1=1
t=0,1
x(0)=(1-0,1)2*1+2*0,1*(1-0,1)*3+0,12*5=1,4
y(0)=(1-0,1)2*1+2*0,1*(1-0,1)*3+0,12*1=1,36

16.

Решение
t
x
y
0,1
1,4
1,36
0,2
1,8
1,64
0,3
2,2
1,84
0,4
2,6
1,96
0,5
3
2
0,6
3,4
1,96
0,7
3,8
1,84
0,8
4,2
1,64
0,9
4,6
1,36
1
5
1

17.

Решение