Образовательный портал «Решу ЕГЭ»

1.

Образовательный портал «РЕШУ ЕГЭ» —
математика профильная
Вариант № 73723696
Образовательный портал «РЕШУ ЕГЭ» —
математика профильная
Вариант № 73723696
7. Тип 7 № 77401
1. Тип 1 № 27922
Сто­ро­на AB тре­уголь­ни­ка ABC c тупым углом C
равна ра­ди­у­су опи­сан­ной около него окруж­но­сти. Най­ди­те угол C. Ответ дайте в гра­ду­сах.
Най­ди­те зна­че­ние вы­ра­же­ния
если
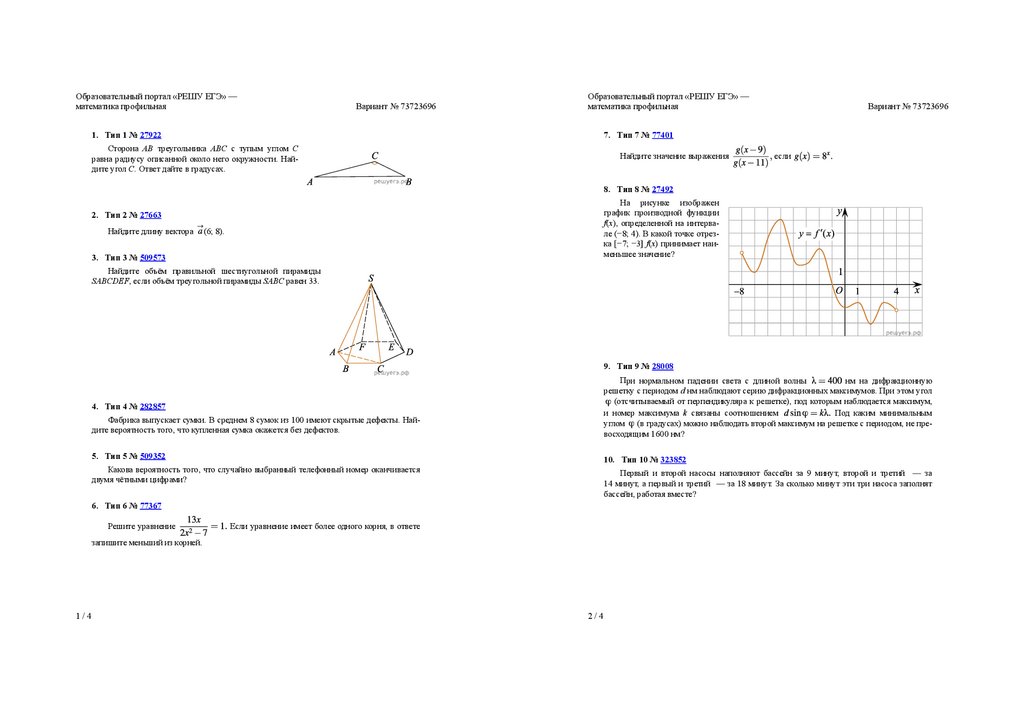
8. Тип 8 № 27492
На ри­сун­ке изоб­ра­жен
гра­фик про­из­вод­ной функ­ции
f(x), опре­де­лен­ной на ин­тер­ва­ле (−8; 4). В какой точке от­рез­ка [−7; −3] f(x) при­ни­ма­ет наи­мень­шее зна­че­ние?
2. Тип 2 № 27663
Най­ди­те длину век­то­ра
(6; 8).
3. Тип 3 № 509573
Най­ди­те объём пра­виль­ной ше­сти­уголь­ной пи­ра­ми­ды
SABCDEF, если объём тре­уголь­ной пи­ра­ми­ды SABC равен 33.
9. Тип 9 № 28008
Фаб­ри­ка вы­пус­ка­ет сумки. В сред­нем 8 сумок из 100 имеют скры­тые де­фек­ты. Най­ди­те ве­ро­ят­ность того, что куп­лен­ная сумка ока­жет­ся без де­фек­тов.
При нор­маль­ном па­де­нии света с дли­ной волны
нм на ди­фрак­ци­он­ную
решeтку с пе­ри­о­дом d нм на­блю­да­ют серию ди­фрак­ци­он­ных мак­си­му­мов. При этом угол
(от­счи­ты­ва­е­мый от пер­пен­ди­ку­ля­ра к решeтке), под ко­то­рым на­блю­да­ет­ся мак­си­мум,
и номер мак­си­му­ма k свя­за­ны со­от­но­ше­ни­ем
Под каким ми­ни­маль­ным
углом (в гра­ду­сах) можно на­блю­дать вто­рой мак­си­мум на решeтке с пе­ри­о­дом, не пре­вос­хо­дя­щим 1600 нм?
5. Тип 5 № 509352
10. Тип 10 № 323852
Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но вы­бран­ный те­ле­фон­ный номер окан­чи­ва­ет­ся
двумя чётными циф­ра­ми?
Пер­вый и вто­рой на­со­сы на­пол­ня­ют бас­сейн за 9 минут, вто­рой и тре­тий — за
14 минут, а пер­вый и тре­тий — за 18 минут. За сколь­ко минут эти три на­со­са за­пол­нят
бас­сейн, ра­бо­тая вме­сте?
4. Тип 4 № 282857
6. Тип 6 № 77367
Ре­ши­те урав­не­ние
Если урав­не­ние имеет более од­но­го корня, в от­ве­те
за­пи­ши­те мень­ший из кор­ней.
1/4
2/4

2.

Образовательный портал «РЕШУ ЕГЭ» —
математика профильная
Вариант № 73723696
Образовательный портал «РЕШУ ЕГЭ» —
математика профильная
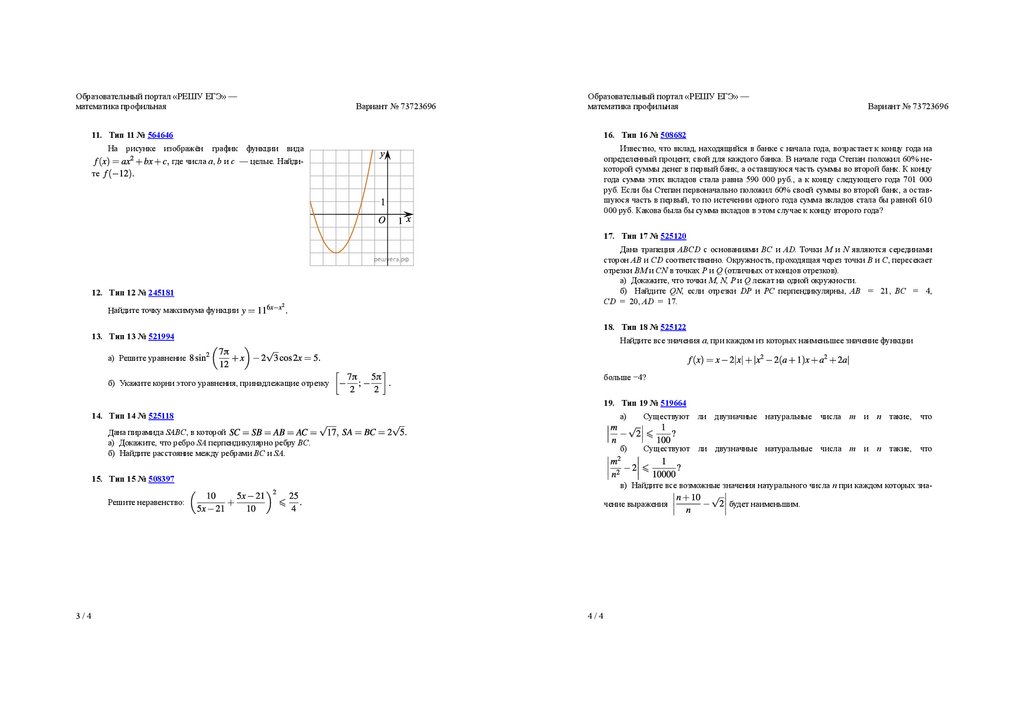
11. Тип 11 № 564646
Вариант № 73723696
16. Тип 16 № 508682
На ри­сун­ке изоб­ражён гра­фик функ­ции вида
Из­вест­но, что вклад, на­хо­дя­щий­ся в банке с на­ча­ла года, воз­рас­та­ет к концу года на
опре­де­лен­ный про­цент, свой для каж­до­го банка. В на­ча­ле года Сте­пан по­ло­жил 60% не­ко­то­рой суммы денег в пер­вый банк, а остав­шу­ю­ся часть суммы во вто­рой банк. К концу
года сумма этих вкла­дов стала равна 590 000 руб., а к концу сле­ду­ю­ще­го года 701 000
руб. Если бы Сте­пан пер­во­на­чаль­но по­ло­жил 60% своей суммы во вто­рой банк, а остав­шу­ю­ся часть в пер­вый, то по ис­те­че­нии од­но­го года сумма вкла­дов стала бы рав­ной 610
000 руб. Ка­ко­ва была бы сумма вкла­дов в этом слу­чае к концу вто­ро­го года?
где числа a, b и c — целые. Най­ди­те
17. Тип 17 № 525120
Дана тра­пе­ция ABCD с ос­но­ва­ни­я­ми BC и AD. Точки M и N яв­ля­ют­ся се­ре­ди­на­ми
сто­рон AB и CD со­от­вет­ствен­но. Окруж­ность, про­хо­дя­щая через точки B и С, пе­ре­се­ка­ет
от­рез­ки BM и CN в точ­ках P и Q (от­лич­ных от кон­цов от­рез­ков).
а) До­ка­жи­те, что точки M, N, P и Q лежат на одной окруж­но­сти.
б) Най­ди­те QN, если от­рез­ки DP и PC пер­пен­ди­ку­ляр­ны, AB = 21, BC = 4,
CD = 20, AD = 17.
12. Тип 12 № 245181
Най­ди­те точку мак­си­му­ма функ­ции
18. Тип 18 № 525122
13. Тип 13 № 521994
Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых наи­мень­шее зна­че­ние функ­ции
а) Ре­ши­те урав­не­ние
боль­ше −4?
б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку
19. Тип 19 № 519664
14. Тип 14 № 525118
Дана пи­ра­ми­да SABC, в ко­то­рой
а) До­ка­жи­те, что ребро SA пер­пен­ди­ку­ляр­но ребру BC.
б) Най­ди­те рас­сто­я­ние между реб­ра­ми BC и SA.
15. Тип 15 № 508397
Су­ще­ству­ют ли дву­знач­ные на­ту­раль­ные числа m и n такие, что
б)
Су­ще­ству­ют ли дву­знач­ные на­ту­раль­ные числа m и n такие, что
в) Най­ди­те все воз­мож­ные зна­че­ния на­ту­раль­но­го числа n при каж­дом ко­то­рых зна­-
Ре­ши­те не­ра­вен­ство:
3/4
а)
че­ние вы­ра­же­ния
4/4
будет наи­мень­шим.