Similar presentations:
Выборочное наблюдение. Лекция № 7
1. ЛЕКЦИЯ № 7
Астафурова И.С.2. Компетенции:
Распространение результатовнесплошного наблюдения на всю
совокупность на основе:
построения границ для средней величины
признака в генеральной совокупности на
основе данных выборочной совокупности.;
построения границ значений для доли
единиц, обладающих определённым
свойством, в основной совокупности на
основе данных выборочной совокупности.
Астафурова И.С.
3. § 1. Основные понятия, классификации, обозначения
Астафурова И.С.4.
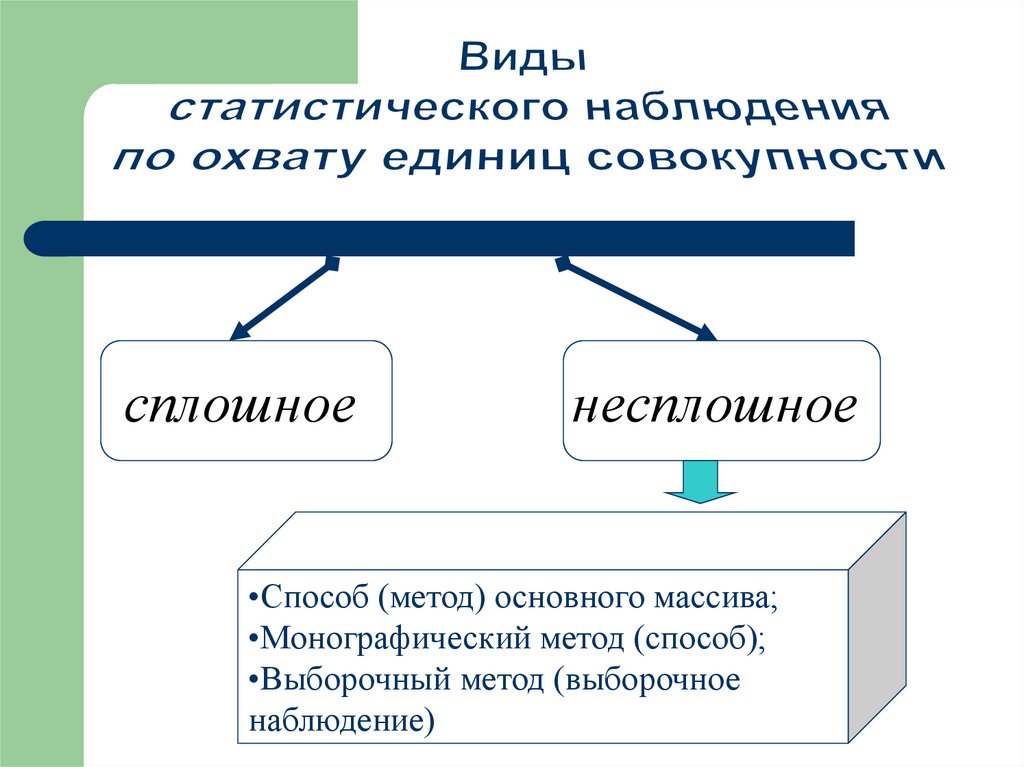
сплошноенесплошное
•Способ (метод) основного массива;
•Монографический метод (способ);
•Выборочный метод (выборочное
наблюдение)Астафурова И.С.
5. Для исследования части единиц совокупности (проведения несплошного наблюдения) используются три метода:
метод основного массива,выборочный метод
монографический метод.
Астафурова И.С.
6. метод основного массива
состоит в отборе наиболеекрупных единиц совокупности в
выборочную совокупность,
обладающих изучаемым
свойством.
Астафурова И.С.
7. выборочный метод
представляет собой метод несплошногонаблюдения, при котором отбор из основной
совокупности выполняется в случайном порядке,
в соответствии с научными принципами теории
выборочного метода. Основные принципы
выборочного метода – случайность отбора
(равной возможности попадания в выборку) и
репрезентативность, представительство по всем
признакам изучаемой совокупности.
Астафурова И.С.
8. монографический метод
представляет собой отбор одной илинескольких единиц совокупности,
подвергающихся более тщательному
изучению их свойств.
Астафурова И.С.
9.
Выборочное наблюдение несплошное наблюдение,при котором отбор
подлежащих обследованию
единиц осуществляется в
случайном порядке,
отобранная часть изучается, а
результаты распространяются на
всю совокупность (множество)
единиц
Астафурова И.С.
10. ПРИЧИНЫ:
Экономия времени и средств;Сведение к минимуму порчи и
уничтожения исследуемых объектов;
Необходимость детального
исследования каждой единицы
совокупности;
Достижение большой точности
результатов исследования, благодаря
сокращению ошибок
Астафурова И.С.
11.
Астафурова И.С.12.
ОшибкиАстафурова И.С.
13. Ошибки регистрации
Случайные(непреднамеренные);
Систематические
(тенденциозные)
Астафурова И.С.
14.
Ошибкирепрезентативности
Астафурова И.С.
15. Ошибка выборки (репрезентативности)- разница между значением показателя, полученного по выборке и генеральным параметром.
Ошибка выборки(репрезентативности)разница между значением
показателя, полученного по
выборке и генеральным
параметром. Ошибка выборки
оценивается в зависимости от
метода отбора повторного
или бесповторного.
16. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
ВСЯ СОВОКУПНОСТЬРЕАЛЬНО СУЩЕСТВУЮЩИХ
ЕДИНИЦ, ЯВЛЯЮЩИХСЯ
СТАТИСТИЧЕСКОЙ
СОВОКУПНОСТЬЮ
ДЛЯ ИЗУЧАЕМОГО
ЯВЛЕНИЯ ИЛИ ПРОЦЕССА
Астафурова И.С.
17. ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
СОВОКУПНОСТЬЕДИНИЦ, ОТОБРАННЫХ
ИЗ ГЕНЕРАЛЬНОЙ
ПО ОПРЕДЕЛЕННЫМ
ПРАВИЛАМ
Астафурова И.С.
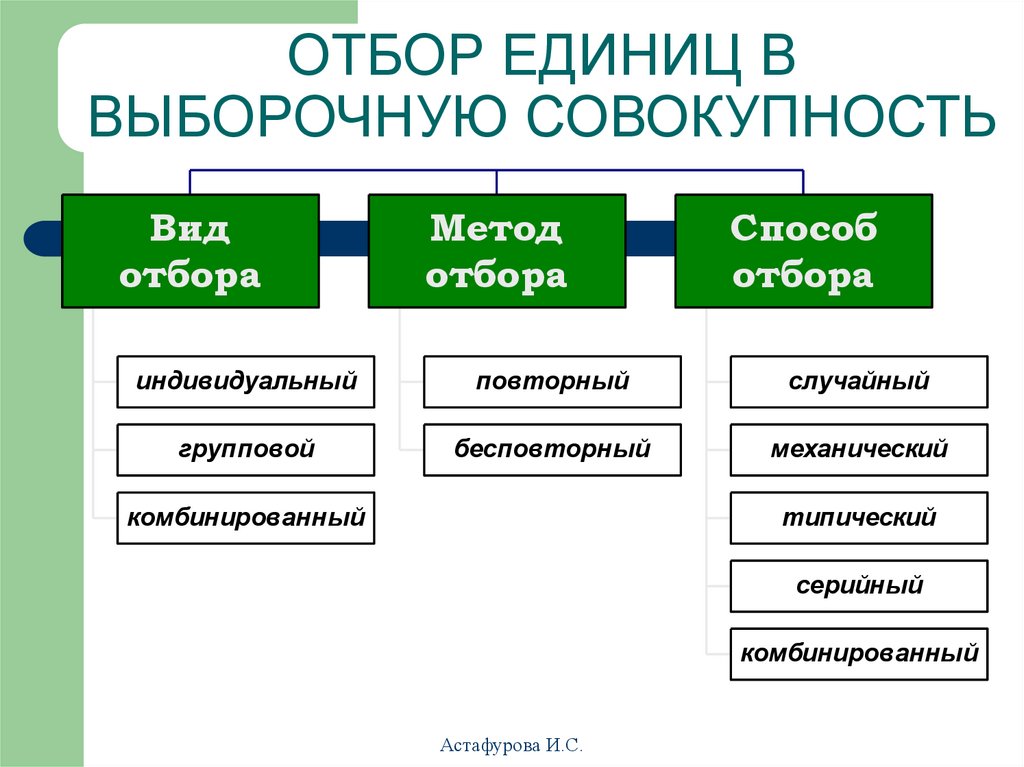
18. ОТБОР ЕДИНИЦ В ВЫБОРОЧНУЮ СОВОКУПНОСТЬ
Видотбора
Метод
отбора
Способ
отбора
индивидуальный
повторный
случайный
групповой
бесповторный
механический
комбинированный
типический
серийный
комбинированный
Астафурова И.С.
19. § 2. Распространение результатов несплошного наблюдения на генеральную совокупность.
Астафурова И.С.20. ОСНОВНАЯ ЗАДАЧА ОРГАНИЗАЦИИ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ -ОЦЕНКА РЕПРЕЗЕНТАТИВНОСТИ (ПРЕДСТАВИТЕЛЬНОСТИ) ВЫБОРОЧНОЙ СОВОКУПНОСТИ С
ПОМОЩЬЮОШИБКИ
Астафурова И.С.
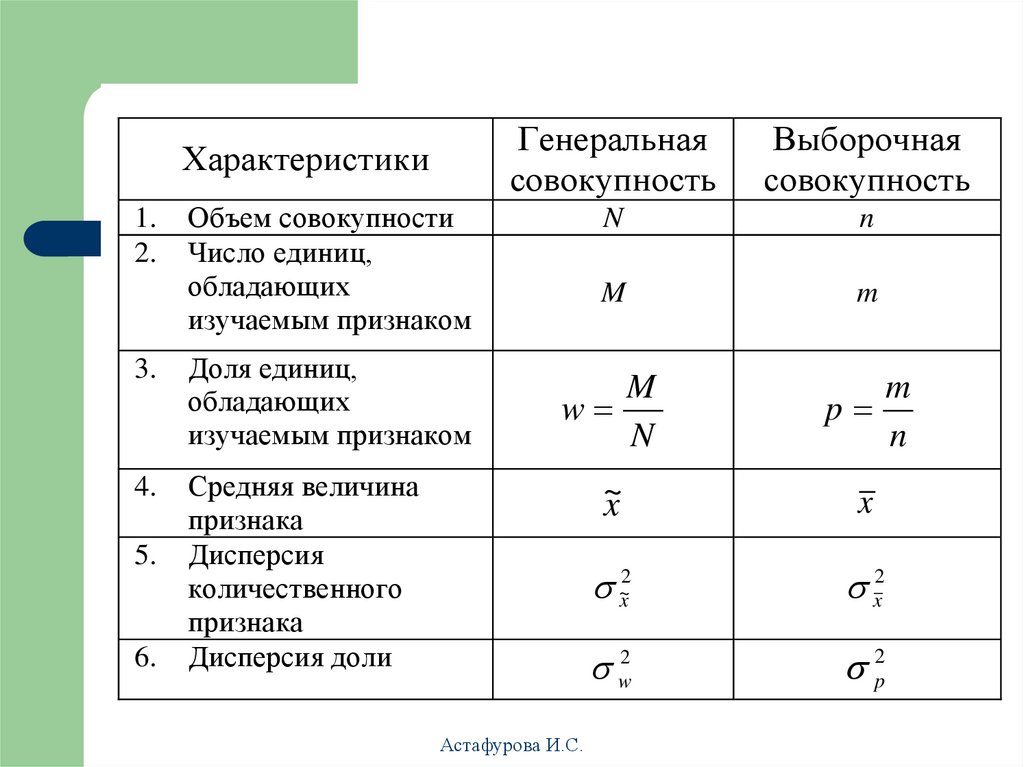
21. Обозначения основных характеристик генеральной и выборочной совокупностей
Астафурова И.С.22.
Характеристики1.
2.
Доля единиц,
обладающих
изучаемым признаком
4.
Средняя величина
признака
Дисперсия
количественного
признака
Дисперсия доли
6.
Выборочная
совокупность
N
n
M
m
M
w
N
m
p
n
~
x
x
~x2
x2
w2
2p
Объем совокупности
Число единиц,
обладающих
изучаемым признаком
3.
5.
Генеральная
совокупность
Астафурова И.С.
23. Генеральные и выборочные параметры
~x - генеральная средняя
x - выборочная средняя
M
- генеральная доля
N
m
p - выборочная доля
n
24.
Очевидно, что генеральный и выборочный параметры отличаются друг отдруга: предельная ошибка выборочной средней x ~
x x ,а предельная ошибка
выборочной доли р p где x, p - значения средней величины и доли для
выборочной совокупности, ~
x , - значения средней величины и доли генеральной
x x x ; p p .
совокупности, отсюда: ~
25. ПРЕДЕЛЬНАЯ ОШИБКА ВЫБОРКИ ДЛЯ ГЕНЕРАЛЬНОЙ СРЕДНЕЙ
~x xx
x t Sx
Астафурова И.С.
26. Таблица некоторых значений функции Лапласа
tФ(t)
1
0,683
2
0,954
~
Ф( t ) P( x x )
Астафурова И.С.
3
0,997
27. СРЕДНЯЯ ОШИБКА ВЫБОРКИ ДЛЯ ГЕНЕРАЛЬНОЙ СРЕДНЕЙ
2повторный
отбор
n
Sx
2
n бесповторный
1
n N отбор
Астафурова И.С.
28. ПРЕДЕЛЬНАЯ ОШИБКА ВЫБОРКИ ДЛЯ ГЕНЕРАЛЬНОЙ ДОЛИ
p pp t Sp
m
p
n
Астафурова И.С.
29. СРЕДНЯЯ ОШИБКА ВЫБОРКИ ДЛЯ ГЕНЕРАЛЬНОЙ ДОЛИ
p (1 p)повторный отбор
n
Sp
бесповторный
p (1 p) 1 n отбор
n
N
Астафурова И.С.
30. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ГЕНЕРАЛЬНЫХ ПАРАМЕТРОВ
~x x x x x
генеральная средняя
p p p p
генеральная доля
Астафурова И.С.
31.
МАЛАЯ ВЫБОРКАПри объемах выборки, не
превышающих 30 единиц,
средняя ошибка выборки:
Sx
n 1
2
Астафурова И.С.
32. ОПРЕДЕЛЕНИЕ ЧИСЛЕННОСТИ ВЫБОРКИ
Метод отбораПовторный
Бесповторный
Формулы объема выборки
для средней
для доли
n
n
t 2 2
2
t N
2 2
N 2 t 2 2
Астафурова И.С.
t p (1 p )
n
2
2
t 2 p(1 p) N
n 2 2
N t p(1 p)
33.
Астафурова И.С.34.
С целью изучения занятости населения города напредприятиях проведена 5%-ная механическая выборка,
в результате которой получено следующее
распределение предприятий по численности
работников:
Группы по
численности
работников, чел.
До
25
25
50
50
75
75
100
100
и выше
Астафурова И.С.
Число
предприятий
15
20
35
25
5
35.
1. С вероятностью 0,997 определитьошибку выборочной средней и
возможные границы, в которых
ожидается средняя численность на
предприятиях города.
2. С вероятностью 0,954 предельную
ошибку выборочной доли и границы
удельного веса предприятий с
численностью работников от 25 до
100 человек.
Астафурова И.С.
36. Значения параметров функции Лапласа для задачи:
1.Так как p=0,997, то t=32.Так как p=0,997, то t=2
Астафурова И.С.
37.
Рассчитаем выборочную среднюю и дисперсию поспособу моментов (ряд является интервальным рядом
распределения с равными интервалами), для этого
найдем условный ноль и шаг: A =62,5 (середина
интервала с максимальной частотой); h=25.
1
Группы по численности
работников, чел.
До
25
50
75
100
25
50
75
100
и выше
Итого:
Число
предприятий
xi
xi f i
x 2 i f i
15
20
35
25
5
100
-2
-1
0
1
2
-30
-20
0
25
5
-15
60
20
0
25
20
125
15
x
25 62,5 58,75
100
Астафурова И.С.
38.
27,70x 3
(1 0,05) 8,099
100
1. x =58,75; 27,6982;
8,099
50,651 ~x 66,849,
средняя численность работников
на предприятиях города от 50 до 67
человек;
2
x
x
Астафурова И.С.
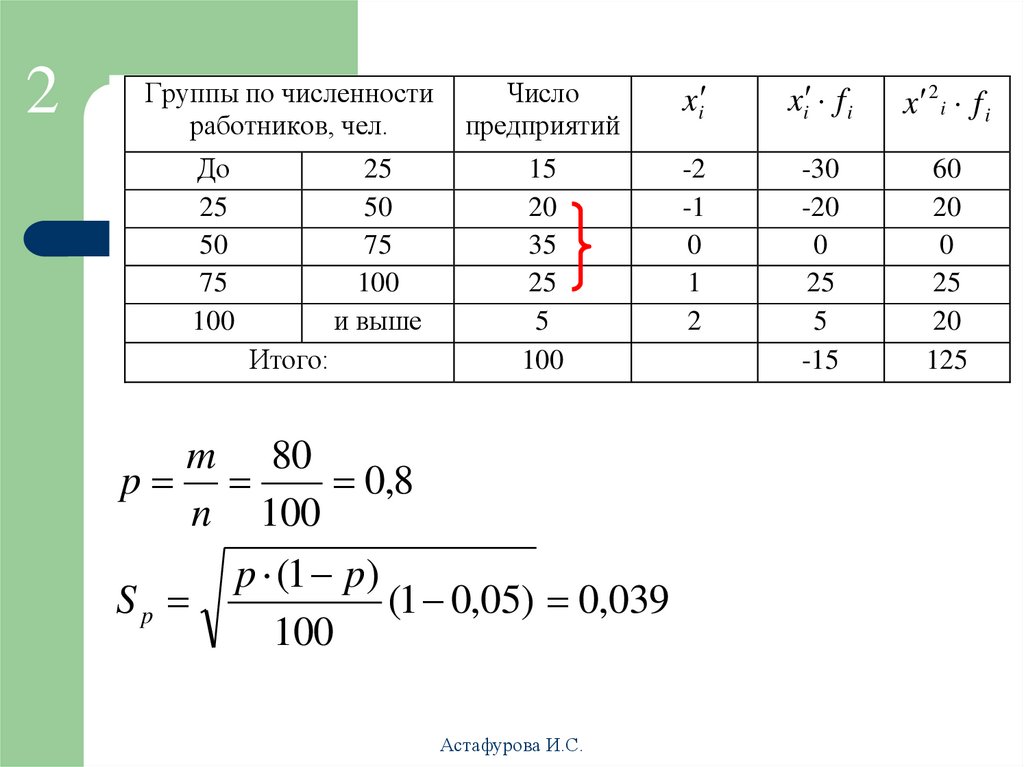
39.
2Группы по численности
работников, чел.
До
25
50
75
100
25
50
75
100
и выше
Итого:
Число
предприятий
xi
xi f i
x 2 i f i
15
20
35
25
5
100
-2
-1
0
1
2
-30
-20
0
25
5
-15
60
20
0
25
20
125
m 80
p
0,8
n 100
p (1 p)
Sp
(1 0,05) 0,039
100
Астафурова И.С.
40.
2Группы по численности
работников, чел.
До
25
50
75
100
25
50
75
100
и выше
Итого:
Число
предприятий
xi
xi f i
x 2 i f i
15
20
35
25
5
100
-2
-1
0
1
2
-30
-20
0
25
5
-15
60
20
0
25
20
125
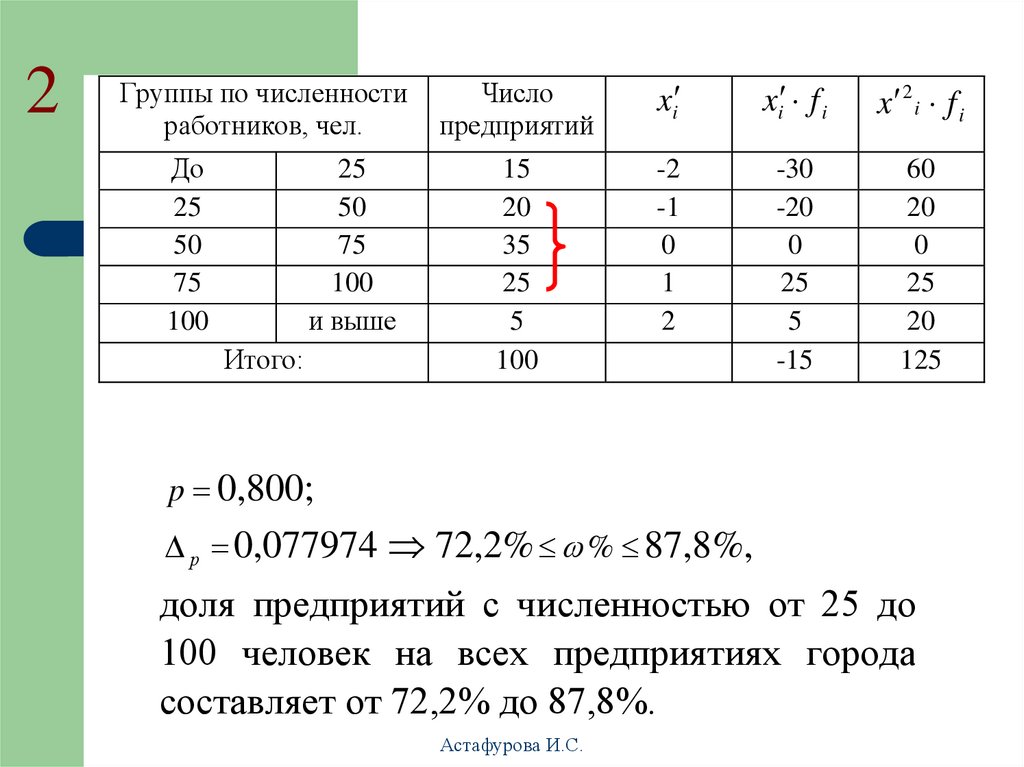
p 0,800;
р 0,077974 72,2% % 87,8%,
доля предприятий с численностью от 25 до
100 человек на всех предприятиях города
составляет от 72,2% до 87,8%.
Астафурова И.С.
41. САМОСТОЯТЕЛЬНО ИЗУЧИТЬ:
•ВИДЫ,•СПОСОБЫ
•МЕТОДЫ ОТБОРА
единиц совокупности из
генеральной в выборочную
Астафурова И.С.
42. ВЫВОДЫ:
1. Выборочное наблюдение, основанное наслучайном отборе, обеспечивает
репрезентативность отбора;
2. Основные причины проведения несплошного
наблюдения: экономия средств, сокращение
ошибок, необходимость детального изучения
единиц;
3. Только для выборочного наблюдения присущи
ошибки репрезентативности;
4. Формула для расчёта ошибки выборки зависит от
метода отбора.
Астафурова И.С.
43. ТЕМЫ на промежуточную аттестацию в среде тестирования СИТО:
1. Основные понятия и категориистатистики;
2. Сводка и группировка;
3. Абсолютные, относительные и
средние величины в статистике;
4. Меры вариации;
5. Выборочное наблюдение.
Астафурова И.С.
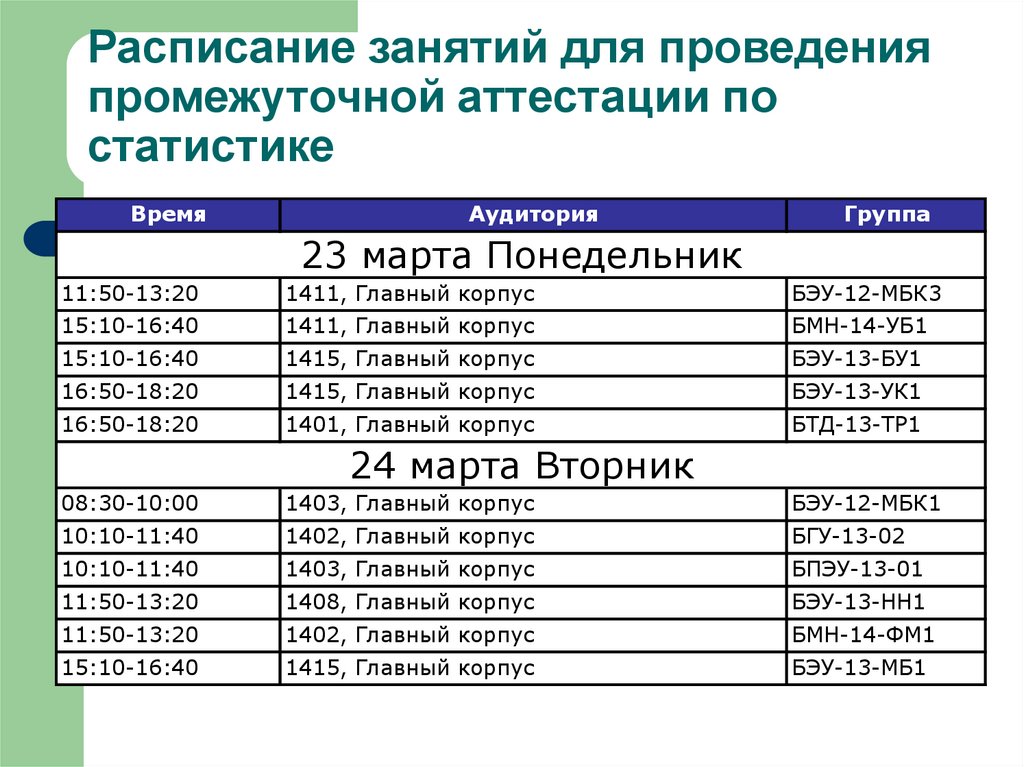
44. Расписание занятий для проведения промежуточной аттестации по статистике
ВремяАудитория
Группа
23 марта Понедельник
11:50-13:20
1411, Главный корпус
БЭУ-12-МБК3
15:10-16:40
1411, Главный корпус
БМН-14-УБ1
15:10-16:40
1415, Главный корпус
БЭУ-13-БУ1
16:50-18:20
1415, Главный корпус
БЭУ-13-УК1
16:50-18:20
1401, Главный корпус
БТД-13-ТР1
24 марта Вторник
08:30-10:00
1403, Главный корпус
БЭУ-12-МБК1
10:10-11:40
1402, Главный корпус
БГУ-13-02
10:10-11:40
1403, Главный корпус
БПЭУ-13-01
11:50-13:20
1408, Главный корпус
БЭУ-13-НН1
11:50-13:20
1402, Главный корпус
БМН-14-ФМ1
15:10-16:40
1415, Главный корпус
БЭУ-13-МБ1
45.
Расписание занятий для проведенияпромежуточной аттестации по
статистике
25 марта Среда
10:10-11:40
1408, Главный корпус
БПЭУ-13-02
10:10-11:40
1415, Главный корпус
БЭУ-13-МЭ1
11:50-13:20
1414, Главный корпус
БТД-13-ЛО2
11:50-13:20
1415, Главный корпус
БЭУ-13-МЭ2
26 марта Четверг
13:30-15:00
1405, Главный корпус
БЭУ-13-ФК2
16:50-18:20
1405, Главный корпус
БЭУ-13-ФК1
16:50-18:20
1415, Главный корпус
БЭУ-13-МП
27 марта Пятница
11:50-13:20
1401, Главный корпус
БЭУ-12-МБК4
11:50-13:20
13:30-15:00
1403, Главный корпус
1405, Главный корпус
БЭУ-13-МБ2
БМН-14/МТ/МС
13:30-15:00
1410, Главный корпус
БТД-13-ЛО1
15:10-16:40
1401, Главный корпус
БЭУ-12-ФКу/БУу
16:50-18:20
1408, Главный корпус
БТД-13-МА1
16:50-18:20
1414, Главный корпус
БЭУ-12-МБК2
46.
Астафурова И.С.47.
1Разница между значением показателя,
полученного по выборочной совокупности, и
генеральным параметром это (закончите
фразу):
1. среднее линейное отклонение;
2. колеблемость признака;
3. предельная ошибка выборки;
4. средняя ошибка выборки.
48.
2Чему равняется доля
единиц выборочной
совокупности,
обладающих изучаемым
свойством:
а) n/N;
б) m/n;
в) M/N;
г) p.
49.
3По какой формуле
рассчитывается предельная
ошибка выборочной средней
для бесповторного отбора?:
а)
б)
в)
г)
t*
t*
2
n
* (1
)
n
N
2
n
t*
p * (1 p )
n
t*
p * (1 p )
n
* (1
)
n
N
50.
92% 98%4
,
1.
2.
3.
4.
Сформулируйте фразу, описывающую
следующую цепочку неравенств:
92% 98% , если - удельный
вес предприятий, имеющих убыток.
Обследовано 100 предприятий региона,
а p=0.954:
от 92% до 98% предприятий региона имеют прибыль с
большой долей вероятности ;
от 92% до 98% предприятий региона имеют убыток как у
100 предприятий ;
от 92% до 98% предприятий региона имеют убыток с
вероятностью 0.954 ;
удельный вес 100 предприятий с вероятностью 0,954
определяет их границы в генеральной совокупности от 92
до 98% .
51.
5Выберите неверное
утверждение:
1. мода и медиана имеют ту же единицу
измерения, какую имеет изучаемый
признак;
2. ошибка выборки показывает отличие
генерального параметра от
выборочного;
3. если коэффициент вариации не
превышает 33%, то совокупность
является однородной;
4. предельная ошибка выборочной средней
имеет единицей измерения процент.
52. Коэффициент детерминации может принимать значения
6Коэффициент
детерминации может
принимать значения
1.
2.
3.
4.
от –1 до 1;
от 0 до 1;
–1 до 0;
любые положительные значения.
53.
7Межгрупповая дисперсия равна 81% от
общей дисперсии, эмпирическое
корреляционное отношение равно (с
точностью до 0,01)
1) 0,90;
2) 0,81;
3) 0,66;
4) 0,41.
54. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 100 изделий. В результате
8При проверке веса
импортируемого груза на таможне
методом случайной повторной
выборки было отобрано 100
изделий. В результате был
установлен средний вес изделия
40 г. при среднем квадратическом
отклонении 4 г. С вероятностью
0,997 определить предельную
ошибку выборки
55.
81)0,3;
2)1,2;
3)0,1;
4)0,399.
56.
9Какого вида, способа
или метода выборки
не существует?
1. индивидуальный;
2. групповой;
3. повторный;
4. комбинационный;
5. бесповторный;
6. серийный;
7. случайный.
57. Если параметр функции Лапласа увеличить с 2 до 3, то предельная ошибка :
10Если параметр функции Лапласа
увеличить с 2 до 3, то предельная
ошибка :
а) увеличится в 1,5 раза;
б) уменьшится в 1,5 раза;
в) не изменится
г) увеличится в 2 раза.




















































 mathematics
mathematics








