Цифровые измерительные приборы

1. Лекция № 7 Раздел 2. Цифровые измерительные приборы Тема 2.1. Преобразование аналоговой величины в дискретную 2.2.1. Общие

сведения о цифровых
электроизмерительных приборах и их
классификация
2.2.2. Дискретизация и квантование
2.2.3. Цифровое кодирование системы
счисления. Коды
2.2.4. Методы преобразования непрерывной
величины в дискретную

2. 2.2.1. Общие сведения о цифровых электроизмерительных приборах и их классификация

19
2.2.1. Общие сведения о цифровых
электроизмерительных приборах и их
классификация
Цифровой измерительный прибор (ЦИП) измерительный прибор, автоматически вырабатывающий дискретные сигналы измерительной
информации, показания которого представлены в
цифровой форме
Цифровые приборы являются автоматическими
приборами сравнения с непосредственным
отсчетом, работающие на принципе компенсации
измеряемой величины образцовой мерой
Результат измерения получается в момент
равенства измеряемой величин и образцовой
меры. Измеренное значение фиксируется счетным
устройством в цифровой форме на шкале прибора

3. Классификация цифровых измерительных приборов

18
Все цифровые приборы разделяются на две группы :
электромеханические
электронные.
В качестве образцовой меры, как правило, используется
напряжение или время.
По роду измеряемой величины ЦИП :
вольтметры, частотомеры, фазометры, омметры
комбинированные (мультиметры.).
В зависимости от степени усреднения значений измеряемой
величины ЦИП:
приборы, измеряющие мгновенное значение,
приборы, измеряющие среднее значение за определенный
интервал времени (интегрирующие).

4. Классификация цифровых измерительных приборов

По режиму работы :
приборы циклические (развертывающие или программные) весь процесс преобразования протекает всегда независимо от
значения измеряемой величины по заданной программе от
начала до конца
приборы следящие - процесс преобразования начинается
только при отклонении измеряемой величины от ранее
измеренного значения
Для построения электронных цифровых приборов
используются следующие методы непрерывно-дискретного
преобразования:
- метод последовательного счета (время- импульсный)
- метод поразрядного уравновешивания (кодоимпульсный)
- метод считывания
17

5. Принцип действия ЦИП

2.2.2. Дискретизация и квантование
16
Принцип действия ЦИП
Основан на преобразовании непрерывной
измеряемой величины в дискретный ряд ее
значений, закодированных в цифровой форме.
Этот процесс осуществляется с помощью аналогоцифрового преобразователя (АЦП), в котором сигнал
измерительной информации подвергается
дискретизации, квантованию и кодированию.
Дискретизация - процесс преобразования непрерывного
сигнала измерительной формации в дискретный.
Может осуществляться как по времени, так и по уровню.

6. Дискретизации по времени

2.2.2. Дискретизация и квантование
15
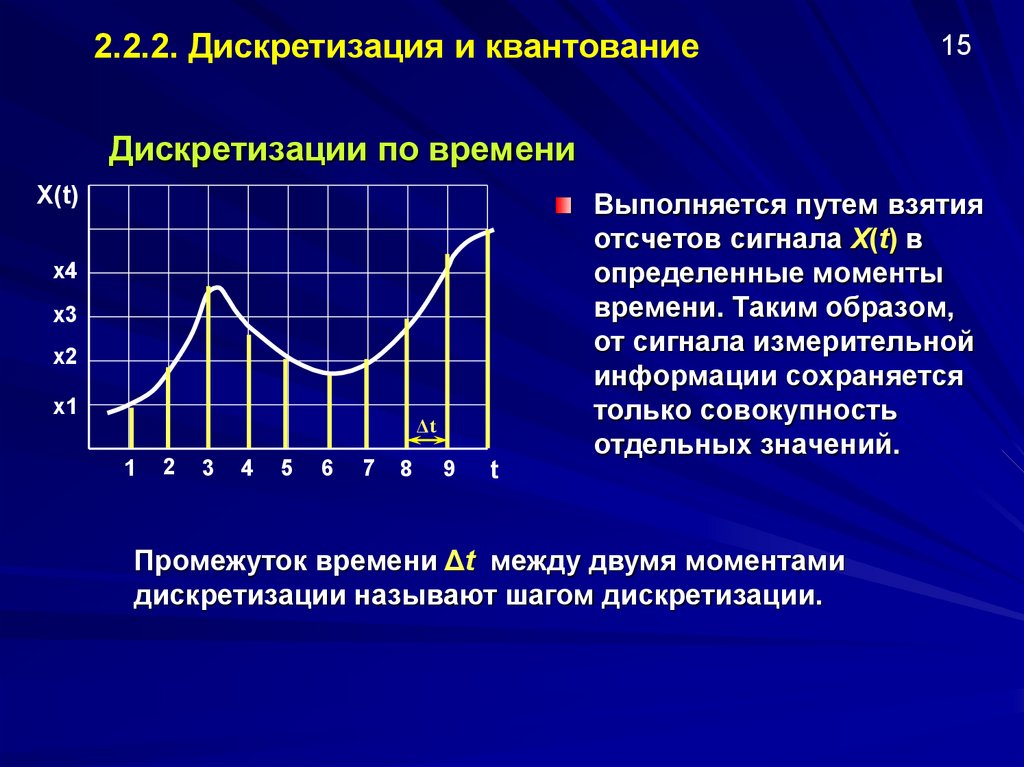
Дискретизации по времени
Х(t)
Выполняется путем взятия
отсчетов сигнала Х(t) в
определенные моменты
времени. Таким образом,
от сигнала измерительной
информации сохраняется
только совокупность
отдельных значений.
х4
х3
х2
х1
Δt
1
2
3
4
5
6
7
8
9
t
Промежуток времени Δt между двумя моментами
дискретизации называют шагом дискретизации.

7. Дискретизации по уровню

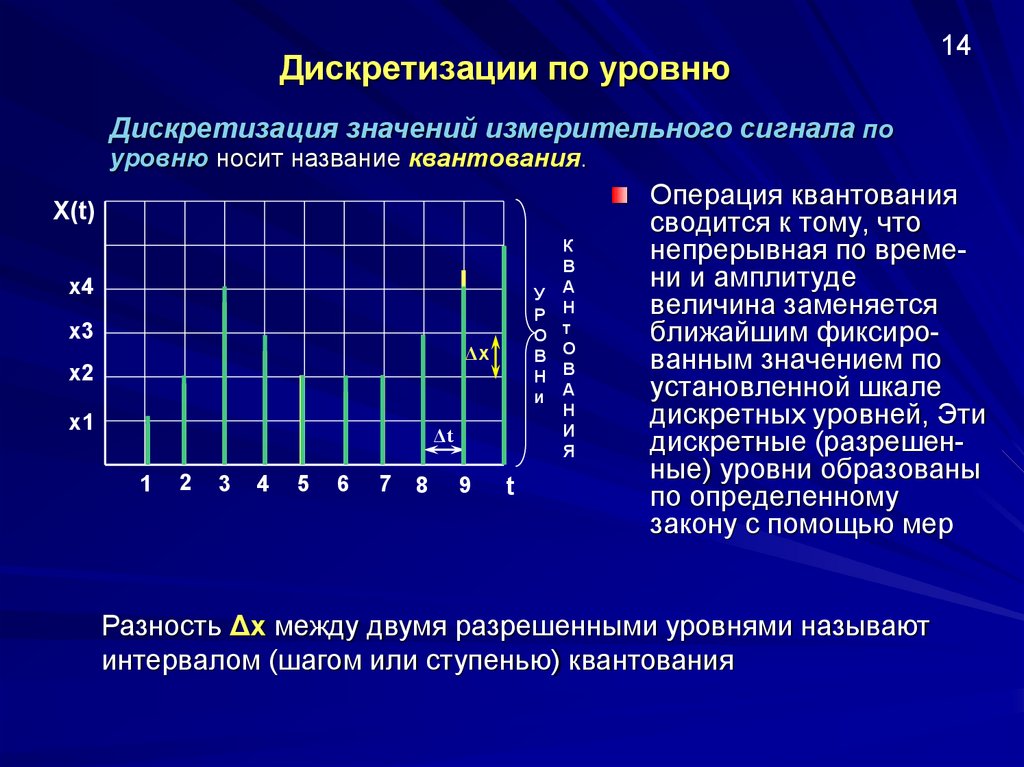
14
Дискретизация значений измерительного сигнала по
уровню носит название квантования.
Х(t)
К
В
У А
Р Н
О т
В О
Н В
и А
Н
И
Я
х4
х3
Δх
х2
х1
Δt
1
2
3
4
5
6
7
8
9
t
Операция квантования
сводится к тому, что
непрерывная по времени и амплитуде
величина заменяется
ближайшим фиксированным значением по
установленной шкале
дискретных уровней, Эти
дискретные (разрешенные) уровни образованы
по определенному
закону с помощью мер
Разность Δх между двумя разрешенными уровнями называют
интервалом (шагом или ступенью) квантования

8. Кодирование

13
Кодирование
Кодирование - представление численного значения
измеряемой величины последовательностью цифр или
сигналов, подчиняющихся определенному закону
Х(t)
К
В
У А
Р Н
О т
В О
Н В
и А
Н
И
Я
х4
х3
х2
х1
Х(ti)код
Δt
1
2
3
4
5
6
7
8
9
t
n1 n2 n3 n4 n5 n6 n7 n8 n9 n10 t
В ЦИП кодирование может быть
выполнено:
- числом импульсов
- числом одинаковых ступеней
образцового напряжения
- определённой комбинацией
различных по величине
образцовых напряжений
Наименьшей ступенью
дискретности в этих случаях
является или один импульс
или наименьшая величина
ступени напряжения.
При измерениях ЦИП
осуществляется замена
текущего значения
измеряемой величины
ближайшим дискретным
значением кода.
Число импульсов в кодовой группе прямо
пропорционально уровню квантованного сигнала

9. 2.2.3. Цифровое кодирование системы счисления. Коды

2.2.3. Цифровое кодирование системы счисления.12
Коды
Цифровой код представляет собой последовательность
цифр, подчиняющихся определенному закону, с помощью которого
условно отображают численное значение измеряемой величины.
В основе используемых цифровых кодов лежат различные
системы счисления
Системы счисления:
- десятичная;
- двоичная;
- двоично - десятичная
В ЦИП в основном применяют двоичную систему счисления , т.к.
для кодирования используются устройства с двумя устойчивыми
состояниями (триггеры). Результаты измерений во всех
измерительных приборах выражаются в десятичной системе. Для
перехода от двоичной системы к десятичной используется в
цифровых отсчетных устройствах двоично - десятичная система

10. 2.2.3. Цифровое кодирование системы счисления

11
2.2.3. Цифровое кодирование системы счисления
Система счисления основана на представлении любого числа в
виде суммы
К — коэффициент; Р — основание системы счисления; n — число
разрядов, в которое возводится основание системы счисления
Число 53 в двоичной системе счисления:
Для упрощения записи указывают только значения коэффициентов
К (0 или 1), располагая по убыванию номера разряда (слева
направо) — 110101.

11. 2.2.3. Цифровое кодирование системы счисления

10
2.2.3. Цифровое кодирование системы счисления
Код числа в двоичной системе счисления можно воспроизвести с
помощью электрических импульсов (сигналов). Считают, что
символу «1» соответствует наличие импульса (высокий уровень
сигнала), символу «0» — отсутствие импульса (низкий уровень
сигнала). Такой сигнал называется логическим и реализуется на
элементах, имеющих два устойчивых состояния (включен —
выключен; открыт — закрыт)
За уровень сигнала, соответствующий «1», можно принять
напряжение в интервале 2,4—5 В, а за уровень «0» — напряжение в
интервале 0—0,4 В.
Более значима длительность изменения уровня цифрового
сигнала. Цифровые логические устройства должны переходить из
одного состояния в другое без промежуточных состояний,
поэтому переход из уровня «1» в уровень «0» и обратно должен
происходить как можно быстрее. Длительность изменения уровня
цифрового сигнала определяется крутизной его фронтов, в
идеале сигнал должен иметь прямоугольную форму

12. 2.2.3. Цифровое кодирование системы счисления

9
2.2.3. Цифровое кодирование системы счисления
Переход от десятичных чисел к двоичным:
Номер разряда
(степень числа 2)
Десятичное число
0
1
1 2 3 4 5 6
7
8
9
10
2 4 8 16 32 64 128 256 512 1024
Перевод числа 53 в двоичную систему:
Действие
Результат
Остаток
53/2
26
1
26/2
13
0
13/2
6
1
6/2
3
0
3/2
1
1
В результате перевода десятичного числа 53 в двоичное (не
забывайте об обратном порядке) получим 110101,
т. е.
1 • 25 + 1 • 24 + 0 • 23 + 1 • 22 + 0 • 21 + 1 • 20 = 53.
1/2
0
1

13. 2.2.3. Цифровое кодирование системы счисления

8
2.2.3. Цифровое кодирование системы счисления
В десятичной системе счисления число 53 должно быть записано
следующим образом:
К = 0, 1, 2, ...,9.
Представление числа 53 в двоичном коде потребует 12 элементов
(6 — для символа «1» и 6 — для символа «0»), представление
числа в десятичном коде — 20 элементов. Двоичный код более
экономичный, чем десятичный, но управлять устройством,
отображающим информацию о результатах измерений в
десятичной системе счисления, более удобно

14. 2.2.3. Цифровое кодирование системы счисления

7
2.2.3. Цифровое кодирование системы счисления
Каждый сигнал в цифровой форме представляет собой
последовательность чисел. Каждое число состоит из N логических
сигналов, способных принимать значение 0 или 1. Эти сигналы
обозначают отдельные двоичные разряды числа, и, следовательно,
каждый логический сигнал несет ровно один бит информации. Вся
совокупность логических сигналов этого числа называется TV
логическим числом или информационным словом длиной N бит. В
зависимости от положения в двоичном числе каждый бит имеет
свое значение — вес. Так, вес крайнего правого бита 1 (единица);
второй (слева от первого) будет иметь вес 2; третий — 4 и т. д. (рис.
2, а).

15. 2.2.3. Цифровое кодирование системы счисления

6
2.2.3. Цифровое кодирование системы счисления
Двоичный код неудобен для управления десятичным отсчетным
устройством. Поэтому в ЦИП находит применение комбинация
систем счисления. Двоично-десятичная система по сложности и
экономичности занимает промежуточное положение между двумя
рассмотренными выше системами. Расположение десятичных
разрядов сохраняется, но цифра каждого десятичного разряда
изображается в двоичной системе.
Десятичные цифры 0—9 с «весами» 8—4—2—1 двоичного кода:
Десятичные
цифры
0
1
2
3
4
5
6
7
8
9
Код
8—4—2—1 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001

16. 2.2.3. Цифровое кодирование системы счисления

Число 53 в двоично-десятичной системе при «весах» элементов
двоичного кода 8—4—2—1 в каждом десятичном разряде
j — номер десятичного разряда,
5
3
0101 0011
5

17.

2.2.4. Методы преобразования непрерывной
величины в дискретную
4
Электронные ЦИП построены на принципе преобразования
измеряемой величины в пропорциональный интервал времени или
пропорциональную частоту.
Основным различием ЦИП по принципу построения
(принципу действия) является принцип или метод преобразования
непрерывной измеряемой величины в дискретную форму.
Для построения электронных цифровых приборов
используются следующие методы непрерывно-дискретного
преобразования:
- метод последовательного счета (время-импульсный);
- метод последовательного приближения (кодоимпульсный,
поразрядного уравновешивания) ;
- метод считывания.

18.

2.2.4. Методы преобразования непрерывной
величины в дискретную
3
Метод последовательного счета
Происходит последовательное во времени
сравнение измеряемой величины Х с
известной величиной Хк изменяющейся
(возрастающей или убывающей) во времени
скачками, причем каждый скачок
соответствует шагу (ступени) квантования по
уровню.
х
хк
tи
t
При некотором числе квантов n наступает
равенство (строгое или с некоторой
погрешностью nX0 = X , где Х - значений
измеряемой величины). Если вместо Х
использовать nX0 и выбрать Х0 равным
единице измерения Х, то число n будет
являться единичным кодом значения
измеряемой величины Х. Для получения
кода Х необходим последовательный счет
квантов Х0.

19. Метод последовательного приближения

2
Метод последовательного приближения
хк
tи
х
t
Происходит последовательное во времени
сравнение измеряемой величины Х с
известной величиной Хк изменяющейся во
времени скачками по определенному
алгоритму. Известная величина
воспроизводится набором мер, выбранных
по определенному правилу. Скачки зависят
от принятого набора мер.
Значение известной величины, при которой
наступает равенства
Хк(tи) = Х
соответствует номеру отождествляемого
уровня квантования, то есть
определенному набору мер. Код,
образуемый в процессе этой операции,
соответствует отождествляемому уровню

20. Метод считывания

х
tи
хкi+1
х
хкi
хк2
t
хк1
t
1
Происходит одновременное
сравнение измеряемой
величины X известными
величинами Xк1, Xк2,… Xкi
воспроизводимыми набором
мер, выбранных по
определенному правилу.
Известная величина, равная
измеряемой, дает номер
отождествляемого уровня
квантования.