Similar presentations:
Перпендикуляр и наклонная
1.
Перпендикуляр инаклонная
2.
Иллюстрациями какой теоремыможет быть картинка?
3.
Одно из красивейших произведений древнегреческойархитектуры – Парфенон (V в. до н. э.).
4.
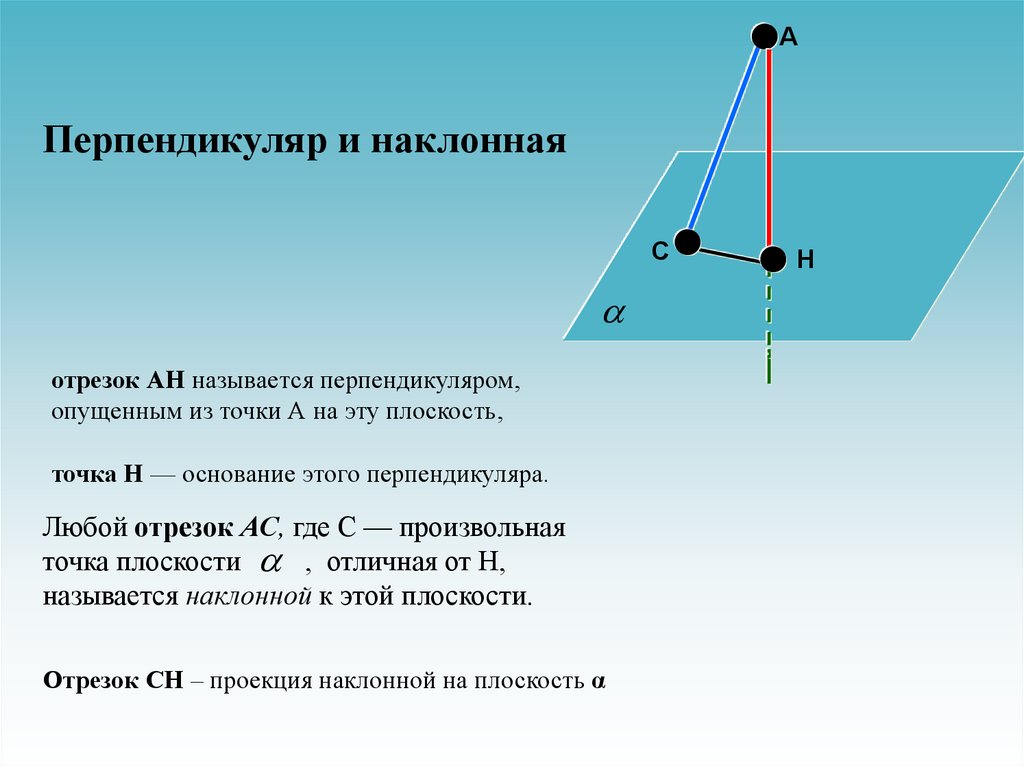
АПерпендикуляр и наклонная
С
отрезок АН называется перпендикуляром,
опущенным из точки А на эту плоскость,
точка Н — основание этого перпендикуляра.
Любой отрезок АС, где С — произвольная
точка плоскости , отличная от Н,
называется наклонной к этой плоскости.
Отрезок СН – проекция наклонной на плоскость α
Н
5.
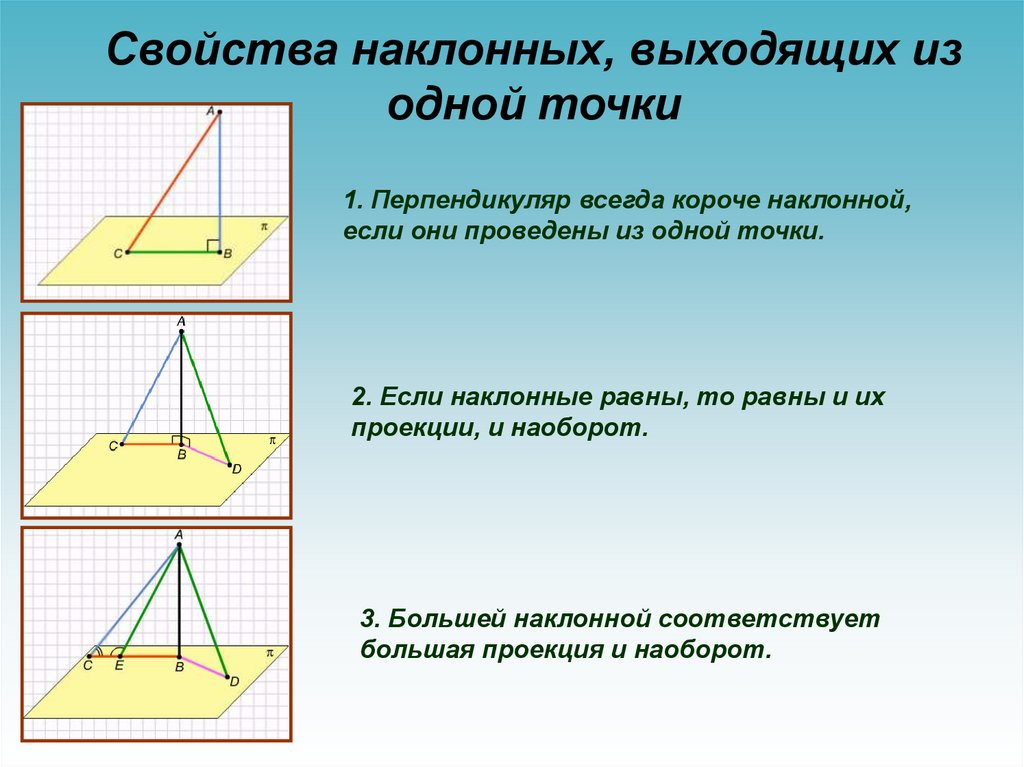
Свойства наклонных, выходящих изодной точки
1. Перпендикуляр всегда короче наклонной,
если они проведены из одной точки.
2. Если наклонные равны, то равны и их
проекции, и наоборот.
3. Большей наклонной соответствует
большая проекция и наоборот.
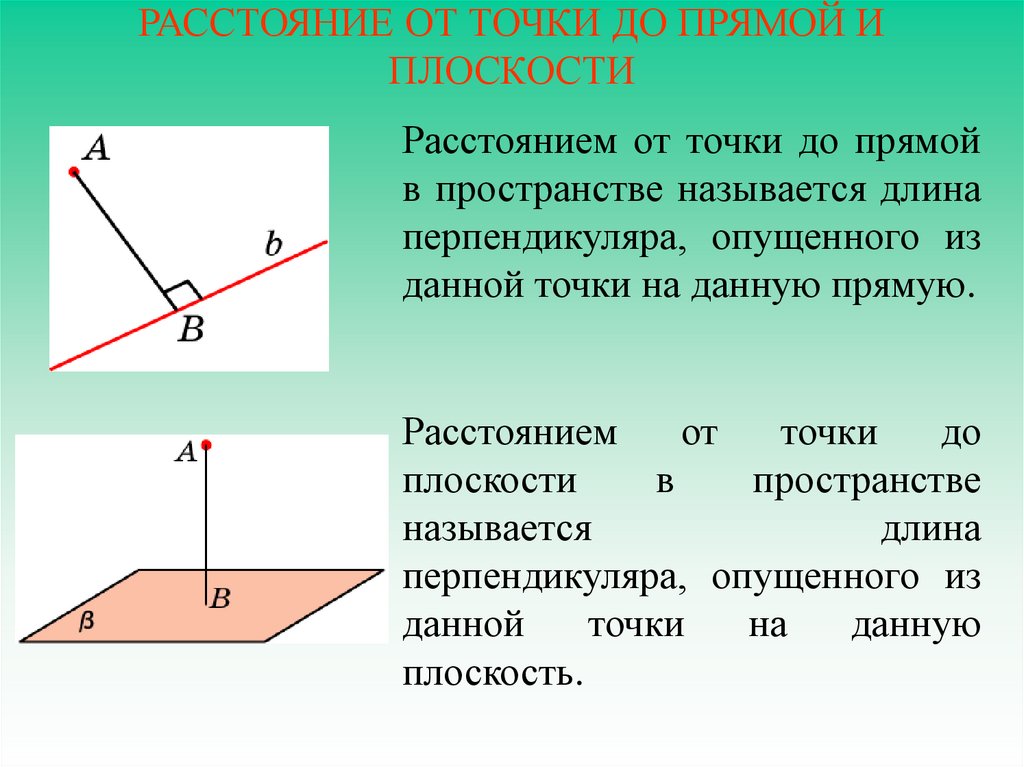
6. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ И ПЛОСКОСТИ
Расстоянием от точки до прямойв пространстве называется длина
перпендикуляра, опущенного из
данной точки на данную прямую.
Расстоянием
от
точки
до
плоскости
в
пространстве
называется
длина
перпендикуляра, опущенного из
данной
точки
на
данную
плоскость.
7.
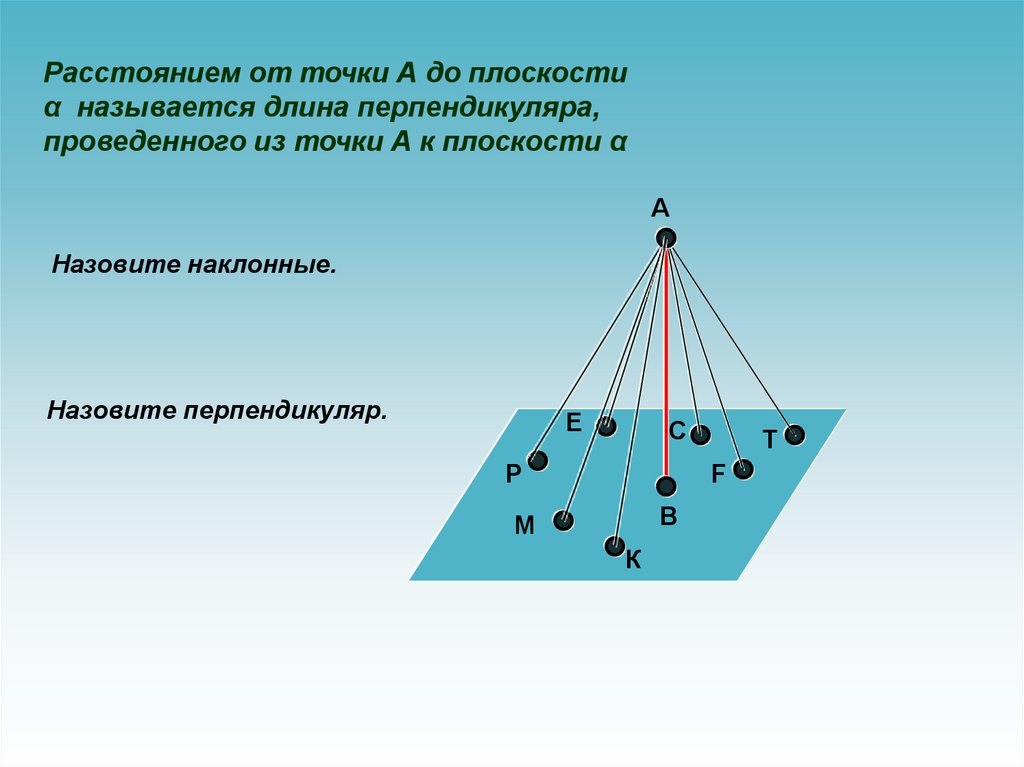
Расстоянием от точки А до плоскостиα называется длина перпендикуляра,
проведенного из точки А к плоскости α
А
Назовите наклонные.
Назовите перпендикуляр.
Е
С
Р
Т
F
В
М
К
8.
Расстояние между параллельными плоскостямиАА0 ; ВВ0 , тоАА0 || ВВ 0
А
α
В
β
А0
В0
АА0 ВВ0
Расстояние от произвольной точки
одной из параллельных плоскостей
до другой плоскости называется
расстоянием между
параллельными плоскостями.
9.
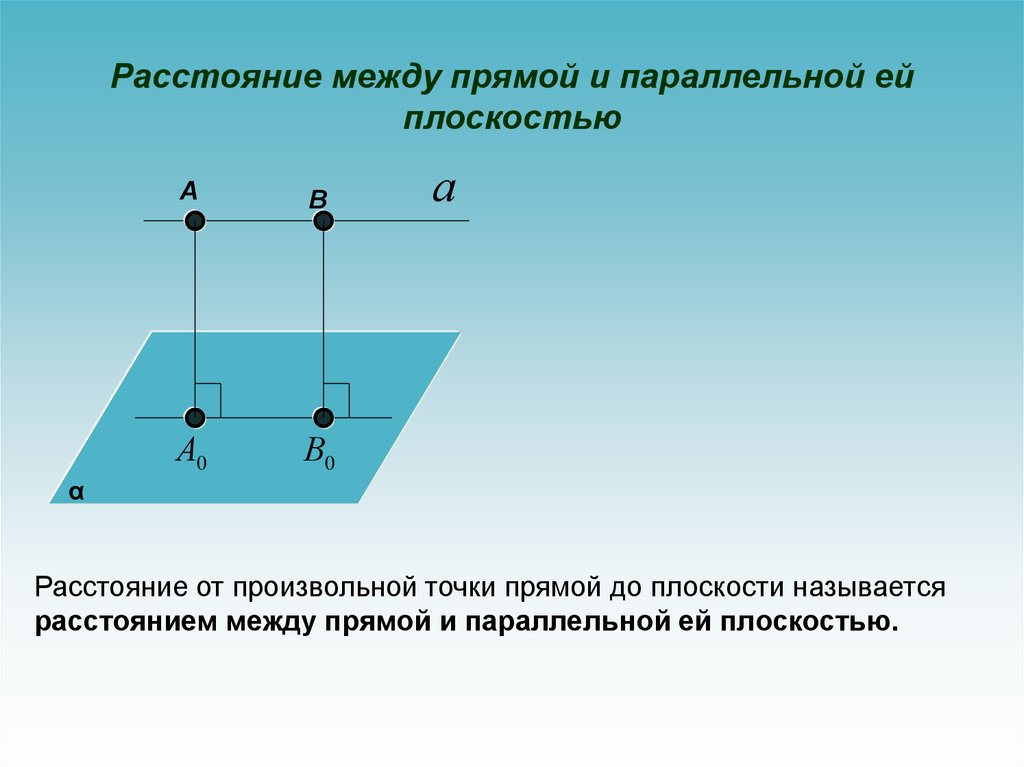
Расстояние между прямой и параллельной ейплоскостью
А
В
А0
В0
а
α
Расстояние от произвольной точки прямой до плоскости называется
расстоянием между прямой и параллельной ей плоскостью.
10.
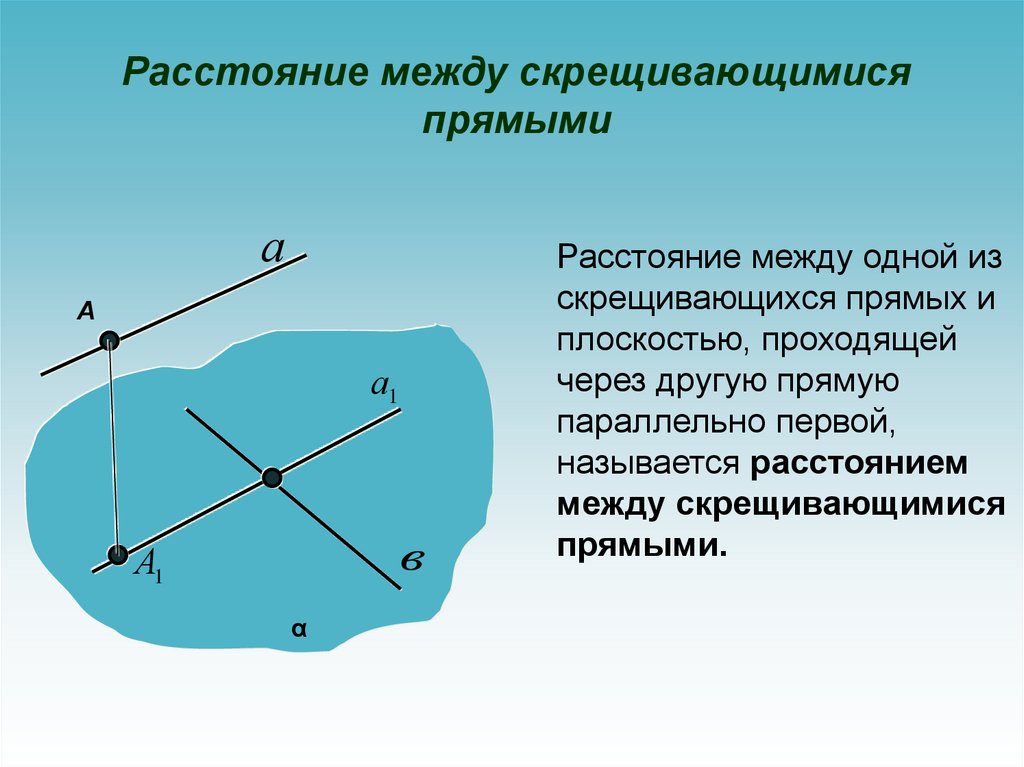
Расстояние между скрещивающимисяпрямыми
а
А
а1
в
А1
α
Расстояние между одной из
скрещивающихся прямых и
плоскостью, проходящей
через другую прямую
параллельно первой,
называется расстоянием
между скрещивающимися
прямыми.
11. Упражнение 1
К плоскости прямоугольника ABCD в точке пересечениядиагоналей восстановлен перпендикуляр. Верно ли утверждение
о том, что произвольная точка S этого перпендикуляра
равноудалена от вершин прямоугольника?
Дано :
SO ABCD ,
ABCD прямоуголь ник
Д - ть : AS BS CS DS
Ответ: Да.
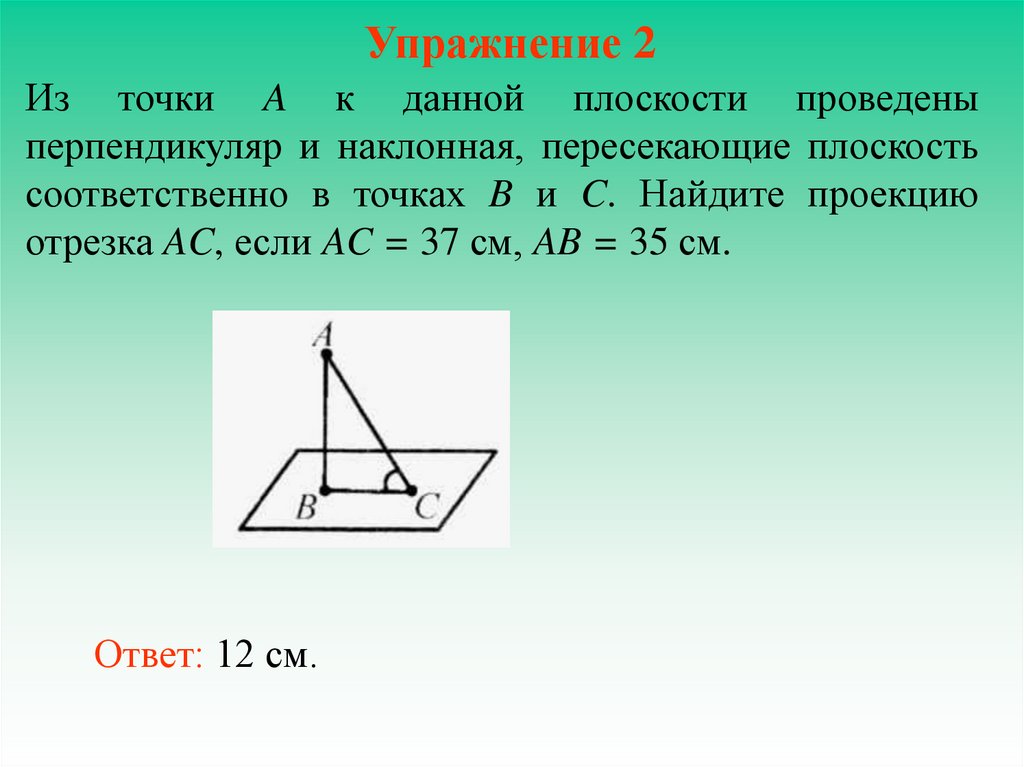
12. Упражнение 2
Из точки A к данной плоскости проведеныперпендикуляр и наклонная, пересекающие плоскость
соответственно в точках B и C. Найдите проекцию
отрезка AC, если AC = 37 см, AB = 35 см.
Ответ: 12 см.
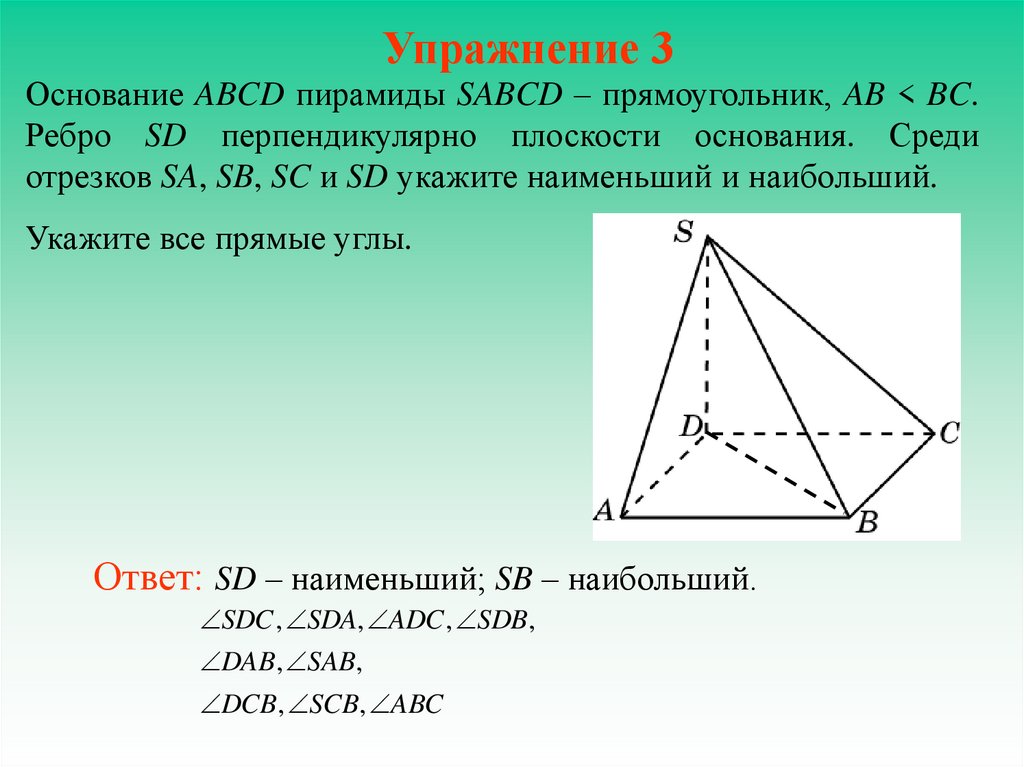
13. Упражнение 3
Основание ABCD пирамиды SABCD – прямоугольник, AB < BC.Ребро SD перпендикулярно плоскости основания. Среди
отрезков SA, SB, SC и SD укажите наименьший и наибольший.
Укажите все прямые углы.
Ответ: SD – наименьший; SB – наибольший.
SDC , SDA, ADC , SDB ,
DAB, SAB,
DCB, SCB, ABC





 mathematics
mathematics








