Similar presentations:
Решаем задачи №1-27 на синих слайдах
1.
ДЗ на 19.05.23г :Решаем задачи
№1-27 на синих
слайдах
2.
№1. Прототип задания 5 (№ 319353)Две фабрики выпускают одинаковые стекла для
автомобильных фар. Первая фабрика выпускает 45% этих
стекол, вторая – 55%. Первая фабрика выпускает 3%
бракованных стекол, а вторая – 1%. Найдите вероятность
того, что случайно купленное в магазине стекло окажется
бракованным.
x стёкол выпущено
I фабрика II фабрика
0,45 x
БРАК
0,55 x
P 0,0135 0,0055
0,03 0,45 x 0,01 0,55 x
0,45 0,03x 0,55 0,01x
P
x
Ответ : 0,019
3.
№1. Две фабрики выпускают одинаковые стекла дляавтомобильных фар. Первая фабрика выпускает 25% этих
стекол, вторая — 75%. Первая фабрика выпускает 4%
бракованных стекол, а вторая — 2%. Найдите вероятность
того, что случайно купленное в магазине стекло окажется
бракованным.
4.
№2. Прототип задания 5 (№ 319355)Если гроссмейстер А. играет белыми, то он выигрывает у
гроссмейстера Б. с вероятностью 0,52. Если А. играет
черными, то А. выигрывает у Б. с вероятностью 0,3.
Гроссмейстеры А. и Б. играют две партии, причем во второй
партии меняют цвет фигур. Найдите вероятность того, что А.
выиграет оба раза.
A(A. выигрывает белыми)
B(A. выигрывает чёрными)
P A B P A P B 0,52 0,3
Ответ : 0,156
5.
№2. Если шахматист А. играет белыми фигурами, то онвыигрывает у шахматиста Б. с вероятностью 0,56. Если А.
играет черными, то А. выигрывает у Б. с вероятностью 0,3.
Шахматисты А. и Б. играют две партии, причём во второй
партии меняют цвет фигур. Найдите вероятность того, что
А. выиграет оба раза.
6.
№3.Прототип задания 5 (№ 320171)
На экзамене по геометрии школьнику достаётся один вопрос
из списка экзаменационных вопросов. Вероятность того, что
это вопрос на тему «Вписанная окружность», равна 0,2.
Вероятность того, что это вопрос на тему «Параллелограмм»,
равна 0,15. Вопросов, которые одновременно относятся к этим
двум темам, нет. Найдите вероятность того, что на экзамене
школьнику достанется вопрос по одной из этих двух тем.
А- достанется вопрос на тему «Вписанная окружность»
В- достанется вопрос на тему «Параллелограмм»
А,В- несовместны
P A B P A P B
P A B 0,2 0,15
Ответ : 0,35
7.
№3. На экзамене по геометрии школьник отвечает на одинвопрос из списка экзаменационных вопросов. Вероятность
того, что это вопрос по теме «Вписанная окружность», равна
0,15. Вероятность того, что это вопрос по теме
«Тригонометрия»,
равна
0,3.
Вопросов,
которые
одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется
вопрос по одной из этих двух тем.
8.
№4. Прототип задания 5 (№ 320172)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что
к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе
закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу
дня кофе останется в обоих автоматах.
A(кофе останется в I автомате к концу дня)
B(кофе останется во II автомате к концу дня)
А,В – независимые события
P A P B 0,12
P A B 0,12
P A P B 0,12 0,7 0,7 1
P A P B 0,12 1,4 1
1 P A 1 P B 0,12
1 P A P B P A P B 0,12
P A P B 0,12 P A P B 1
Ответ : 0,52
9.
№4. В торговом центре два одинаковых автомата продаюткофе. Обслуживание автоматов происходит по вечерам после
закрытия центра. Известно, что вероятность события «К
вечеру в первом автомате закончится кофе» равна 0,25. Такая
же вероятность события «К вечеру во втором автомате
закончится кофе». Вероятность того, что кофе к вечеру
закончится в обоих автоматах, равна 0,15. Найдите
вероятность того, что к вечеру дня кофе останется в обоих
автоматах.
10.
№5. Прототип задания 5 (№ 320173)Биатлонист пять раз стреляет по мишеням. Вероятность
попадания в мишень при одном выстреле равна 0,8. Найдите
вероятность того, что биатлонист первые три раза попал в
мишени, а последние два промахнулся. Результат округлите
до сотых.
P 0,8 0,2
3
2
P 0,02048
Ответ : 0,02
11.
№5. Биатлонист три раза стреляет по мишеням. Вероятностьпопадания в мишень при одном выстреле равна 0,8. Найдите
вероятность того, что биатлонист первые три раза попал в
мишени, а последние два промахнулся. Результат округлите
до сотых.
12.
6. Прототип задания 5 (№ 320571)В магазине стоят два платёжных автомата. Каждый из них
может быть неисправен с вероятностью 0,05 независимо от
другого автомата. Найдите вероятность того, что хотя бы один
автомат исправен.
A(первый автомат исправен)
B(второй автомат исправен)
P 1 P A B
P 1 P A P B
P 1 0,0025
Ответ : 0,9975
13.
№6. В магазине стоят два платёжных автомата. Каждый изних может быть неисправен с вероятностью 0,06 независимо
от другого автомата. Найдите вероятность того, что хотя бы
один автомат исправен.
14.
7. Прототип задания 5 (№ 320175)Помещение освещается фонарём с двумя лампами.
Вероятность перегорания одной лампы в течение года равна
0,3. Найдите вероятность того, что в течение года хотя бы
одна лампа не перегорит.
A(первая лампа не перегорит в течение года)
В(вторая лампа не перегорит в течение года)
I способ
Ответ : 0,91
P A B A B A B
P 0,7 0,3 0,3 0,7 0,7 0,7
II способ
P 1 P A B 1 P A P B 1 0,09
15.
№7. Помещение освещается фонарём с двумя лампами.Вероятность перегорания одной лампы в течение года равна
0,13. Найдите вероятность того, что в течение года хотя бы
одна лампа не перегорит.
16.
№8. Прототип задания 5 (№ 320176)Вероятность того, что новый электрический чайник
прослужит больше года, равна 0,97. Вероятность того, что он
прослужит больше двух лет, равна 0,89. Найдите вероятность
того, что он прослужит меньше двух лет, но больше года.
A(чайник прослужит больше года)
В(чайник прослужит больше 2 лет)
A B B A
P A B P A P B
P A B 0,97 0,89 0,08
P A B P B P A
Ответ : 0,08
17.
№8. Вероятность того, что новый электрический чайникпрослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,87. Найдите вероятность
того, что он прослужит меньше двух лет, но больше года.
18.
№9. Прототип задания 5 (№ 320177)Агрофирма закупает куриные яйца в двух домашних
хозяйствах. 40% яиц из первого хозяйства – яйца высшей
категории, а из второго хозяйства – 20% яиц высшей
категории. Всего высшую категорию получает 35% яиц.
Найдите вероятность того, что яйцо, купленное у этой
агрофирмы, окажется из первого хозяйства.
x яиц закуплено в I хозяйстве
y яиц закуплено в II хозяйстве
0,4x 0,2 y 0,35 x y
x 3y
3y
P
y 3y
Ответ : 0,75
19.
№9. Агрофирма закупает куриные яйца в двух домашниххозяйствах. 85% яиц из первого хозяйства — яйца высшей
категории, а из второго хозяйства — 65% яиц высшей
категории. Всего высшую категорию получает 80% яиц.
Найдите вероятность того, что яйцо, купленное у этой
агрофирмы, окажется из первого хозяйства.
20.
№10. Прототип задания 5 (№ 320183)Перед началом футбольного матча судья бросает монетку,
чтобы определить, какая из команд начнёт игру с мячом.
Команда «Физик» играет три матча с разными командами.
Найдите вероятность того, что в этих играх «Физик»
выиграет жребий ровно два раза.
1
По формуле Бернулли P2 , 3 С
2
3
2
3
2
3
3
3!
3
C
P2,3
2! 8 8
2
Ответ : 0,375
21.
№10. Перед началом футбольного матча судья бросаетмонетку, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Сапфир» играет три матча с разными
командами. Найдите вероятность того, что в этих матчах
команда «Сапфир» начнёт игру с мячом не более одного раза.
22.
11. Прототип задания 5 (№ 320187)При артиллерийской стрельбе автоматическая система делает выстрел по цели.
Если цель не уничтожена, то система делает повторный выстрел. Выстрелы
повторяются до тех пор, пока цель не будет уничтожена. Вероятность
уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом
последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность
уничтожения цели была не менее 0,98?
i-м выстреле
Pi вероятность не поражения цели при
i 1
0,4 0,03 3
P1 1 0,4
3
0
,
4
0
,
064
0
,
03
3
P2 1 0,4 1 0,6
4
0,4 0,0256 0,03 3
i 1
Pi 1 0,4 1 0,6
P 1 0,6 0,4i 1 0,98
i 1
0,4 0,02 : 0,6
i 1 4
Ответ : 5
23.
№11. При артиллерийской стрельбе автоматическая система делает выстрел поцели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы
повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения
некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,5.
Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели
была не менее 0,95?
24.
№12. Прототип задания 5 (№ 320188Чтобы пройти в следующий круг соревнований, футбольной команде
нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает,
она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0
очков. Найдите вероятность того, что команде удастся выйти в
следующий круг соревнований. Считайте, что в каждой игре вероятности
выигрыша и проигрыша одинаковы и равны 0,4.
A(команда выигрывает игру )
В(команда играет вничью)
P A B B A A A
P 0,4 0,2 0,2 0,4 0,4 0,4 0,32
Ответ : 0,32
25.
№12. Чтобы пройти в следующий круг соревнований,футбольной команде нужно набрать хотя бы 7 очков в двух
играх. Если команда выигрывает, она получает 6 очков, в
случае ничьей — 1 очко, если проигрывает — 0 очков.
Найдите вероятность того, что команде удастся выйти в
следующий круг соревнований. Считайте, что в каждой игре
вероятности выигрыша и проигрыша одинаковы и равны 0,3.
26.
13. Прототип задания 5 (№ 320199)Чтобы поступить в институт на специальность «Лингвистика»,
абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх
предметов – математика, русский язык и иностранный язык. Чтобы
поступить на специальность «Коммерция», нужно набрать не менее 70
баллов по каждому из трёх предметов – математика, русский язык и
обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по
математике, равна 0,6, по русскому языку – 0,8, по иностранному языку –
0,7 и по обществознанию – 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из
двух упомянутых специальностей.
P P M P A P M P O P M P A O
P 0,6 0,8 0,7 0,6 0,8 0,5 0,6 0,8 0,7 0,5
Ответ : 0,408
27.
№13. Чтобы поступить в институт на специальность «Переводчик»,абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх
предметов – математика, русский язык и иностранный язык. Чтобы
поступить на специальность «Таможенное дело», нужно набрать не менее
79 баллов по каждому из трёх предметов – математика, русский язык и
обществознание.
Вероятность того, что абитуриент З. получит не менее 79 баллов по
математике, равна 0,9, по русскому языку – 0,7, по иностранному языку –
0,8 и по обществознанию – 0,9.
Найдите вероятность того, что Б. сможет поступить хотя бы на одну из
двух упомянутых специальностей.
28.
14. Прототип задания 5 (№ 320200)На фабрике керамической посуды 10% произведённых
тарелок имеют дефект. При контроле качества продукции
выявляется 80% дефектных тарелок. Остальные тарелки
поступают в продажу. Найдите вероятность того, что
случайно выбранная при покупке тарелка не имеет дефектов.
Ответ округлите до сотых.
x тарелок произведено
0,9 x
90
P
0,9 x 0,2 0,1x 92
Ответ : 0,978
29.
№14. На фабрике керамической посуды 20% произведённыхтарелок имеют дефект. При контроле качества продукции
выявляется 70% дефектных тарелок. Остальные тарелки
поступают в продажу. Найдите вероятность того, что
случайно выбранная при покупке тарелка не имеет дефектов.
Ответ округлите до сотых.
30.
№15. Прототип задания 5 (№ 320201)В магазине три продавца. Каждый из них занят с клиентом с
вероятностью 0,3. Найдите вероятность того, что в
случайный момент времени все три продавца заняты
одновременно (считайте, что клиенты заходят независимо
друг от друга).
A(I продавец занят )
B(II продавец занят )
C(III продавец занят )
P A B C P A P B P C 0,3
3
Ответ : 0,027
31.
№15. В магазине три продавца. Каждый из них занят склиентом с вероятностью 0,7. Найдите вероятность того, что в
случайный момент времени все три продавца заняты
одновременно (считайте, что клиенты заходят независимо
друг от друга).
32.
16. Прототип задания 5 (№ 320202)По отзывам покупателей Иван Иванович оценил надёжность двух
интернет-магазинов. Вероятность того, что нужный товар доставят из
магазина А, равна 0,8. Вероятность того, что этот товар доставят из
магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих
магазинах. Считая, что интернет-магазины работают независимо друг от
друга, найдите вероятность того, что ни один магазин не доставит товар.
A(товар доставят из магазина А )
В(товар доставят из магазина В )
P A B P A P B 0,1 0,2
Ответ : 0,02
33.
№16. По отзывам покупателей Иван Иванович оценил надёжность двухинтернет-магазинов. Вероятность того, что нужный товар доставят из
магазина А, равна 0,8. Вероятность того, что этот товар доставят из
магазина Б, равна 0,88. Иван Иванович заказал товар сразу в обоих
магазинах. Считая, что интернет-магазины работают независимо друг от
друга, найдите вероятность того, что ни один магазин не доставит товар.
34.
17. Прототип задания 5 (№ 320205)Перед началом футбольного матча капитаны команд тянут
честный жребий, чтобы определить, какая из команд начнёт
игру с мячом. Команда «Статор» по очереди играет с
командами «Ротор», «Мотор» и «Стартер». Найдите
вероятность того, что «Статор» будет начинать только
первую и последнюю игры.
1 1
P A 3
2
8
Ответ: 0,125
Ответ : 0,125
35.
№17. Перед началом футбольного матча капитаны командтянут честный жребий, чтобы определить, какая из команд
начнёт игру с мячом. Команда «Статор» по очереди играет с
командами «Ротор», «Мотор» и «Стартер». Найдите
вероятность того, что «Статор» будет начинать только
вторую и последнюю игры.
36.
18. Прототип задания 5 (№ 320207)Всем пациентам с подозрением на гепатит делают анализ крови. Если
анализ
выявляет гепатит,
то
результат анализа
называется
положительным. У больных гепатитом пациентов анализ даёт
положительный результат с вероятностью 0,9. Если пациент не болен
гепатитом, то анализ может дать ложный положительный результат с
вероятностью 0,01. Известно, что 5% пациентов, поступающих с
подозрением на гепатит, действительно больны гепатитом. Найдите
вероятность того, что результат анализа у пациента, поступившего в
клинику с подозрением на гепатит, будет положительным.
x пациентов обследуются
здоровы больны P 0,0095 x 0,045 x
0,95 x
Положительный
результат
0,05 x
0,01 0,95 x 0,9 0,05 x
x
Ответ : 0,0545
37.
№18. Всем пациентам с подозрением на гепатит делают анализ крови.Если анализ выявляет гепатит, то результат анализа называется
положительным. У больных гепатитом пациентов анализ даёт
положительный результат с вероятностью 0,9. Если пациент не болен
гепатитом, то анализ может дать ложный положительный результат с
вероятностью 0,02. Известно, что 77% пациентов, поступающих с
подозрением на гепатит, действительно больны гепатитом. Найдите
вероятность того, что результат анализа у пациента, поступившего в
клинику с подозрением на гепатит, будет положительным.
38.
19. Прототип задания 5 (№ 320210)Вероятность того, что батарейка бракованная, равна 0,06.
Покупатель в магазине выбирает случайную упаковку, в
которой две таких батарейки. Найдите вероятность того, что
обе батарейки окажутся исправными.
A(выбранная батарейка исправна)
A A C
2
независимые
события
P A 1 0,06 0,94
P C P A P A
P C 0,94 0,94
P C 0,8836
Ответ : 0,8836
39.
№19. Вероятность того, что батарейка бракованная, равна0,04. Покупатель в магазине выбирает случайную упаковку, в
которой две таких батарейки. Найдите вероятность того, что
обе батарейки окажутся исправными.
40.
20. Прототип задания 5 (№ 320211)Автоматическая
линия
изготавливает
батарейки.
Вероятность того, что готовая батарейка неисправна, равна
0,02. Перед упаковкой каждая батарейка проходит систему
контроля. Вероятность того, что система забракует
неисправную батарейку, равна 0,99. Вероятность того, что
система по ошибке забракует исправную батарейку, равна
0,01. Найдите вероятность того, что случайно выбранная
изготовленная батарейка будет забракована системой
контроля.
P 0,98 0,01 0,02 0,99
Ответ : 0,0296
41.
№20.Автоматическая линия изготавливает батарейки.
Вероятность того, что готовая батарейка неисправна, равна
0,01. Перед упаковкой каждая батарейка проходит систему
контроля. Вероятность того, что система забракует
неисправную батарейку, равна 0,95. Вероятность того, что
система по ошибке забракует исправную батарейку, равна 0,04.
Найдите вероятность того, что случайно выбранная
изготовленная батарейка будет забракована системой
контроля.
42.
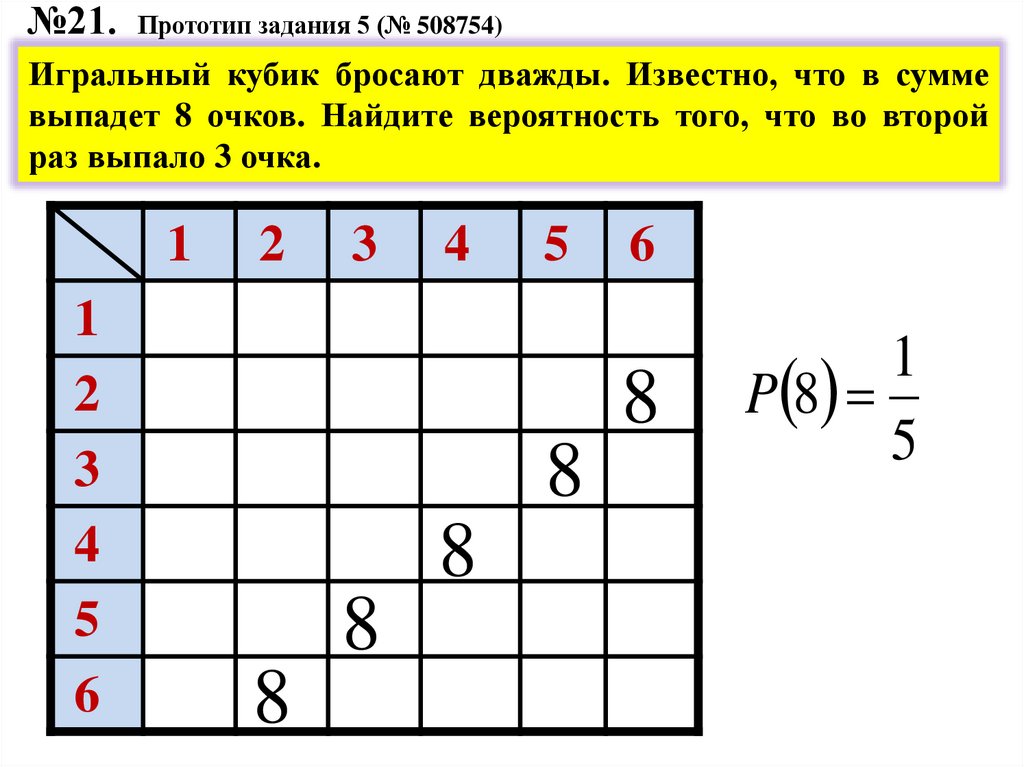
№21. Прототип задания 5 (№ 508754)Игральный кубик бросают дважды. Известно, что в сумме
выпадет 8 очков. Найдите вероятность того, что во второй
раз выпало 3 очка.
1
1
2
3
4
5
6
2
3
4
5
6
8
8
8
8
8
1
P 8
5
43.
№21. Игральный кубик бросают дважды. Известно, что всумме выпадет 9 очков. Найдите вероятность того, что во
второй раз выпало 5 очка.
44.
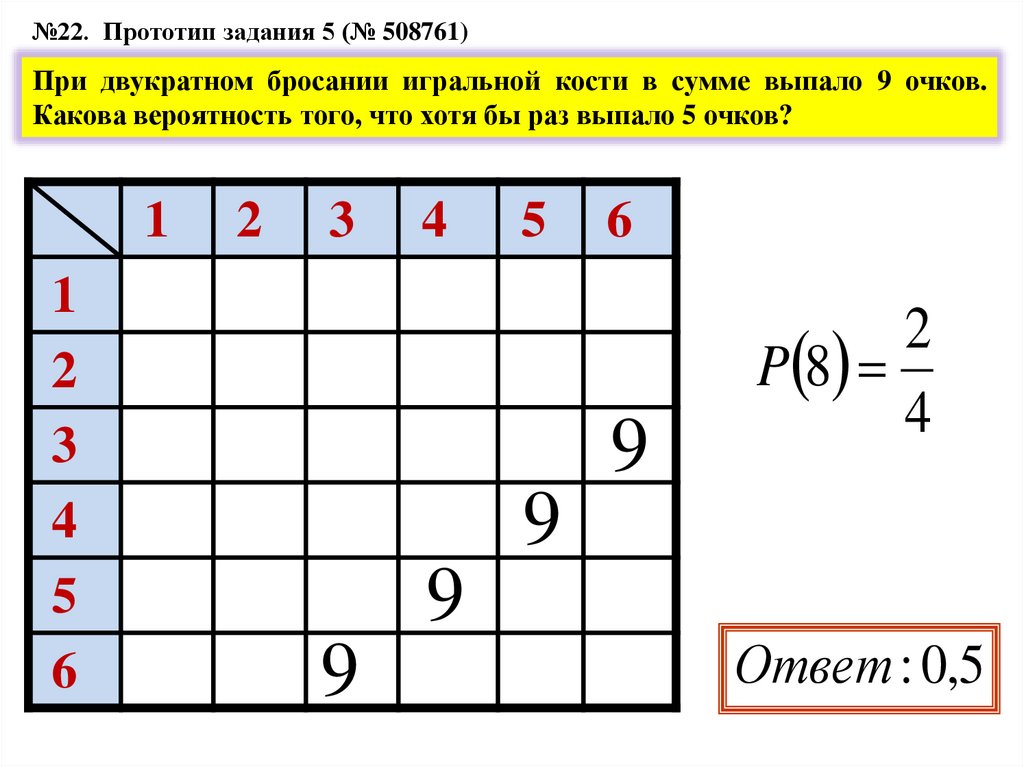
№22. Прототип задания 5 (№ 508761)При двукратном бросании игральной кости в сумме выпало 9 очков.
Какова вероятность того, что хотя бы раз выпало 5 очков?
1
1
2
3
4
5
6
2
3
4
5
6
9
2
P 8
4
9
9
9
Ответ : 0,5
45.
№22. При двукратном бросании игральной кости в сумме выпало 3 очка.Какова вероятность того, что хотя бы раз выпало 2 очка?
46.
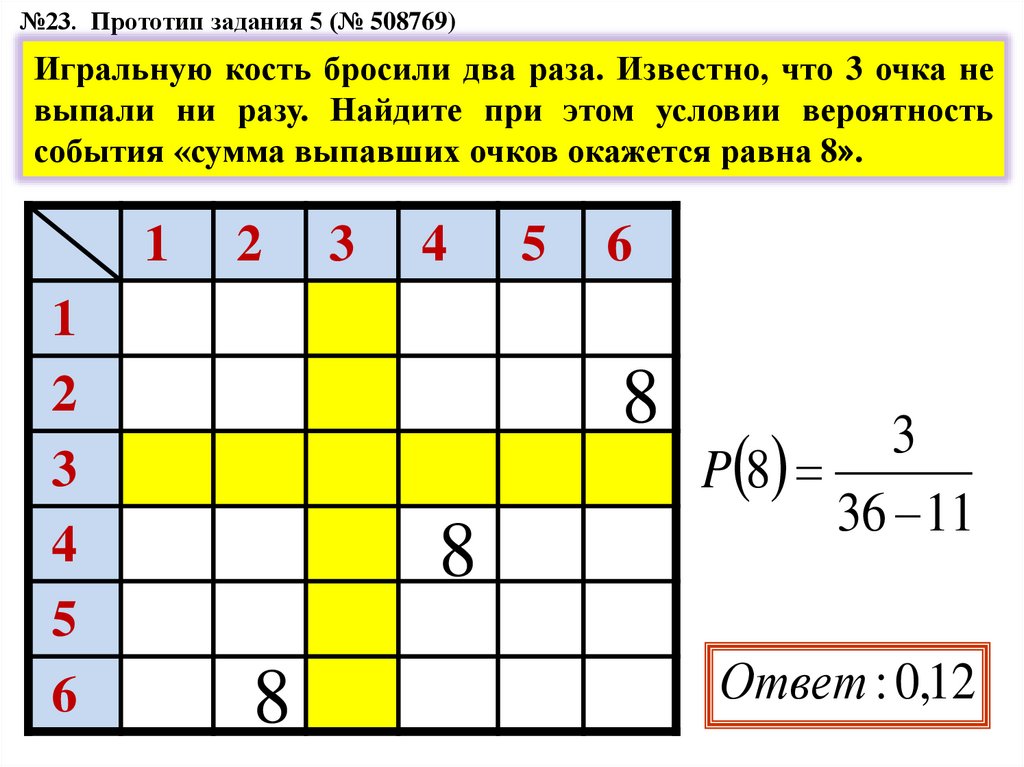
№23. Прототип задания 5 (№ 508769)Игральную кость бросили два раза. Известно, что 3 очка не
выпали ни разу. Найдите при этом условии вероятность
события «сумма выпавших очков окажется равна 8».
1
1
2
3
4
5
6
2
3
4
5
6
8
8
8
3
P 8
36 11
Ответ : 0,12
47.
№23. Игральную кость бросили два раза. Известно, что 6очков не выпали ни разу. Найдите при этом условии
вероятность события «сумма выпавших очков окажется
равна 5».
48.
24. Прототип задания 5 (№ 508780)Симметричную монету бросают 10 раз. Во сколько раз
вероятность события «выпадет ровно 5 орлов» больше
вероятности события «выпадет ровно 4 орла»?
10
10
10
10
10! 1
1
P5,10 С
5!5! 2
2
5
10
10! 1
1
P4,10 С
4!6! 2
2
4
10
10
1
10! 4! 6!
6
P5,10
2
10
P4,10
1
5
5! 5! 10!
2
Ответ: 1,2
49.
№24. Симметричную монету бросают 12 раз. Во сколько развероятность события «выпадет ровно 5 орлов» больше
вероятности события «выпадет ровно 4 орла»?
50.
25. Прототип задания (№ 508791)В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в
«Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит
комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит
комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность
получить комплимент? Результат округлите до сотых.
Вероятность выбросить комбинацию 5 и 6 очков
складывается из двух несовместных событий: на
первом кубике выпало 5 очков, а на втором кубике
выпало 6 очков или на первом кубике выпало 6
очков, а на втором кубике выпало 5 очков.
Вероятность
противоположного
события,
состоящего в том, что при одном броске костей
комбинация 5 и 6 очков не выпадет, равна
1 1 1 1 1
p
6 6 6 6 18
Вероятность того, что при двух бросках игральных
костей комбинация 5 и 6 очков не выпадет ни разу, равна
Вероятность
противоположного
события,
состоящего в том, что при двух бросаниях
игральных костей комбинация 5 и 6 очков
выпадет хотя бы один раз, равна
1 17
18 18
17 17 289
18 18 324
q 1 p 1
289
35
1
0,108
324 324
Ответ : 0,11
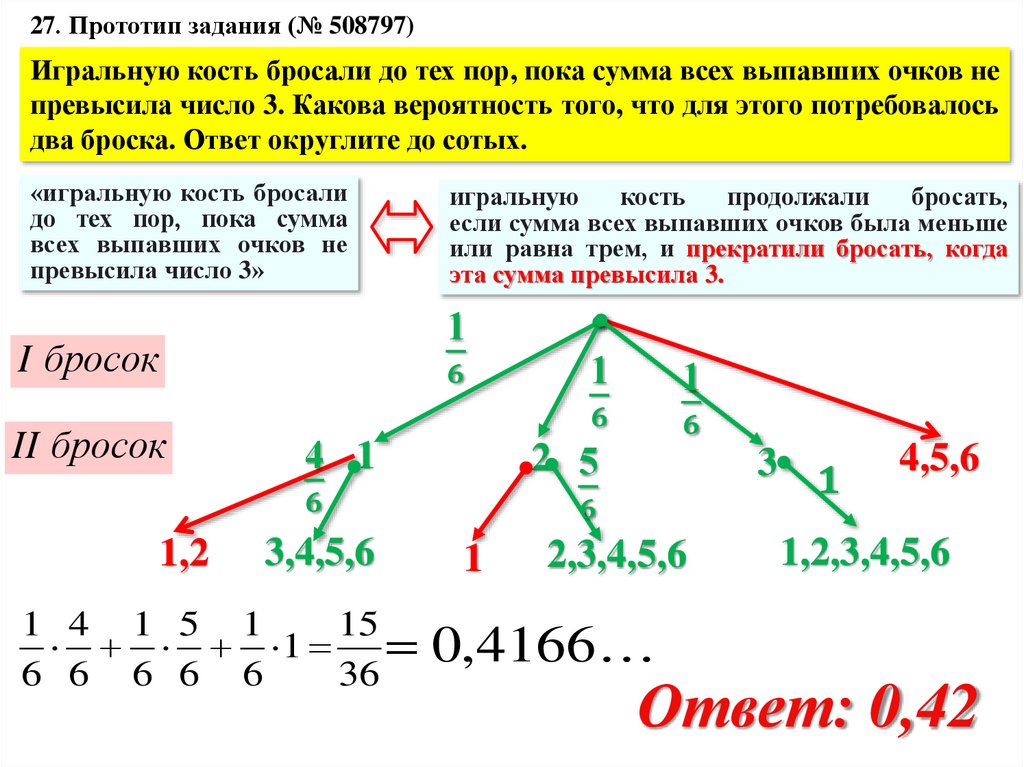
51.
№26 (№508792)Игральную кость бросили один или несколько раз. Оказалось,
что сумма всех выпавших очков равна 4. Какова вероятность
того, что был сделан один бросок? Ответ округлите до сотых.
A (сумма выпавших очков равна 4)
B (был сделан 1 бросок)
P A B P A P B / A 1
1
1 1
P A B



















































 mathematics
mathematics








