Системы счисления

1.

Теоретический материал
Системы счисления
Доцент кафедры АЭМИС
к.т.н. Кечкина Наталия Игоревна

2.

Основные определения и понятия
Система счисления — это правила записи чисел с
помощью специальных знаков — цифр, а также
соответствующие правила выполнения операций с
этими числами.
Позиционная система: значение цифры определяется
ее позицией в записи числа.
Алфавит системы счисления — это используемый в
ней набор цифр.
Основание системы счисления — это количество
цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды
в записи целых чисел нумеруются с нуля справа
налево.
2

3.

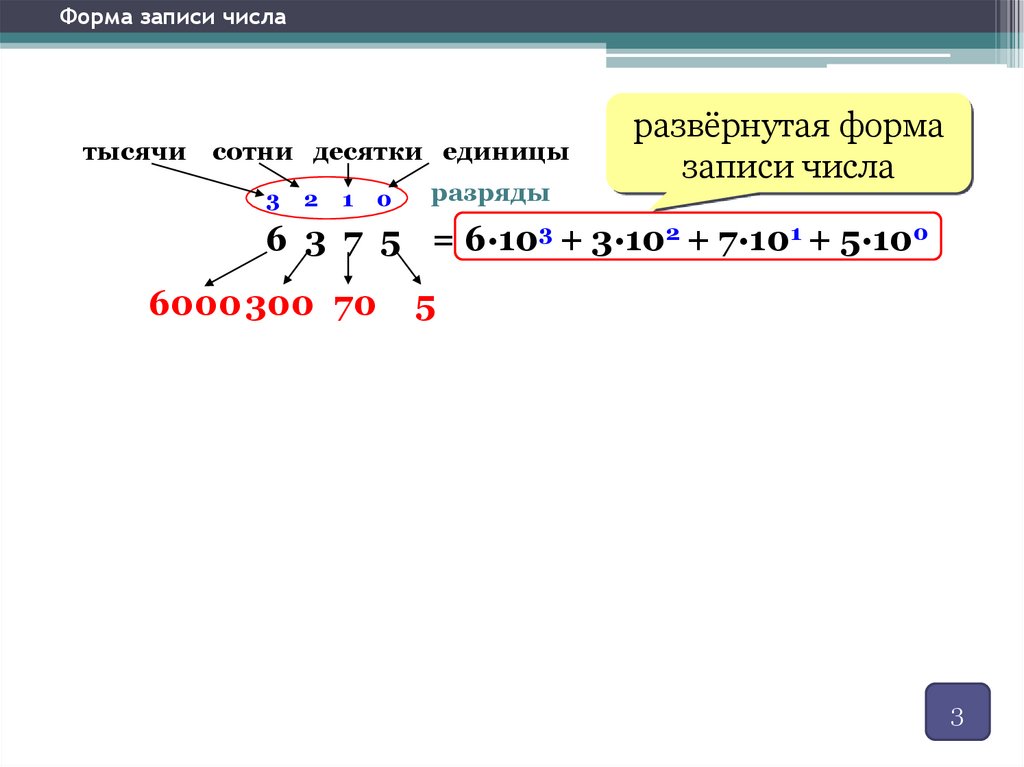
Форма записи числа
тысячи
сотни десятки единицы
3
2
1
0
разряды
развёрнутая форма
записи числа
6 3 7 5 = 6·103 + 3·102 + 7·101 + 5·100
6000 300 70
5
3

4.

Перевод из любой позиционной системы счисления в десятичную систему
Через развёрнутую запись числа:
разряды: 3 2 1 0
a3a2a1a0 = a3 p 3 + a2 p 2 + a1 p 1 + a0 p 0
=1
разряды: 3 2 1 0
12345 = 1 53 + 2 52 + 3 51 + 4 50 = 194
основание системы счисления
4

5.

Перевод из любой позиционной системы счисления в десятичную систему
Через развёрнутую запись числа:
разряды: -1 -2 -3 -4
0,a1 a2 a3 a4p = a1 p -1 + a2 p -2 + a3 p -3 + a4 p -4
разряды: -1 -2 -3 -4
0, 1 2 3 45 = 1·5-1 + 2·5-2 + 3·5-3 + 4·5-4
перевод в десятичную систему
5

6.

Перевод из десятичной системы счисления в любую позиционную систему
Делим число на основание новой позиционной
системы счисления p, отбрасывая остаток
на каждом шаге до тех пор, пока не получится
0. Затем необходимо выписать найденные
остатки в обратном порядке.
10 5
194 5
190 38 5
4 35 7
3 5
2
194 = 12345
5
1
0
5
0
1
6

7.

Перевод из десятичной системы счисления в любую позиционную систему
10 5
0,9376
Вычисления
Целая часть
Дробная часть
0,9376 5 = 4,688
0,688 5 = 3,44
0,44 5 = 2,2
0,2 5 = 1
4
3
2
1
0,688
0,44
0,2
0
0,9376 = 0,43215
7

8.

Перевод из двоичной в восьмеричную
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
Ответ:
1
3
5
7
10010111011112 = 113578
8

9.

Перевод из двоичной в шестнадцатеричную
10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ:
10010111011112 = 12EF16
9

10.

Арифметические операции
сложение
вычитание
0+0=0 0+1=1перенос0-0=0 1-1=0
1+0=1 1+1=102
1-0=1 102-1=1
заём
1 + 1 + 1 = 112
11111
1 0 1 1 02
+ 1 1 1 0 1 12
1 0 1 0 0 0 12
0 1 1 102 0 102
1 0 0 0 1 0 12
–
1 1 0 1 12
0 1 0 1 0 1 02
10

11.

Арифметические операции
умножение
1 0 1 0 12
1 0 12
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
деление
1 0 1 0 12 1 1 12
– 1 1 12
1 12
1 1 12
– 1 1 12
0
11

12.

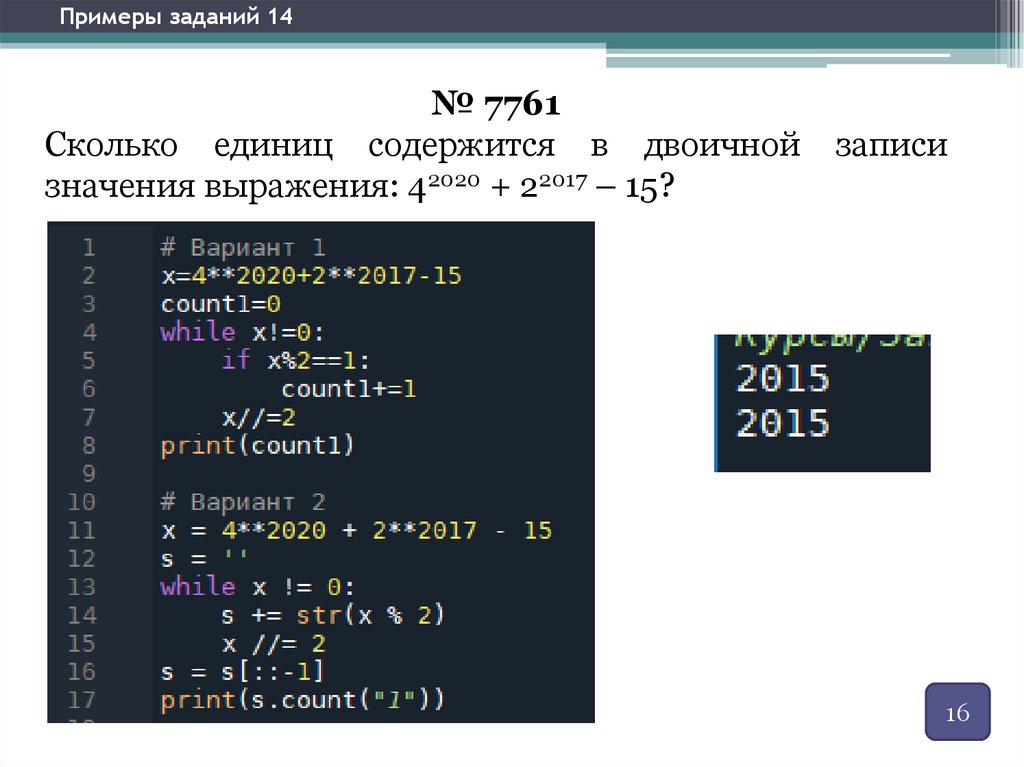
Примеры заданий 14
№ 7761
Сколько единиц содержится в двоичной
значения выражения: 42020 + 22017 – 15?
записи
Полезные свойства:
10N = 10…010
N
10N – 1= 9…910
N
10N – 10M = 10M (10N-M – 1) = 9…90…010
N–M M
12

13.

Примеры заданий 14
№ 7761
Сколько единиц содержится в двоичной
значения выражения: 42020 + 22017 – 15?
записи
42020 + 22017 – 15= 24040 + 22017 – 16+1= 24040 + 22017 – 24+20
24040 = 100…0002
4040
22017 =100…0002
2017
2+2022+2017=4041
24040 + 22017 = 100…00100…0000002
4040-2017-1=
=2022
2017
13

14.

Примеры заданий 14
№ 7761
Сколько единиц содержится в двоичной
значения выражения: 42020 + 22017 – 15?
записи
42020 + 22017 – 15= 24040 + 22017 – 16+1= 24040 + 22017 – 24+20
24040 + 22017 - 24 = 100…00100…0000002 - 100002 =
4041
=100…00011…1100002
2022+1=
=2023
4
2017-4=
=2013
14

15.

Примеры заданий 14
№ 7761
Сколько единиц содержится в двоичной
значения выражения: 42020 + 22017 – 15?
записи
42020 + 22017 – 15= 24040 + 22017 – 16+1= 24040 + 22017 – 24+20
24040 + 22017 - 24 + 20= 100…00011…1100002 + 102 =
4041
= 100…00011…1100102
2022+1=
=2023
2
1
2017-4=
=2013
Количество единиц 1+2013+1=2015
15

16.

Примеры заданий 14
№ 7761
Сколько единиц содержится в двоичной
значения выражения: 42020 + 22017 – 15?
записи
16

17.

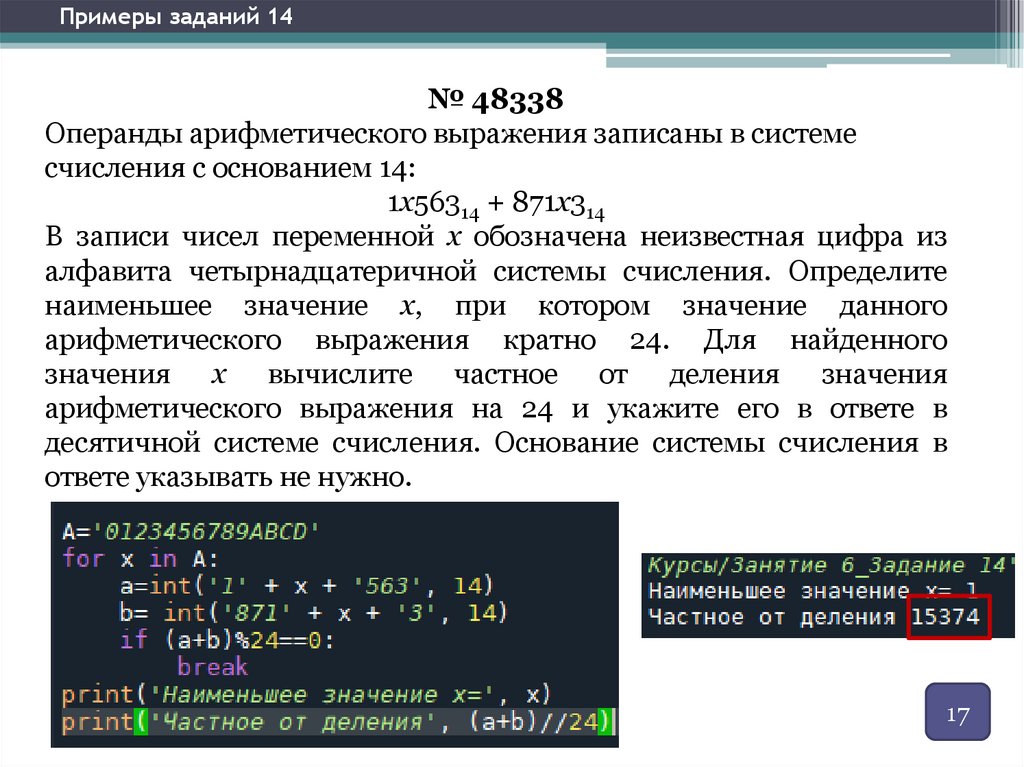
Примеры заданий 14
№ 48338
Операнды арифметического выражения записаны в системе
счисления с основанием 14:
1x56314 + 871x314
В записи чисел переменной x обозначена неизвестная цифра из
алфавита четырнадцатеричной системы счисления. Определите
наименьшее значение x, при котором значение данного
арифметического выражения кратно 24. Для найденного
значения x вычислите частное от деления значения
арифметического выражения на 24 и укажите его в ответе в
десятичной системе счисления. Основание системы счисления в
ответе указывать не нужно.
17

18.

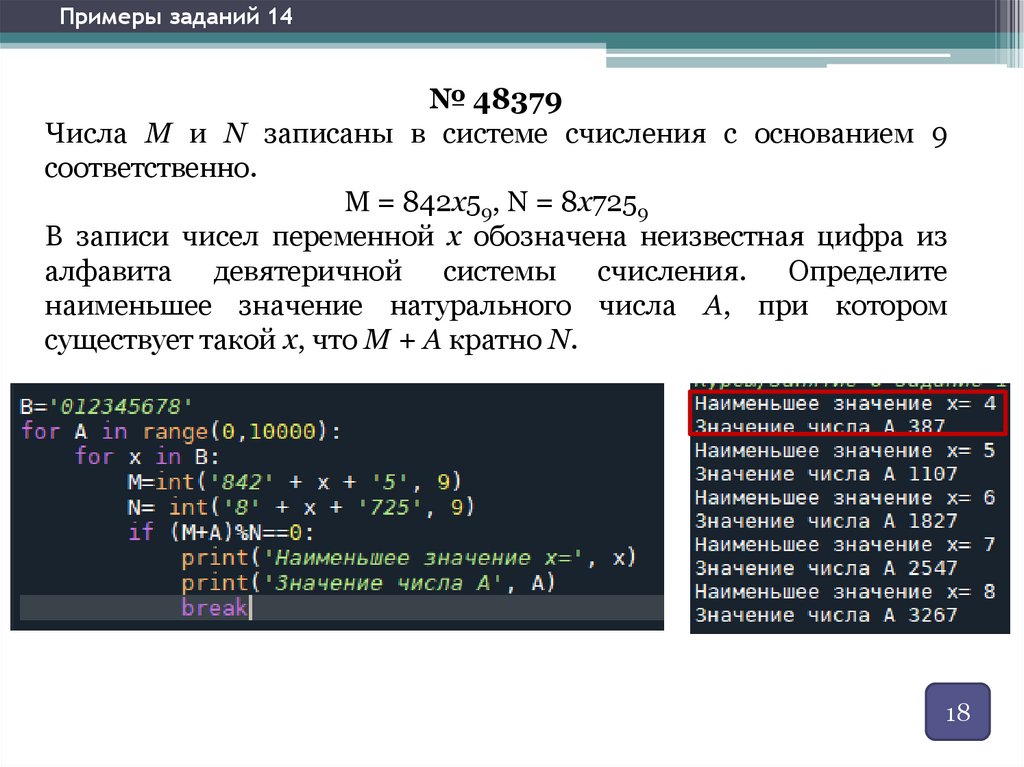
Примеры заданий 14
№ 48379
Числа M и N записаны в системе счисления с основанием 9
соответственно.
M = 842x59, N = 8x7259
В записи чисел переменной x обозначена неизвестная цифра из
алфавита девятеричной системы счисления. Определите
наименьшее значение натурального числа A, при котором
существует такой x, что M + A кратно N.
18

19.

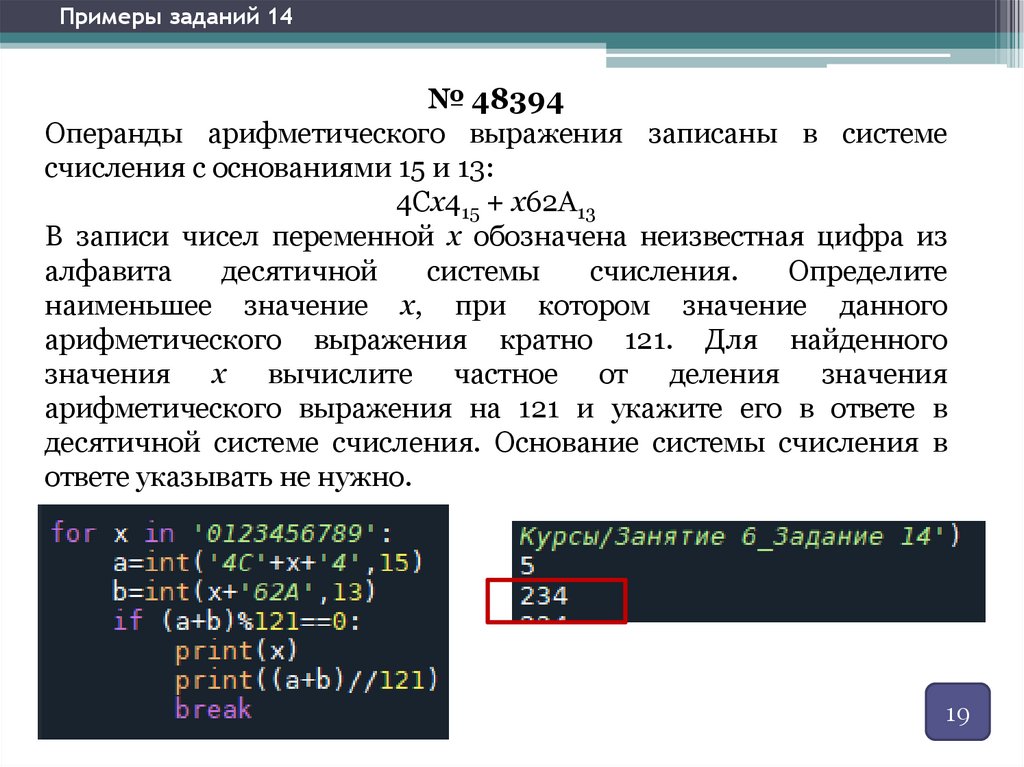
Примеры заданий 14
№ 48394
Операнды арифметического выражения записаны в системе
счисления с основаниями 15 и 13:
4Cx415 + x62A13
В записи чисел переменной x обозначена неизвестная цифра из
алфавита
десятичной
системы
счисления.
Определите
наименьшее значение x, при котором значение данного
арифметического выражения кратно 121. Для найденного
значения x вычислите частное от деления значения
арифметического выражения на 121 и укажите его в ответе в
десятичной системе счисления. Основание системы счисления в
ответе указывать не нужно.
19

20.

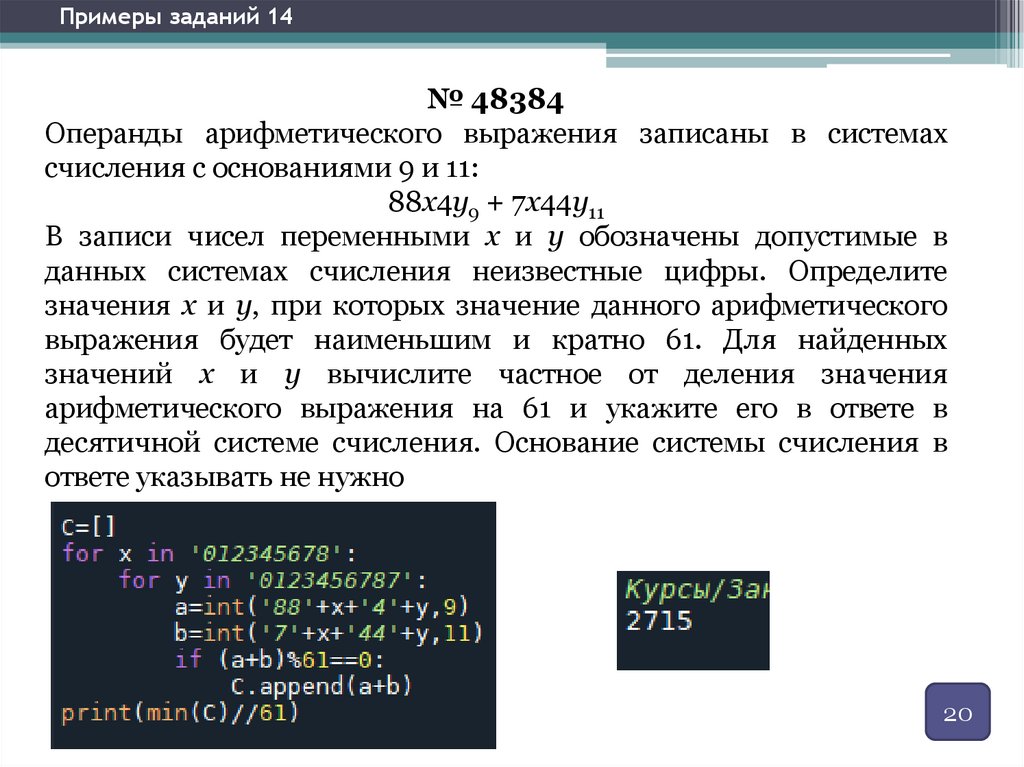
Примеры заданий 14
№ 48384
Операнды арифметического выражения записаны в системах
счисления с основаниями 9 и 11:
88x4y9 + 7x44y11
В записи чисел переменными x и y обозначены допустимые в
данных системах счисления неизвестные цифры. Определите
значения x и y, при которых значение данного арифметического
выражения будет наименьшим и кратно 61. Для найденных
значений x и y вычислите частное от деления значения
арифметического выражения на 61 и укажите его в ответе в
десятичной системе счисления. Основание системы счисления в
ответе указывать не нужно
20