Задача на оптимизацию. Задача №17

1.

ЗАДАЧА №17
Задача на оптимизацию

2. Методы решения задач на оптимизацию:

• метод перебора вариантов
• метод логических рассуждений (составление уравнения)
• метод исследования функции

3.

Основные этапы решения текстовой задачи:
подробный разбор условия задачи для четкого понимания сути описанного
в задаче процесса;
выбор переменных;
составление уравнения или неравенства, систем уравнений или неравенств;
решение полученного уравнения, неравенства или системы;
интерпретация полученного результата и непосредственно сам ответ на
вопрос задачи.

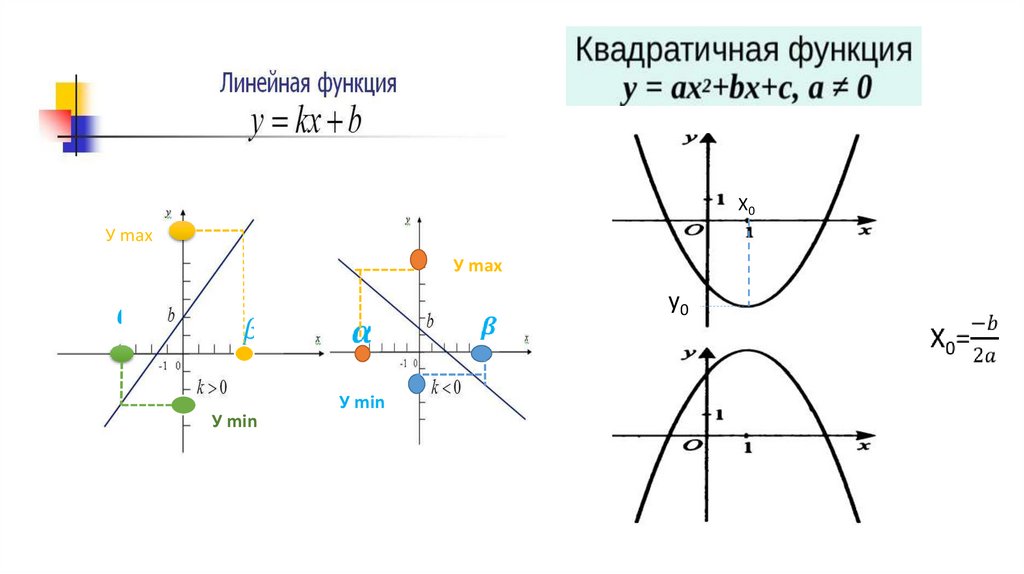
4.

Х0
У max
У max
у0
У min
У min

5.

Задача 1. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый
из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или
3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день.
При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится
сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты
договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее
количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести
завод?
р- производительность труда t – продолжительность рабочего дня m – масса металла, добываемого за день
n – количество рабочих, занятых добычей конкретного металла
Al
n
p
m
Ni
Шахта
Всего рабочих
t
n
p
1
100
5
1
3
2
300
5
3
1
m

6.

Задача 1. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из
которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг
никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При
этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится
сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты
договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее
количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести
завод?
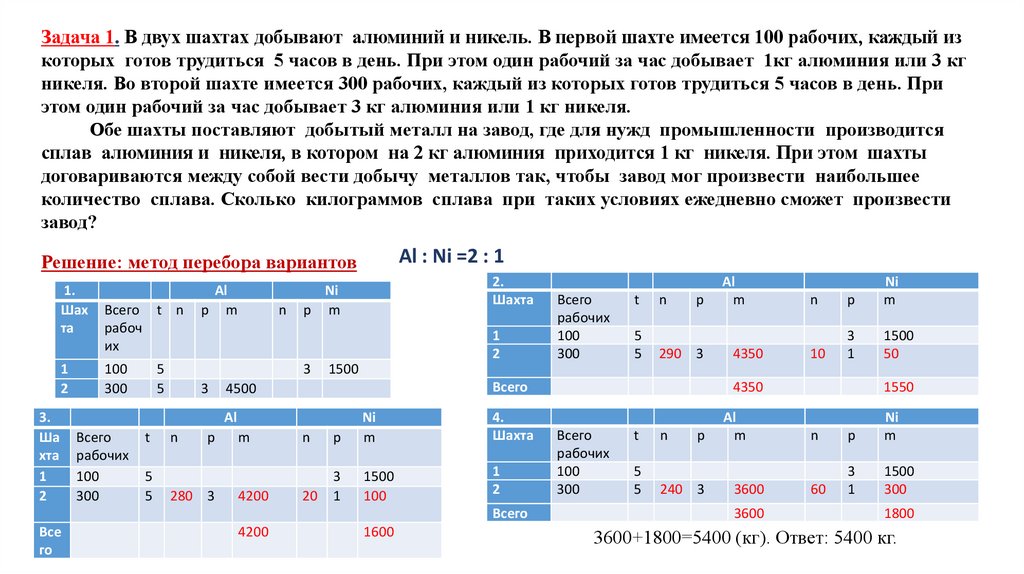
Al : Ni =2 : 1
Решение: метод перебора вариантов
1.
Шах
та
1
2
3.
Ша
хта
1
2
Всего t n
рабоч
их
100
300
5
5
Al
p m
n
1
2
3
3
t
5
5
n
p
280 3
4200
n
p
Ni
m
20
3
1
1500
100
4.
Шахта
1
2
Всего
Все
го
4200
t
5
5
n
p
290 3
Всего
4500
m
Всего
рабочих
100
300
Al
m
4350
n
p
Ni
m
10
3
1
1500
50
1500
Al
Всего
рабочих
100
300
2.
Шахта
Ni
p m
1600
4350
Всего
рабочих
100
300
t
5
5
n
p
240 3
Al
m
3600
3600
1550
n
p
Ni
m
60
3
1
1500
300
1800
3600+1800=5400 (кг). Ответ: 5400 кг.

7.

Задача 1. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из
которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг
никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом
один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав
алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются
между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава.
Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: метод логических рассуждений и сотавления уравнения
1.
Al
Шахта Всего t n
рабо
чих
1
100
5
p
2
3
300
5
m
n
p
3
4500
2.
Шахта
Ni
m
1500
Al : Ni =2 : 1
Al
Всего
рабочих
t
1
100
5
2
300
5
Всего
n
х
p
3
m
5*3*х
n
p
Ni
m
3
1500
300-х 1
5*3*х
5(300-х)
5(300-х)+1500
5*3*х = 2(5(300-х)+1500)
15х = 6000-10х
Х=240
240 рабочих – алюминий, 60 рабочих - никель
5*3*240 =3600(кг) -алюминия
5*60+1500 = 1800 (кг) - никеля
3600+1800 = 5400(кг). Ответ:5400 кг.

8.

Задача 1. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из
которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1кг алюминия или 3 кг
никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При
этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится
сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты
договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее
количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести
завод?
Al : Ni =2 : 1
Решение: метод исследования функции
5х+15у=2(1500-15х+1500-5у)
Al
Шахта
Ni
n
p
m
n
5 х
1
5х
100-х 3
5*3*(100-х)
5х+15у=6000-30х-10у
35х+25у=6000
у=240-1,4х
5 у
3
5*3*у
300-у 1
5*1*(300-у)
М =-10х +10(240-1,4х)+3000
15(100-х)+5(300-у)
М = -24х+5400
t
1
Всего
рабочих
100
2
300
Всего
5х+15у
М = (5х+15у) + 15(100-х)+5(300-у)
p
m
М = 5400
М = 5х+15у+1500-15х+1500-5у
М = -10х+10у+3000
Ответ: 5400 кг
0 х 100
max

9.

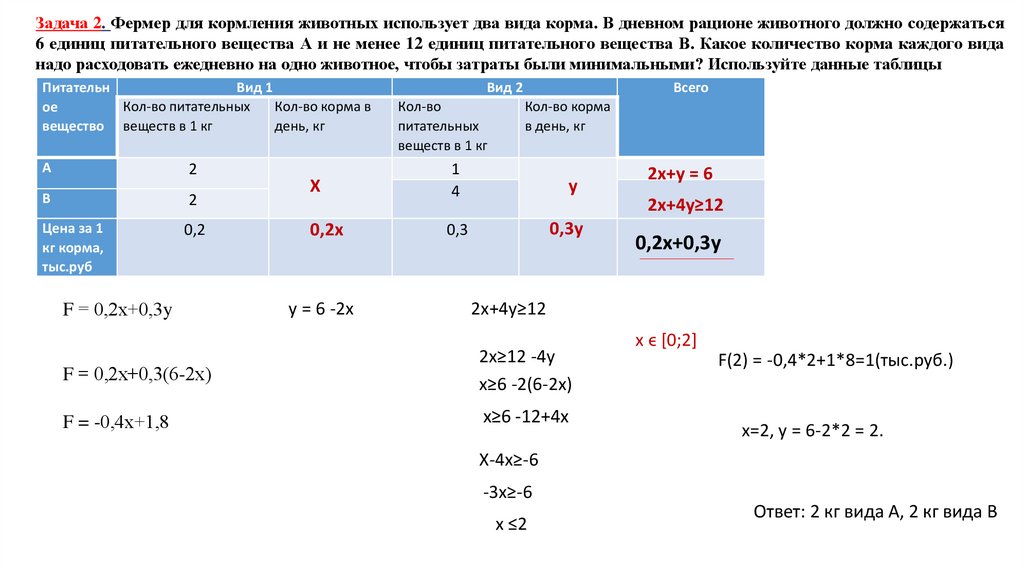
Задача 2. Фермер для кормления животных использует два вида корма. В дневном рационе животного должно содержаться
6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма каждого вида
надо расходовать ежедневно на одно животное, чтобы затраты были минимальными? Используйте данные таблицы
Питательн
Питательное
Количество
Вид 1питательных
Кол-во питательных
корма в
ое вещество
веществ в 1Кол-во
кг корма
кг корма день,
вещество веществ в1 1вид
2 видкгкорма
A
2
1
B
4
А
2 2
Цена 1 кг корма,
Х0,3
0,2
В
2
тыс. руб.
Цена за 1
кг корма,
тыс.руб
0,2
F = 0,2х+0,3y
0,2х
у = 6 -2х
Вид 2
Кол-во
питательных
веществ в 1 кг
Всего
Кол-во корма
в день, кг
1
4
у
0,3у
0,3
2х+у = 6
2х+4у≥12
0,2х+0,3y
2х+4у≥12
F = 0,2х+0,3(6-2х)
2х≥12 -4у
х≥6 -2(6-2х)
F = -0,4х+1,8
х≥6 -12+4х
х ϵ [0;2]
F(2) = -0,4*2+1*8=1(тыс.руб.)
х=2, у = 6-2*2 = 2.
Х-4х≥-6
-3х≥-6
х ≤2
Ответ: 2 кг вида А, 2 кг вида В

10.

Задача 3.Часть денег от капитала 400 млн руб. размещена в банке под 12 % годовых, а другая часть инвестирована в
производство, причем через год эффективность вложения ожидается в размере 250 % (то есть вложенная сумма х руб.
оборачивается в размере 2,5х руб.), затем отчисляются деньги на издержки, которые задаются квадратичной зависимостью
0,0022x2. Прибыль от производства облагается налогом в 20 %. Как распределить капитал между банком и производством,
чтобы через год получить максимальную прибыль от размещения денег в банк и вложения денег в производство? Сколько
рублей составит эта прибыль?
Было
Банк
Стало
Издержки
Налог
400-х 1,12(400-x)
Осталось
1,12(400-x)
Производство
х
2,5х
0,0022x2
20%
0,8(2,5x-0,0022x2 )
F= 1,12(400-x)+ 0,8(2,5x-0,0022x2 )-400
F= 448-1,12x+2x-0,8* 0,0022x-400
F=−0,8⋅0,0022x2​+0,88x+48.
Ответ:158 млн.руб.
F(250)= −0,8⋅0,0022*250​2​+0,88*250+48=-110+220+48=158 (млн.руб).

11.

Задача 4.В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В
первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день
требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется y2 человеко-часов труда. Обе области поставляют добытый
металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля.
При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава.
Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
50
КолВремя
во
рабоч
их
Кол-во
рабочих
Аl
Добывает
один рабочий за
час,кг
0,2
1
50
10
х
2
50
10
у
Ni
Всего
металла за день
2х
Кол-во рабочих
50-х
Добывает
один рабочий за
час,кг
0,1
Всего
1(50-x)
50- У
Всего
500-10у=40у
У=10
10 у = Х2

12.

F ' (20) < 0
+
10 т.max
F '(1)>0
=60 +6 +24=90 (кг)
Ответ: 90 кг

13.

Задача 5. Саша положил некоторую сумму в банк на 4 года под 10% годовых. Одновременно с ним Паша
такую же сумму положил на два года в другой банк под 15% годовых. Через два года Паша решил продлить
срок вклада еще на 2 года. Однако к тому времени процентная ставка по вкладам в этом банке изменилась и
составляла уже p% годовых. В итоге через четыре года на счету у Паши оказалась большая сумма, чем у
Саши, причем эта разность составила менее 10% от суммы, вложенной каждым первоначально. Найдите
наибольшее возможное целое значение процентной ставки.
Сумма,
тыс.руб
Саша х
Паша х
Срок %
4г
2г
Срок
10
15 2г
%
Стало
1,14х
р
<0,1х
р <8,7….
Ответ:8

14.

Задача 6.Баржа грузоподъемностью 134 тонны перевозит контейнеры типов А и В. Количество загруженных на баржу
контейнеров типа В не менее чем на 25% превосходит количество загруженных контейнеров типа А. Вес и стоимость
одного контейнера типа А составляет 2 тонны и 5 млн руб., контейнера типа В – 5 тонн и 7 млн руб. соответственно.
Определите наибольшую возможную суммарную стоимость (в млн руб.) всех контейнеров, перевозимых баржей при
данных условиях.
Кол-во
контей
неров
А Х
В у
Масса
одного
контейнера
Масса всех
контейнеров
Стоимость
контейнера
Стоимость всех
контейнеров
2
5
2х
5у
5
7
5х
7у
S =5х+7у
2х+5у≤134
у≥1,25х
2S-14у+25у≤670
у=20
11у≤670-2S
S≤670-2S
S≤223⅓
Ответ:220 млн.руб.

15.

Задача 7.Иван положил в банк некоторую сумму денег на 4 года. Перед началом каждого года он выбирает одну из двух схем
начисления прибыли в наступающем году:
1) к его счету прибавляется 10% от находящейся на счете суммы;
2) к его счету прибавляется 5% от находящейся на счете суммы и 50 тысяч рублей.
Известно, что по прошествии 4 лет Иван максимально может получить 417967 рублей прибыли, если будет оптимально
выбирать схему начисления прибыли. Сколько рублей положил на счет Иван? Если возможны несколько вариантов ответов,
найдите хотя бы один.
Схе
ма
Сумма,
тыс.руб
%
Сумма с %
через год
А
Х
10
1,1х
В
Х
5
1,05х+50
1,1х-1,05х-50=0,05х-50
1)Х=1000 А-В =0, А=В
2)х<1000, А-В – отриц.число,
В - выгоднее
3)х >1000, А-В – полож.число,
выгоднее схема А
3) x⩾1000 1,14х-х = 1,4641х-х = 0,4641х = 464,1 тыс рублей = 464100 руб
Год
1
2
3
4
Схема
В
ВА или ВВ
ВАА или ВАВ или ВВА или ВВВ
ВААА или ВААВ или ВАВА или ВАВВ или ВВАА или ВВАВ или ВВВА или ВВВВ
ВААА:
(1,05 ∙ х+50) ∙1,13−х=417,967
х≈ 883,957
ВААB:
((1,05∙ х+50) ∙ 1,12) ∙1,05+50−х=417,967
х≈ 911,435
ВАBA:
(((1,05 ∙ х+50)∙1,1)∙ 1,05+50)∙ 1,1−х=417,967
х≈ 896,466
ВАBB:
(((1,05 ∙ х+50)∙1,1)∙ 1,05+50)∙
1,05+50−х=417,967
х≈ 932,118

16.

Задача 6.Иван положил в банк некоторую сумму денег на 4 года. Перед началом каждого года он выбирает одну из двух
схем начисления прибыли в наступающем году:
1) к его счету прибавляется 10% от находящейся на счете суммы;
2) к его счету прибавляется 5% от находящейся на счете суммы и 50 тысяч рублей.
Известно, что по прошествии 4 лет Иван максимально может получить 417967 рублей прибыли, если будет оптимально
выбирать схему начисления прибыли. Сколько рублей положил на счет Иван? Если возможны несколько вариантов
ответов, найдите хотя бы один.
Схе
ма
Сумма,
тыс.руб
Сумма с %
через год
%
А
Х
10
1,1х
В
Х
5
1,05х+50
Год
1
2
3
4
ВBAA:
(( 1,05∙ х+50) ∙ 1,05+50)∙1,12−х=417,967
х=880
ВBАB:
(( 1,05∙ х+50) ∙ 1,05+50)∙1,1 ∙1,05+50−х=417,967
х≈ 912,915
Схема
В
ВА или ВВ
ВАА или ВАВ или ВВА или ВВВ
ВААА или ВААВ или ВАВА или ВАВВ
или ВВАА или ВВАВ или ВВВА или
ВВВВ
ВBBА:
(((1,05 ∙ х+50)∙1,05+50)∙ 1,05+50)∙ 1,1−х=417,967
х≈ 894,626
ВBBB:
(((1,05 ∙ х+50)∙1,05+50)∙ 1,05+50)∙ 1,05+50−х=417,967
х≈ 939,466
Ответ:880000 рублей

17.

Критерии проверки и оценка решений задания 17
Задание №17 – это текстовая задача с экономическим содержанием.
Содержание критерия
Баллы
3
Обоснованно получен верный ответ
Верно построена математическая модель, решение сведено к
исследованию этой модели и получен результат:
2
— неверный ответ из-за вычислительной ошибки;
— верный ответ, но решение недостаточно обосновано
Верно построена математическая модель, решение сведено к
1
исследованию этой модели, при этом решение может быть не
завершено
Решение не соответствует ни одному из критериев,
0
перечисленных выше
Максимальный балл
3