Історичні відомості про прогресії

1. найціннішим є використання набутих знань у життєвих ситуаціях.

2. Історичні відомості про прогресії

3.

► Слово “прогресія” походить від
латинського слова “progressio” і
означає “рух уперед”
(як і слово “прогрес”).
Уперше цей
термін як
математичний
вживається у
працях римського
вченого Боеція
(V - VIст.).

4. Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е.

5. АНГЛІЯ XVIII століття

В XVIII ст. в англійських підручниках
з’явилися позначення
арифметичної і геометричної
прогресії.
Арифметична
Геометрична

6. Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса:

“Нехай тобі сказали:
розділи десять мір
ячменю між 10
чоловіками так, щоб
різниця між кожним
чоловіком і його
сусідом становила 1/8
міри ячменю ”.

7. У папірусі подається не тільки текст задачі, але й пропонується правило для обчислення частки першої з десяти осіб.

8. З досліджень вавилонських клинописних текстів епохи Хаммурані (XVIII cт. до н. е.) бачимо, що і в стародавньому Вавилоні

розв’язування деяких питань господарського
і наукового характеру приводимо до
арифметичної і геометричної прогресії.

9.

У Стародавній Греції
в часи Евкліда і Архімеда (ІІІ ст. до н. е.)
властивості прогресій розглядались у зв’язку
з теоретичними дослідженнями. Так, у книзі
Евкліда “Начала” подається формула суми
трьох членів геометричної прогресії.

10.

У нас задачі на прогресії вперше
зустрічаються в одній з
найдавніших пам’яток руського
права, в “Руській правді”,
складеній при
Ярославі Мудрому
в ХІ столітті.

11.

Там є стаття, присвячена
обчисленню приплоду від
22 овець за 12 років, при
умові, що кожна вівця
щорічно приносить одну
овечку і одного барана.

12.

Значна кількість задач на прогресії
міститься в чудовій пам’ятці
математичної літератури
початку XVIII cт. “Арифметиці”
Л. П. Магніцького.

13.

Зі знаходженням суми членів арифметичної
прогресії пов’язана така цікава історія.
Відомий німецький математик Карл Гаусс
(1777 - 1875) ще у школі виявив блискучі
математичні здібності. Якось учитель
запропонував учням знайти суму перших
ста натуральних чисел. Маленький Гаусс
розв’язав цю задачу за хвилину.
Зміркувавши, що суми 1+100, 2+99 і т. д.
рівні, він помножив 101 на 50, тобто число
таких сум. Інакше кажучи, він помітив
закономірність, яка властива
арифметичній прогресії.

14. Означення і властивості

(аn)-арифм. прогресія
аn+1 = аn + d;
► (аn)-n-й член арифметичної
прогресії є середнім арифметичним двох сусідніх з ним членів.
аn = an 1 an 1
2
Якщо (аn)- скінченна
арифметична прогресія, то
a1 an a2 an 1 a3 an 2 const
Будь-яка арифм. прогресія (аn)
може бути записана формулою
аn = kn+b, де k i b – числа.
► (вn)-геометр.прогресія
вn+1 = вn . q
► (вn)- n-й член
геометричної
прогресії є середнім
геометричним двох
сусідніх з ним членів.
вn = b b
n 1
n 1
► Якщо (вn)- скінченна
геометрична прогресія, то
b1 bn b2 bn 1 b3 bn 2 const

15. Формула n-го члена арифметичної та геометричної прогресії та їх суми

(аn)-арифм. прогресія
аn = а1 + d (n – 1).
(аn)- арифм. прогресія
1)
2)
а1 ап
Sn =
n;
2
2а1 d n 1
n
Sn =
2
(вn) - геометр.прогресія
bn = b1 . qn-1;
(вn) - геометр.прогресія
1)
2)
3)
b1 bn q
Sn
, (q 1)
1 q
n
b1 ( q 1)
Sn
, ( q 1)
q 1
b1
S
, (q 1)
1 q

16. Усні вправи

1. Відгадати число:
55
59
63
?

17. Чи будуть всі написані послідовності арифметичними прогресіями?

Усні вправи
Чи будуть всі написані
послідовності арифметичними
прогресіями?
► 5, 7, 9, 11, …
► 20, 10, 0 , -10, …
► 2, 4, 6, 8, …
► 1, 2, 6, 8, …
► 15, 3, -9, …
Вказати номер послідовності, яка не є
арифметичною прогресією.

18. Чи будуть всі написані послідовності геометричними прогресіями?

Усні вправи
Чи будуть всі написані
послідовності геометричними
прогресіями?
► 2, 4, 8, 16, …
► 200, 20, 2, …
► 3, -6, 12, …
► 1, 4, 16, 64, …
► 8, 4, 0, -4, …
Вказати номер послідовності, яка не є
геометричною прогресією.

19. Знайти невідомі елементи в даній прогресії:

(аn) - арифметична прогресія,
а1 = 3, а2 = 10.
1) d - ?; 2) a4 - ?
(аn) - арифметична прогресія,
а1 = 3, d = 2.
3) а7 - ?, 4) а9 -?, 5) а12 - ?.
(вn) - геометрична прогресія,
1
в1 = 40, q = .
2
6) в2 -?,
7) в3 - ?,
8) в4 -?.

20.

Sn =
a1 a n
n
2

21. Задача 2 . (Забавна арифметика, 1910 р.)

Одного разу розумний бідняк попросив у скупого
багатія притулку на 2 тижні на таких умовах: «За
це я тобі першого дня заплачу 1 крб., другого – 2
крб., третього 3 крб., збільшуючи щоденну плату
на 1 крб. Ти ж будеш давати мені милостиню:
Першого дня – 1 коп., другого дня – 2 коп.,
третього – 4 коп., і т.д. збільшуючи щодня
милостиню вдвічі». Багатій з радістю погодився,
вважаючи, що умови вигідні для нього. Скільки
грошей отримав багатій?

22. Розв'язання:

Сума, яку має сплатити бідняк за 14 днів, складає
арифметичну прогресію, в якій а1 = 1 і d =1, S14=
105, тобто 105 крб., а багатій сплачує суму, яка
складає суму геометричної прогресії, в якій а1 =
1, q = 2. Тому S14 =214-1= 16383 коп. або 163
крб.83 коп.
Отже, багатій, отримавши від бідняка 105 крб.,
заплатив йому 163 крб.83 коп., тобто, за те, що
бідняк у нього проживав 2 неділі, багатій
заплатив йому 58 крб.83 коп. (вернувши при цьому
і ті гроші, які одержав від бідняка).

23.

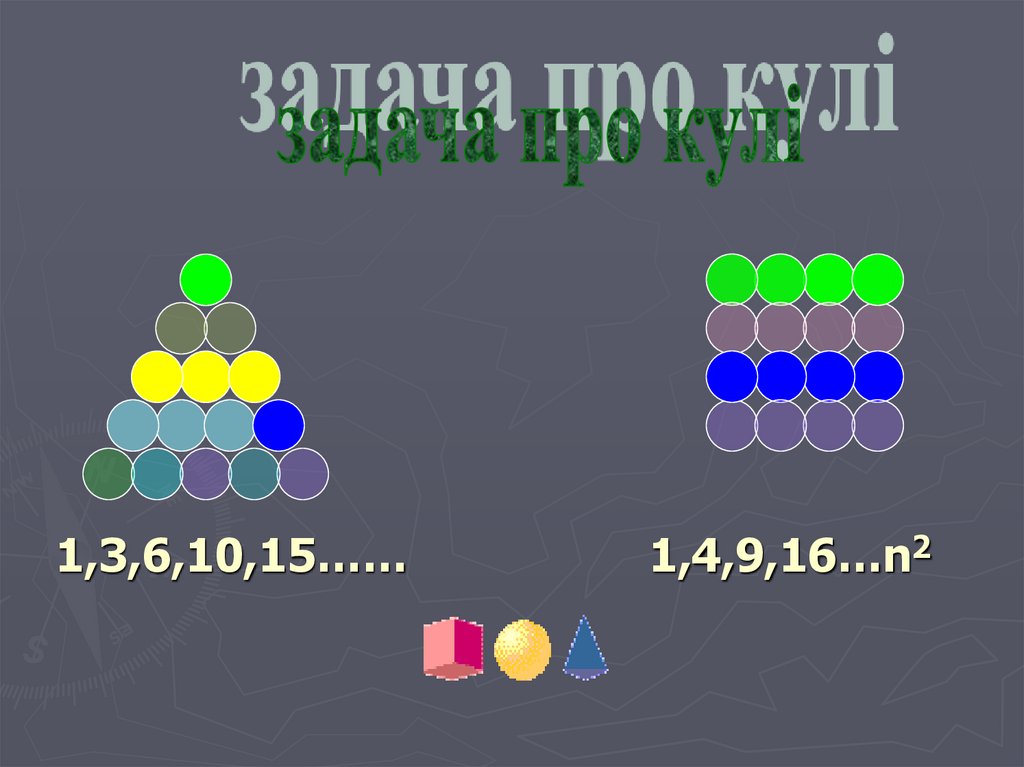
1,3,6,10,15……
1,4,9,16…n2

24.

► Задача 4. Кулі розміщено у формі трикутника
так, що в першому ряду –1 куля, у другому - 2
кулі, у третьому – 3 кулі і т.д.
У скільки рядів розміщено кулі, якщо всього їх
120?
► Розв’язання.
Маємо арифметичну прогресію, в якій а1 =1,
а2= 2, а3= 3, d = 1, Sn = 120, n - ?
Sn =
2 1 (п 1) 1
п
2
n(n+1) = 2 .120, n2 + n - 240 = 0, n1 = 15,
n2=-16 – не задовольняє умови задачі. Тому 120 куль
можна розмістити в 15 рядах.

25. Задача 4. Поливання грядок

Поливання
грядок
Задача 4.
► У городі 30 грядок, кожна довжиною 16м і
шириною 2,5м. Поливаючи грядки,
городник приносить відра з водою з
колодязя, розташованого в 14м від краю
городу, і обходить грядки вздовж межі,
причому води, принесеної за один раз,
вистачає для поливання лише однієї
грядки. Якої довжини шлях проходить
городник, поливаючи весь город? (Шлях
починається і закінчується біля колодязя.)

26. Розв'язання:

Для поливання першої грядки городник проходить
шлях
14 + 2,5 + 16 + 2,5 + 16 + 14 = 65 (м).
Для поливання другої грядки він проходить шлях
14 + 2,5 + 16 + 2,5 + 16 + 2,5 + 2,5 + 14 = 70 (м).
Для кожної наступної грядки потрібно пройти шлях, на
5м довший за попередній.
Маємо2арифметичну
прогресію: 65, 70, 75, …
65 29 5
2
S30 =
30 = 4125 (м).
Відповідь: Городник, поливаючи город, проходить шлях
4,125 км.

27. Трохи гумору

Один з учнів, викликаний до дошки, має
йти від свого місця до дошки по прямій.
Перший крок він робить довжиною 1 м,
другий ½ м, третій 1/4 м і и т. д. так, що
довжина наступного кроку в два рази
менша довжини попереднього. Чи дійде
учень до дошки, якщо відстань місця учня
до дошки по прямій 3 м?

28. Розв’язок

Запишемо послідовність чисел
1 1
1
1; ; ; n 1 ;
2 4
2
b1q b1
Sn
q 1
n
За формулою
Sn 3
n
1
1
Маємо S 2
;
1
1
2
Звідки
Висновок: не дійде!
1
S
2

29. Архітектура

Амфітеатр складається з 10 рядів, в кожному наступному
ряду на 20 місць більше, ніж у попередньому, а в
останньому ряду 280 місць. Скільки людей вміщує
амфітеатр?

30. Розв`язування задачі

Отже,перед нами арифметична прогресія.
Нехай х місць в першому ряду, (х+20) місць в другому ряду,
(х+20+20), тобто. (х+40) місць у третьому ряду і т. д.
a1 x a2 x 20
аn а1 d (n 1)
a10 a1 9d
d 20
a10 280
280 x 9 20
x 100
Отже, 100 місць у першому ряду .
Sn
а1 аn
n
2
S10
а1 а10
10
2
S10
100 280
10
2
Відповідь:1900
S10 1900

31. Розв'язування задач

І рівень
(вn ) - геометрична прогресія,
в1 = 3,
q = 2. в5 - ?
ІІ рівень
(вn ) - геометрична прогресія,
в2 = 6, в4 = 24, в6 - ?
ІІІ рівень
Знайти суму 20 перших членів
арифметичної прогресії (аn), якщо
а7=18,5, а17 = -26,5.

32. Перевірка результатів

І рівень. b5= b1. q4, b5= 3 . 24 = 48, b5= 48.
ІІ рівень. b4= b2. q2, q = 2 . b6= b4 . q2, b6= 96
III рівень.
а а7
а17=а7+10d; d= 17
10
; d=-4,5.
a7= a1+6d, a1= a7 - 6d, a1= 45,5.
2 45,5 4,5 19
10
S20=
2
= 55, S20=55.

33.

Дякую за співпрацю і
до зустрічі !
Домашнє завдання
Опрацювати §19 стор.185
Виконати №19.6, 19.8, 19.13