Механические колебания. Свободные колебания (9 класс)

1.

Механические колебания

2.

Колебания - это движения, которые точно или
приблизительно повторяются через определенный
интервал времени.
Колебания – один
из самых
распространенных
процессов в
природе и технике.

3. Примеры колебаний

•распространение звука
•распространение света
• движение качелей
•движение маятника
часов
•движение поршня ДВС
•землетрясения
•приливы и отливы
• биение пульса
•движение иглы
швейной машины

4.

Механические колебания
Свободные –
колебания в системе
под действием
внутренних сил,
после того как
система выведена из
положения
равновесия.
Вынужденные –
колебания тел под
действием внешних
периодически
изменяющихся сил.

5.

Свободные колебания – это колебания, происходящие
только благодаря начальному запасу энергии
Условия существования свободных
колебаний
•наличие положения устойчивого равновесия
(ПУР);
•равнодействующая сил, действующих на
тело, всегда направлена к ПУР;
•ПУР тело проходит по инерции;
•Сила трения (сопротивления) стремиться к
нулю.

6.

Колебательные системы – это системы,
способные совершать свободные колебания
Колебательные системы Системы не являющиеся
качели;
колебательными
тело на нити;
игла швейной машины;
тело на пружине;
поршень ДВС
струна гитары

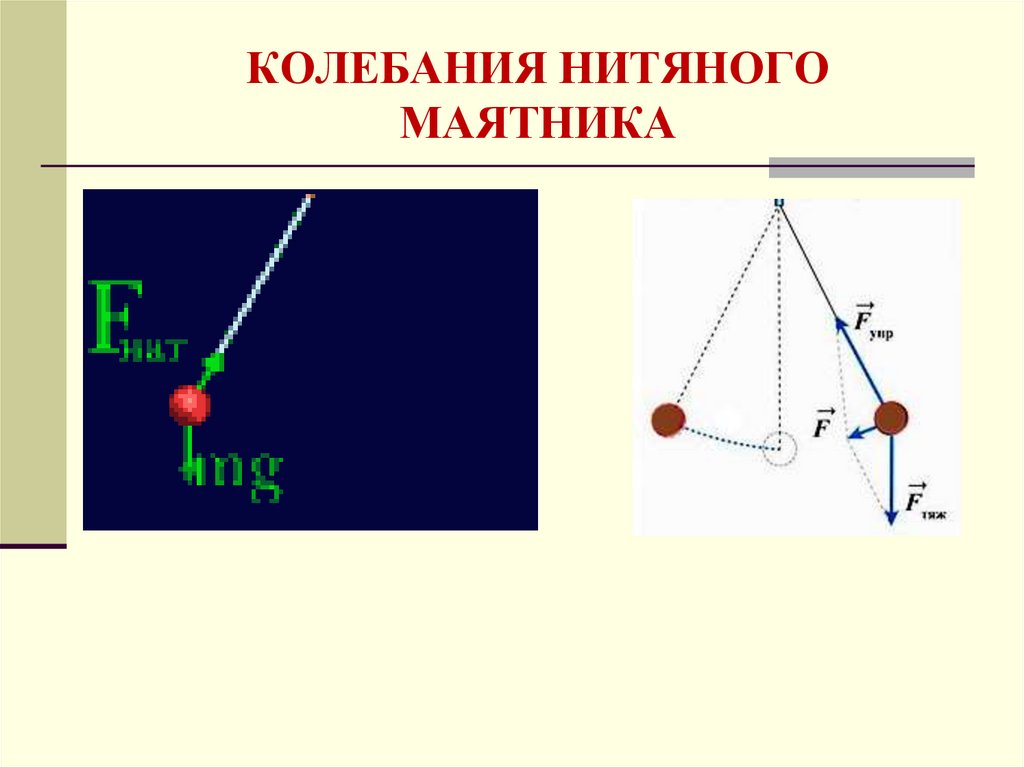
7. КОЛЕБАНИЯ НИТЯНОГО МАЯТНИКА

8. Величины, характеризующие колебательное движение

T – период колебаний – время одного полного
колебания (с)
А - амплитуда колебаний –модуль максимального
отклонения точки от положения равновесия (м)
٧ - частота колебаний - число полных колебаний за
единицу времени (Гц)
1 Гц – это одно колебание в секунду.
Примерно с такой частотой бьется человеческое сердце.

9.

Основные формулы
Период и частота
через число
колебаний и время
Связь частоты и периода колебаний

10.

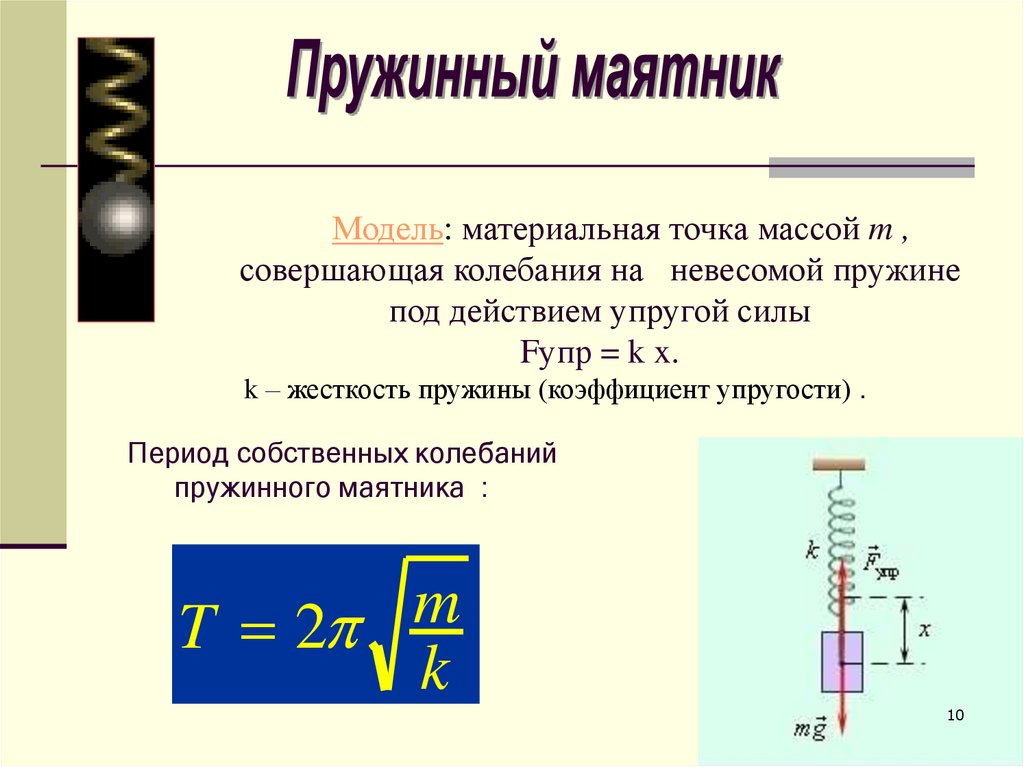
Модель: материальная точка массой m ,
совершающая колебания на невесомой пружине
под действием упругой силы
Fупр = k x.
k – жесткость пружины (коэффициент упругости) .
Период собственных колебаний
пружинного маятника :
m
T 2
k
10

11.

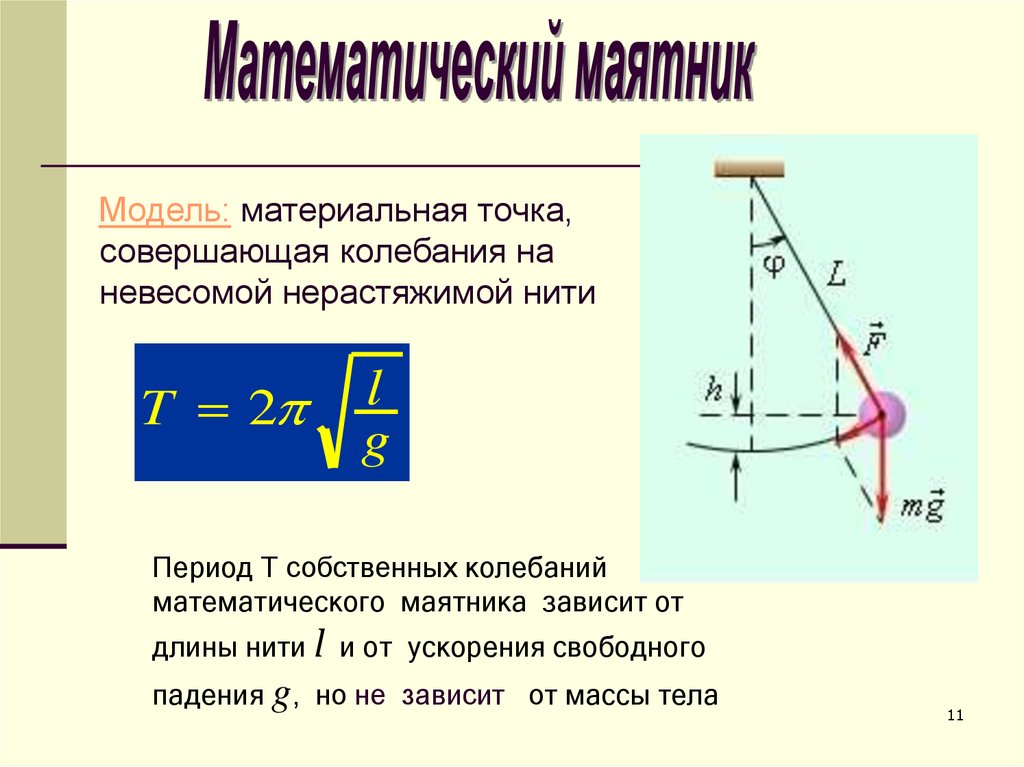
Модель: материальная точка,
совершающая колебания на
невесомой нерастяжимой нити
T 2
l
g
Период Т собственных колебаний
математического маятника зависит от
длины нити l и от ускорения свободного
падения g, но не зависит от массы тела
11

12. Основные формулы

Период колебаний
математического
маятника
Период колебаний
пружинного
маятника
Зависит от:
1.Длины маятника
2.Ускорения
свободного
падения в данном
месте.
НЕ ЗАВИСИТ ОТ
МАССЫ
Зависит от:
1. Массы груза
2. Жёсткости
пружины

13. Развернём колебания по времени

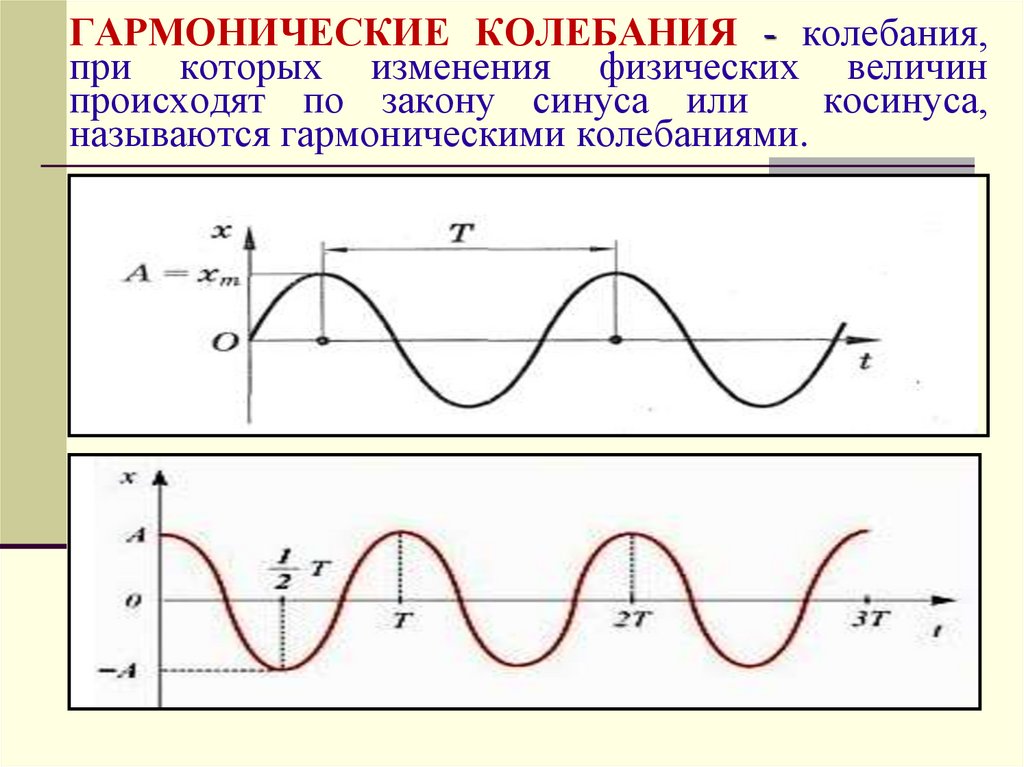
14. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ - колебания, при которых изменения физических величин происходят по закону синуса или косинуса,

называются гармоническими колебаниями.

15.

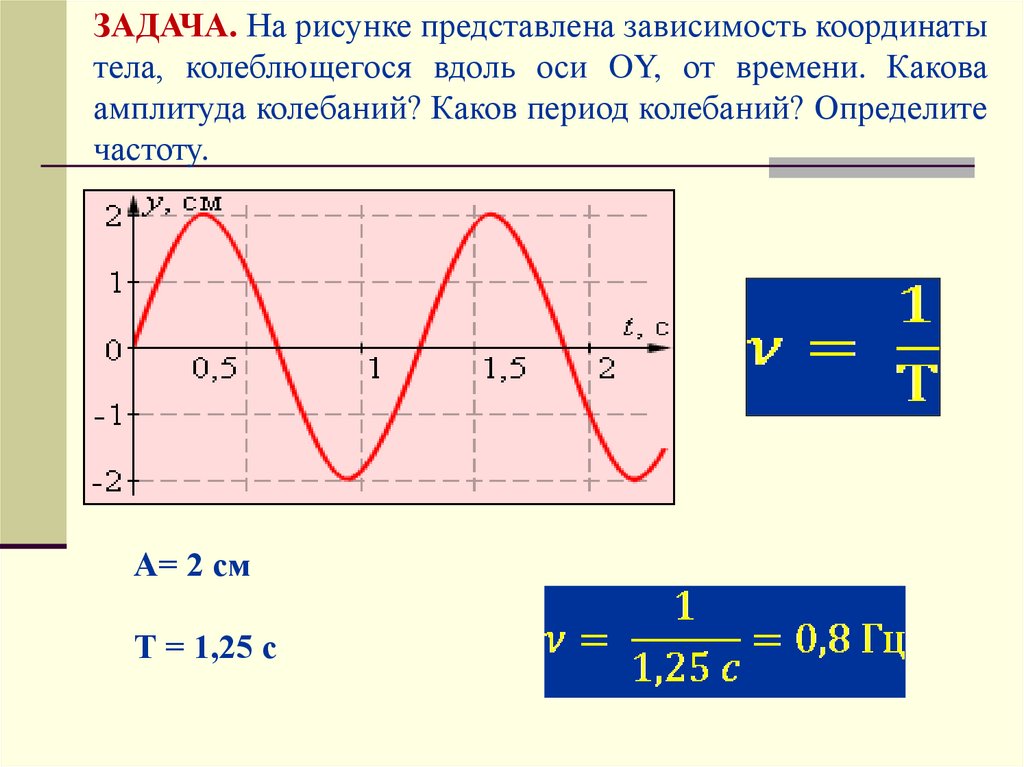
ЗАДАЧА. На рисунке представлена зависимость координаты
тела, колеблющегося вдоль оси OY, от времени. Какова
амплитуда колебаний? Каков период колебаний? Определите
частоту.
А= 2 см
Т = 1,25 с

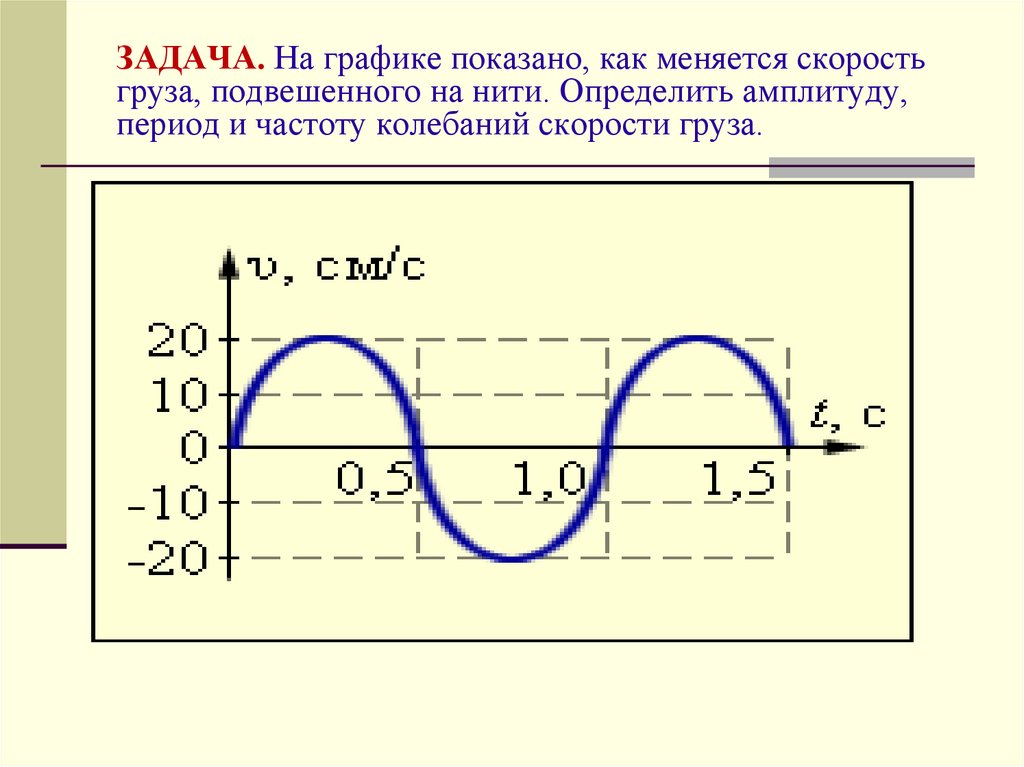
16. ЗАДАЧА. На графике показано, как меняется скорость груза, подвешенного на нити. Определить амплитуду, период и частоту

колебаний скорости груза.

17.

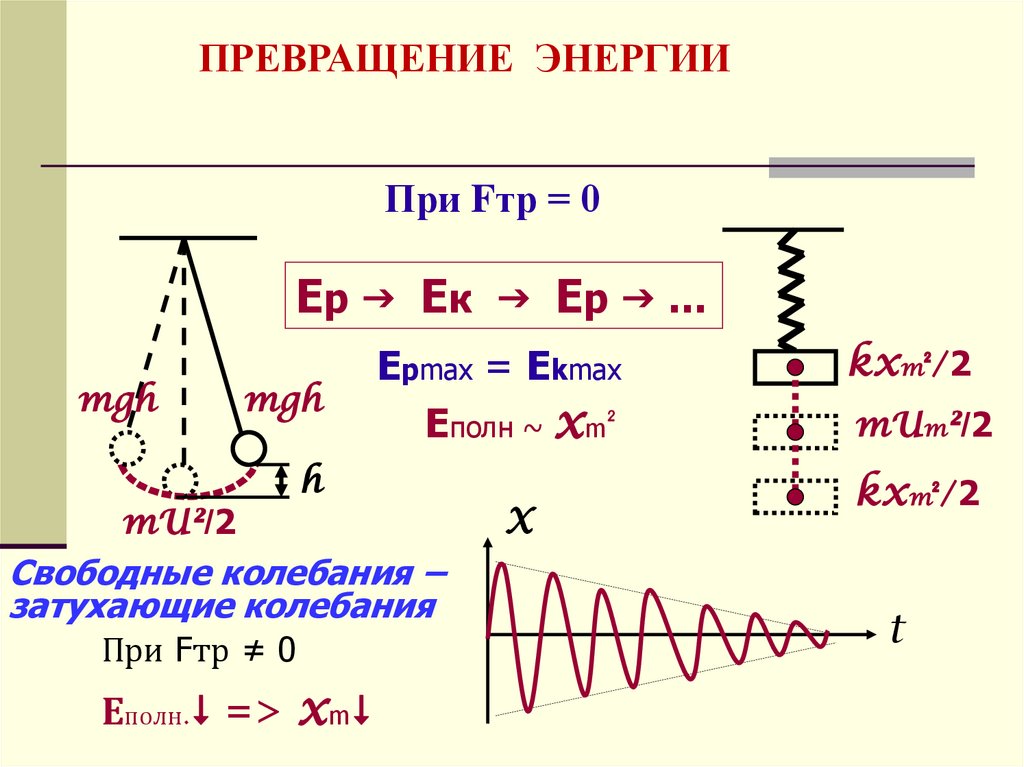
ПРЕВРАЩЕНИЕ ЭНЕРГИИ
При Fтр = 0
Ер Ек Ер …
mgh
mgh
mU²/2
Epmax = Ekmax
Eполн ~ xm²
h
Свободные колебания –
затухающие колебания
При Fтр ≠ 0
Еполн. => xm
X
kxm²/2
mUm²/2
kxm²/2
t

18. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, возникающие под действием внешних, периодически изменяющихся сил (при периодическом

поступлении
энергии извне к КС)
Свободные колебания - колебания строго одной
частоты (собственной частоты КС).
В вынужденных колебаниях частота колебаний
любая, которая определяется вынуждающей силой
Fвын.
Если Fвын. изменяется по закону синуса или
косинуса, то вынужденные колебания будут
гармоническими.
Частота вынужденных колебаний равна частоте
изменения внешней силы

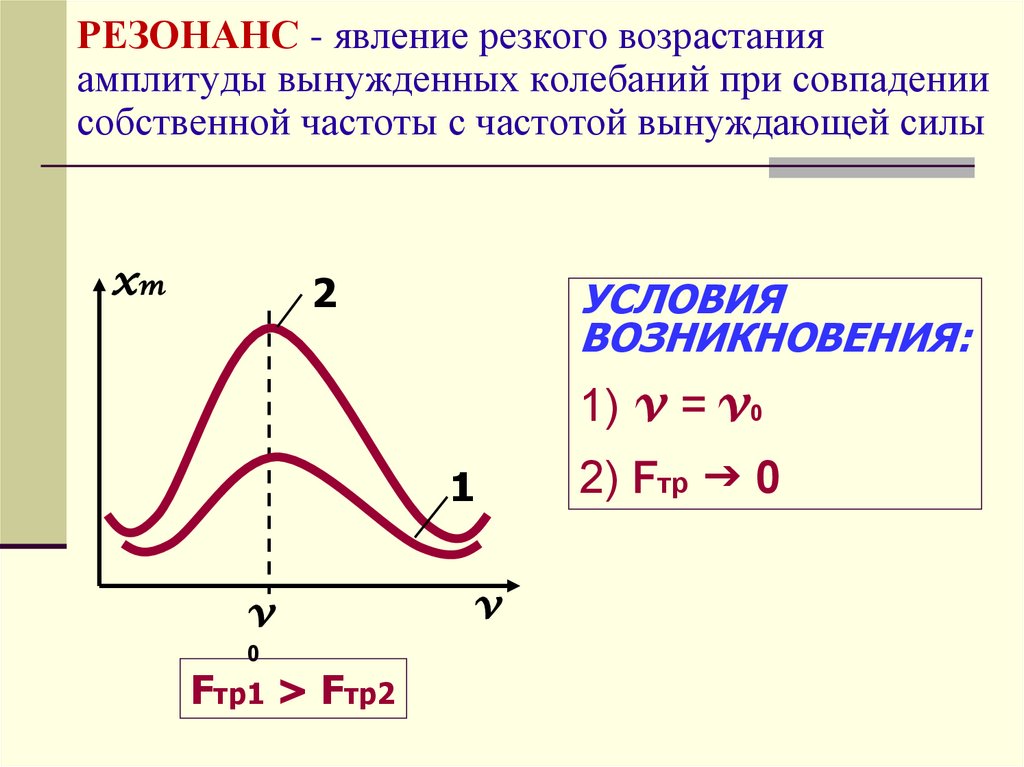
19. РЕЗОНАНС - явление резкого возрастания амплитуды вынужденных колебаний при совпадении собственной частоты с частотой

вынуждающей силы
xm
2
УСЛОВИЯ
ВОЗНИКНОВЕНИЯ:
1) v = v0
1
v
0
Fтр1 > Fтр2
v
2) Fтр 0