Линза. Выпуклые линзы

1.

Линзой называют прозрачное тело, ограниченное с двух сторон
сферическими поверхностями, либо одной сферической и одной
плоской поверхностями.
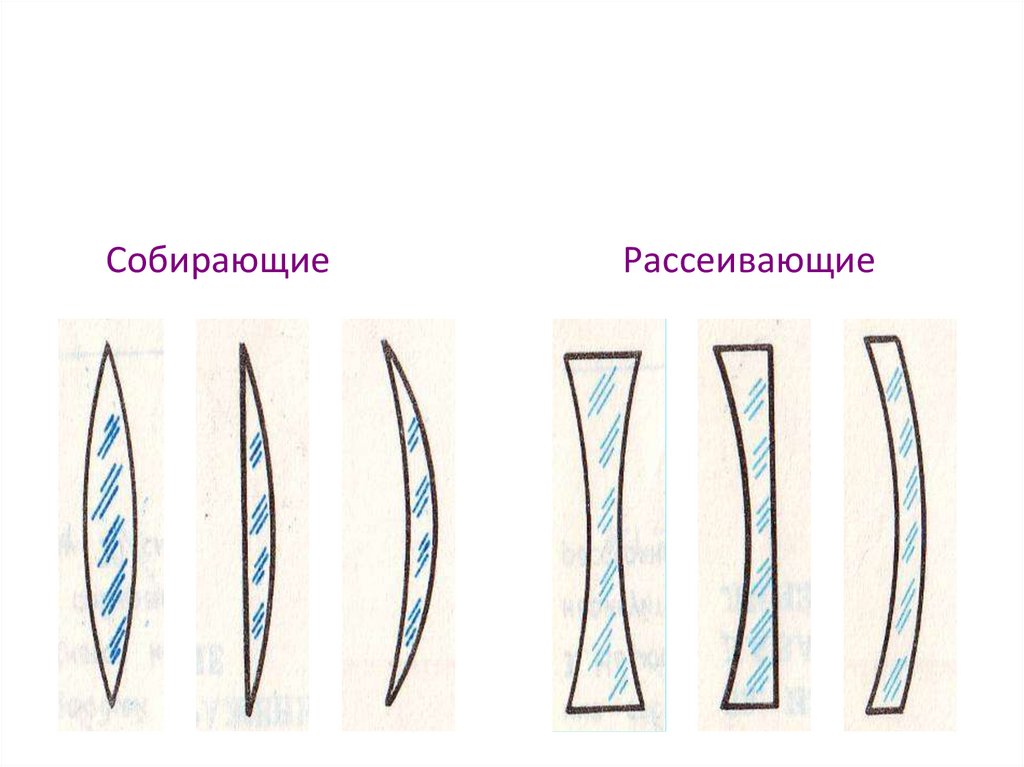
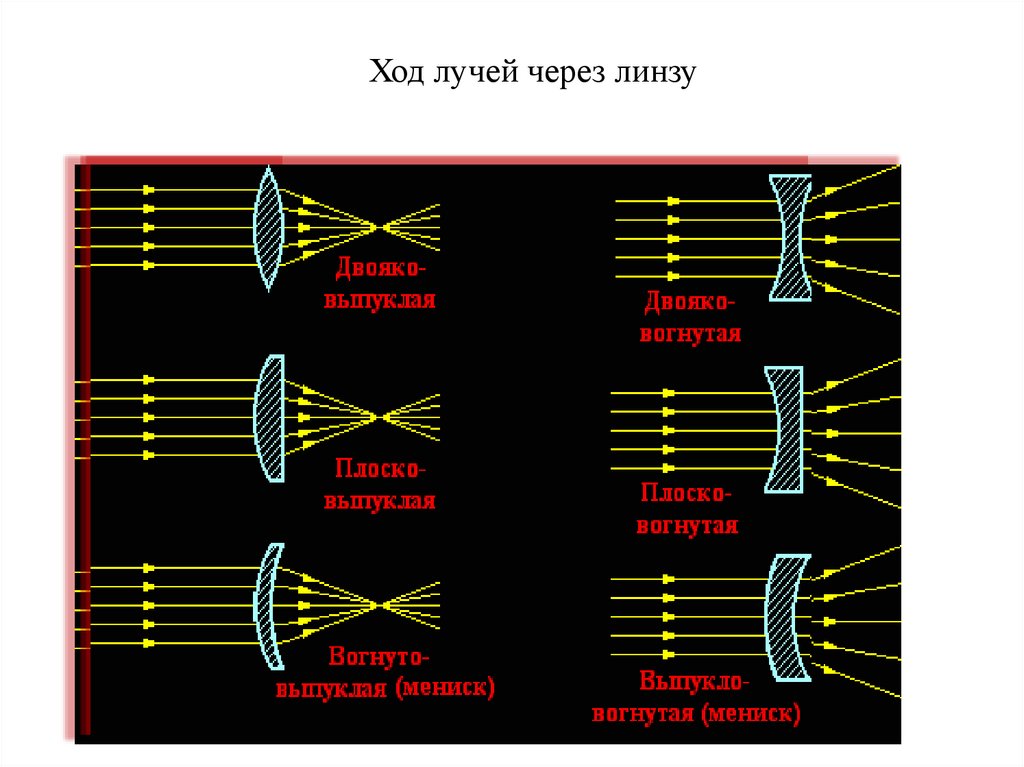
Выпуклые – линзы, у которых края намного тоньше, чем середина.
Вогнутые – линзы, у которых края толще, чем середина

2.

Собирающие
Рассеивающие

3.

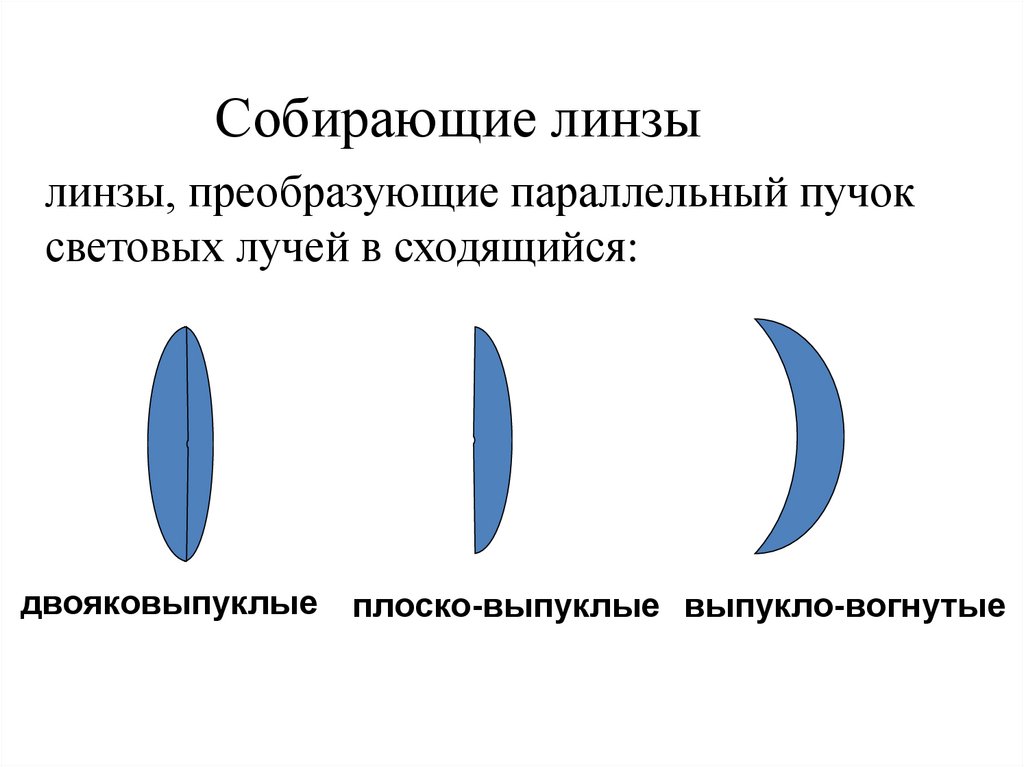
Собирающие линзы
линзы, преобразующие параллельный пучок
световых лучей в сходящийся:
двояковыпуклые
плоско-выпуклые выпукло-вогнутые

4.

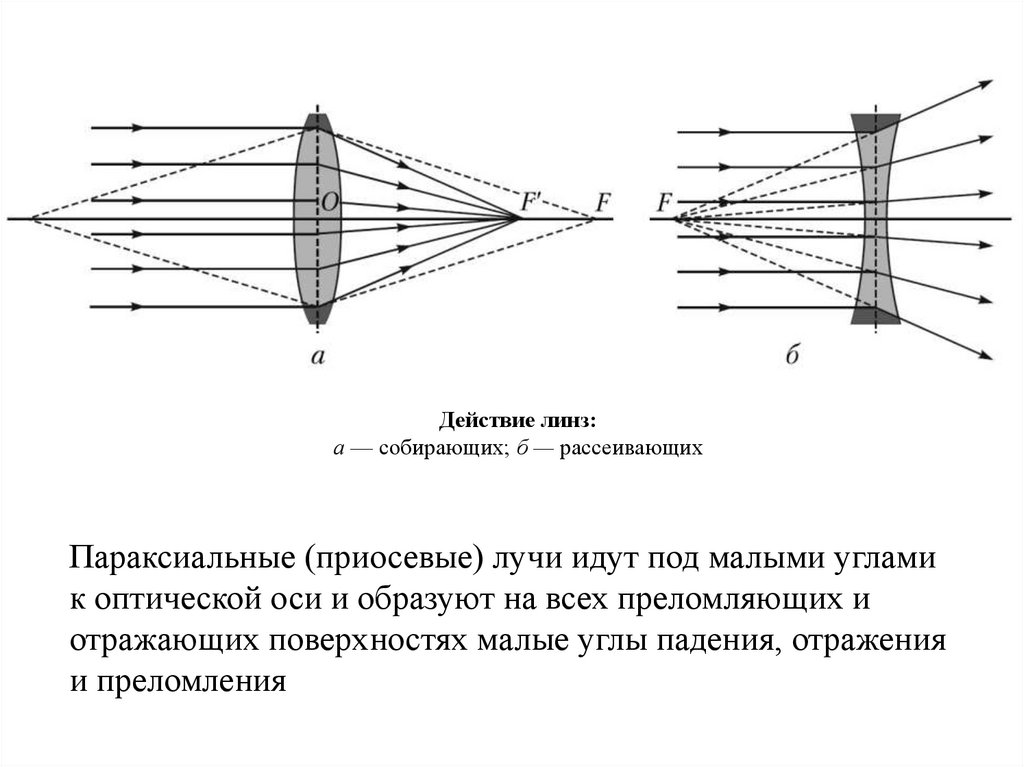
Действие линз:
а — собирающих; б — рассеивающих
Параксиальные (приосевые) лучи идут под малыми углами
к оптической оси и образуют на всех преломляющих и
отражающих поверхностях малые углы падения, отражения
и преломления

5. Основные элементы линзы

О
ГЛАВНАЯ ОПТИЧЕСКАЯ ОСЬ – прямая, проходящая через
центры сферических поверхностей, ограничивающих линзу.
ОПТИЧЕСКИЙ ЦЕНТР – пересечение главной оптической оси с
линзой, обозначается точкой О.
Побочная оптическая ось – любая прямая, проходящая через
оптический центр.

6.

Фокус линзы
Если на собирающую линзу падает пучок лучей,
параллельных главной оптической оси, то после
преломления в линзе они собираются в одной точке F,
которая называется главным фокусом линзы.

7.

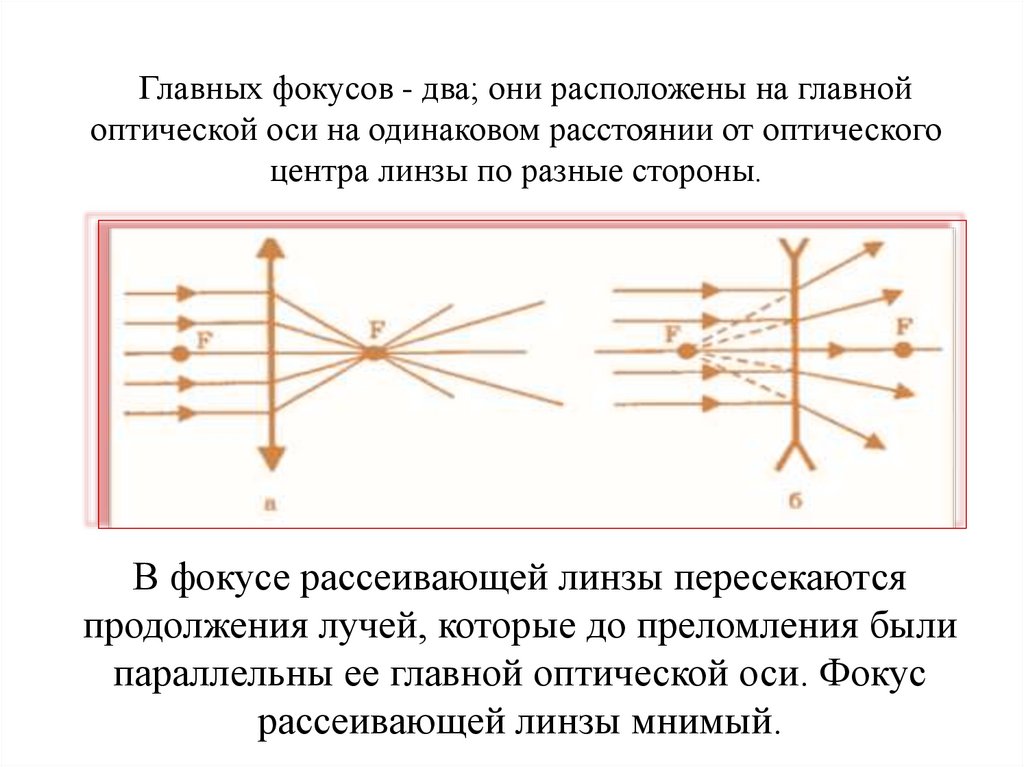
Главных фокусов - два; они расположены на главной
оптической оси на одинаковом расстоянии от оптического
центра линзы по разные стороны.
В фокусе рассеивающей линзы пересекаются
продолжения лучей, которые до преломления были
параллельны ее главной оптической оси. Фокус
рассеивающей линзы мнимый.

8.

Ход лучей через линзу

9.

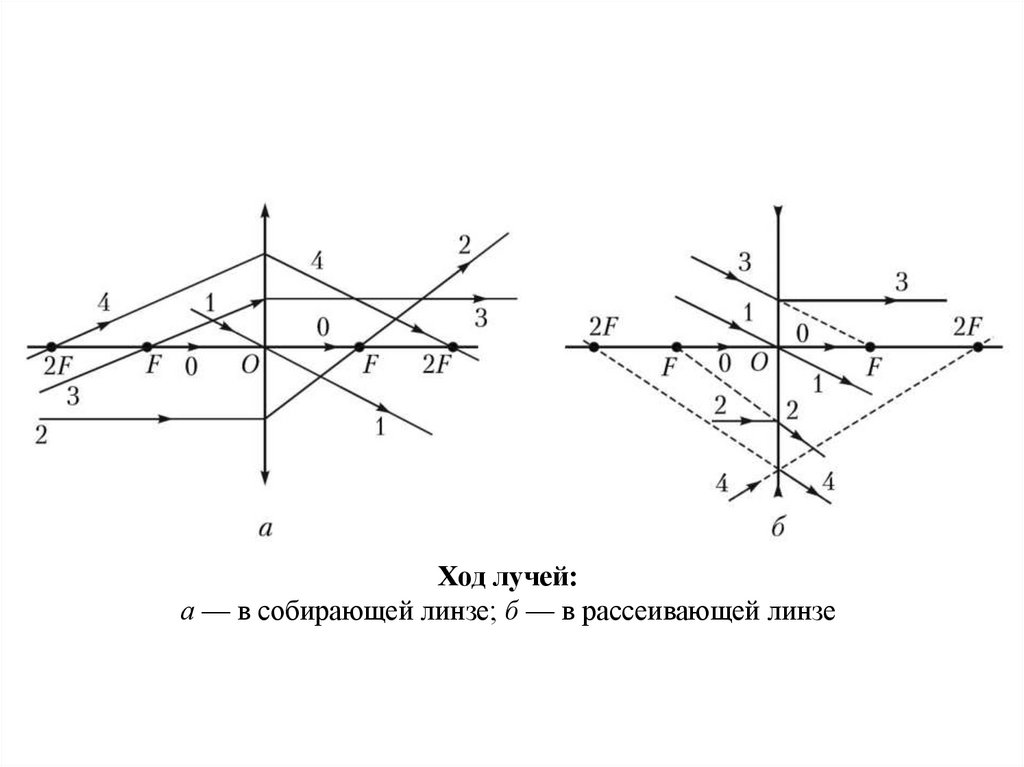
Ход лучей:
а — в собирающей линзе; б — в рассеивающей линзе

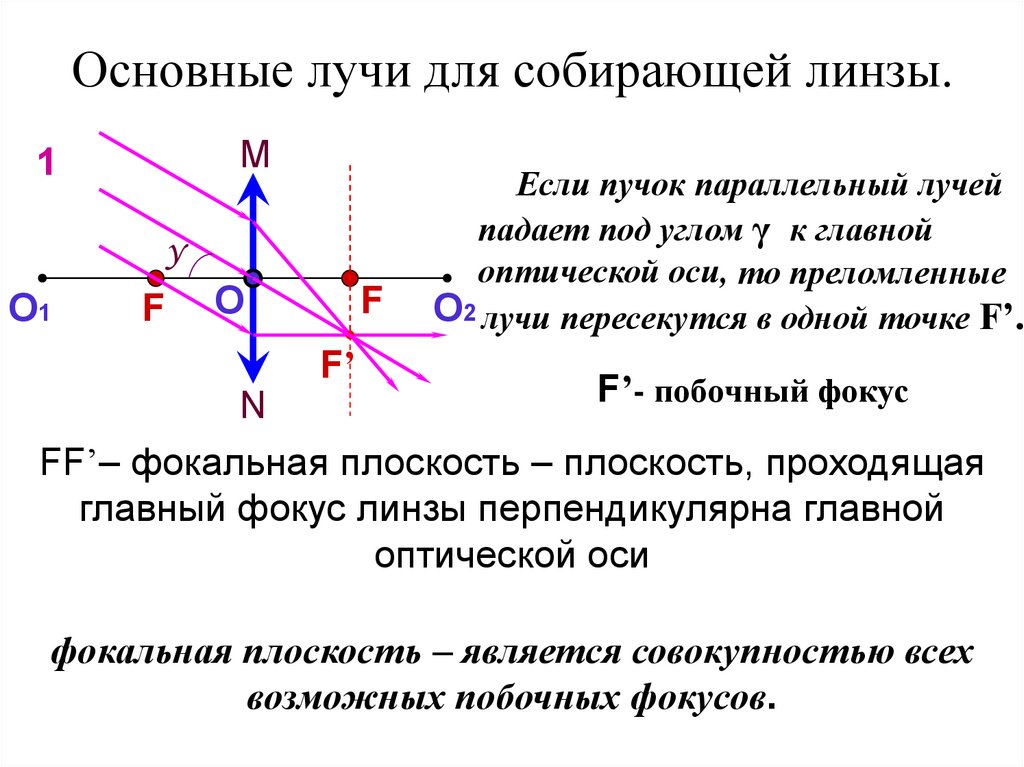
10. Основные лучи для собирающей линзы.

M
1
γ
О1
F
О
F
Если пучок параллельный лучей
падает под углом γ к главной
оптической оси, то преломленные
О2 лучи пересекутся в одной точке F’.
F’
F’- побочный фокус
N
FF’– фокальная плоскость – плоскость, проходящая
главный фокус линзы перпендикулярна главной
оптической оси
фокальная плоскость – является совокупностью всех
возможных побочных фокусов.

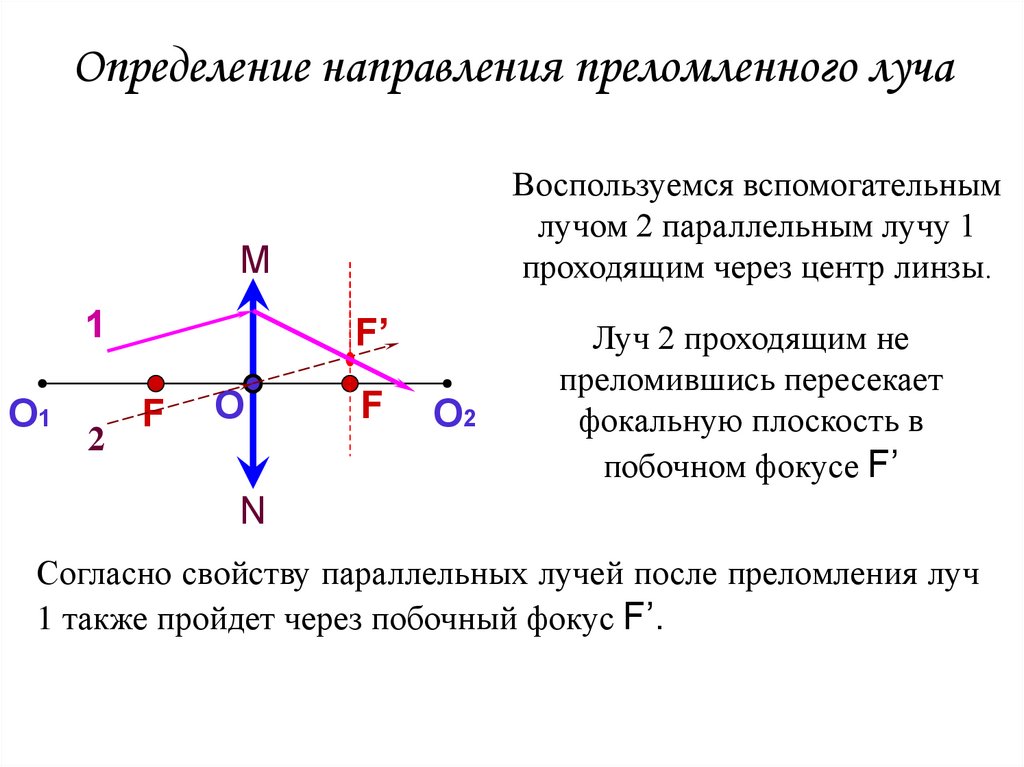
11. Определение направления преломленного луча

Воспользуемся вспомогательным
лучом 2 параллельным лучу 1
проходящим через центр линзы.
M
1
О1
2
F’
F
О
F
О2
Луч 2 проходящим не
преломившись пересекает
фокальную плоскость в
побочном фокусе F’
N
Согласно свойству параллельных лучей после преломления луч
1 также пройдет через побочный фокус F’.

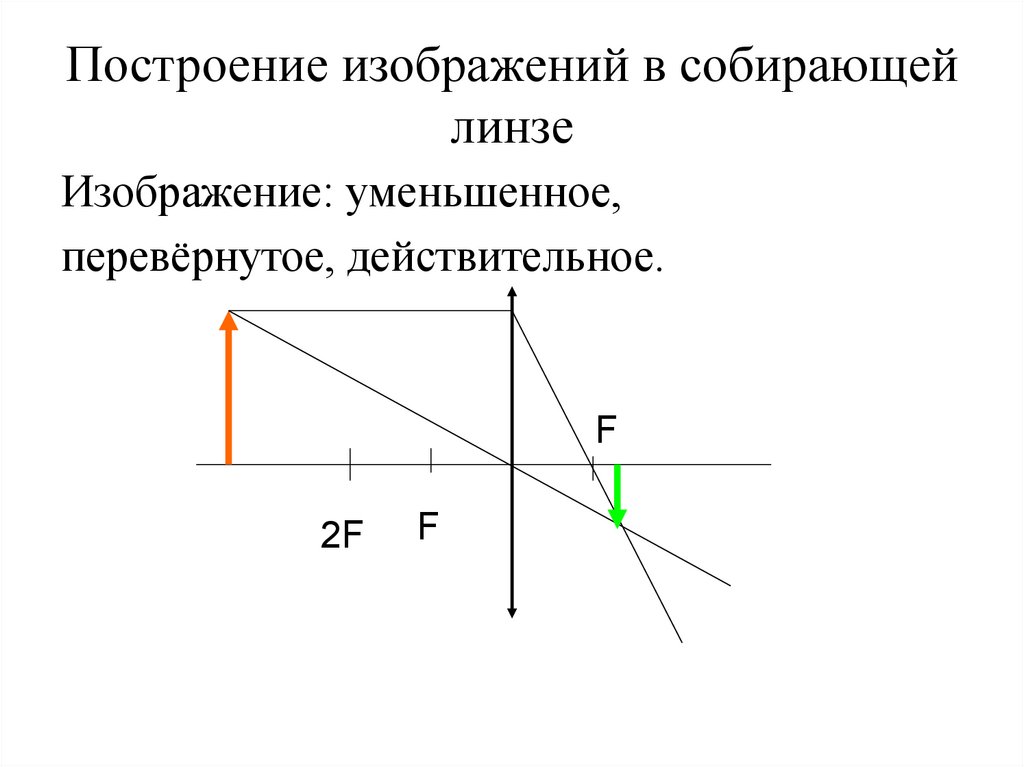
12. Построение изображений в собирающей линзе

Изображение: уменьшенное,
перевёрнутое, действительное.
F
2F
F

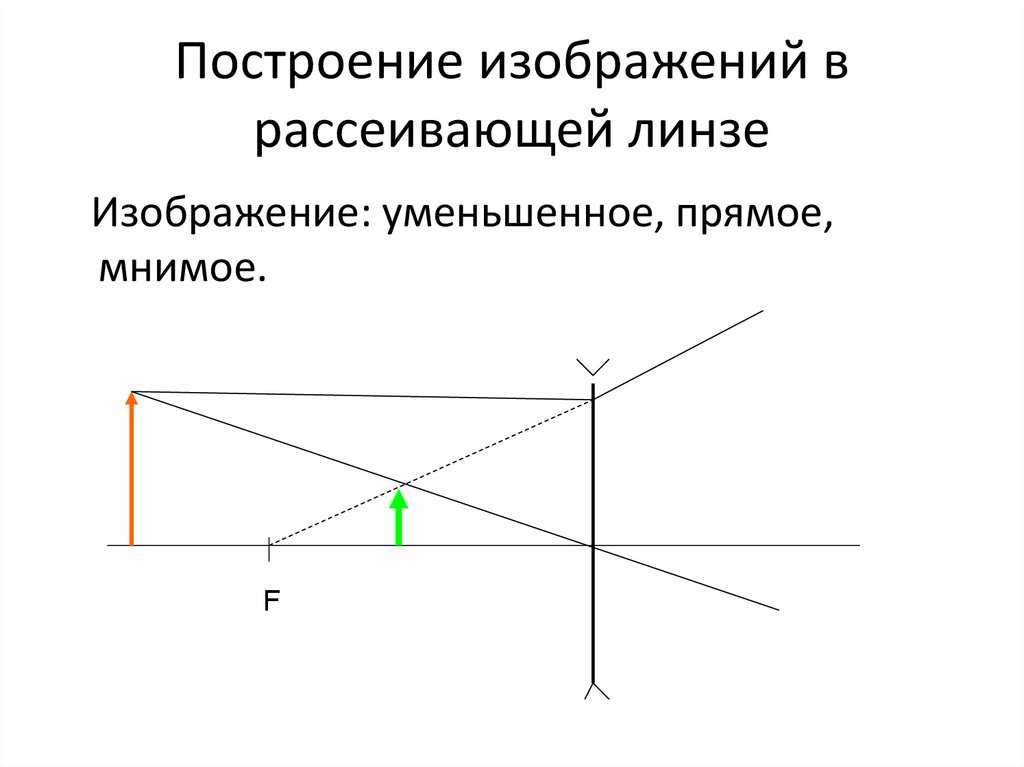
13. Построение изображений в рассеивающей линзе

Изображение: уменьшенное, прямое,
мнимое.
F

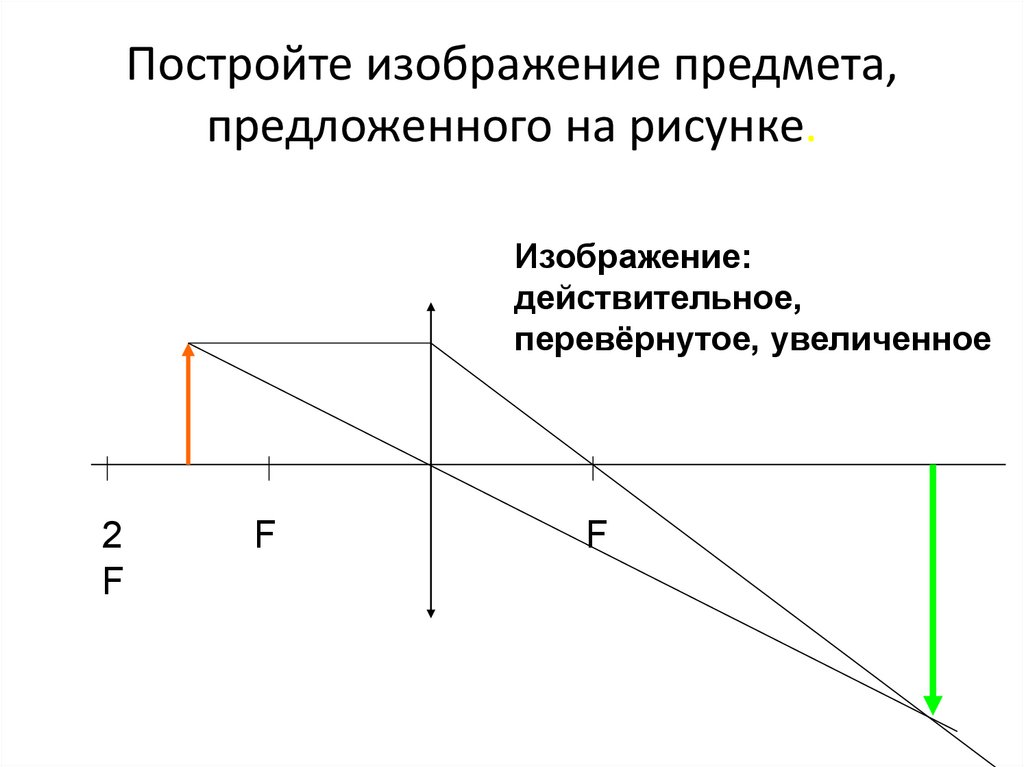
14. Постройте изображение предмета, предложенного на рисунке.

Изображение:
действительное,
перевёрнутое, увеличенное
2
F
F
F

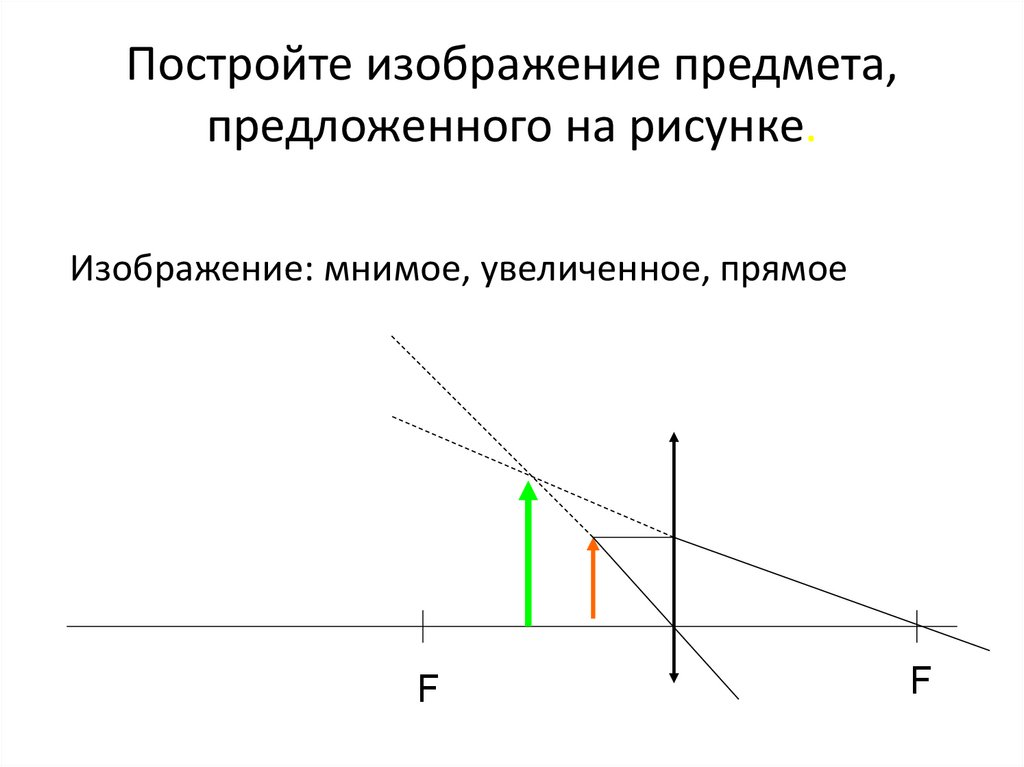
15. Постройте изображение предмета, предложенного на рисунке.

Изображение: мнимое, увеличенное, прямое
F
F

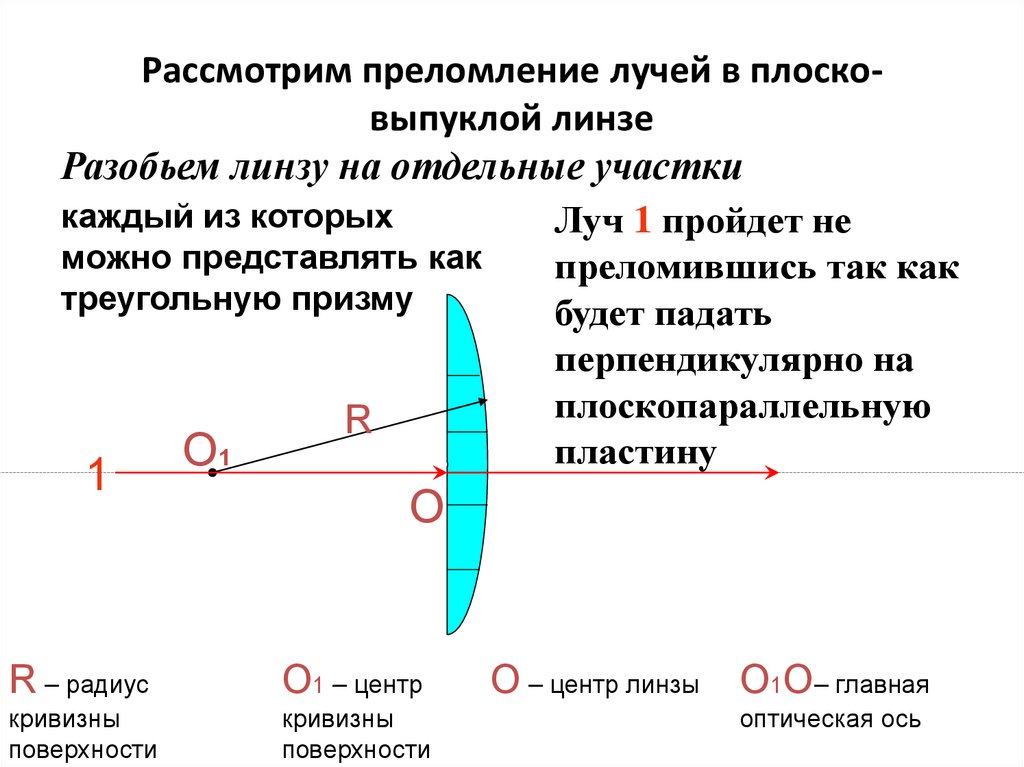
16. Рассмотрим преломление лучей в плоско-выпуклой линзе

Рассмотрим преломление лучей в плосковыпуклой линзе
Разобьем линзу на отдельные участки
каждый из которых
Луч 1 пройдет не
можно представлять как
преломившись так как
треугольную призму
будет падать
перпендикулярно на
плоскопараллельную
R
пластину
О1
1
О
R – радиус
О1 – центр
О – центр линзы О1О– главная
кривизны
поверхности
кривизны
поверхности
оптическая ось

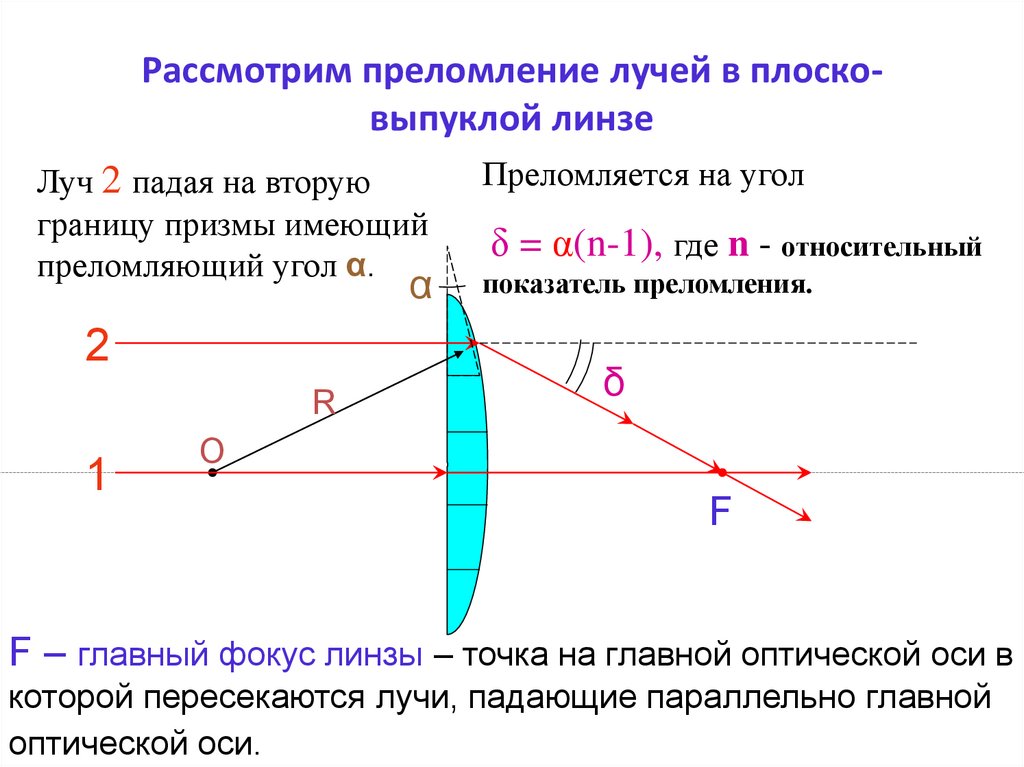
17. Рассмотрим преломление лучей в плоско-выпуклой линзе

Рассмотрим преломление лучей в плосковыпуклой линзе
Луч 2 падая на вторую
границу призмы имеющий
преломляющий угол α.
α
2
R
1
Преломляется на угол
δ = α(n-1), где n - относительный
показатель преломления.
δ
О
F
F – главный фокус линзы – точка на главной оптической оси в
которой пересекаются лучи, падающие параллельно главной
оптической оси.

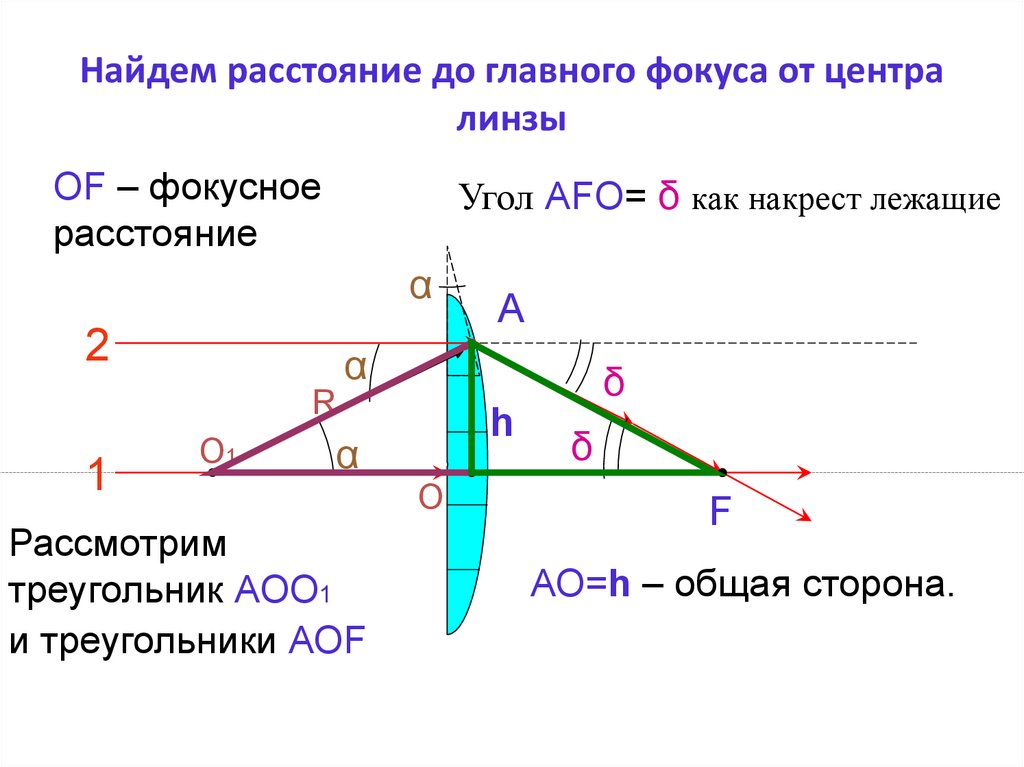
18. Найдем расстояние до главного фокуса от центра линзы

ОF – фокусное
расстояние
Угол АFО= δ как накрест лежащие
α
2
α
δ
R
1
А
О1
h
α
Рассмотрим
треугольник АОО1
и треугольники АОF
О
δ
F
АО=h – общая сторона.

19. Найдем расстояние до главного фокуса от центра линзы

Из треугольника АОО1
h , так как
sin
α
2
R
α малый угол то:
h
sin
R
Из треугольника АOF
h
tg , так как
F
δ малый угол то:
h
tg
F
1
R
О1
α
А
δ
h δ
α
О
Заменим в уравнение
F
(n 1)
углы α и δ на их значения:
h h
(n 1)
1 1
F R
(n 1)
сократим на h: F
R

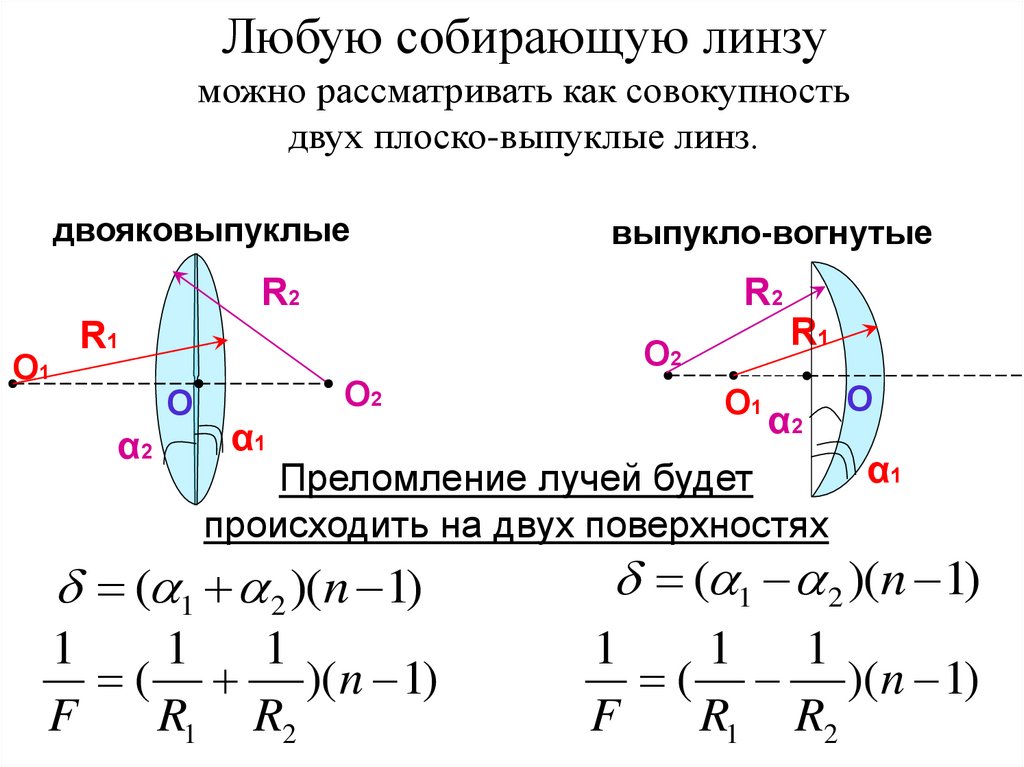
20.

Любую собирающую линзу
можно рассматривать как совокупность
двух плоско-выпуклые линз.
двояковыпуклые
выпукло-вогнутые
R2
R2
O1
R1
O2
O
α2
R1
O2
α1
O1
α2
O
α1
Преломление лучей будет
происходить на двух поверхностях
( 1 2 )(n 1)
( 1 2 )(n 1)
1
1
1
( )( n 1)
F
R1 R2
1
1
1
( )( n 1)
F
R1 R2

21.

22.

23. Оптическая сила линзы

- физическая величина, обратная фокусному
расстоянию.
1
D
F
1
1
D
1дптр
F 1м
Диоптрия - оптическая сила линзы с
фокусным расстоянием 1 метр

24.

1 диоптрия – это оптическая сила линзы, фокусное
расстояние которой 1 метр.
Т.к. у рассеивающей линзы фокус мнимый, то
условились считать её фокусное расстояние
отрицательной величиной. Тогда и оптическая
сила рассеивающей линзы будет отрицательной.
Оптическую силу собирающей линзы условились
считать положительной величиной.

25. Для собирающих линз

D 0
1
1
двояковыпуклые D (
)( n 1) 0 ,так как R1>0
R1 R2
R2>0
плоско-выпуклые
1
D (n 1) 0
R
,так как R>0
1 1
выпукло-вогнутые D (
)( n 1) 0 ,так как |R |>R
R1 R2
2
1

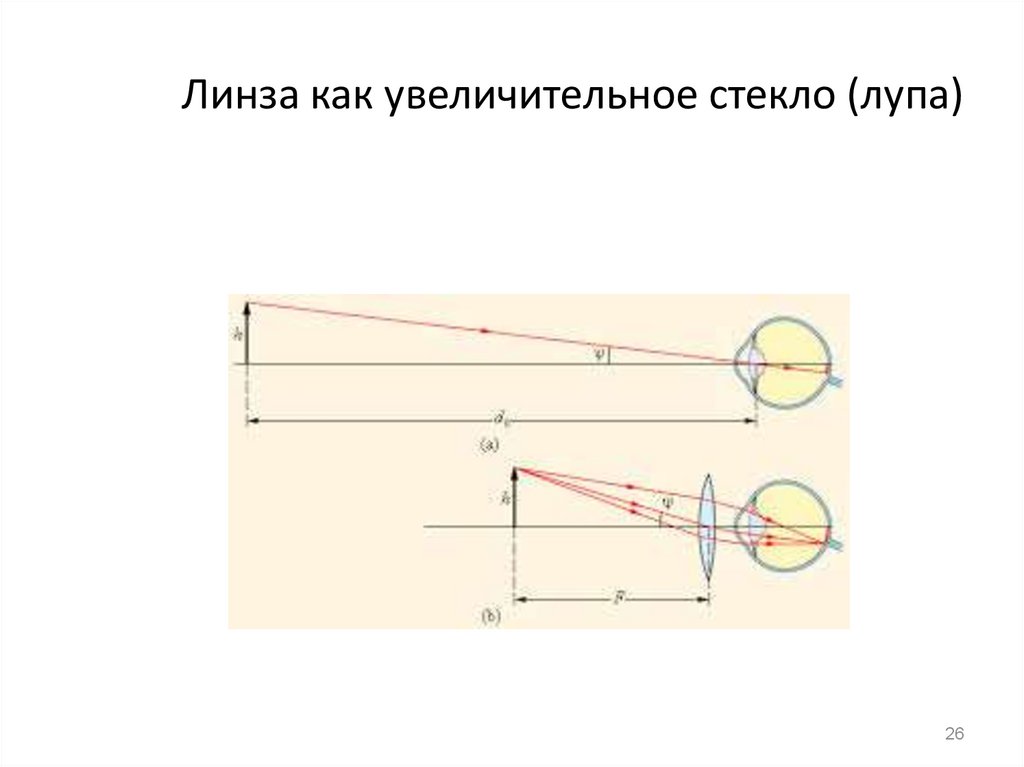
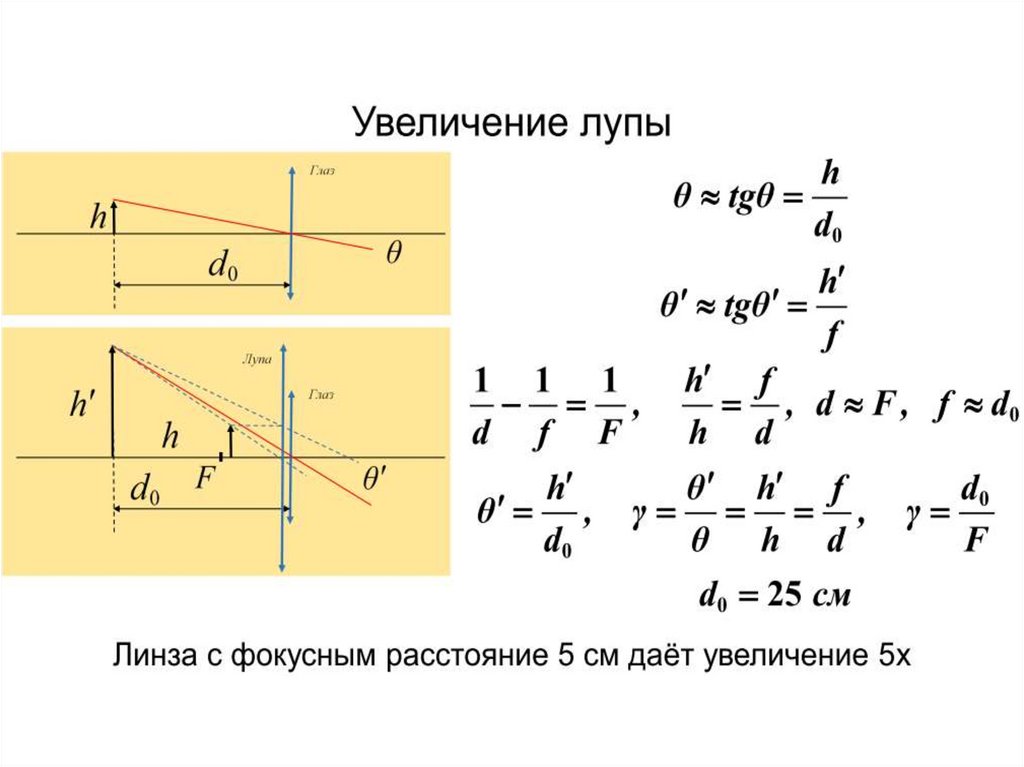
26. Линза как увеличительное стекло (лупа)

26

27.

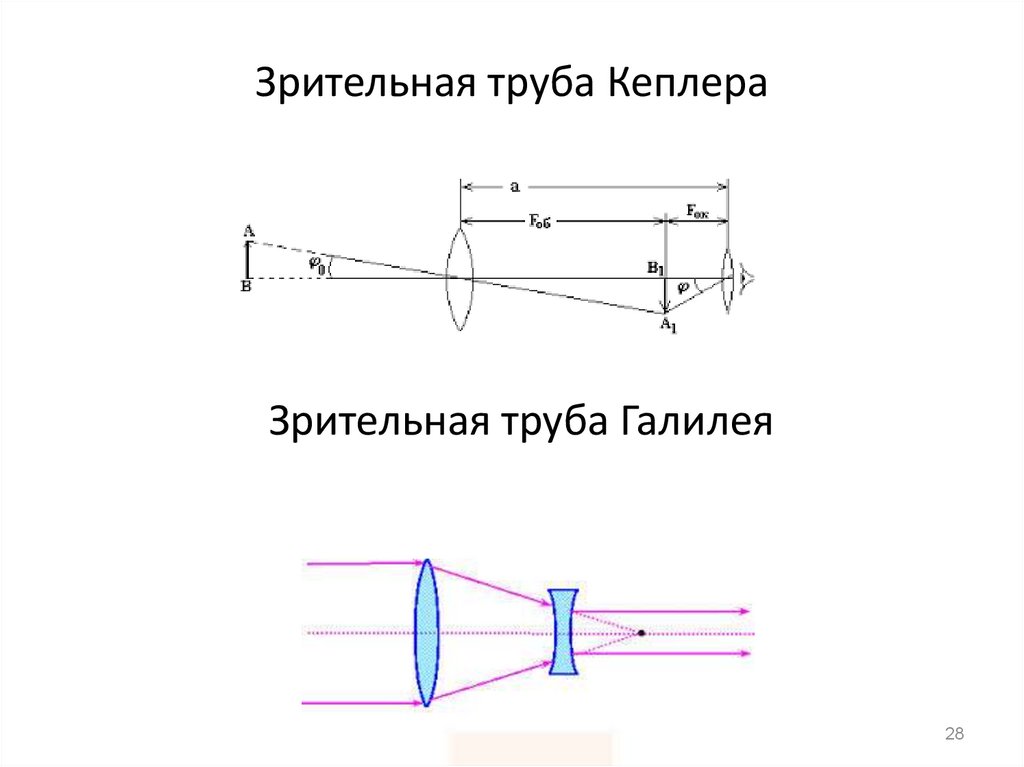
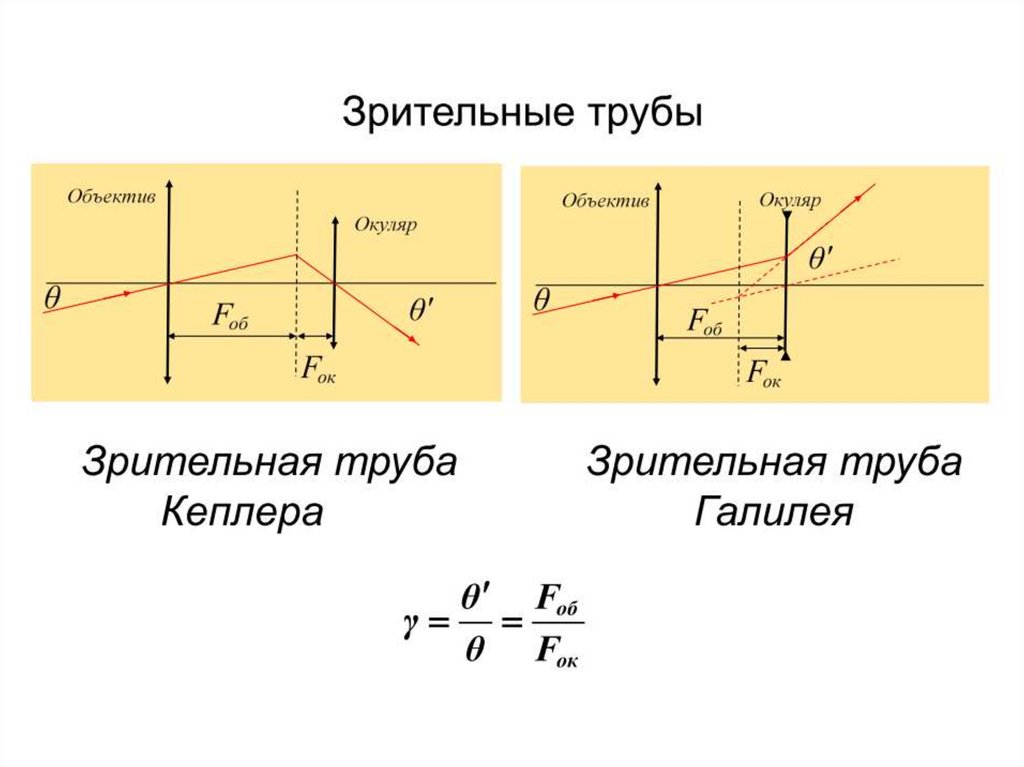
28. Зрительная труба Кеплера

Зрительная труба Галилея
28

29.

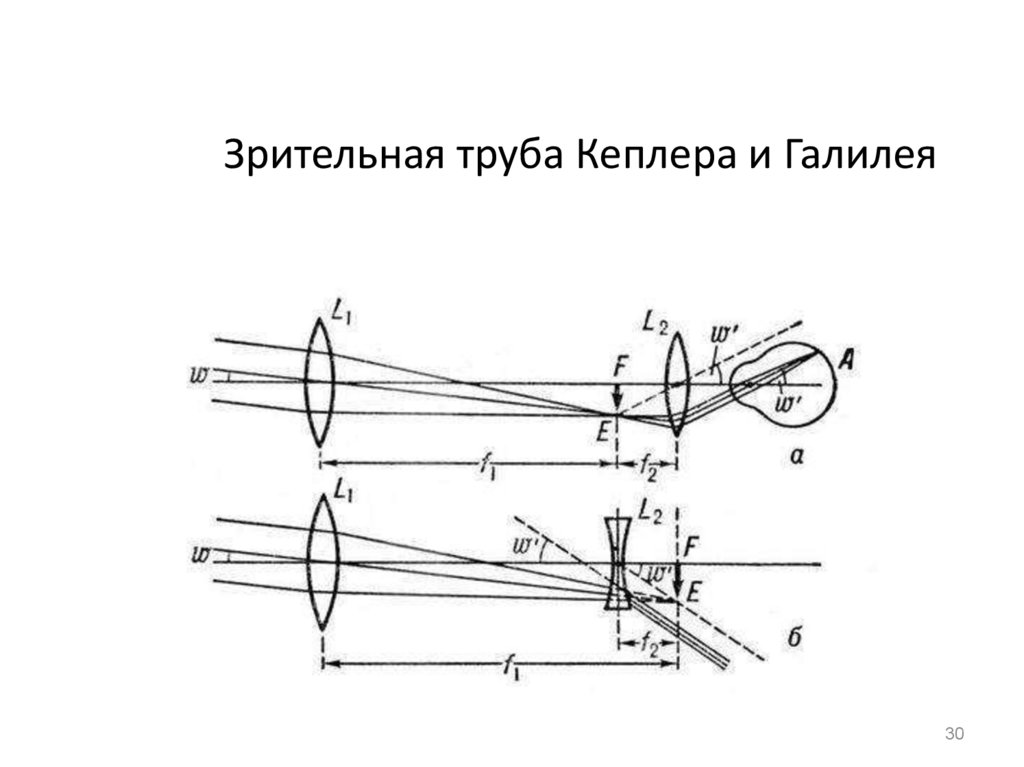
30. Зрительная труба Кеплера и Галилея

30

31. Линза: яркость изображения

Ни один оптический прибор не увеличивает
яркость изображения на сетчатке.
При нормальном увеличении яркость изображения
равна яркости изображения предмета
невооружённым глазом
31

32.

33.

34. Можно ли в телескоп увидеть звёзды днём?

• Звезда – точечный объект, размер
изображения на сетчатке не изменяется;
яркость изображения звезды растёт ~ D2
• Участок неба – объект протяжённый – яркость
изображения на сетчатке не изменяется.
• При определённом диаметре объектива D
изображение звезды станет ярче
изображения неба!
34

35. Импульс электромагнитного поля. Давление света

• Импульс релятивисткой частицы: p = (W/c2)v
• Плотность импульса
электромагнитного поля:
• Давление света:
wv S
1
g 2 2
E H
4 c
c
c
wc I
P cg w
c
c
• Если коэффициент отражения R, то:
• Давление солнечного света:
P (1 R )
I
c
I c 1,5 кВт/м 2
P I / c 5 10 6 Па
35

36.

Аберрации
В идеальной оптической системе все лучи, исходящие из т.А пересекаются
в сопряженной с ней точке А’
В реальной системе или нарушается гомоцентричность пучка и лучи не
имеют общей точки пересечения, или гомоцентричность сохраняется, но
лучи пересекаются в другой точке, не совпадающей с точкой идеального
изображения. Это является следствием аберрации.
Основная задача расчета оптических систем- корректировка
(уменьшение) аберраций.

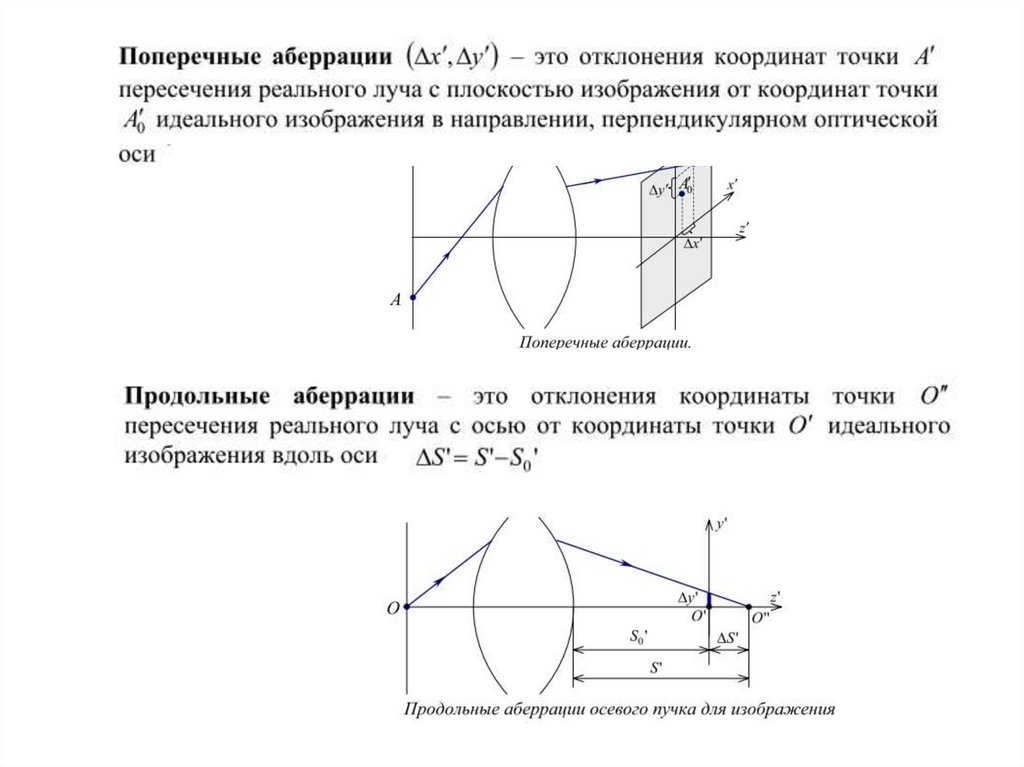
37.

38.

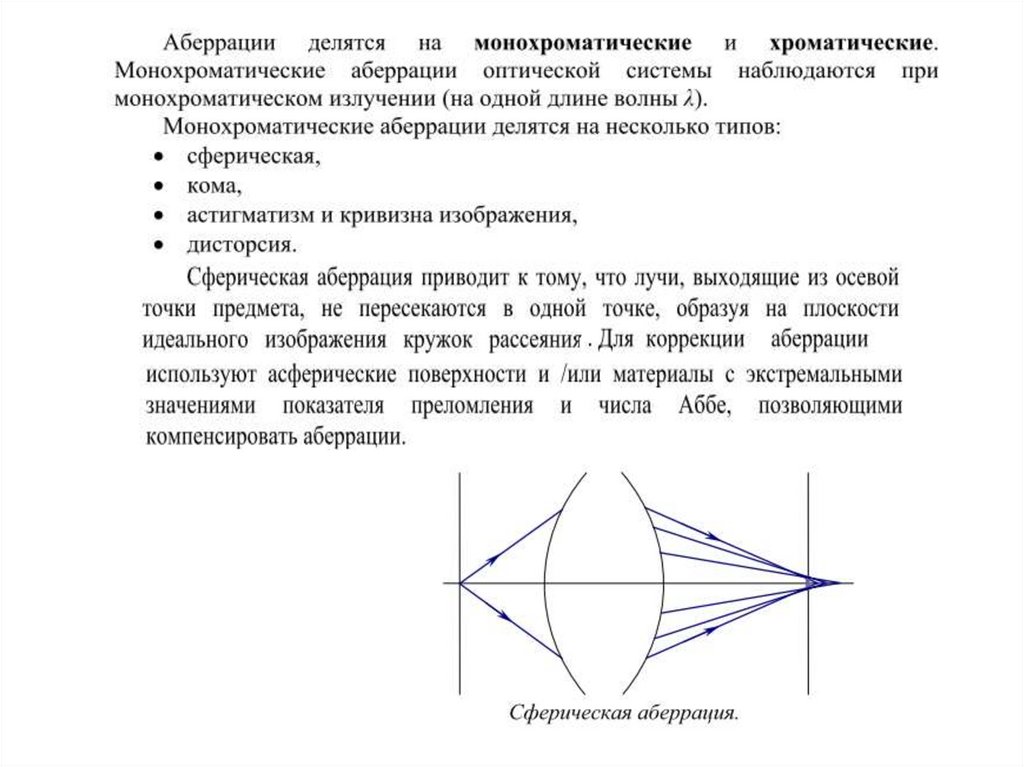
39.

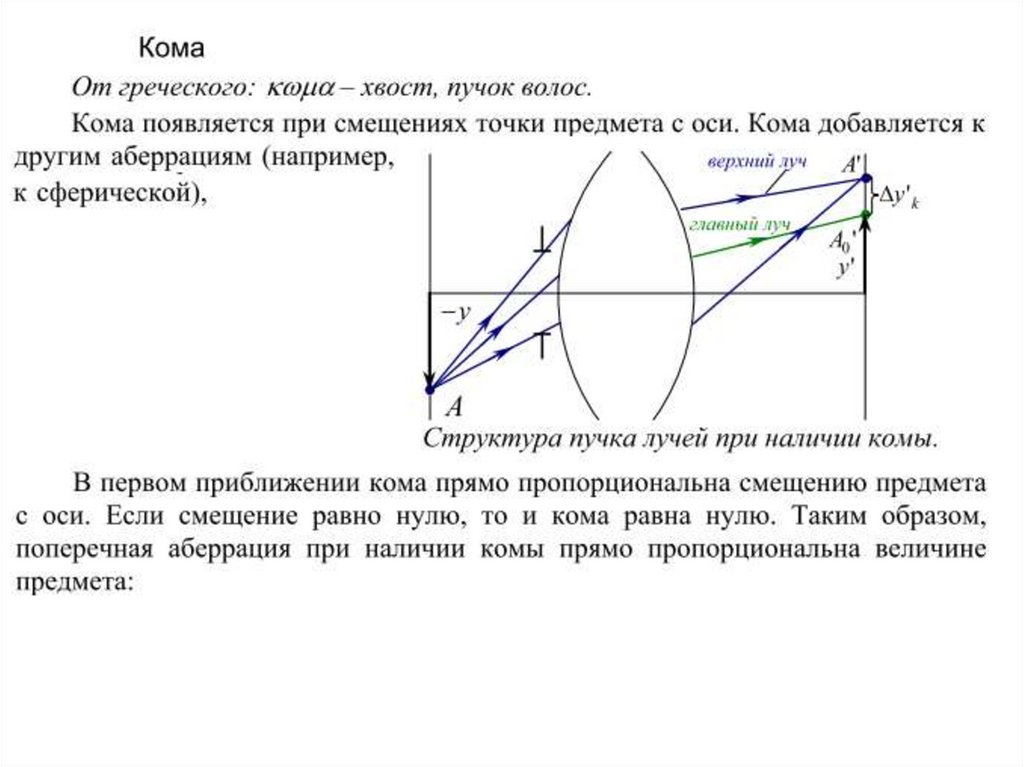
40.

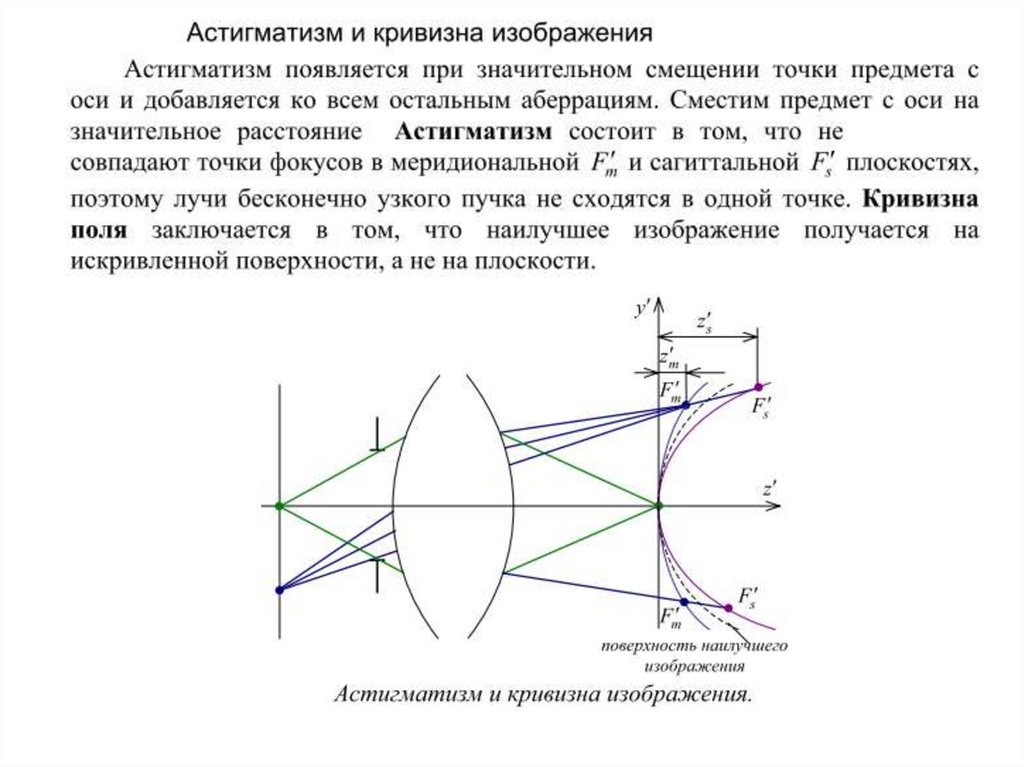
Меридиональная плоскость – это плоскость, проходящая через
оптическую ось (например плоскость рисунка)
Сагиттальная плоскость – это плоскость, которая содержит луч,
перпендикулярный меридиональной плоскости и не проходит
через ось (может быть ломаной и рассматривается по частям). Ее
название произошло от слова “сагитта” (лат.) – стрела. Примером
такой плоскости может служить воображаемая ломаная плоскость,
содержащая луч на рис и перпендикулярная плоскости этого
рисунка.