Similar presentations:
Практикум по решению текстовых задач (для подготовки к ЕГЭ по математике)
1.
(для подготовки к ЕГЭ по математике)Выполнил: Германова Елена Николаевна,
учитель математики
2.
содержание1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Задачи на совместную работу
Задача 1.
Задача 2.
Задача 3.
Задача 4.
Задачи в которых требуется определить время
Задача 5.
Задача 6.
Задача 7.
Заключение
Литература
3.
Задачи на совместную работу.1.Основными компонентами этого типа задач являются:
а) работа;
б) время;
в) производительность труда (работа выполненная в единицу времени).
2. План решения задачи обычно сводится к следующему:
а)принимаем всю работу, которую необходимо выполнить за «1»;
б) находим производительность труда каждого рабочего в отдельности, т.е. 1/t, где t
– время, за которое указанный рабочий может выполнить всю работу, работая
отдельно;
в) находим ту часть всей работы, которую выполняет каждый рабочий отдельно за
то время, которое он работал;
г) составляем уравнение, приравнивая объем всей работы ( т.е. «1») к сумме
слагаемых, каждое из которых есть часть всей работы, выполненная отдельно
каждым из рабочих (если в условии сказано, что при совместной работе всех
рабочих выполнен весь объем работы).
3. Следует отметить, что не всегда в указанных задачах сравнивается
выполненная работа. Основанием для составления уравнения может
служить так же указанное в условии соотношение затраченного времени или
производительности труда.
4.
Задача 1.Две бригады, работая вместе, должны отремонтировать заданный
участок шоссейной дороги за 18 дней.
В действительности же получилось так, что сначала работала только I
бригада, а заканчивала ремонт участка дороги одна II бригада,
производительность труда которой более высокая, чем первой бригады.
В результате ремонт заданного участка дороги продолжался 40 дней.
Причем первая бригада в своё рабочее время выполнила 2/3 всей
работы. За сколько дней был отремонтирован участок дороги каждой
бригадой отдельно?
5.
1.Решение 1- задачи
Пусть вся работа может быть выполнена первой бригадой за «х» дней, а
второй – за «у» дней.
Принимая всю работу за «1», имеем:
1/x – производительность I бригады; 1/y – производительность II бригады;
1/х ×18 – часть работы, которую могла выполнить I бригада за 18 дней.
1/у ×18 – часть работы, которую могла выполнить II бригада за 18 дней.
2. Составим уравнение.
Так как обе бригады, работая совместно, могли выполнить всю работу за 18 дней,
то 1/х ×18 + 1/у × 18 = 1
Первая бригада выполнила 2/3 всей работы, значит она затратила на это 2/3x
дней, а вторая бригада выполнила 1/3 всей работы, значит она затратила на это
1/3у дней.
Так как всего было затрачено 40 дней, то можно составить уравнение: 2/3x + 1/3у
= 40
3.Составим систему уравнений и решим её:
1/х ×18 + 1/у× 18 = 1;
18(х + у) = ху;
2/3x + 1/3у = 40;
2х + у = 120;
у = 120 – 2х;
18(х + 120 – 2х) = х(120 – 2х)
18(120 – х) = 120х – 2х2
2х2 – 120х – 18х + 2160 = 0
х2 – 69х + 1080 = 0
х1 = 45
у1 = 30
х2 = 24
у2 = 72
4.Так как производительность второй бригады была выше, чем первой, то
условию задачи удовлетворяют х = 45 и у = 30.
6.
Задача 2Два мастера, работая вместе, могут выполнить заказ за 6 часов. Если
первый мастер будет работать 9 часов, а потом его сменит второй, то
он закончит работу за 4 часа. За сколько времени может выполнить
заказ каждый из мастеров, работая отдельно?
7.
Решение 2-й задачиА – работа; k – производительность; t – время.
А
k
t
совместная работа
1
1/6
6 ч.
I мастер
9х
х
9 ч.
II мастер
4у
y
4 ч.
Составим систему:
х + у = 1/6
9х + 4у = 1
t1 = А/k = 1/1/15 = 15 ч.;
Ответ: 15 ч. и 10 ч.
t2 = 10 ч.
х = 1/5
у = 1/10
8.
Задача 3Машинистка начала перепечатывать рукопись, через 4 часа к ней
присоединилась вторая машинистка. Проработав 8 часов, они
закончили перепечатку всей рукописи. За сколько часов каждая может
перепечатать всю рукопись, если первой на это требуется на 8 часов
больше, чем второй?
Анализ: Процесс работы, описанный в задаче, характеризуется тремя
величинами: объемом работы, временем работы и
производительностью труда.
9.
Решение 3-й задачиПримем объем работы за «1».
Примем время, необходимое второй машинистке для перепечатывания
всей рукописи, за t (t › 0). Тогда её производительность равна 1/t стр/ч.
Время, необходимое первой машинистке на всю работу, будет на 4 часа
больше, т.е. (t + 4) часа, и её производительность равна 1/t + 4 стр/ч.
Первая машинистка работала (4 + 4) часа, а вторая только 4 часа. (По
условию к первой машинистке присоединяется вторая, значит весь
процесс работы начался раньше, и 8 часов – это время работы первой
машинистки). Получаем уравнение:
8 ×1/(t + 8) + 4×1/t = 1
Преобразовав данное уравнение при t(t + 8) ≠ 0
t2 – 4t – 32 = 0
t1 = 8
t2 = - 4
- 4< 0 не соответствует смыслу задачи.
Следовательно, вторая машинистка затратила на перепечатку рукописи 8
часов, а первая, соответственно 16 часов.
Ответ: 16 ч. и 8 ч.
10.
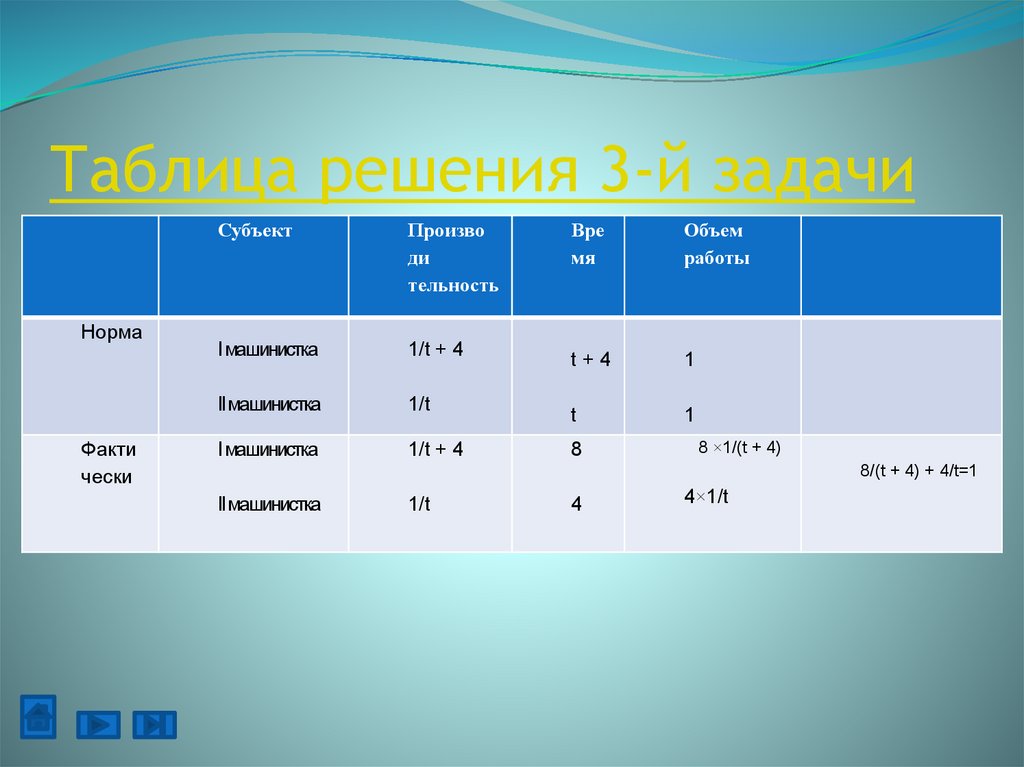
Таблица решения 3-й задачиНорма
Факти
чески
Субъект
Произво
ди
тельность
I машинистка
1/t + 4
IIмашинистка
1/t
I машинистка
1/t + 4
Вре
мя
Объем
работы
t+4
1
t
1
8
8 ×1/(t + 4)
8/(t + 4) + 4/t=1
IIмашинистка
1/t
4
4×1/t
11.
ЗАДАЧА 4Два подъемных крана, работая вместе,
разгрузили баржу за 6 часов. За какое время
может разгрузить баржу каждый кран, работая
отдельно, если один из них может разгрузить её
на 5 часов скорее, чем другой?
12.
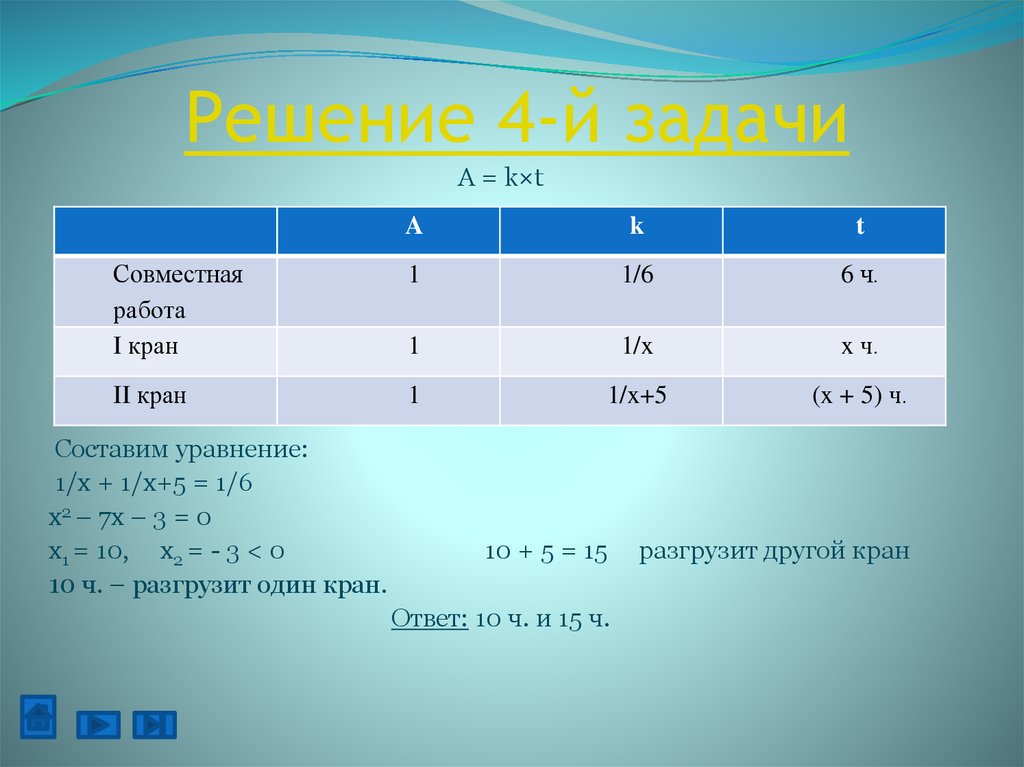
Решение 4-й задачиА = k×t
A
k
t
Совместная
работа
I кран
1
1/6
6 ч.
1
1/x
x ч.
II кран
1
1/x+5
(x + 5) ч.
Составим уравнение:
1/x + 1/x+5 = 1/6
x2 – 7x – 3 = 0
x1 = 10, x2 = - 3 < 0
10 ч. – разгрузит один кран.
10 + 5 = 15
Ответ: 10 ч. и 15 ч.
разгрузит другой кран
13.
Задача 5Планом было предусмотрено, что предприятие на протяжении
нескольких месяцев изготовит 6000 насосов. Увеличив
производительность труда, предприятие стало изготавливать в
месяц на 70 насосов больше, чем было предусмотрено, и на один
месяц раньше установленного срока перевыполнило задание на
30 насосов. На протяжении скольких месяцев было
предусмотрено выпустить 6000 насосов?
14.
Решение 5-й задачиПусть за «х» месяцев было предусмотрено выполнение планового
задания. Тогда за (х – 1) месяцев было выпущено 6030 насосов. В месяц
по плану предприятие должно было выпускать 6000/x насосов, а
фактически выпустило в месяц 6030/x – 1 насосов.
Из условия задачи следует уравнение:
6030/(x – 1) - 6000/x = 70
7х2 – 10х – 600 = 0
х1 = 10
х2 = - 60/7 ( не удовлетворяет условию задачи)
Ответ: 10 месяцев.
15.
Задача 6Две трубы наполняют бассейн за 3 часа. Одна
первая труба может наполнить бассейн на 2,5 часа
быстрее, чем одна вторая труба. За сколько часов
может наполнить бассейн одна первая труба?
16.
Решение6-й
задачи
Пусть первая труба заполнит бассейн за «х» часов, а вторая – за
«у» часов. Примем вместительность бассейна за «1». Тогда за 1
час первая труба заполняет 1/x часть бассейна, а вторая - 1/у.
Вместе обе трубы за 1 час заполняют (1/x + 1/у) часть бассейна.
По условию первая труба заполняет бассейн нам 2,5 часа
быстрее, отсюда у = х + 2,5
За 1 час обе
трубы заполняют 1/3 часть бассейна, тогда 1/x + 1/у = 1/3
Составим систему уравнений:
у = х + 2,5
1/x + 1/у = 1/3
у = х + 2,5
3(х + у) = ху
2х2 – 7х – 15 = 0
х1 = 5
х2 = - 3/2 (по смыслу задачи х >0)
Ответ: 5 часов.
17.
Задача 7Из трех труб, открытых одновременно бассейн
наполняется за 3 часа 45 минут. Одна первая труба
наполняет бассейн в 2,6 раза быстрее, чем вторая
труба, а та наполняет бассейн на 3 часа медленнее,
чем третья. За сколько часов наполняет бассейн
третья труба?
18.
Анализ 7-й задачиВ этой задаче «работают» три участника,
используются понятия «быстрее» и «медленнее».
Необходимо перевести их на язык «больше –
меньше».
Получаем: «Время, необходимое первой трубе, в
2,6 раз меньше, чем время, необходимое второй
трубе».
«Время работы второй трубы на 3 часа больше, чем
время работы третьей трубы».
19.
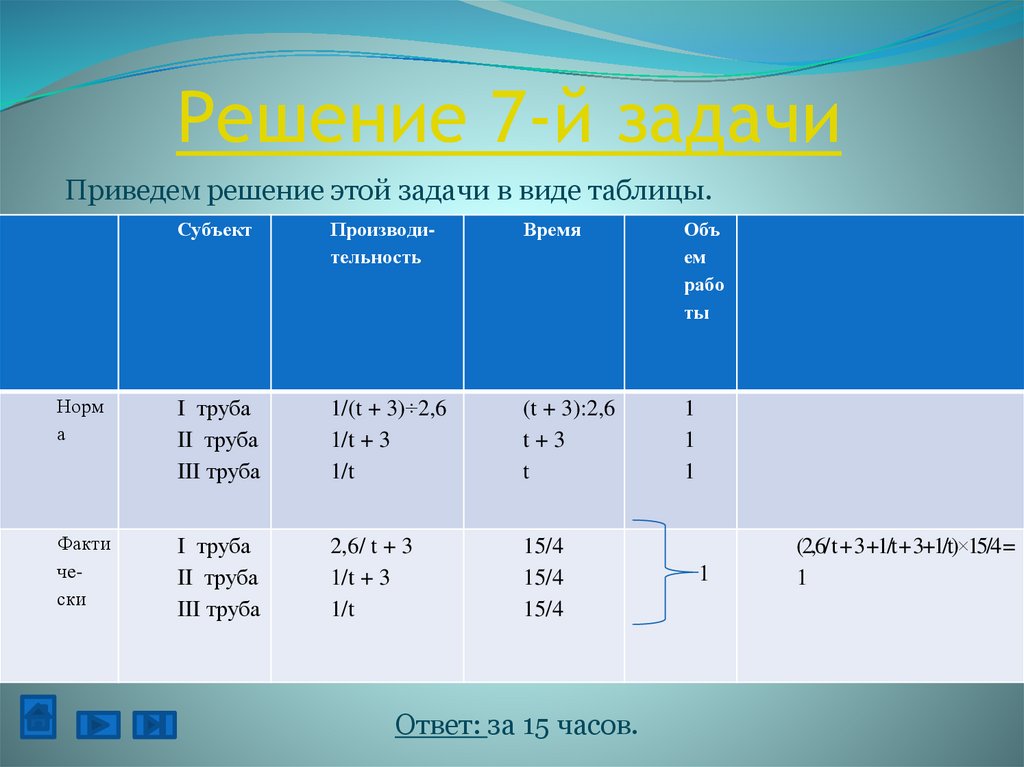
Решение 7-й задачиПриведем решение этой задачи в виде таблицы.
Субъект
Производительность
Время
Объ
ем
рабо
ты
Норм
а
I труба
II труба
III труба
1/(t + 3)÷2,6
1/t + 3
1/t
(t + 3):2,6
t+3
t
1
1
1
Факти
чески
I труба
II труба
III труба
2,6/ t + 3
1/t + 3
1/t
15/4
15/4
15/4
Ответ: за 15 часов.
1
(2,6/ t+ 3 +1/t+ 3+1/t)×15/4 =
1
20.
ЗаключениеПриведенные рассуждения не обязательны для записи во время
экзамена. Они являются своеобразным конспектом, который
поможет в конкретной ситуации при решении подобных задач.
Как известно текстовые задачи относятся ко 2 части ЕГЭ. Их
решение не вносится в чистовик, и оформление решения не
проверяется. Поэтому для себя обычно достаточно сделать лишь
некоторые пометки. Здесь рекомендуется составлять таблицы, в
которых заносятся данные величины, а так же выражения,
возникающие по ходу рассуждений.
21.
Литература1.Лаппо Л.Д., Попов М.А. Математика ЕГЭ. Эффективная подготовка. Издательство
«Экзамен». Москва 2008.
2. ЕГЭ 2007. Математика Реальные тесты и ответы. Фолио.
3. Математика ЕГЭ-2008. Вступительные испытания. Под. Ред. Ф.Ф. Лысенко
Издательство «Легион». Ростов-на-Дону 2008.
4. Садовничий Ю.В. Алгебра. Конкурсные задачи с решениями. Учебное пособие.
Издательство«Экзамен». Москва 2007.
5. Математика. Готовимся к ЕГЭ. Тренировочные тематические задания
повышенной сложности. Составители: Г.И. Ковалева и др. Издательство
«Учитель» Волгоград 2008.
6. Математика. Готовимся к ЕГЭ. Решение задач и выполнение заданий с
комментариями и ответами. Составители: В.Н. Студенецкая, З.С. Гребнева
Издательство «Учитель» Волгоград 2007.
7. Математика 11 класс. ЕГЭ. Составитель М.Б. Буданцева. Издательство Творческий
центр. Сфера. Москва 2007.



















 mathematics
mathematics








