Общая теория связи

1.

2.

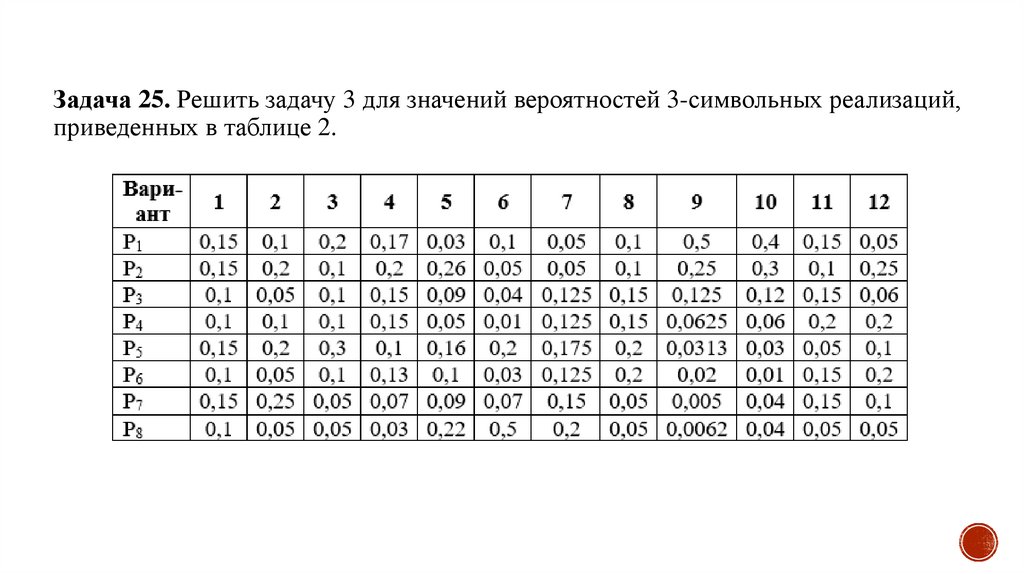
3.

Помехоустойчивое кодирование – теоретический доклад.
Коды Рида-Соломона – теоретический доклад.
Симантические коды – теоретический доклад.
Решение практических задач по данной тематике.
Основная литература
1.
Андреев Р.Н., Краснов Р.П., Чепелев М.Ю. Теория электрической связи: курс лекций. Учебное пособие
для вузов. – М.: Изд-во «Горячая линия – Телеком», 2014 г.
2.
Васин В.А., Калмыков В.В., Себекин Ю.Н., Сенин А.И., Федоров И.Б. Радиосистемы передачи
информации. Учебное пособие для вузов / Под ред. И.Б. Федорова и В.В. Калмыкова. – М.: Изд-во
«Горячая линия – Телеком», 2015 г.

4.

Дополнительная литература
1.
Теория электрической связи: учебное пособие / К.К. Васильев, В.А. Глушков, А.В. Дормидонтов, А.Г. Нестеренко; под общ. ред.
К.К. Васильева. – Ульяновск: УлГТУ, 2008. – 452 с.
2.
Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом
«Вильямс», 2003. – 1104 с.
3.
Каганов В.И., Битюков В.К. Основы радиоэлектроники и связи: Учеб. пособие для вузов. – М.: Горячая линия-Телеком, 2007. –
542 с.
4.
Стеценко О.А. Радиотехнические цепи и сигналы: Учебник. – М.: Высш. шк., 2007. – 432 с.
5.
Периодические издания: журнал «Вестник»; «Вестник связи»; «Автоматика, Связь, Информатика».
6.
Основы теории электрической связи. Учеб. Пособие/ под ред. А.Н. Путилина.- СПб.: ВАС, 1997.- 155 с.
7.
Прокис Дж. Цифровая связь.- М.: Радио и связь, 2000,- 797 с.
8.
Электросвязь. Введение в специальность: Учеб. пособие для вузов/ В.Г. Дурнев, А.Ф. Зелевич, Б.И. Крук и др.- М.: Радио и
связь, 1988.-240 с.

5.

6.

Рассмотрим простые практические способы построения кодов, способных
обнаруживать и исправлять ошибки. Ограничимся рассмотрением двоичных
каналов и равномерных кодов.

7.

Это простой способ обнаружения некоторых из возможных ошибок.
Будем использовать в качестве разрешенных половину возможных
кодовых комбинаций, а именно те из них, которые имеют четное число
единиц (или нулей). Однократная ошибка при передаче через канал
неизбежно приведет к нарушению четности, что и будет обнаружено на
выходе канала. Очевидно, что трехкратные, пятикратные и вообще
ошибки нечетной кратности ведут к нарушению четности и
обнаруживаются этим методом, в то время как двукратные,
четырехкратные и вообще ошибки четной кратности – нет.

8.

Практическая техника кодирования методом контроля четности
следующая. Из последовательности символов, подлежащих передаче
через канал, выбирается очередной блок из k-1символов, называемых
информационными, и к нему добавляется k-й символ, называемый
контрольным. Значение контрольного символа выбирается так, чтобы
обеспечить четность получаемого кодового слова, т.е. чтобы сделать его
разрешенным.
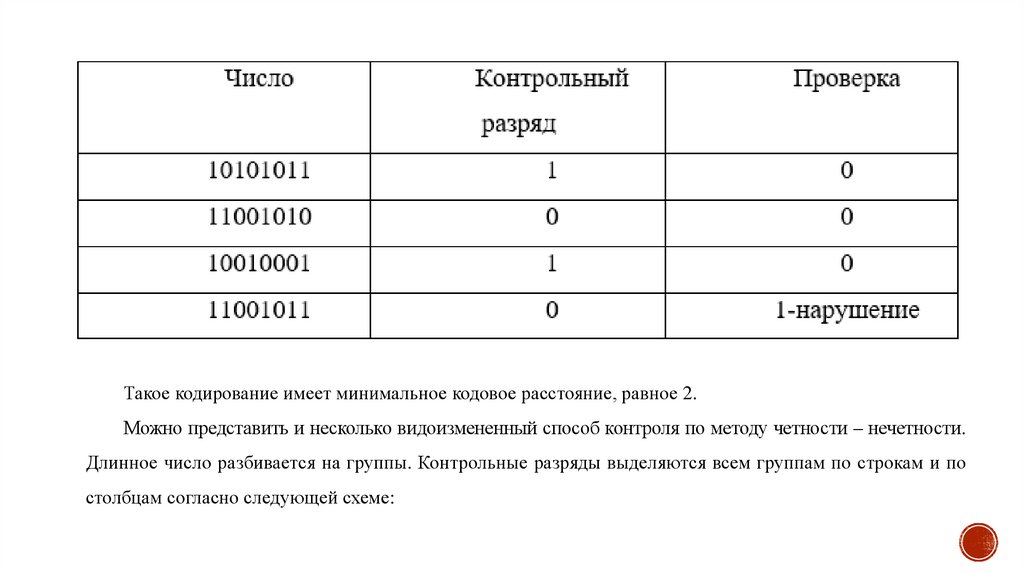
Метод контроля четности представляет значительную ценность и широко
применяется в тех случаях, в которых вероятность появления более одной
ошибки пренебрежимо мала (во многих случаях, если наверняка знать,
что кодовое слово принято с ошибкой, имеется возможность запросить
повторную передачу). В то же время избыточность кода увеличивается
минимально и незначительно при больших k(в k/( k-1)раз).

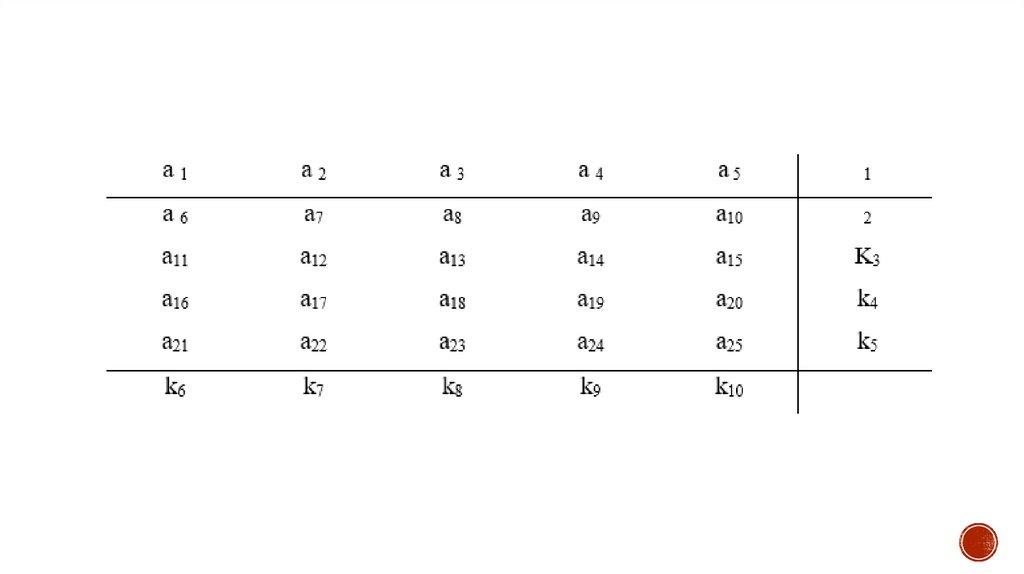
9.

Рассмотренный выше метод контроля четности может быть применен многократно для
различных комбинаций разрядов передаваемых кодовых слов – и это позволит не только
обнаруживать, но и исправлять определенные ошибки.
Пример:
Будем из входной последовательности символов брать по четыре информационных
символа а1а2а3а4, дополнять их тремя контрольными символами а5а6а7 и получившееся
семисимвольное слово посылать в канал. Контрольные символы будем подбирать так,
чтобы были четными следующие суммы:

10.

В каждую сумму входит по оному контрольному символу, поэтому данное
требование всегда выполнимо.
Благодаря «маленьким хитростям», предусмотренным при формировании
контрольных сумм, проверка их четности на выходе канала позволяет
однозначно установить, была ли допущена при передаче однократная
ошибка и какой из разрядов был при этом искажен (ошибками большей
кратности пренебрегаем).Действительно, если один из семи символов
был искажен, то по крайней мере одна из сумм обязательно окажется
нечетной, т.е. четность всех контрольных сумм s1, s2, s3 свидетельствует
об отсутствии однократных ошибок.

11.

Далее, лишь одна сумма будет нечетной в том, (и только в том) случае,
если искажен входящий в эту сумму один из трех контрольных символов
(a5, a6 или a7). Нечетность двух или трех сумм означает, что искажен тот
из информационных символов а2, а3 или а4, который входи в обе эти
суммы. Наконец, нечетность всех трех сумм означает, что неверно принят
входящий во все суммы символ а1.
Итак, в данном примере метод контрольных сумм, увеличивая длину кода
в 7/4=1,75 раза за счет введения избыточности, позволяет исправить
любую однократную ошибку (но не ошибку большей кратности).
Основываясь на этой идее, в принципе, можно построить коды,
исправляющие все ошибки большей (но всегда ограниченной) кратности.

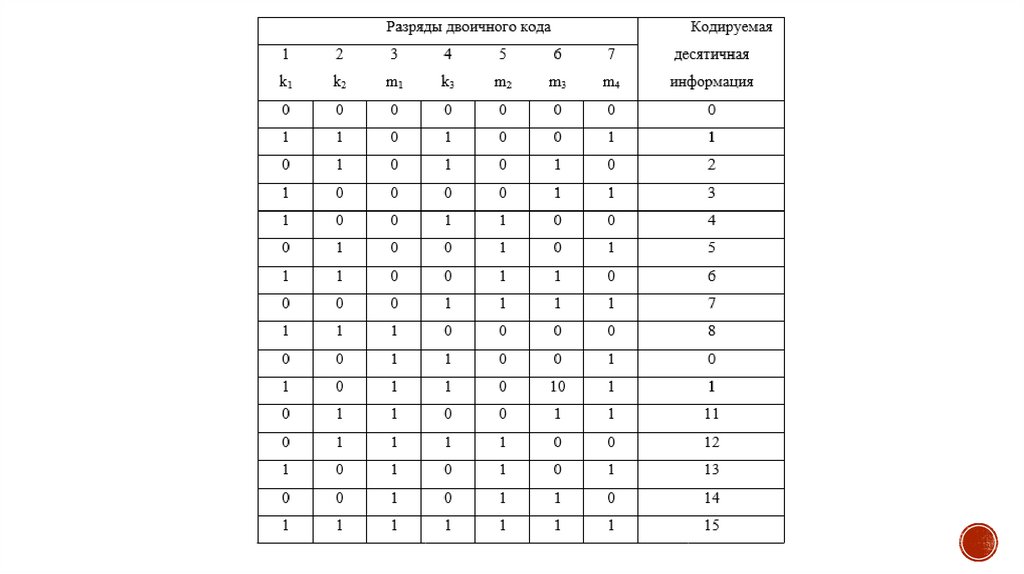
12.

Как уже указывалось, функции контроля можно осуществить при
информационной избыточности. Такая возможность появляется при
использовании специальных методов кодирования информации. В самом
деле, некоторые методы кодирования информации допускают наличие
разрешенных и запрещенных комбинаций. В качестве примера можно
привести двоично-десятичные системы представления числовой
информации (Д-коды). Появление запрещенных комбинаций для
подобного представления свидетельствует об ошибке в результатах
решения задачи. Такой метод можно использовать для контроля
десятичных операций. Однако он является частным примером и не
решает общей задачи.

13.

Задача кодирования информации представляется как некоторое
преобразование числовых данных в заданной программе счисления. В
частном случае эта операция может быть сведена к группированию
символов (представление в виде триад и тетрад) или представлению в
виде символов позиционной системы счисления. Так как любая
позиционная система счисления не несет в себе избыточности
информации, и все кодовые комбинации являются разрешенными, то
использовать такие системы для контроля не представляется возможным.
Систематический код – код, содержащий в себе кроме информационных
контрольные разряды.

14.

В контрольные разряды записывается некоторая информация об исходном числе.
Поэтому можно говорить, что систематический код обладает избыточностью.
При этом абсолютная избыточность будет выражаться количеством контрольных
разрядов k, а относительная избыточность – отношением k/n, где n=m+k –
общее количество разрядов в кодовом слове (m – количество информационных
разрядов).
Понятие корректирующей способности кода обычно связывают с возможностью
с возможностью обнаружения и исправления ошибки. Количественно
корректирующая способность кода определяется вероятностью обнаружения
или исправления ошибки. Если имеем n- разрядный код и вероятность
искажения одного символа будет P, то вероятность того, что искажены k
символов, а остальные n-k символов не искажены, по теореме умножения
вероятностей будет

15.

Число кодовых комбинаций, каждая из которых содержит k искаженных элементов,
равна числу сочетаний из n по k:
Тогда вероятность искажения
Так как на практике P=10-3÷10-4, наибольший вес в сумме вероятностей имеет
вероятность искажения одного символа. Следовательно, основное внимание нужно
обратить на обнаружение и исправление одиночной ошибки.
Корректирующая способность кода связана также с понятием кодового расстояния.

16.

Кодовое расстояние d(A,B) кодовых комбинаций А и В определяется как вес
такой третьей кодовой комбинации, которая получается сложением исходных
комбинаций по модулю 2.
Вес кодовой комбинации V(A) – количество единиц, содержащихся в кодовой
комбинации.
Коды можно рассматривать и как некоторые геометрические (пространственные)
фигуры. Например, триаду можно представить в виде единичного куба,
имеющего координаты вершин, которые отвечают двоичным символам (рис. 1) в
этом случае кодовое расстояние воспринимается как сумма длин ребер между
соответствующими вершинами куба (принято, что длина одного ребра равна 1).
Оказывается, что любая позиционная система отличается тем свойством, что
минимальное кодовое расстояние равно 1.

17.

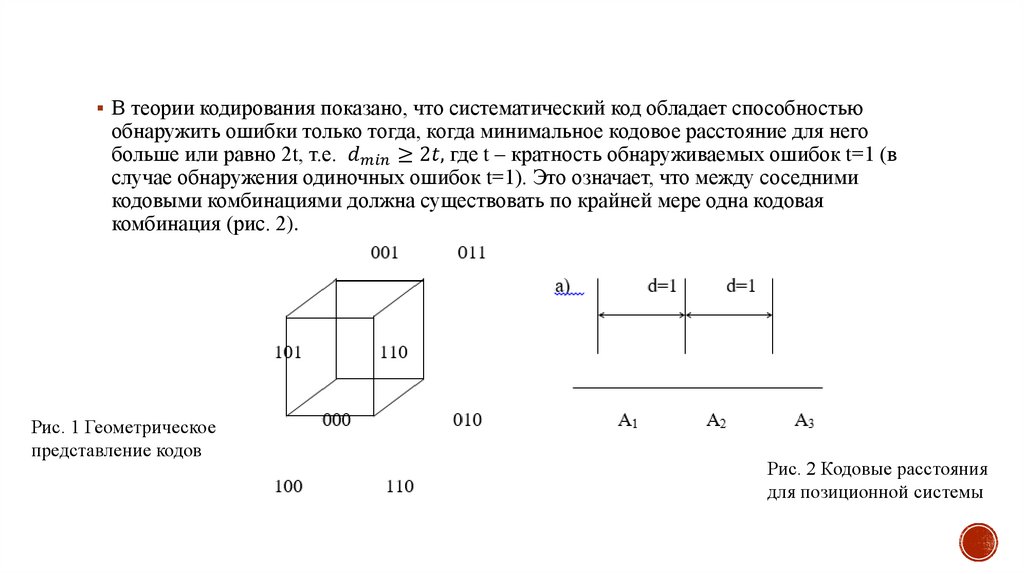
В теории кодирования показано, что систематический код обладает способностью
обнаружить ошибки только тогда, когда минимальное кодовое расстояние для него
больше или равно 2t, т.е.