Similar presentations:
Осевая и центральная симметрия
1.
Осевая и центральнаясимметрия
8 класс
Учитель: Вагина Наталия Владимировна,
учитель математики ГБОУ СОШ №307
Адмиралтейского района Санкт-Петербурга
2.
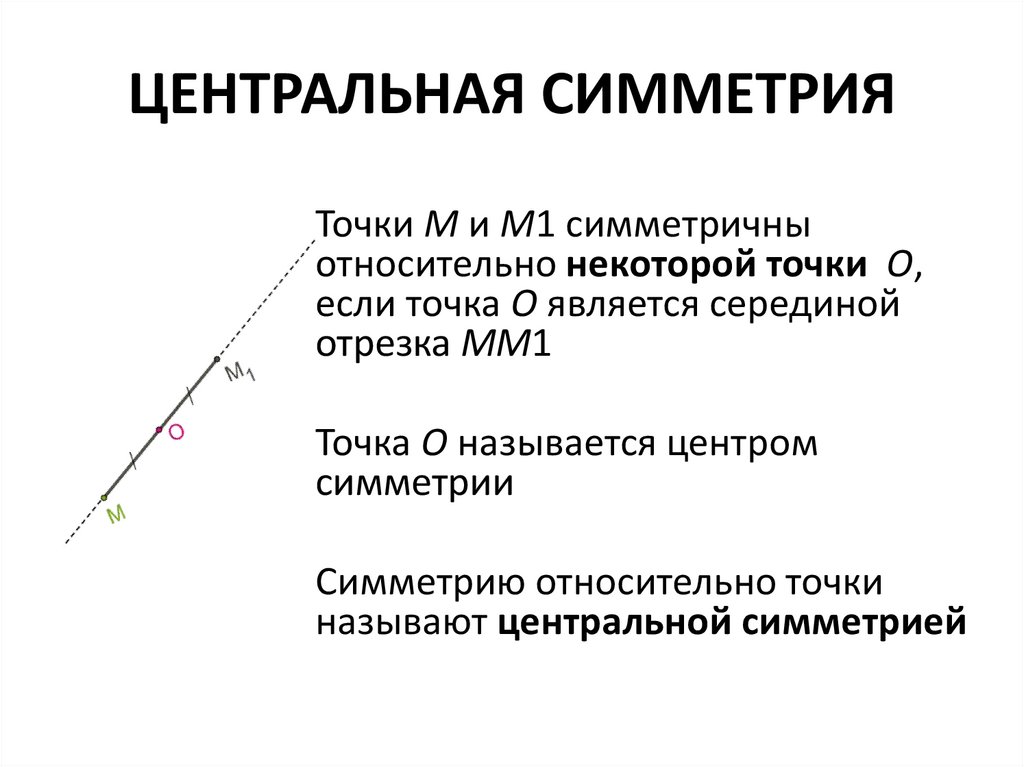
ЦЕНТРАЛЬНАЯ СИММЕТРИЯТочки M и M1 симметричны
относительно некоторой точки O,
если точка O является серединой
отрезка MM1
Точка O называется центром
симметрии
Симметрию относительно точки
называют центральной симметрией
3.
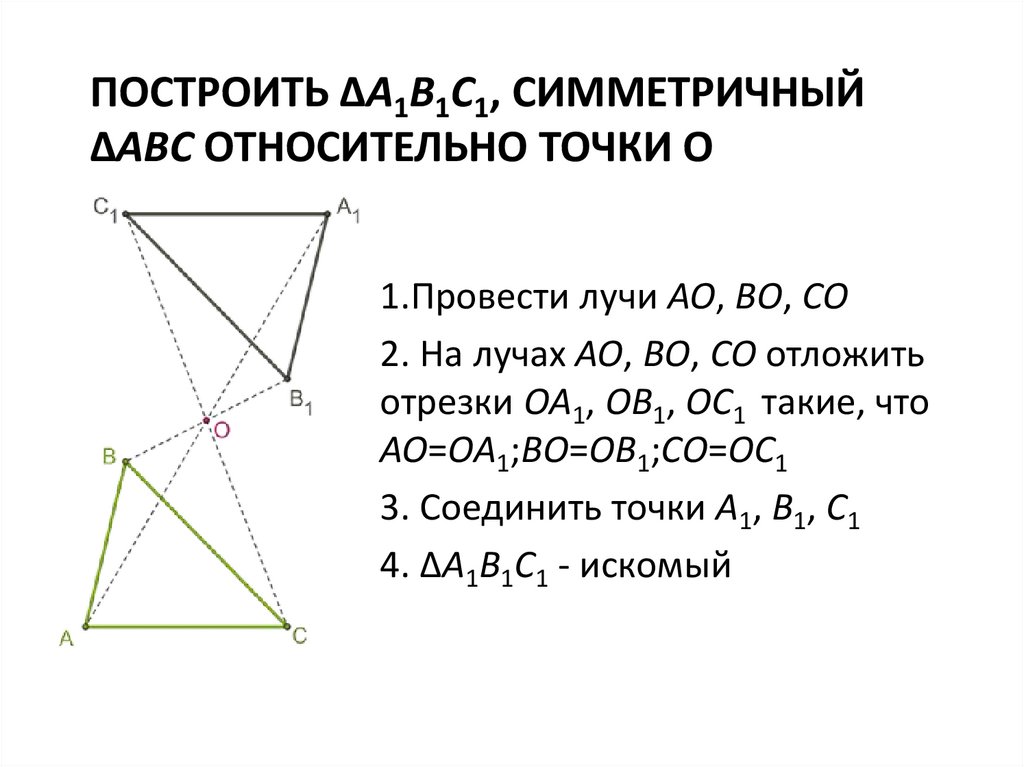
ПОСТРОИТЬ ΔA1B1C1, СИММЕТРИЧНЫЙΔABC ОТНОСИТЕЛЬНО ТОЧКИ O
1.Провести лучи AO, BO, CO
2. На лучах AO, BO, CO отложить
отрезки OA1, OB1, OC1 такие, что
AO=OA1;BO=OB1;CO=OC1
3. Соединить точки A1, B1, C1
4. ΔA1B1C1 - искомый
4.
Фигуры, симметричные относительнонекоторой точки, равны
Определение:
Фигура называется симметричной относительно
точки, если для каждой этой точки фигуры
симметричная ей точка также лежит на этой фигуре.
5.
Примеры центральной симметрии6.
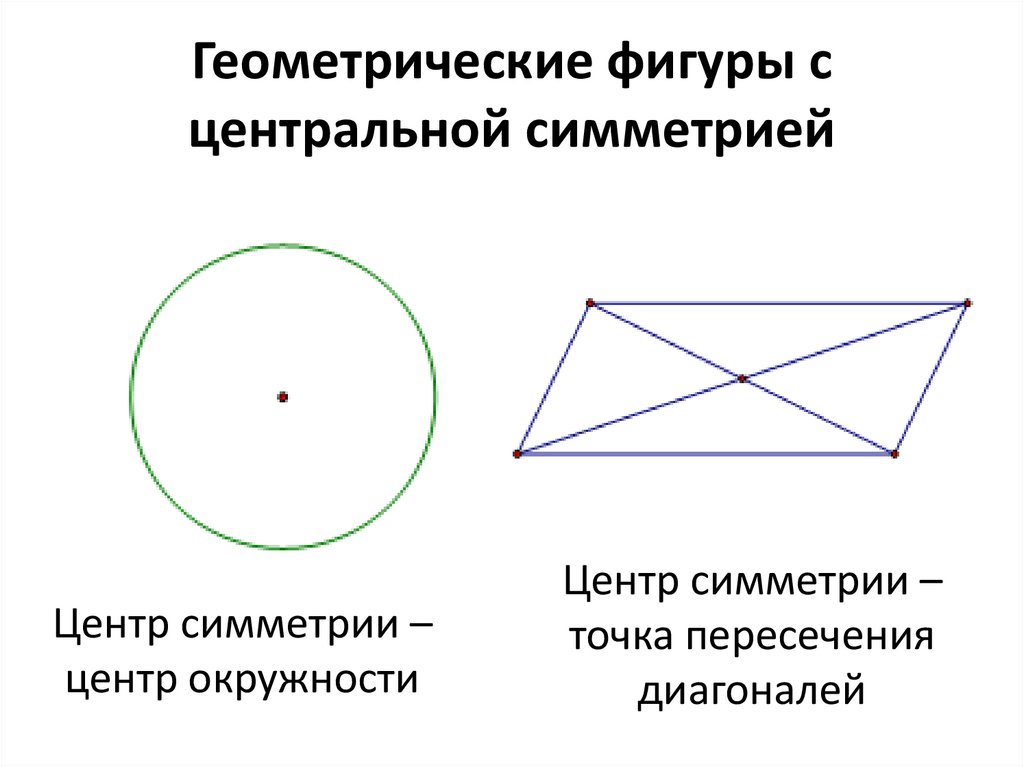
Геометрические фигуры сцентральной симметрией
Центр симметрии –
центр окружности
Центр симметрии –
точка пересечения
диагоналей
7.
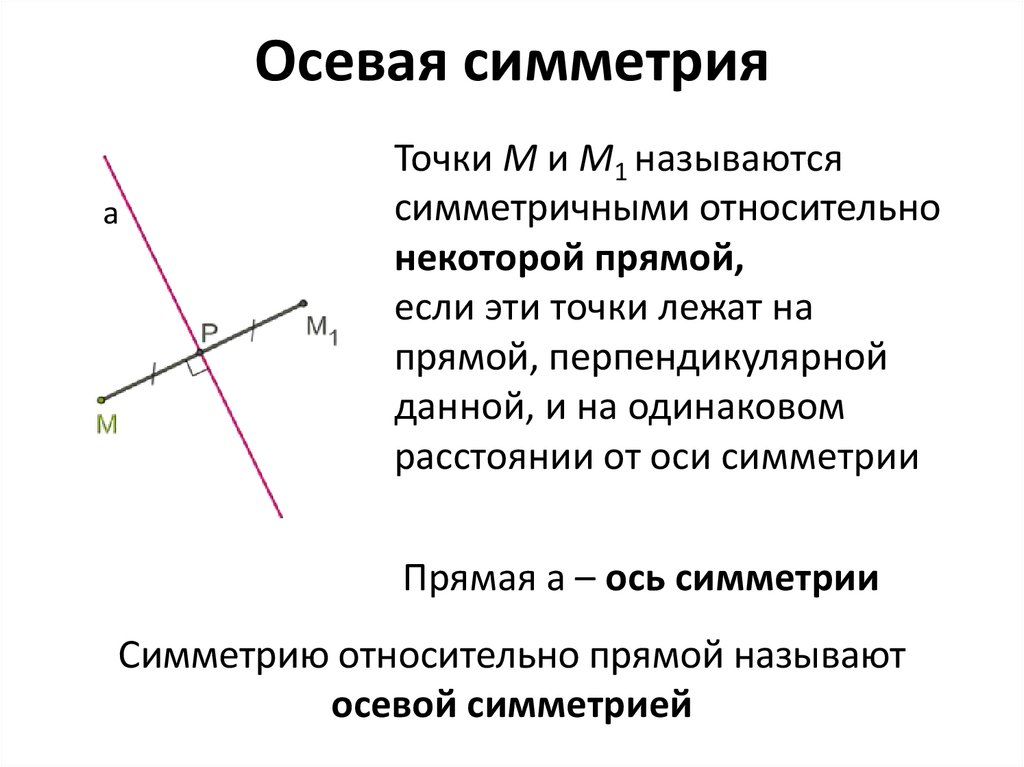
Осевая симметрияa
Точки M и M1 называются
симметричными относительно
некоторой прямой,
если эти точки лежат на
прямой, перпендикулярной
данной, и на одинаковом
расстоянии от оси симметрии
Прямая а – ось симметрии
Симметрию относительно прямой называют
осевой симметрией
8.
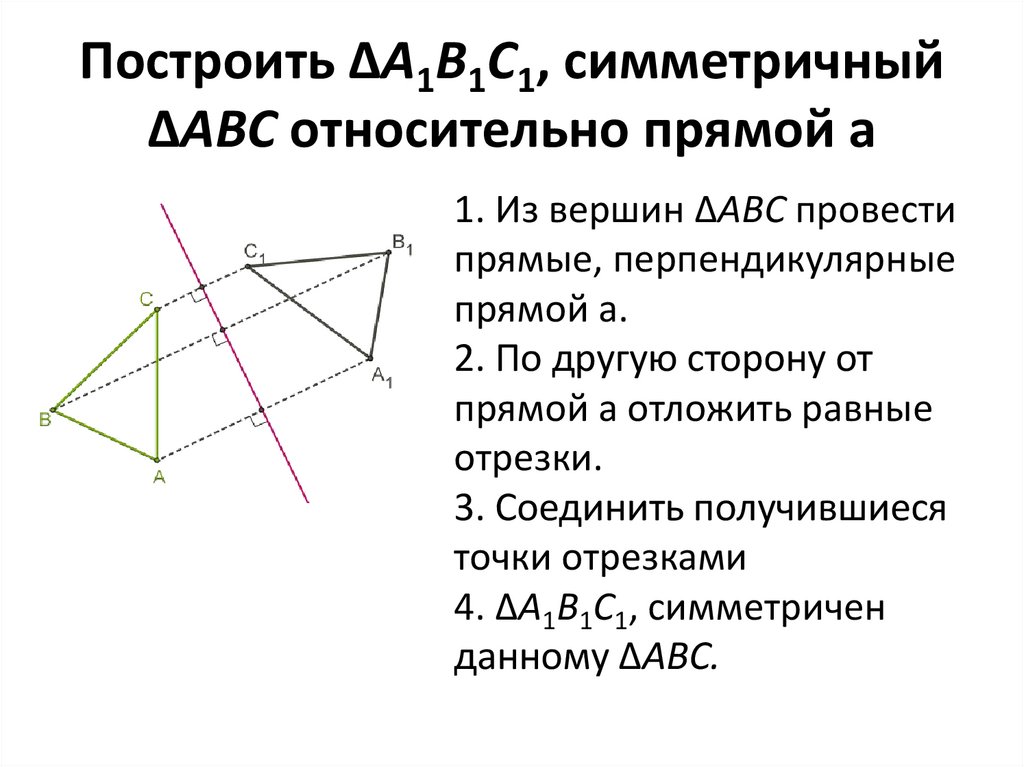
Построить ΔA1B1C1, симметричныйΔABC относительно прямой а
1. Из вершин ΔABC провести
прямые, перпендикулярные
прямой а.
2. По другую сторону от
прямой а отложить равные
отрезки.
3. Соединить получившиеся
точки отрезками
4. ΔA1B1C1, симметричен
данному ΔABC.
9.
Фигуры, симметричные относительнонекоторой прямой, равны
Определение:
Фигура называется симметричной относительно
прямой, если для каждой точки рассматриваемой
фигуры симметричная для неё точка относительно
данной прямой также находится на этой фигуре
10.
Примеры осевой симметрии11.
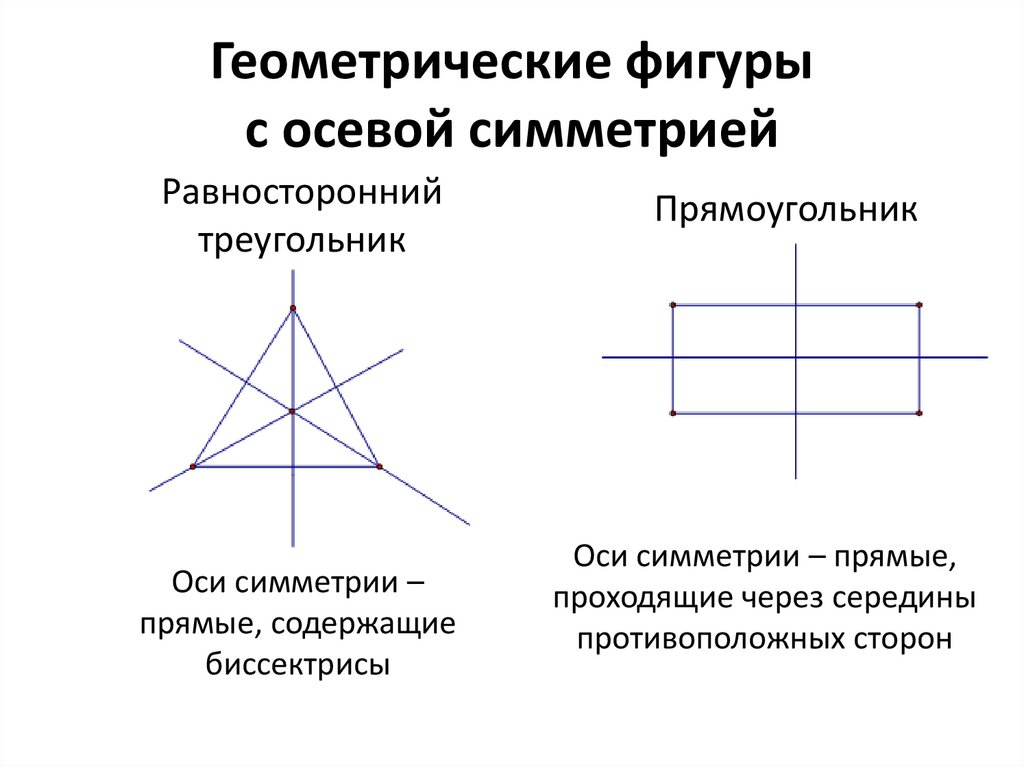
Геометрические фигурыс осевой симметрией
Равносторонний
треугольник
Оси симметрии –
прямые, содержащие
биссектрисы
Прямоугольник
Оси симметрии – прямые,
проходящие через середины
противоположных сторон
12.
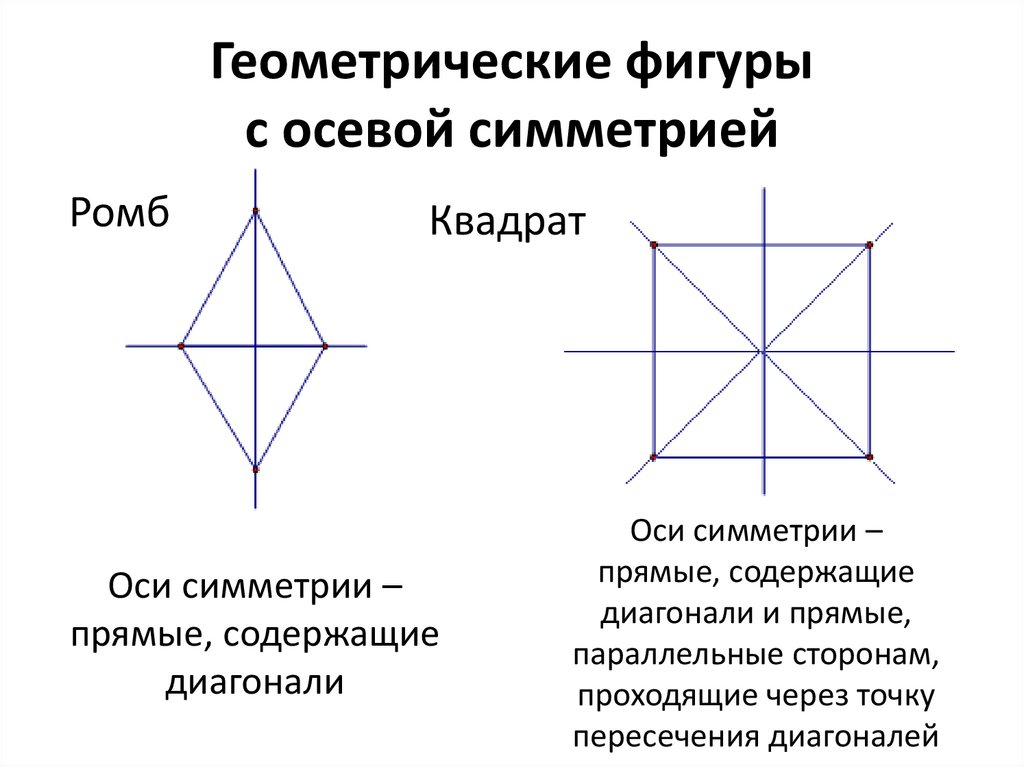
Геометрические фигурыс осевой симметрией
Ромб
Квадрат
Оси симметрии –
прямые, содержащие
диагонали
Оси симметрии –
прямые, содержащие
диагонали и прямые,
параллельные сторонам,
проходящие через точку
пересечения диагоналей



 mathematics
mathematics