Геодезические сети
1. Лекция
ГЕОДЕЗИЧЕСКИЕ СЕТИ2. Геодезическая сеть -
Геодезическая сеть совокупность точек, закрепленныхна земной поверхности, положение
которых определено в общей для
них системе координат и высот.
Различают:
- Плановые сети
(х, у или B,L);
- Высотные сети (Н);
- Пространственные сети
(X, Y, Z или B, L, H)
3.
Методы построения плановых сетейТриангуляция
Трилатерация
Линейно-угловая
Полигонометрия
Спутниковый метод
4.
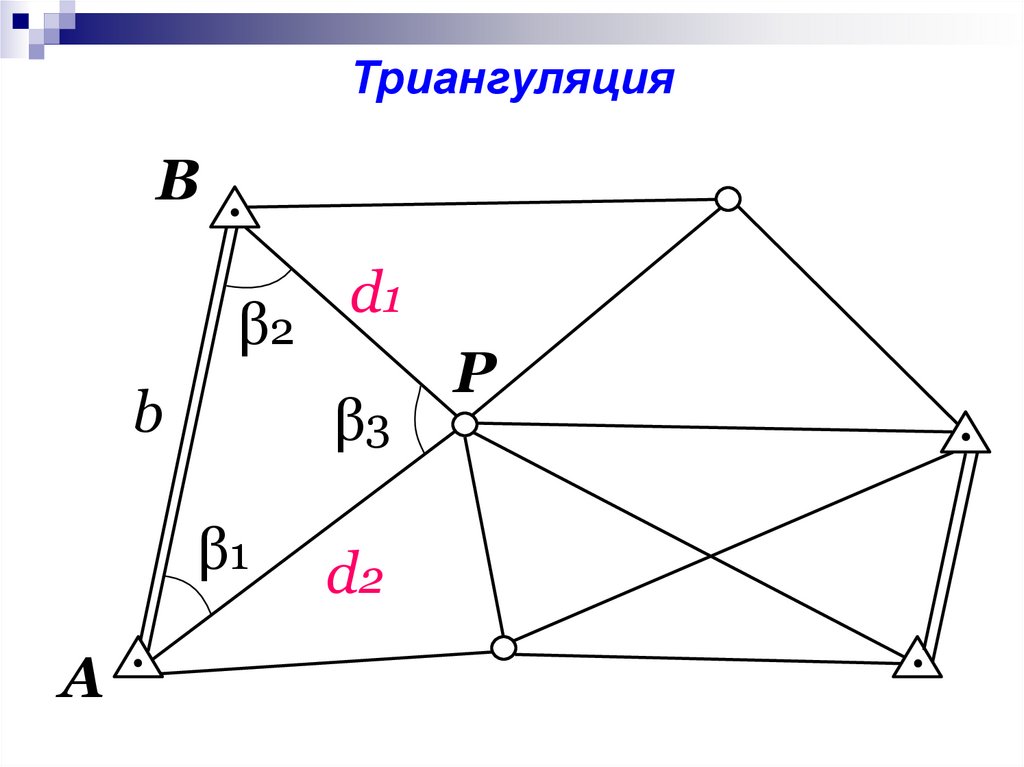
ТриангуляцияB
β2
b
β3
β1
A
d1
d2
P
5.
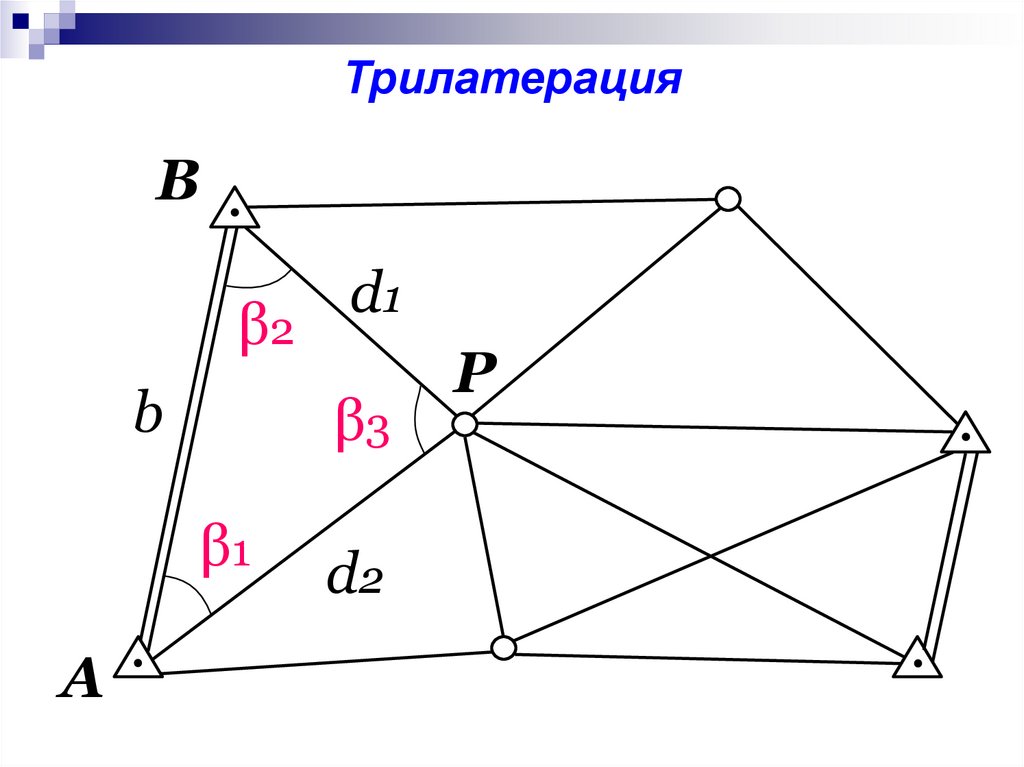
ТрилатерацияB
β2
b
β3
β1
A
d1
d2
P
6.
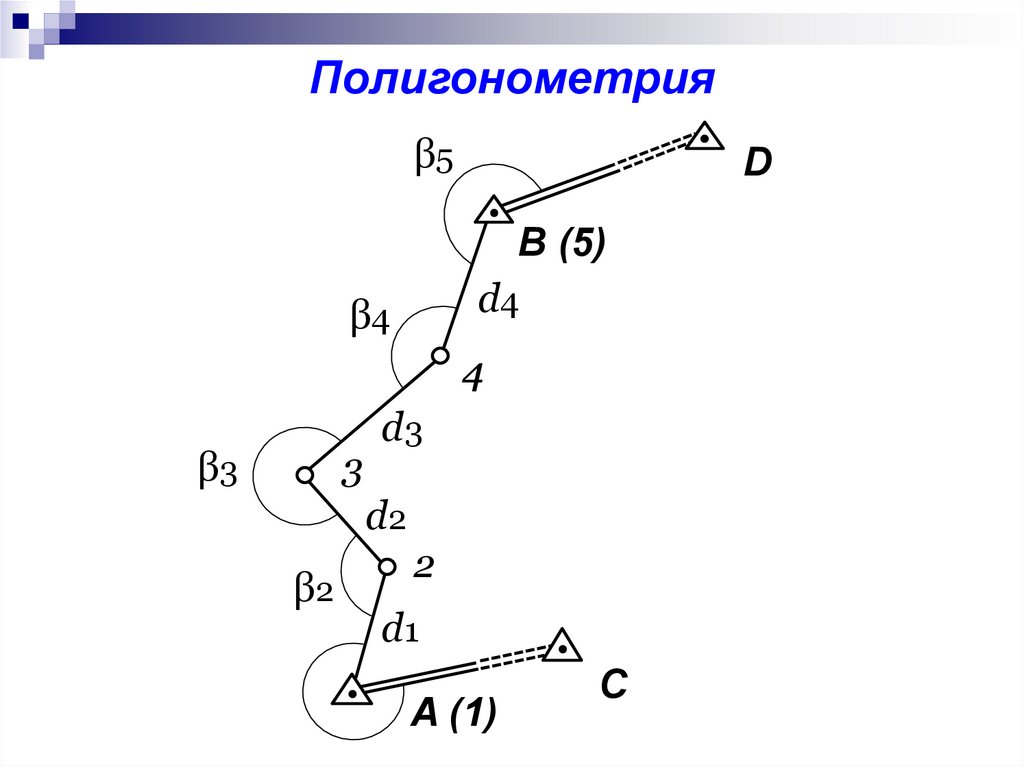
Полигонометрияβ5
D
B (5)
d4
β4
4
β3
3
d3
d2
β2
2
d1
A (1)
С
7.
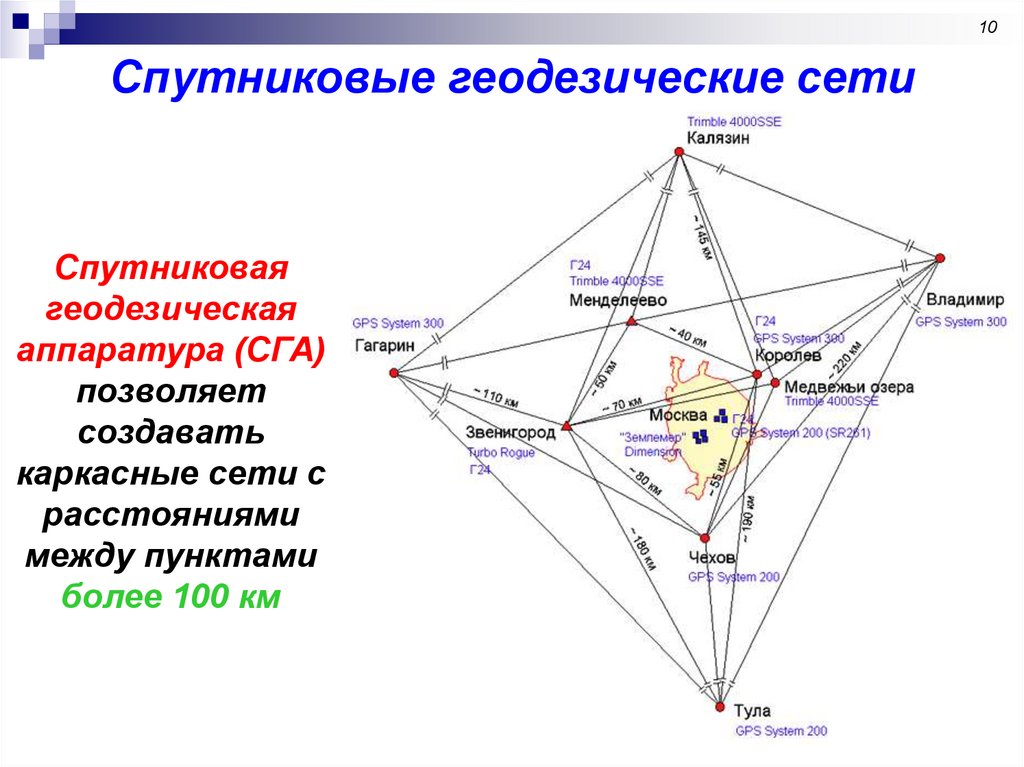
10Спутниковые геодезические сети
Спутниковая
геодезическая
аппаратура (СГА)
позволяет
создавать
каркасные сети с
расстояниями
между пунктами
более 100 км
8.
МЕЖДУНАРОДНАЯ ОСНОВАUnited Nations
Committee of Experts
on Global Geospatial Information Management
IAG Resolutions at the XXVII IUGG General Assembly 2019
Резолюция 1:
Международная
наземная система
отсчета (ITRF)
Рекомендовать
сообществу
пользователей
использовать ITRF в
качестве стандартной
наземной системы
отсчета
Резолюция 3: Создание
Международной системы отсчета
высот (IHRF)
Резолюция 4: Создание
инфраструктуры для
международной системы отсчета
гравитации (IGRS)
Призывает все страны
взаимодействовать с IAG путем:
Установки опорных станций
IHRF на национальном уровне
Проведения гравиметрических
исследований
Описания, архивирования и
предоставления геодезической
для определения
и
QTRS – Казахстанская
наземная связанной
система с IHRF
продукции,
согласования
отсчета
национальных
QHRS и– Казахстанская система отсчета
8региональных систем
высот
отсчета
Призывает международные и
национальные учреждения, агентства и
правительственные органы,
отвечающие за геодезическую
инфраструктуру:
Установить набор опорных станций
абсолютной гравитации на
национальном уровне
Проводить регулярные наблюдения
абсолютной силы тяжести на этих
9.
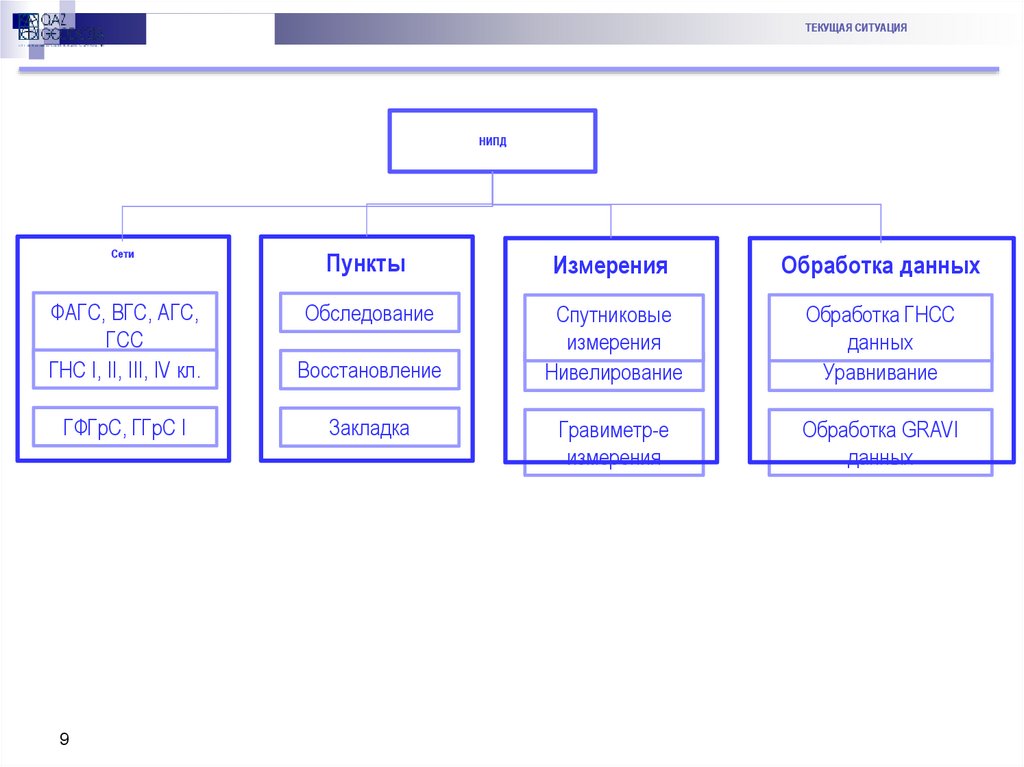
ТЕКУЩАЯ СИТУАЦИЯНИПД
Сети
Пункты
Измерения
Обработка данных
ФАГС, ВГС, АГС,
ГСС
ГНС I, II, III, IV кл.
Обследование
Восстановление
Спутниковые
измерения
Нивелирование
Обработка ГНСС
данных
Уравнивание
ГФГрС, ГГрС I
Закладка
Гравиметр-е
измерения
Обработка GRAVI
данных
9
10.
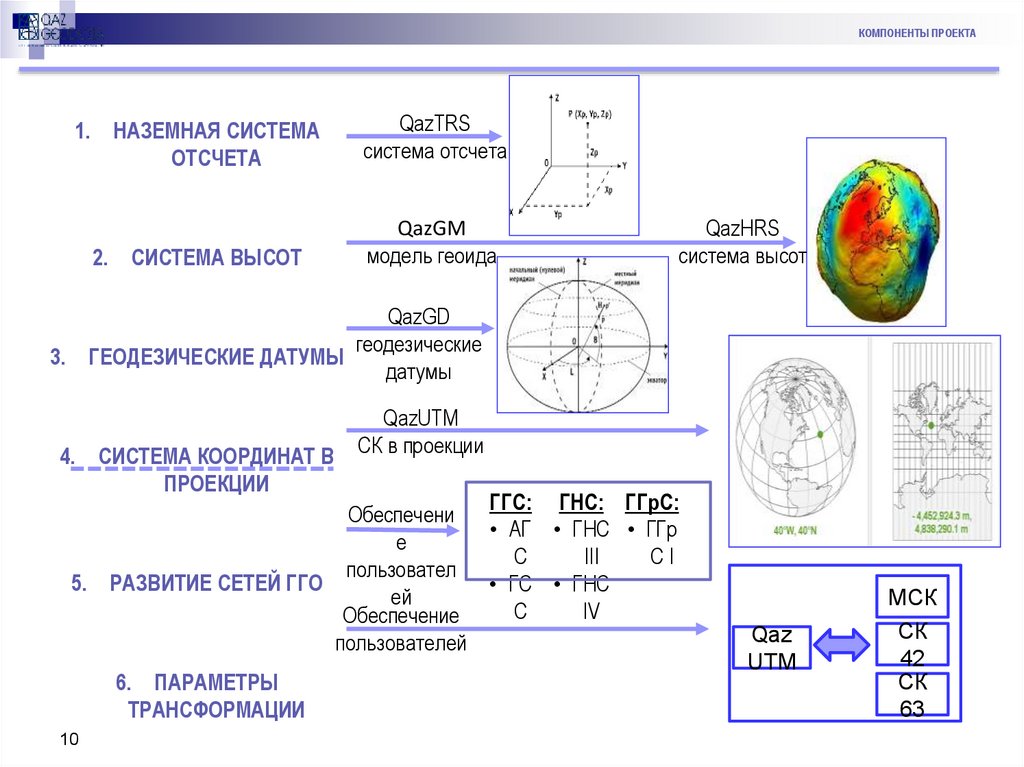
КОМПОНЕНТЫ ПРОЕКТА1.
2.
НАЗЕМНАЯ СИСТЕМА
ОТСЧЕТА
QazTRS
cистема отсчета
СИСТЕМА ВЫСОТ
QazGM
модель геоида
QazHRS
система высот
QazGD
геодезические
ГЕОДЕЗИЧЕСКИЕ ДАТУМЫ
датумы
3.
4.
5.
СИСТЕМА КООРДИНАТ В
ПРОЕКЦИИ
ГГС: ГНС: ГГрС:
Обеспечени
• АГ • ГНС • ГГр
е
С
III
СI
пользовател
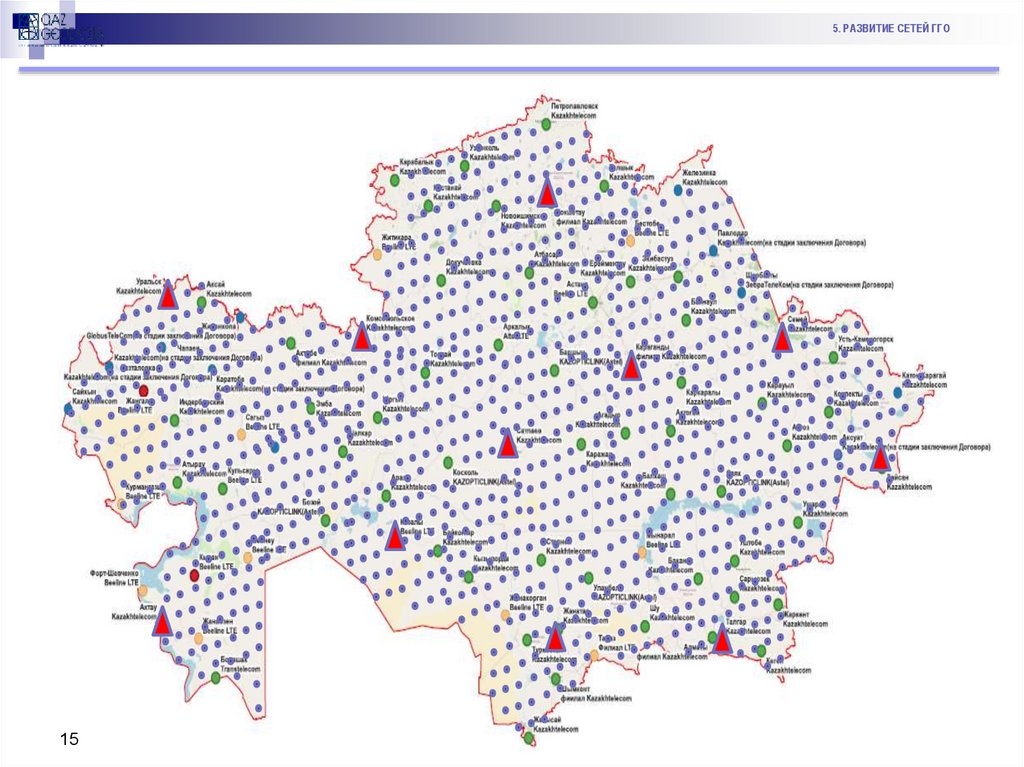
РАЗВИТИЕ СЕТЕЙ ГГО
• ГС • ГНС
ей
С
IV
Обеспечение
пользователей
6. ПАРАМЕТРЫ
ТРАНСФОРМАЦИИ
10
QazUTM
СК в проекции
Qaz
UTM
МСК
СК
42
СК
63
11.
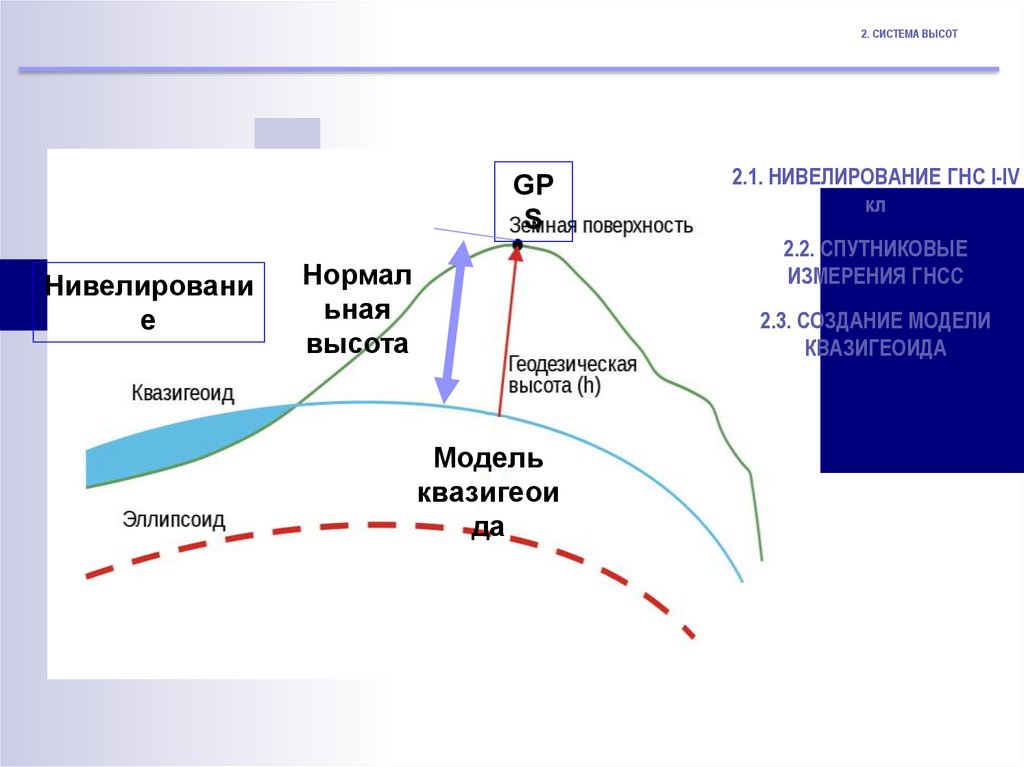
2. СИСТЕМА ВЫСОТGP
S
Нивелировани
е
2.1. НИВЕЛИРОВАНИЕ ГНС I-IV
кл
2.2. СПУТНИКОВЫЕ
ИЗМЕРЕНИЯ ГНСС
Нормал
ьная
высота
2.3. СОЗДАНИЕ МОДЕЛИ
КВАЗИГЕОИДА
Модель
квазигеои
да
12.
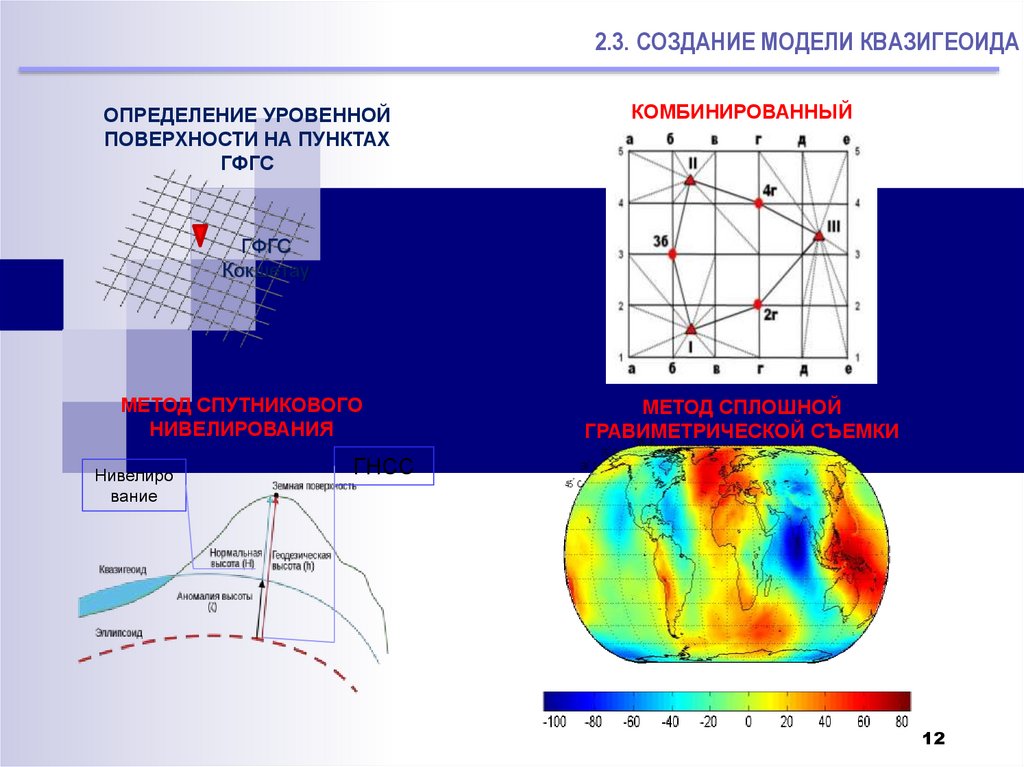
2.3. СОЗДАНИЕ МОДЕЛИ КВАЗИГЕОИДАОПРЕДЕЛЕНИЕ УРОВЕННОЙ
ПОВЕРХНОСТИ НА ПУНКТАХ
ГФГС
КОМБИНИРОВАННЫЙ
КАРКАСНЫЙ МЕТОД
ГФГС
Кокшетау
МЕТОД СПУТНИКОВОГО
НИВЕЛИРОВАНИЯ
Нивелиро
вание
МЕТОД СПЛОШНОЙ
ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ
ГНСС
12
13.
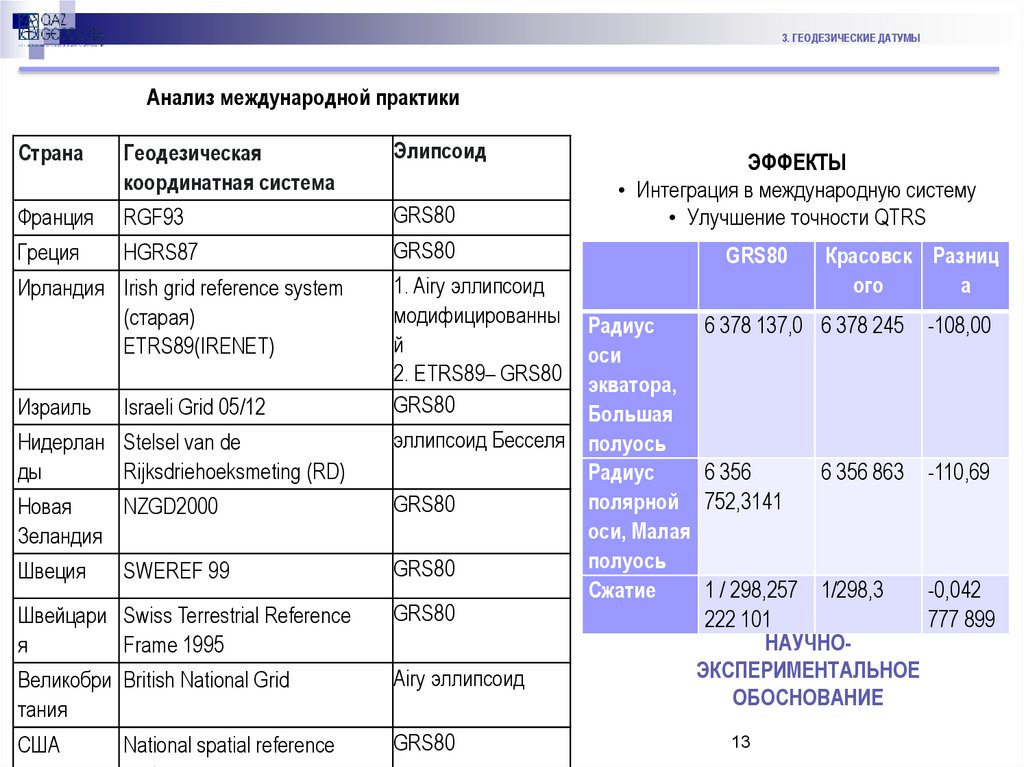
3. ГЕОДЕЗИЧЕСКИЕ ДАТУМЫАнализ международной практики
Страна
Геодезическая
координатная система
Элипсоид
Франция
RGF93
GRS80
Греция
HGRS87
GRS80
Ирландия Irish grid reference system
(старая)
ETRS89(IRENET)
Израиль
Israeli Grid 05/12
Нидерлан Stelsel van de
ды
Rijksdriehoeksmeting (RD)
Новая
NZGD2000
Зеландия
Швеция
SWEREF 99
Швейцари Swiss Terrestrial Reference
я
Frame 1995
Великобри British National Grid
тания
США
National spatial reference
ЭФФЕКТЫ
• Интеграция в международную систему
• Улучшение точности QTRS
GRS80
1. Airy эллипсоид
модифицированны
й
2. ETRS89– GRS80
GRS80
Красовск Разниц
ого
а
Радиус
6 378 137,0 6 378 245 -108,00
оси
экватора,
Большая
эллипсоид Бесселя полуось
Радиус
6 356
6 356 863 -110,69
полярной 752,3141
GRS80
оси, Малая
полуось
GRS80
Сжатие
1 / 298,257 1/298,3
-0,042
GRS80
222 101
777 899
НАУЧНОЭКСПЕРИМЕНТАЛЬНОЕ
Airy эллипсоид
ОБОСНОВАНИЕ
GRS80
13
14.
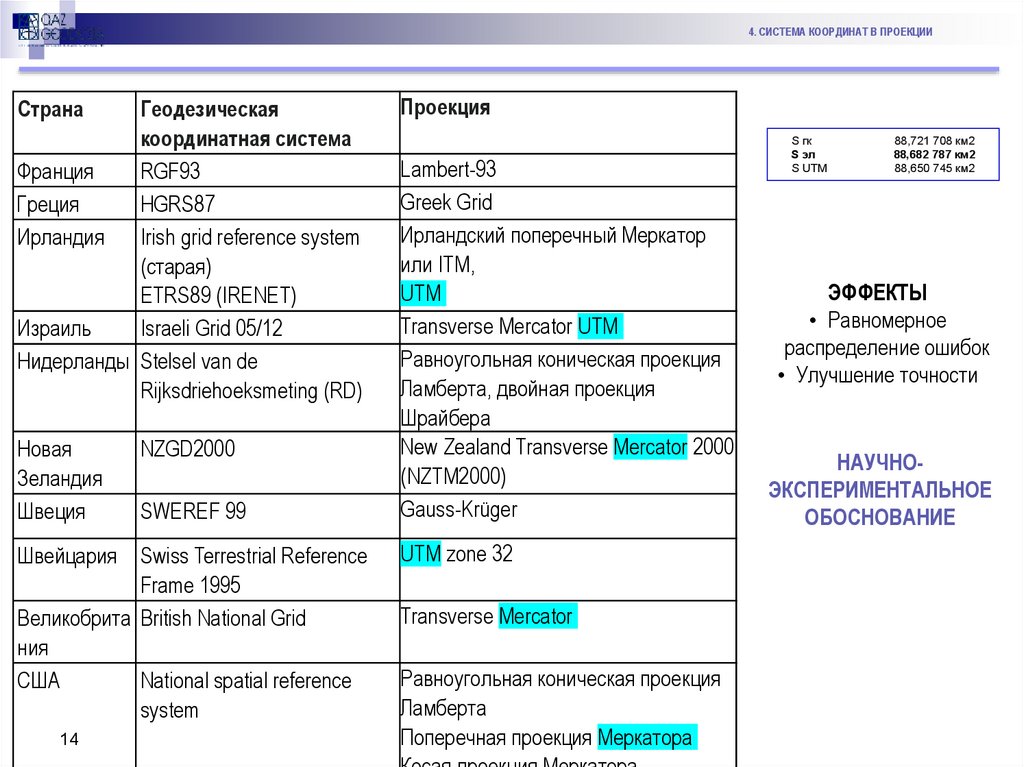
4. СИСТЕМА КООРДИНАТ В ПРОЕКЦИИСтрана
Геодезическая
координатная система
Франция
RGF93
Греция
HGRS87
Ирландия
Irish grid reference system
(старая)
ETRS89 (IRENET)
Израиль
Israeli Grid 05/12
Нидерланды Stelsel van de
Rijksdriehoeksmeting (RD)
Новая
Зеландия
Швеция
Швейцария
NZGD2000
SWEREF 99
Swiss Terrestrial Reference
Frame 1995
Великобрита British National Grid
ния
США
National spatial reference
system
14
Проекция
Lambert-93
Greek Grid
Ирландский поперечный Меркатор
или ITM,
UTM
Transverse Mercator UTM
Равноугольная коническая проекция
Ламберта, двойная проекция
Шрайбера
New Zealand Transverse Mercator 2000
(NZTM2000)
Gauss-Krüger
UTM zone 32
Transverse Mercator
Равноугольная коническая проекция
Ламберта
Поперечная проекция Меркатора
S гк
S эл
S UTM
88,721 708 км2
88,682 787 км2
88,650 745 км2
ЭФФЕКТЫ
• Равномерное
распределение ошибок
• Улучшение точности
НАУЧНОЭКСПЕРИМЕНТАЛЬНОЕ
ОБОСНОВАНИЕ
15.
5. РАЗВИТИЕ СЕТЕЙ ГГО15
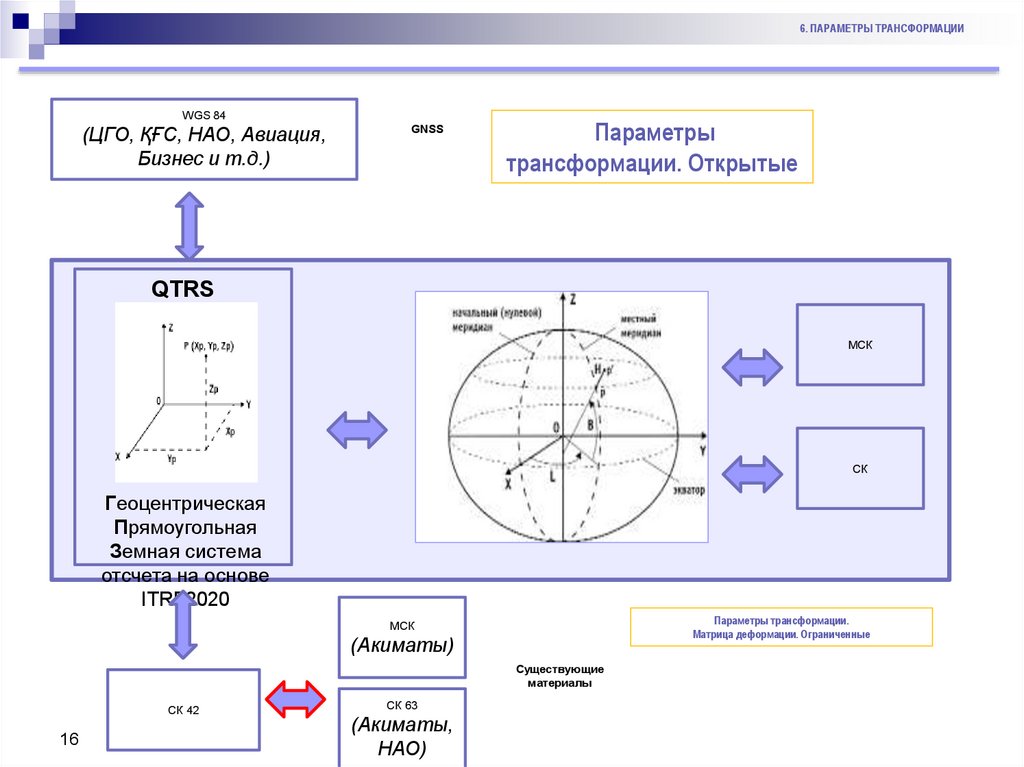
16.
6. ПАРАМЕТРЫ ТРАНСФОРМАЦИИWGS 84
(ЦГО, ҚҒС, НАО, Авиация,
Бизнес и т.д.)
GNSS
Параметры
трансформации. Открытые
QTRS
МСК
СК
Геоцентрическая
Прямоугольная
Земная система
отсчета на основе
ITRF2020
Параметры трансформации.
Матрица деформации. Ограниченные
МСК
(Акиматы)
Существующие
материалы
СК 42
16
СК 63
(Акиматы,
НАО)
17.
6. ПАРАМЕТРЫ ТРАНСФОРМАЦИИМатрица деформации МСК Отраслевые ГО / КГК
QTRS
ПАРАМЕТРЫ
ТРАНСФОРМАЦИИ
МСК
17
СК-42
МАТРИЦ
А
ДЕФОРМ
АЦИИ
18.
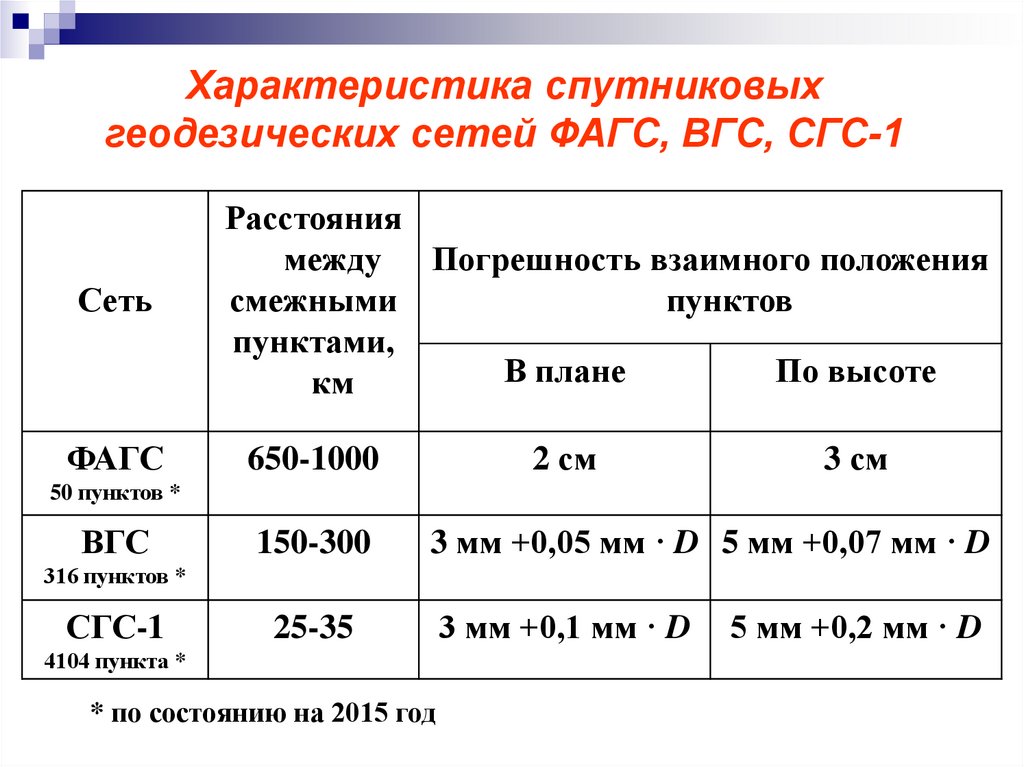
Характеристика спутниковыхгеодезических сетей ФАГС, ВГС, СГС-1
Сеть
Расстояния
между Погрешность взаимного положения
смежными
пунктов
пунктами,
В плане
По высоте
км
ФАГС
650-1000
2 см
3 см
50 пунктов *
ВГС
150-300
3 мм +0,05 мм · D 5 мм +0,07 мм · D
25-35
3 мм +0,1 мм · D
316 пунктов *
СГС-1
4104 пункта *
* по состоянию на 2015 год
5 мм +0,2 мм · D
19. ЗАКРЕПЛЕНИЕ ПУНКТОВ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ
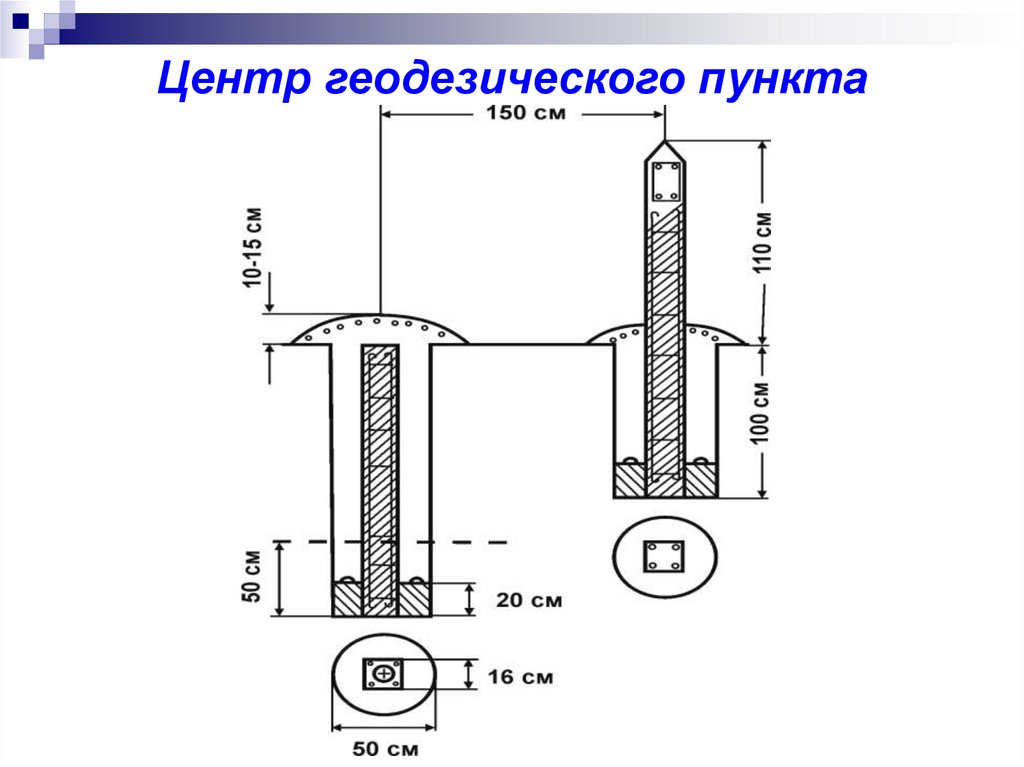
20.
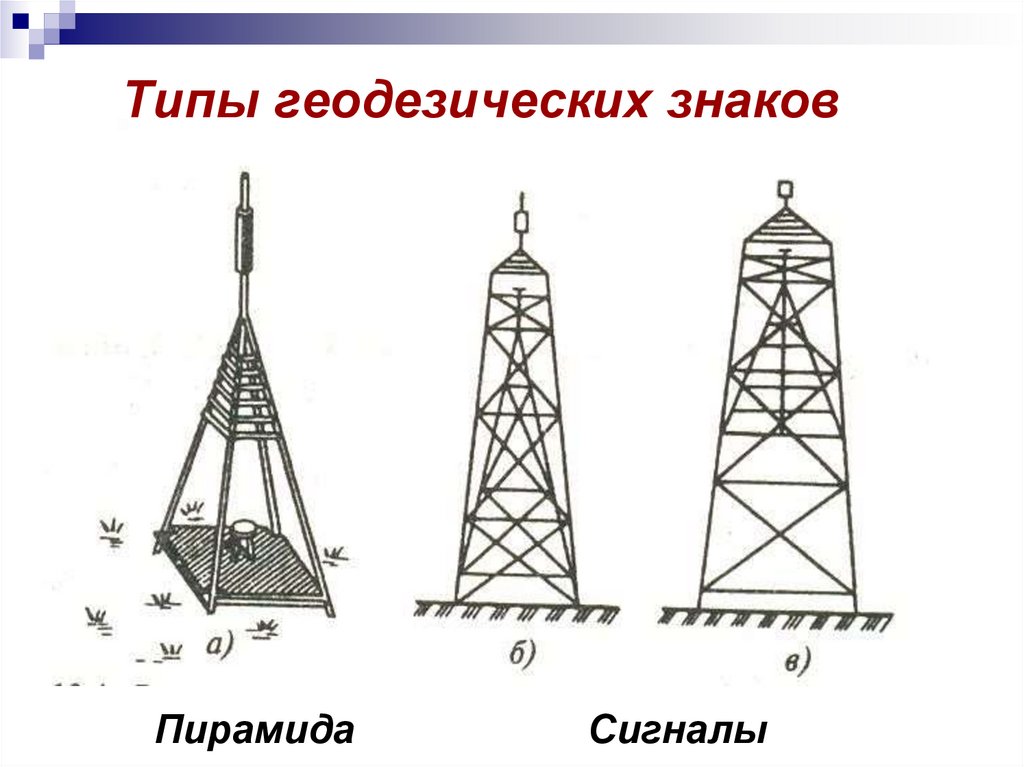
Центр геодезического пункта21. Типы геодезических знаков
ПирамидаСигналы
22. Пункт геодезической разбивочной сети на строительстве КАД
23. Пункт съёмочной сети
24. ТЕОДОЛИТНЫЙ ХОД
25. ТЕОДОЛИТНЫЙ ХОД
-ход полигонометрии пониженной
точности.
Применяется, в основном, для
создания съемочных сетей.
26.
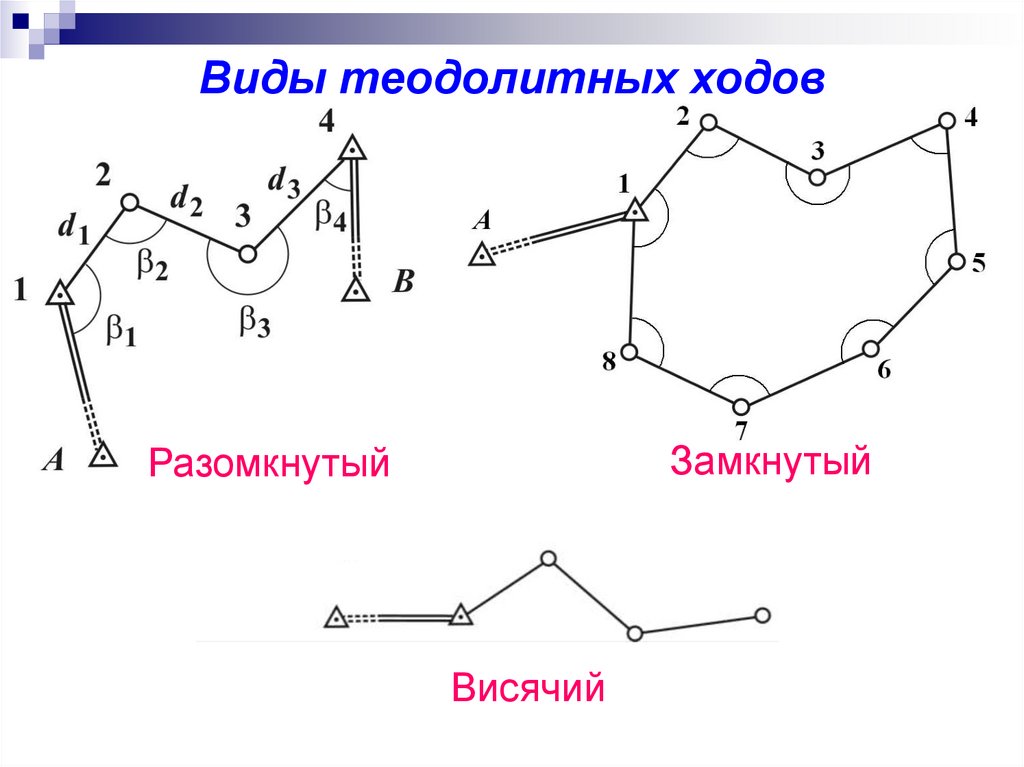
Виды теодолитных ходовЗамкнутый
Разомкнутый
Висячий
27. Последовательность работ при прокладке теодолитного хода
1.2.
3.
4.
Проектирование хода на
топографической карте или плане.
Рекогносцировка и закрепление точек
хода на местности.
Измерение углов поворота и длин
сторон в ходе.
Обработка теодолитного хода
(вычисления в ведомости координат).
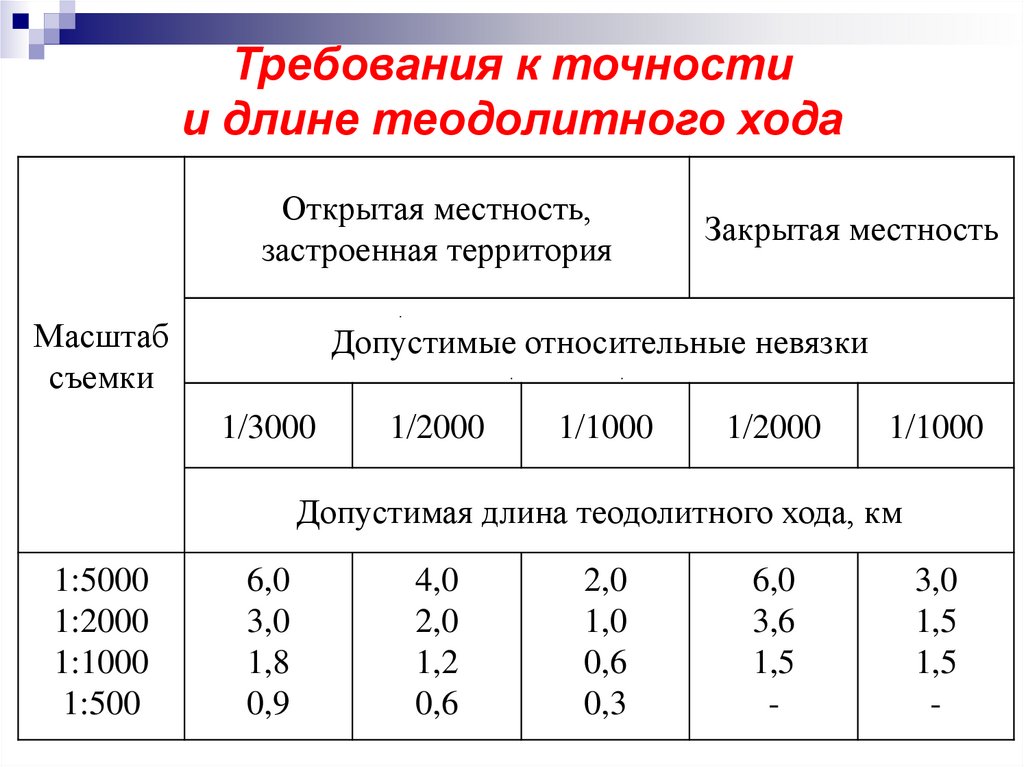
28.
Требования к точностии длине теодолитного хода
Открытая местность,
застроенная территория
Масштаб
съемки
Закрытая местность
Допустимые относительные невязки
1 3000
1 2000
1 1000
1 2000
1 1000
Допустимая длина теодолитного хода, км
1:5000
1:2000
1:1000
1:500
6,0
3,0
1,8
0,9
4,0
2,0
1,2
0,6
2,0
1,0
0,6
0,3
6,0
3,6
1,5
-
3,0
1,5
1,5
-
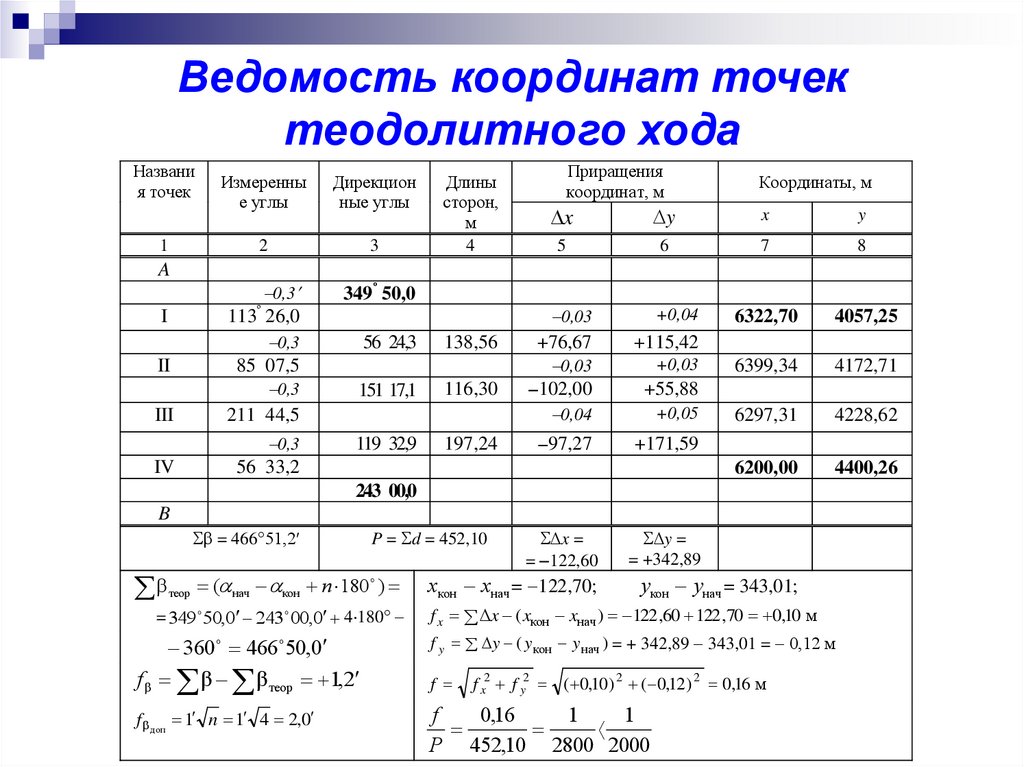
29.
Ведомость координат точектеодолитного хода
Названи
я точек
1
Измеренны
е углы
Дирекцион
ные углы
2
3
A
0,3
I
II
III
113º 26,0
0,3
85 07,5
0,3
211 44,5
0,3
IV
Длины
сторон,
м
4
349º 50,0
56 24,3
151 17,1
119 32,9
138,56
116,30
197,24
Приращения
координат, м
Координаты, м
x
y
x
y
5
6
7
8
0,03
+0,04
6322,70
4057,25
+76,67
0,03
102,00
0,04
+115,42
6399,34
4172,71
6297,31
4228,62
97,27
+171,59
6200,00
4400,26
+0,03
+55,88
+0,05
56 33,2
243 00,0
B
= 466 51,2′
β
теор
P = d = 452,10
( нач кон n 180 )
x =
= 122,60
xкон xнач = 122,70;
y =
= +342,89
yкон yнач = 343,01;
= 349 50,0 243 00,0 4 180
f x x ( xкон xнач ) 122 ,60 122 ,70 0,10 м
360 466 50,0
f y y ( y кон y нач ) = + 342,89 343,01 = 0,12 м
f β β β теор 1,2
f доп 1 n 1 4 2,0
f
f x2 f y2 ( 0,10 ) 2 ( 0,12 ) 2 0,16 м
f
0,16
1
1
P 452,10 2800 2000
30. Обработка замкнутого теодолитного хода
Угловая невязка:f изм. 180 (n 2)
f д о п. 1
Линейные невязки:
f x xi
f y yi
f абс.
f x2 f y2
f отн.
f абс.
1
P
2000
n
31. ЗАСЕЧКИ
32.
aб
Р
Р
в
D
С
β3
β1
β2
Р
β1
А
β2
С
B
А
B
Р
г
д
d1
А
С
B
Р
d3
d2
А
B
С
А
B
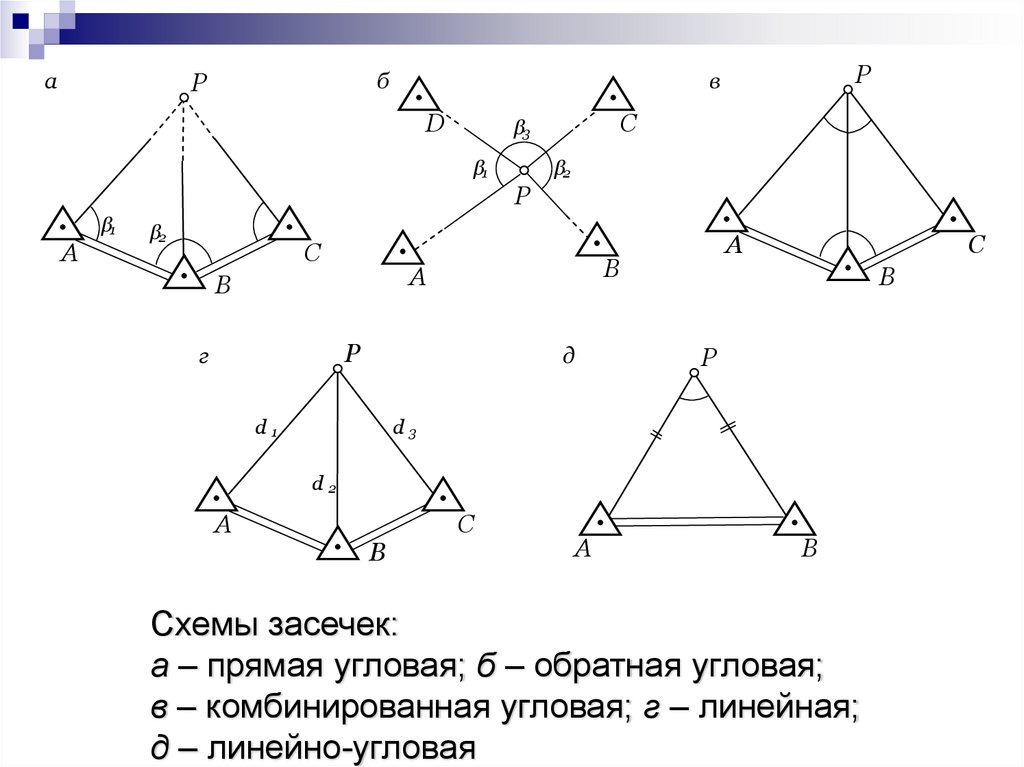
Схемы засечек:
а – прямая угловая; б – обратная угловая;
в – комбинированная угловая; г – линейная;
д – линейно-угловая
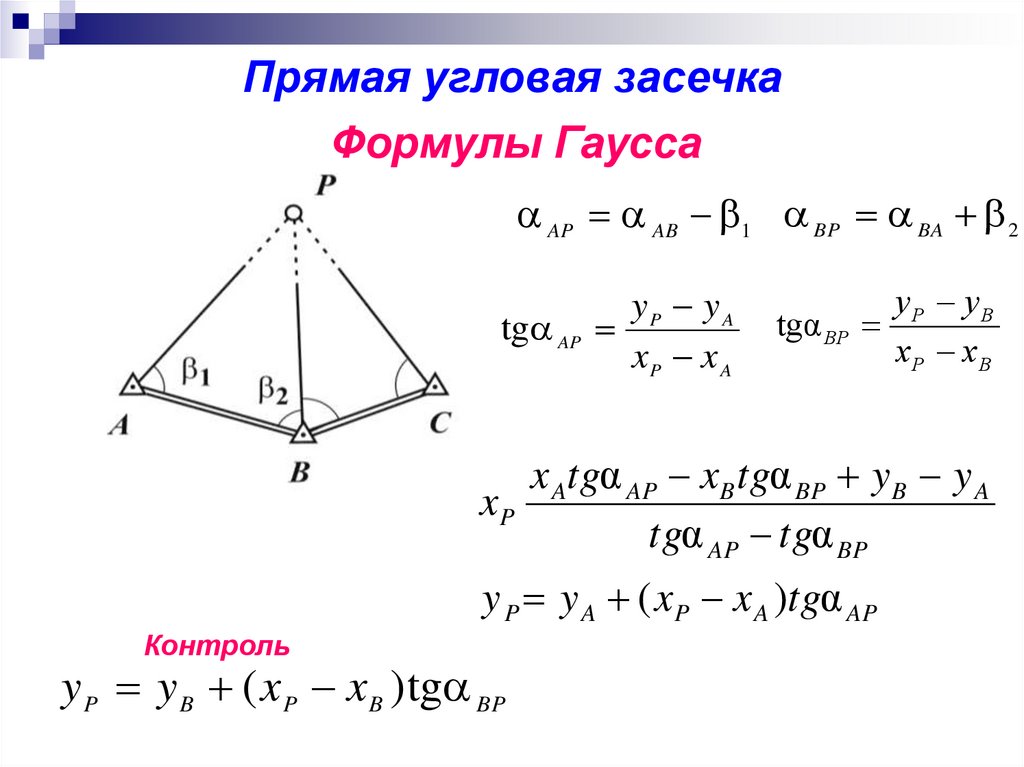
33.
Прямая угловая засечкаФормулы Гаусса
AP AB 1 BP BA 2
yP y A
tg AP
xP x A
yP yB
tgα BP
xP xB
x Atgα AP xB tgα BP y B y A
xP
tgα AP tgα BP
y P y A ( xP x A )tgα AP
Контроль
y P y B ( x P x B ) tg BP
34.
Прямая угловая засечкаФормулы Юнга
x Actg 2 xB ctg 1 y B y A
xP
ctg 1 ctg 2
y Actg 2 y B ctg 1 x A xB
yP
ctg 1 ctg 2
35.
Обратная угловая засечкаy Actgβ1 yB (ctgβ1 ctgβ 2 ) yC ctgβ 2 xA xC
tgα BP
xActgβ1 xB (ctgβ1 ctgβ 2 ) xC ctgβ 2 y A yC
AP BP 1















 geography
geography