Кеңістіктегі векторлар және оларға амалдар қолдану

1. Сабақтың тақырыбы: Кеңістіктегі векторлар және оларға амалдар қолдану

2.

Оқыту мақсаты
10.4.1 - кеңістіктегі вектор, вектордың ұзындығы, тең
векторлар анықтамаларын білу,
10.4.2 - векторларды қосу және векторды санға көбейтуді
орындау;

3.

Бағалау критерийлері
Вектор түсінігін біледі және кеңістікте векторларға
сызықты амалдарды қолдана алады
Векторларды қосу, алу тәсілдерін біледі
Векторды санға дұрыс көбейтеді

4. ФИЗИКА

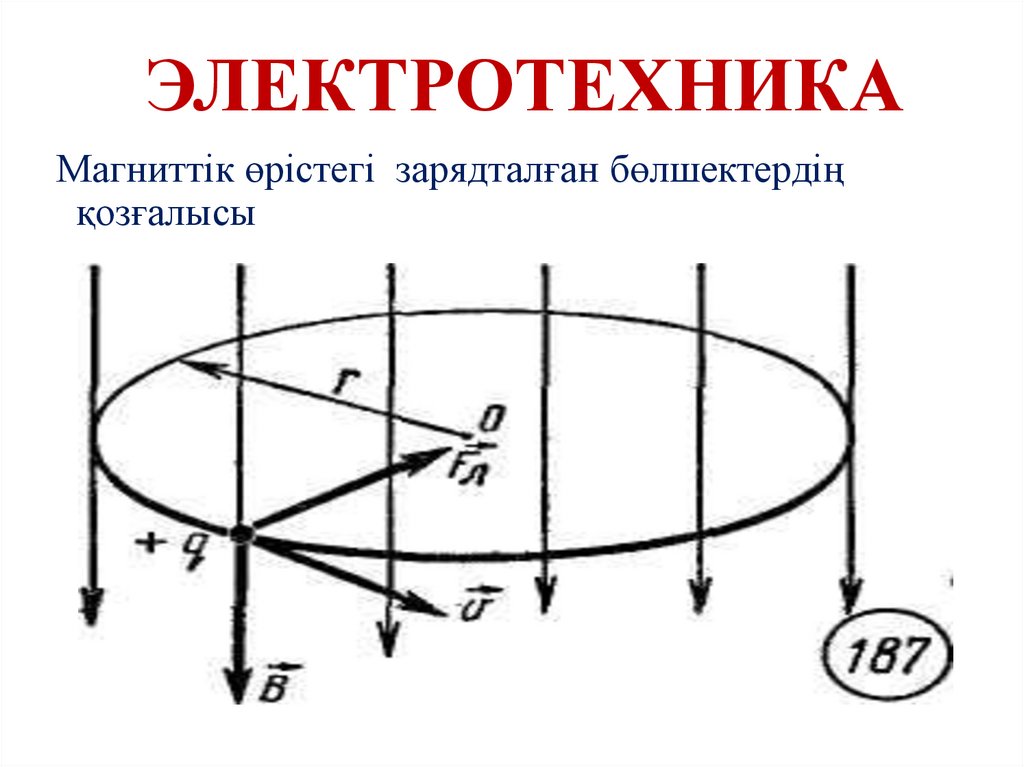
Дененің қозғалу бағыты

5. ЭЛЕКТРОТЕХНИКА

Магниттік өрістегі зарядталған бөлшектердің
қозғалысы

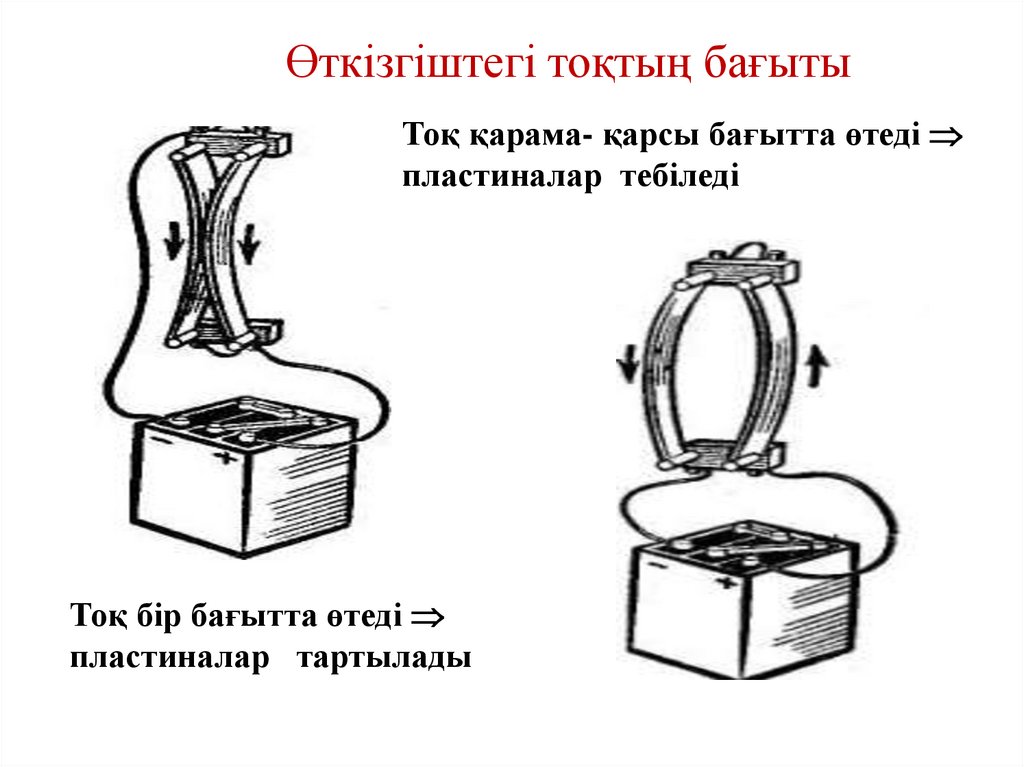
6. Өткізгіштегі тоқтың бағыты

Тоқ қарама- қарсы бағытта өтеді
пластиналар тебіледі
Тоқ бір бағытта өтеді
пластиналар тартылады

7. Ұштарының қайсысы басы және қайсысы ұшы екені көрсетілген бағытталған кесінді вектор деп аталады.

Кеңістіктегі векторлар ұғымы
Ұштарының қайсысы басы және қайсысы ұшы екені
көрсетілген бағытталған кесінді вектор деп аталады.
Кеңістіктің кез келген нүктесін вектор деп қарастыруға болады.
Мұндай векторлар нөлдік векторлар деп аталады.
Нөлдік векторлардың басы мен ұшы беттеседі, сондықтан ол
векторлардың қандай да бір айқын бағыты болмайды.
а) AB және CD - нөлдік емес векторлар,
ТТ - нөлдік вектор, ТТ 0
б) a , b және с
нөлдік емес векторлар

8. АВ кесіндінің ұзындығы нөлдік емес векторының ұзындығы деп аталады.

Вектор ұзындығы
АВ кесіндінің ұзындығы AB нөлдік
AB AB, а AB
емес векторының ұзындығы деп аталады.
Нөлдік вектордың ұзындығы
нөлге тең деп саналады.
0 0

9. Бағыттас векторлар

Егер векторлар бас нүктелері арқылы өтетін түзудің бір
жағында жатса, бағыттас векторлар деп аталады.
a
a b
b
Нөлдік векторды кез келген вектормен бағыттас деп есептеу
келісілген.

10. Қарама-қарсы бағытталған вектор

Егер векторлар бас нүктелері арқылы өтетін түзудің әр жағында
жатса, қарама-қарсы бағытталған векторлар деп аталады.
a
b
a b

11. Тең векторлар

Тең векторлар -ұзындықтары бірдей бағыттас
векторлар.
a
a b a b, a b
b
Кез келген нүктеден берілген векторға тең вектор
өлшеп салуға болады және ол тек біреу ғана.

12. Қарама-қарсы векторлар

Қарама-қарсы векторлар– бағыттары қарама-қарсы,
ұзындықтары тең векторлар.
a
b
a b a b, a b
Нөлдік векторға қарсы вектор нөлдік вектор деп аталады

13. Векторларды қосу

Үшбұрыш ережесі
Параллелограмм ережесі
Көпбұрыш ережесі
Параллелепипед ережесі
Қосу қасиеттері

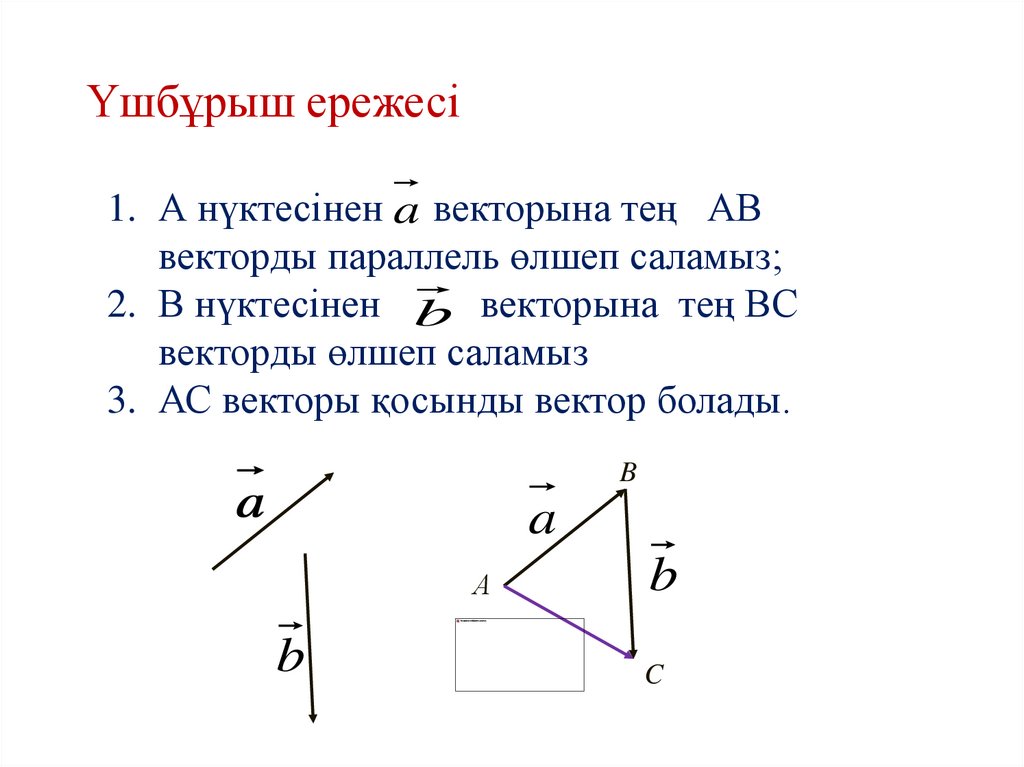
14. Үшбұрыш ережесі

1. А нүктесінен a векторына тең АВ
векторды параллель өлшеп саламыз;
2. В нүктесінен b векторына тең ВС
векторды өлшеп саламыз
3. АС векторы қосынды вектор болады.
B
a
a
А
b
b
C

15. Үшбұрыш ережесі

B
a
А
b
a b
C
Кез келген А, В және С нүктелері үшін
мына теңдік орындалады: AB BC AC

16. Параллелограмм ережесі

1 . А нүктесінен a векторына тең АВ векторын b
және векторына тең АС векторын өлшеп салып,
параллелограмға дейін сызықтармен
толықтырамыз;
2. Шыққан параллелограмның диагоналы қосынды
вектор болады.
B
a
a
b
b C
А
с
a
b

17. Қосу қасиеттері

Кез келген a, b және с векторлары үшін мына
теңдіктер орындалады:
a+b= b+a ауыстырымдылық
(a+b)+c= a+(b+c) терімділік

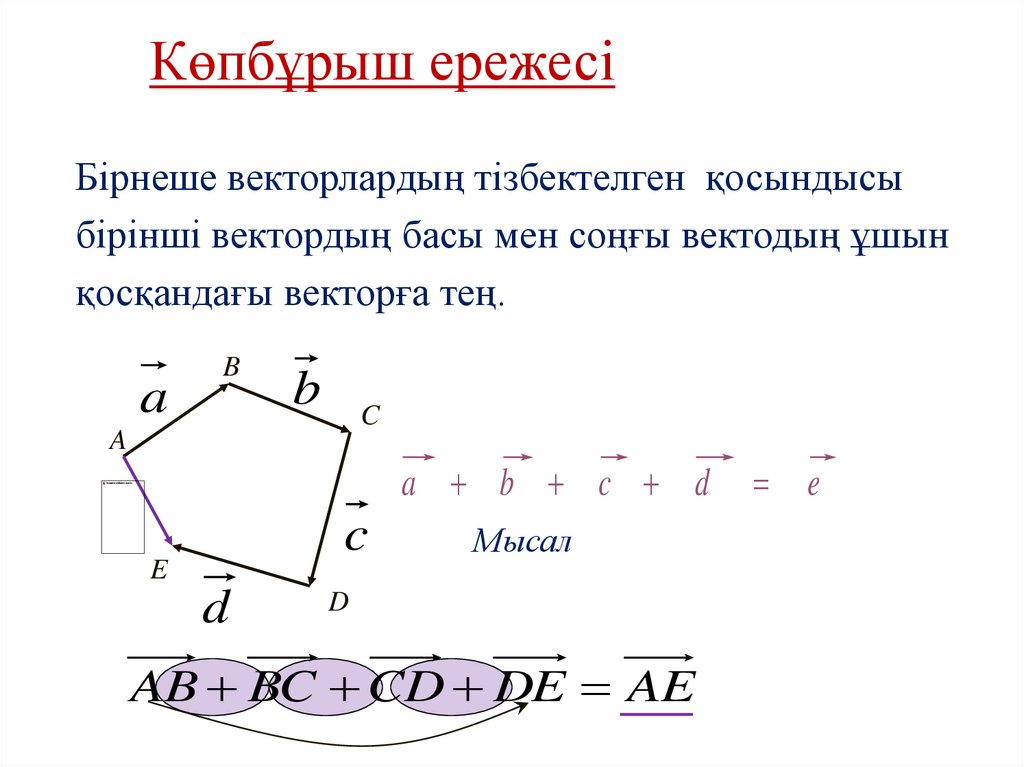
18. Көпбұрыш ережесі

Бірнеше векторлардың тізбектелген қосындысы
бірінші вектордың басы мен соңғы вектодың ұшын
қосқандағы векторға тең.
a
B
b
C
A
a b c d
c
E
d
Мысал
D
AB BC CD DE AE
e

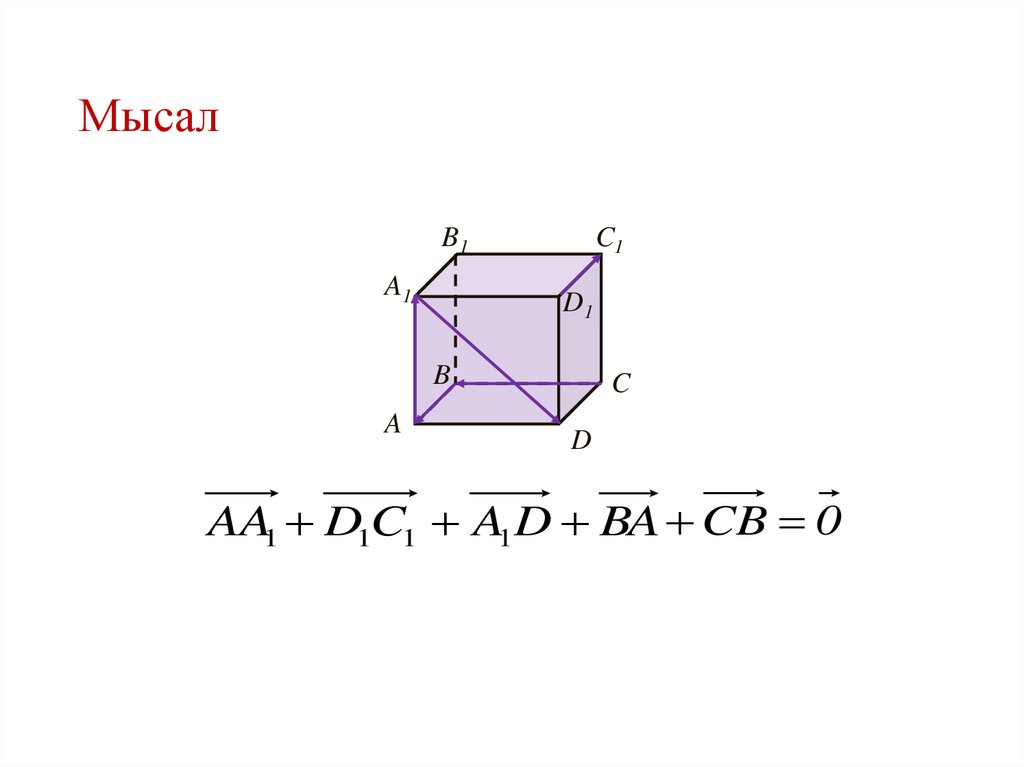
19. Мысал

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

20. Параллелепипед ережесі

Параллелепипедтің диагоналы бойында жататын
вектор осы нүктеден шығатын параллелепипедтің
үш өлшемі бойында жатқан векторлардың
қосындысына тең.
B
C1
A1 1
А
AB b
D1
B
AD a
C
D
AC1 AD AB AA1
AA1 c
AC1 d

21. Қасиеті

B1
C1
A1
D1
B
C
А
D
d
2
d = a+ b+ с – кез келген параллелепипед үшін
2
2
2
2
d = а в с - Тік параллелепипед үшін

22. Векторларды азайту

Азайту.
Қарама-қарсы векторды қосу

23. Азайту

Бір вектордан екінші векторды азайту үшін:
1. Қандай да бір А нүктесінен a векторына тең АВ
векторын өлшеп саламыз ;
2. Осы А нүктесінен АС векторын өлшеп саламыз;
3. a және bвекторларының айырымы ВС векторы
болады.
B
a
b
Үш нүкте ережесі
a
A
a b
b
C

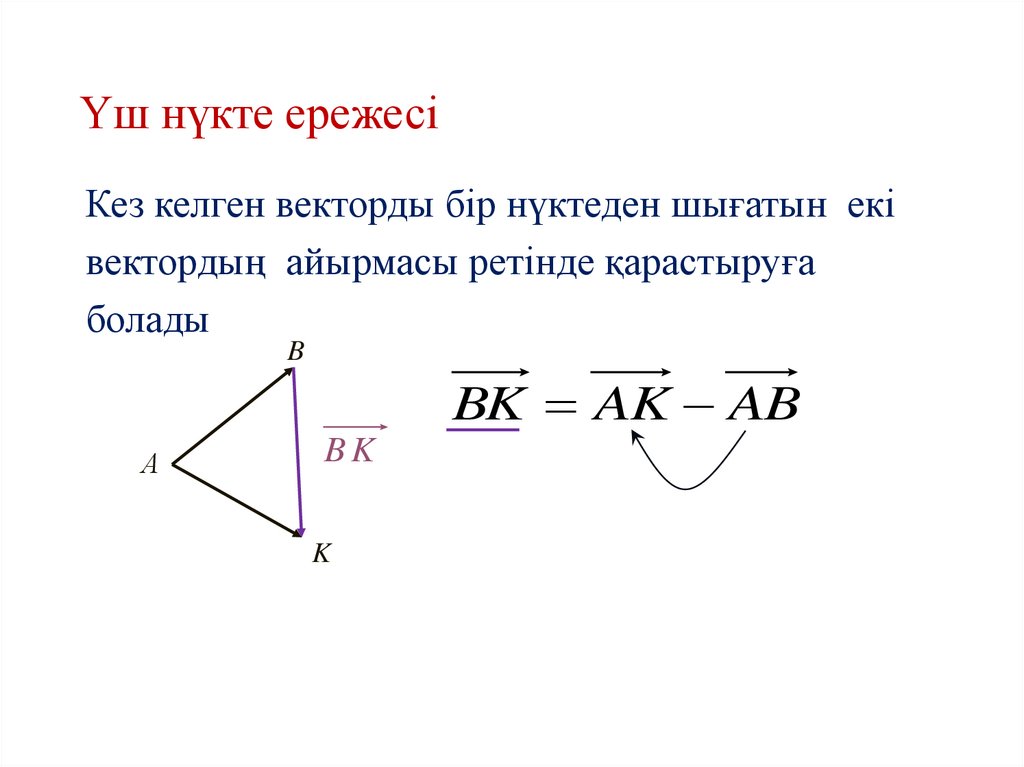
24. Үш нүкте ережесі

Кез келген векторды бір нүктеден шығатын екі
вектордың айырмасы ретінде қарастыруға
болады
B
BK AK AB
А
BK
K

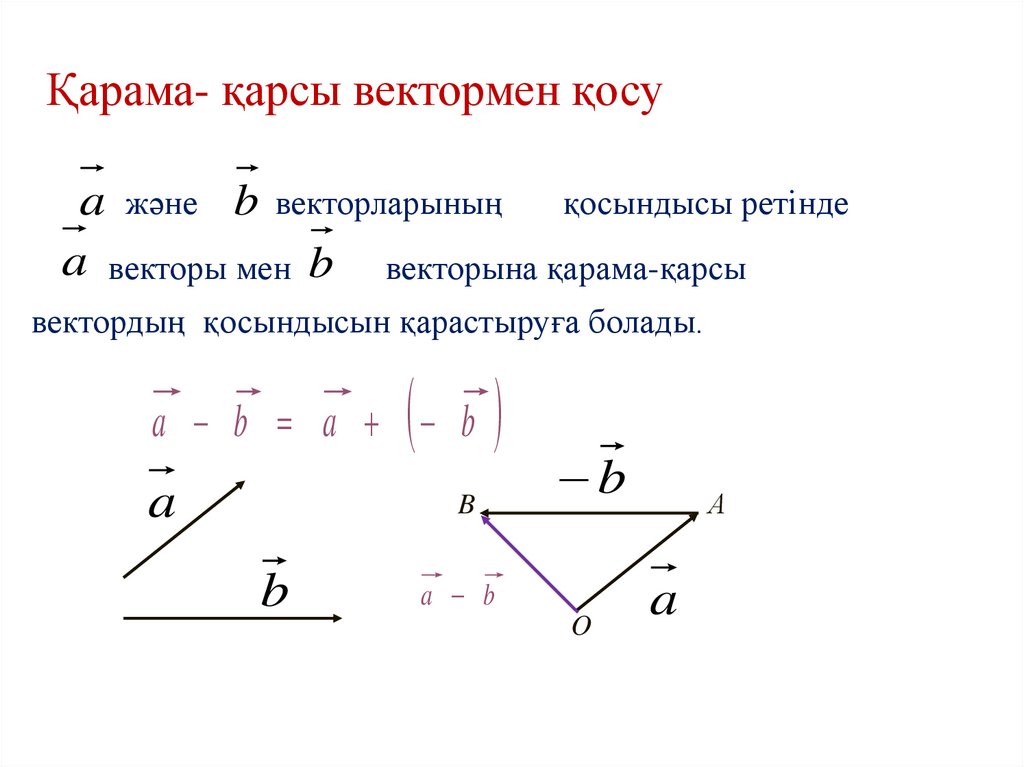
25. Қарама- қарсы вектормен қосу

a және b векторларының қосындысы ретінде
a векторы мен b векторына қарама-қарсы
вектордың қосындысын қарастыруға болады.
a b a b
a
B
b
b
a b
O
А
a

26. Векторды санға көбейту

Нөлдік емес а векторы мен к санының көбейтіндісі
деп, |к|▪ |а| болатын в векторын айтады, егер к> 0
болса, вектор берілген вектормен бағыттас, ал к<0
болса шыққан вектор берілген вектормен қарамақарсы бағытталған болады
a
2a
b
1
b
3

27. Қасиеттері

Нөлдік вектордың кез келген санға
көбейтіндісі нөлдік вектор болып саналады.
0 n 0
Кез келген вектордың нөл санына
көбейтіндісі нөлдік вектор болып саналады.
n 0 0

28. Қасиеттері

Кезкелген a және b векторлары үшін және кез
келген k, l сандар үшін мына теңдіктер орын
алады.
1. (k l)a = k (l a) – көбейтудің терімділік заңы
2. k (a+b) = ka + kb - I- үлестірімділік заңы
3. (k+ l) a = ka + la - II -үлестірімділік заңы

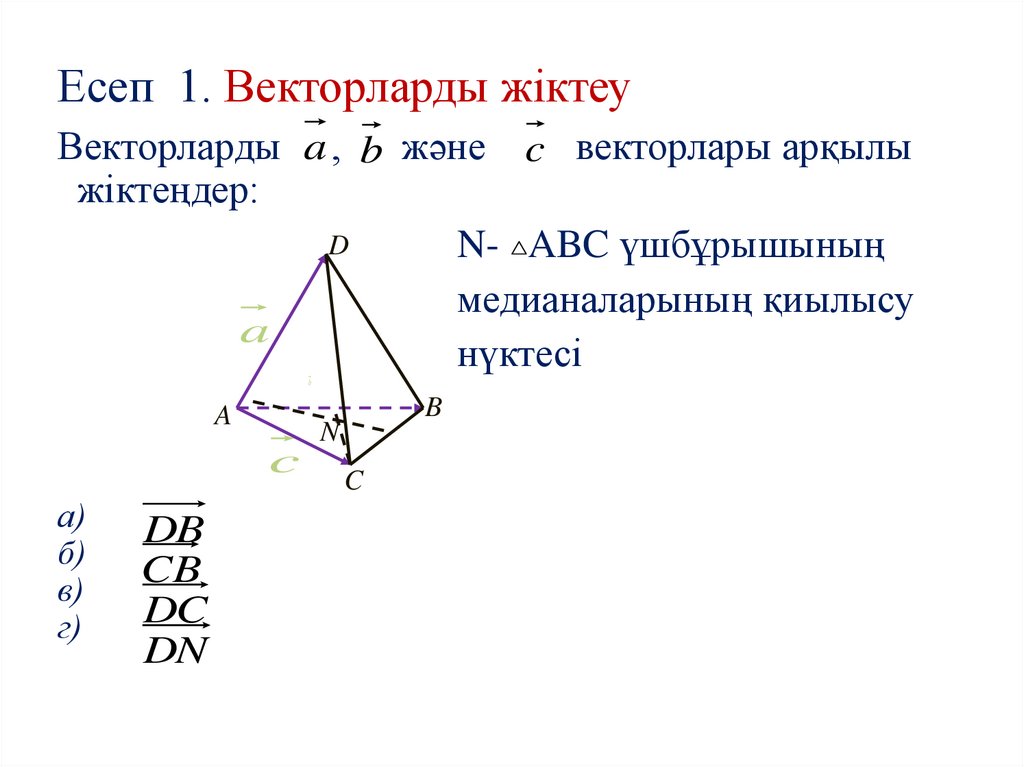
29. Есеп 1. Векторларды жіктеу

Векторларды a , b және c векторлары арқылы
жіктеңдер:
D
N- ABC үшбұрышының
медианаларының қиылысу
a
нүктесі
b
A
N
c
а)
б)
в)
г)
DB
CB
DC
DN
B
C

30. Шешуі

а) DB b a
б)
CB b c
в)
г) DC c a
1
DN a AN a ( b c )
3
1
1
a b c
3
3

31. Есеп 2. Қосу және азайту

Өрнекті ықшамдаңдар:
а) CM MK
б)
в)
г)
д)
е)
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD

32. Шешуі :

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д)
AC BC PM AP BM
AC CB MP PA BM
е)
AB MA BM AM MA 0
AD MP EK EP MD
AD DM MP PE EK
AK

33.

34. Үй жұмысы

35. Рефлексия