Similar presentations:
Алгоритмы сглаживания
1. САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
1.Алгоритмы сглаживания2.Моделирование сигнала датчика
3.Алгоритмы допускового контроля
Куркина
Виктория Вадимовна
2.
Алгоритмическая реализацияинформационных задач.
.
К информационным задачам относится прежде всего опрос
датчиков и последующая обработка данных.
Алгоритмы и программы сбора данных в АСУТП
обеспечивают ввод результатов измерения режимных и
технологических параметров объекта управления в
микропроцессор, ЭВМ или контроллер. Как известно АСУТП
содержит от 10-40 датчиков (малая мощность) до 2500
контролируемых переменных (большая мощность).
Информация о процессе или объекте собирается с датчиков
и записывается в память машины или выдается на любое
средство визуализации – дисплей, мнемосхема, печатное
устройство и т.п.
2
.
Информация с датчиков считывается в режиме циклического
или адресного опроса.
3.
Алгоритмическая реализацияинформационных задач.
.
Алгоритмы первичной обработки.
Вся получаемая с датчиков в АСУТП информация
подвергается первичной обработке, которая
подразумевает:
-определение истинных значений переменных по
показаниям датчиков;
-фильтрация сигналов;
-верификация информации (проверка её на
достоверность), включающая дополнительный
контроль- допусковый и статистический.
3
.
4.
Алгоритмы фильтрации(сглаживания)
Как правило, информация, получаемая с
датчиков содержит
кроме полезного сигнала различные мешающие
факторы:
.
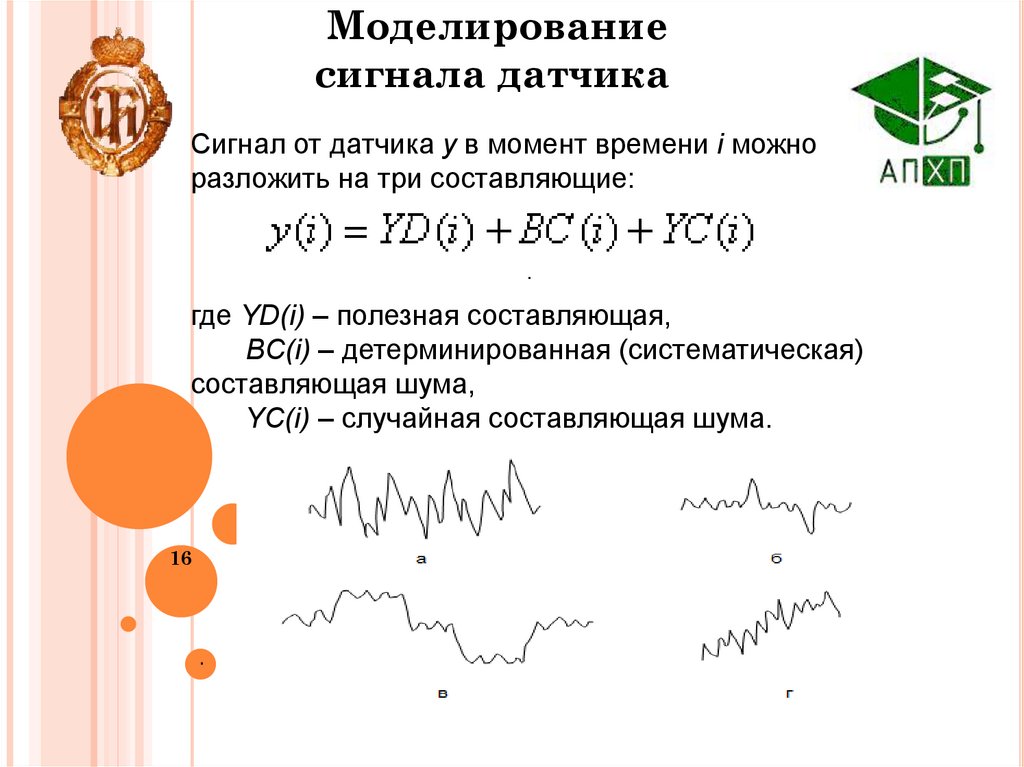
•выбросы (грубые ошибки) (рисунок б);
•импульсные помехи, сдвиги (рисунок в)
•монотонный дрейф (рисунок г);
•повышенный уровень шума (рисунок а);
4
.
5.
Алгоритмы фильтрации(сглаживания)
5
.
Причина появления различных мешающих факторов
– от неисправности в самой измерительной цепи до
неполадок в самом объекте управления (стирание …
в цепи мельницы, обмазка внутри реакторов,
влияние шумов соседних
мельниц, обрушение
.
клинкерного кольца в цепи обжига и т.п.) Однако
информация, получаемая от датчиков, используется
для формирования управляющих воздействий.
Влияние
мешающих
факторов
может
быть
уменьшено либо физически либо программно
реализованным фильтром.
Остановимся на классе линейных фильтров.
Нахождение по оценкам процесса y(t) оценок его
детерминированной составляющей yd(t) и является
задачей операции сглаживания сигнала y(t).
Алгоритмы
сглаживания,
реализующие
определенные математические и эмпирические
методы,
называются
программными
или
цифровыми фильтрами.
6.
Алгоритмы фильтрации(сглаживания)
1.Алгоритм фильтрации методом
экспоненциального сглаживания.
.
2. Алгоритм фильтрации методом
скользящего и скачущего среднего
(арифметического среднего).
3 Алгоритм фильтрации методом
медианы.
6
.
Рассмотрим каждый из них.
7.
Алгоритм фильтрации методомэкспоненциального сглаживания.
.
7
.
8.
Алгоритм фильтрации методом скользящегосреднего (арифметического среднего).
.
8
.
Характеристиками фильтра являются : объём выборки В
и способ формирования выборки- скачущая или
скользящая.
9.
Алгоритм фильтрации методом медианы..
9
.
10.
Алгоритмы фильтрации(сглаживания)
1.Алгоритм фильтрации методом
экспоненциального сглаживания.
.
2. Алгоритм фильтрации
методом
скользящего и скачущего среднего
(арифметического среднего).
3 Алгоритм фильтрации методом
10
медианы.
.
11.
Алгоритмы фильтрации(сглаживания)
Сравним 3 рассмотренных фильтра:
.
11
.
12.
Алгоритмы фильтрации(сглаживания)
Сравним 3 рассмотренных фильтра:
Экспоненциальн
ый
Среднего
арифметического
Медианы
12
Достоинства
простота реализации;
давит
частоты;
Недостатки
искажение входного сигнала
высокие
.
отношение
cигнал/шум
увеличивает в 3-4
раза.
значительно
при
использовании
скач.
подавляет шумовую выборки
входной
сигнал
составляющую;
сильно скажается (мало точек
на выходе фильтра);
прост. в реализации.
плохо работает с сигналом,
содержащим
импульсные
помехи и выбросы.
меньше
искажение требует
ранжирования
сигнала;
элементов выборки;
давит
импульсные сложнее
в
помехи и выбросы.
реализации;
программной
пропускает много шумов;
работает хуже, чем ср.ар.
.
Рассмотрим представление алгоритмов сглаживания в
различных формах.
13.
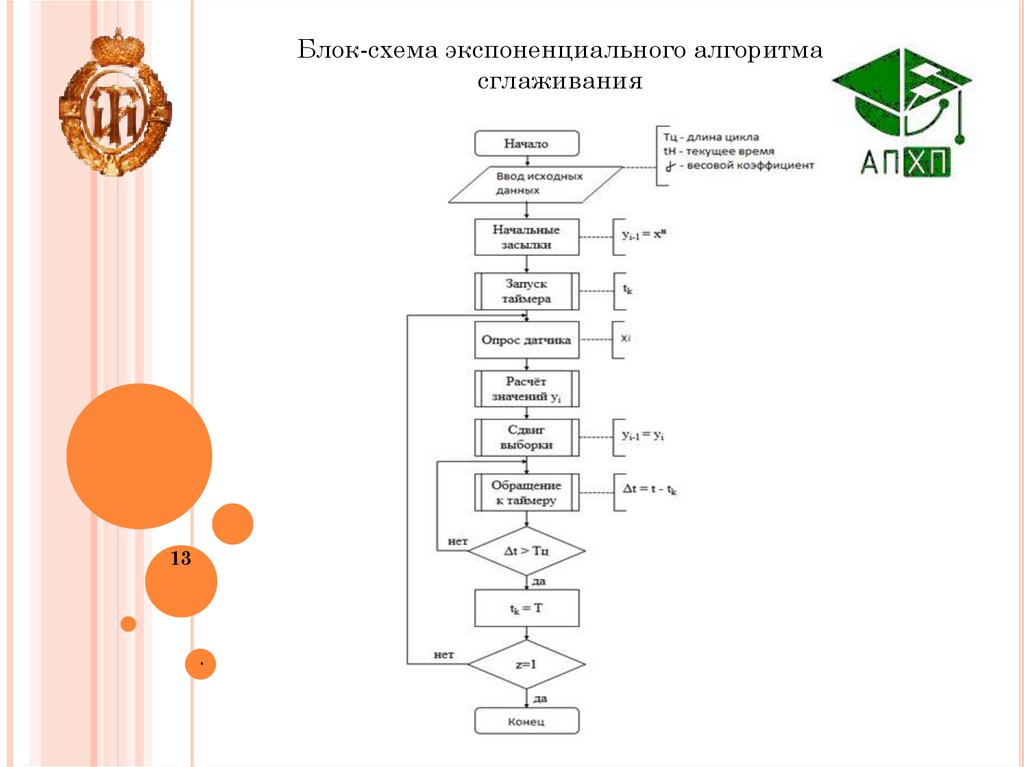
Блок-схема экспоненциального алгоритмасглаживания
.
13
.
14.
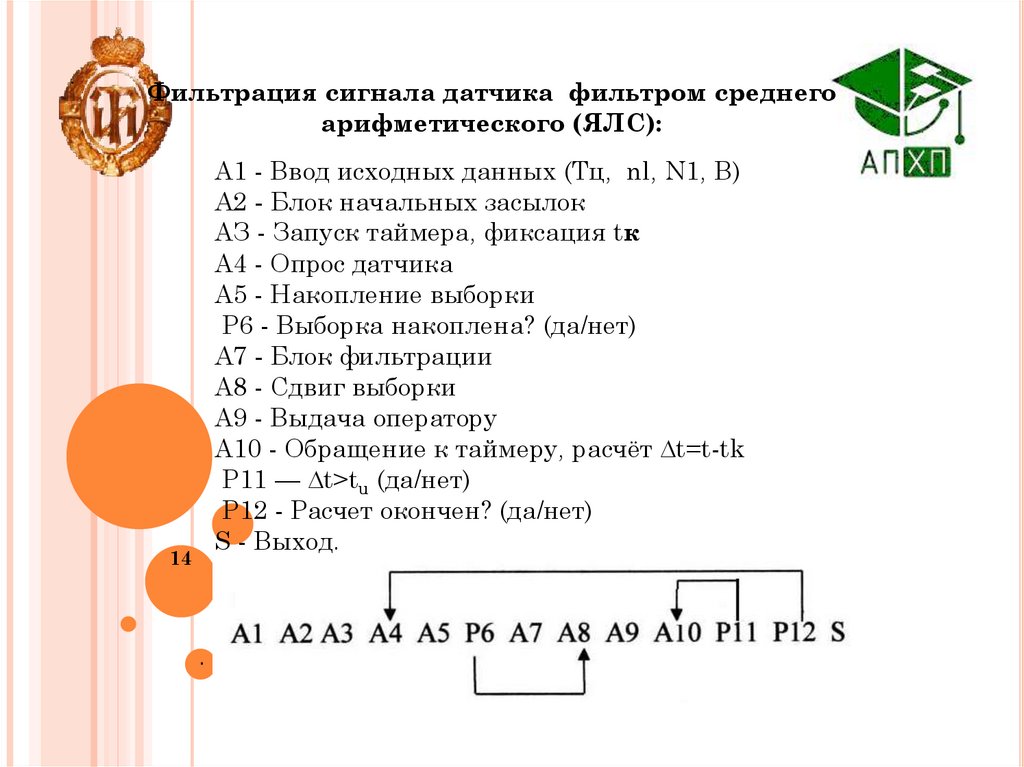
.Фильтрация сигнала датчика фильтром среднего
арифметического (ЯЛС):
А1 - Ввод исходных данных (Тц, nl, N1, В)
А2 - Блок начальных засылок
АЗ - Запуск таймера, фиксация tк
А4 - Опрос датчика
А5 - Накопление выборки
P6 - Выборка накоплена? (да/нет)
А7 - Блок фильтрации
А8 - Сдвиг выборки
А9 - Выдача оператору
А10 - Обращение к таймеру, расчёт t=t-tk
P11 — t>tu (да/нет)
P12 - Расчет окончен? (да/нет)
S - Выход.
14
.
15.
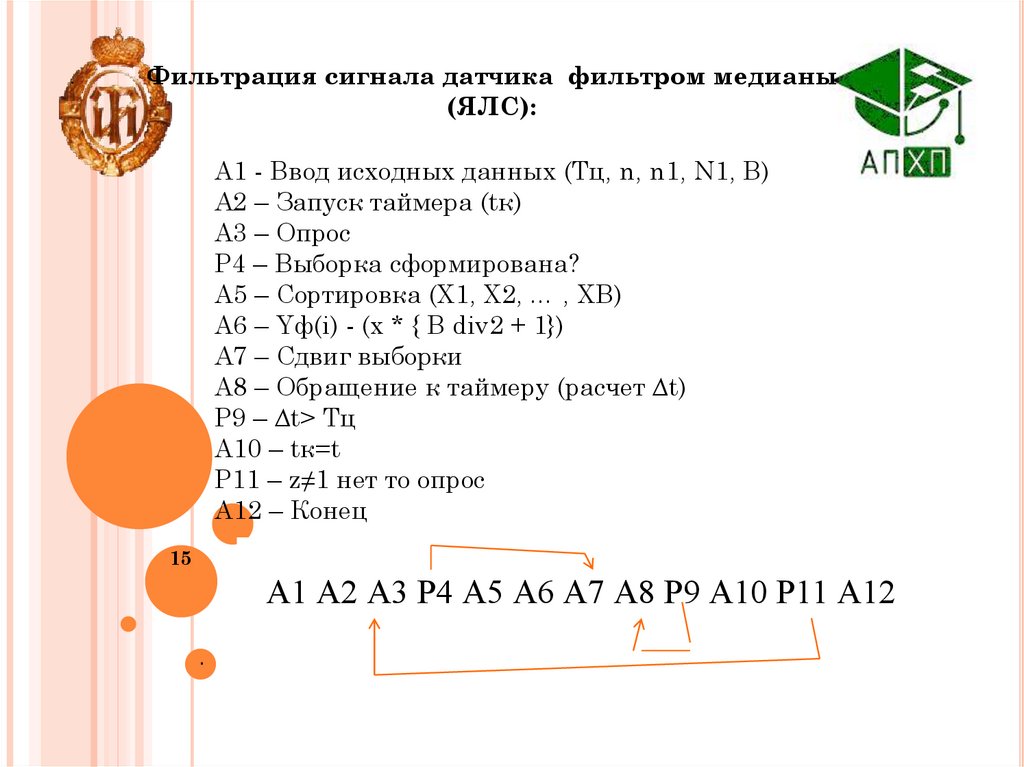
.Фильтрация сигнала датчика фильтром медианы
(ЯЛС):
А1 - Ввод исходных данных (Тц, n, n1, N1, B)
А2 – Запуск таймера (tк)
А3 – Опрос
P4 – Выборка сформирована?
A5 – Сортировка (X1, X2, … , XВ)
A6 – Yф(i) - (x * { В div2 + 1})
А7 – Сдвиг выборки
А8 – Обращение к таймеру (расчет ∆t)
Р9 – ∆t> Тц
А10 – tк=t
P11 – z≠1 нет то опрос
А12 – Конец
15
А1 А2 А3 Р4 А5 А6 А7 А8 Р9 А10 Р11 А12
.
16.
Моделированиесигнала датчика
Сигнал от датчика y в момент времени i можно
разложить на три составляющие:
.
где YD(i) – полезная составляющая,
BC(i) – детерминированная (систематическая)
составляющая шума,
YC(i) – случайная составляющая шума.
16
.
17.
Моделированиесигнала датчика
Полезная составляющая выражается формулой
,
где С – постоянное число
Детерминированная составляющая может представлять
собой либо сдвиг:
либо монотонный дрейф :
17
где bi – время начала действия систематической
составляющей шума, V – величина сдвига, k –
коэффициент дрейфа.
18.
Моделированиесигнала датчика
Случайная составляющая может быть как нормально
распределённым шумом: ,
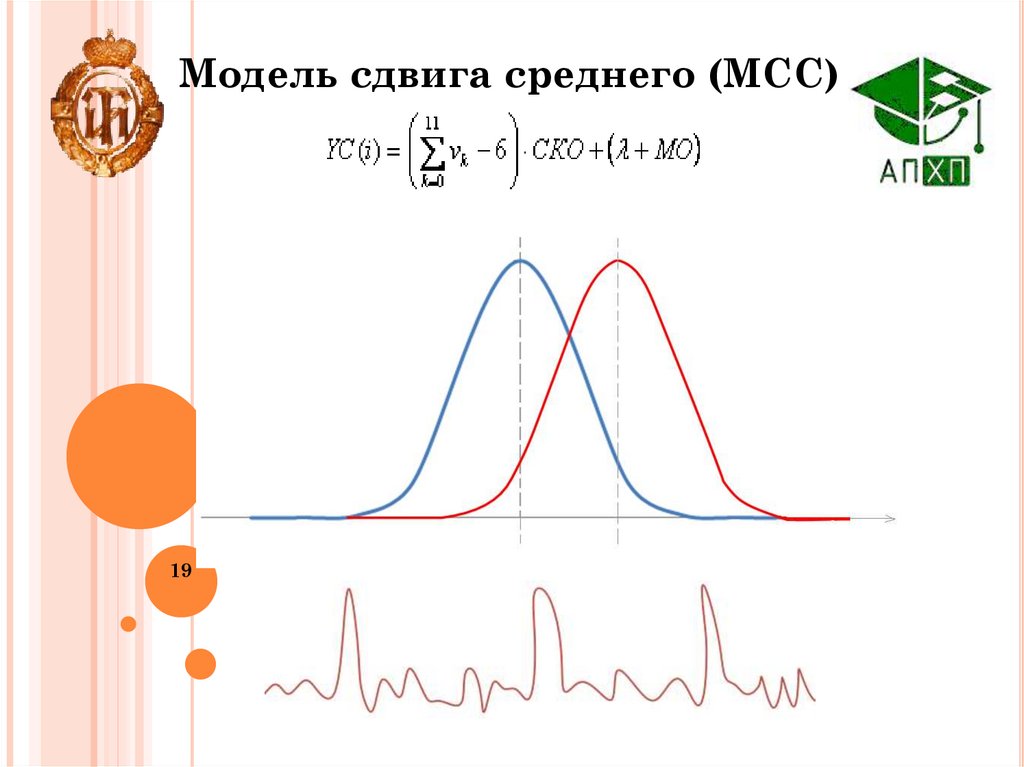
так и шумом с выбросами по модели сдвига среднего:
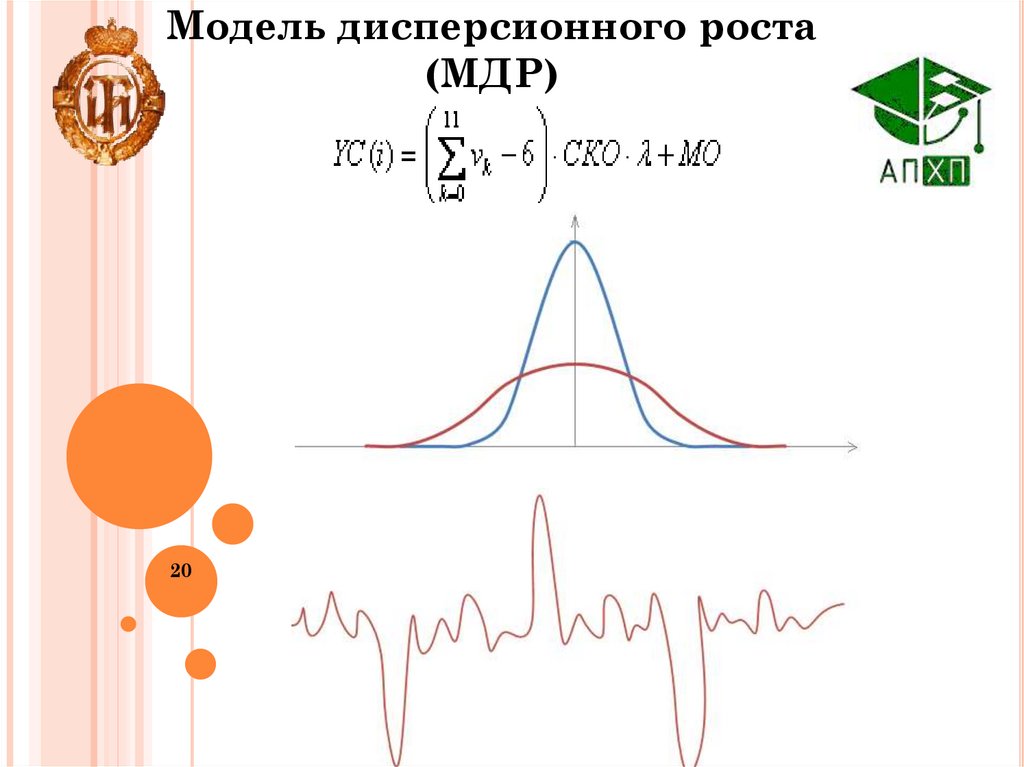
или шумом с выбросами по модели дисперсионного
роста
18
где СКО – среднеквадратическое отклонение, МО –
математическое ожидание, λ – величина,
характеризующая величину сдвига МО или изменения
СКО нормального шума. vk – равномерно
распределённая случайная величина в диапазоне от 0
до 1.
19.
Модель сдвига среднего (МСС)19
20.
Модель дисперсионного роста(МДР)
20
21.
Алгоритм моделированиясигнала датчика
Введем следующие обозначения:
n-общее число точек,
.
SG-среднеквадратическое
отклонение,
M0-математическое ожидание,
PV- вероятность выбросов,
- параметр формирования выбросов,
Кв-коэффициент дрейфа.
21
.
Если m=0, дрейфа нет.
Если k=0, выбросов нет
Если k=1, то это модель сдвига среднего
Если k=2,то это модель дисперсионного роста.
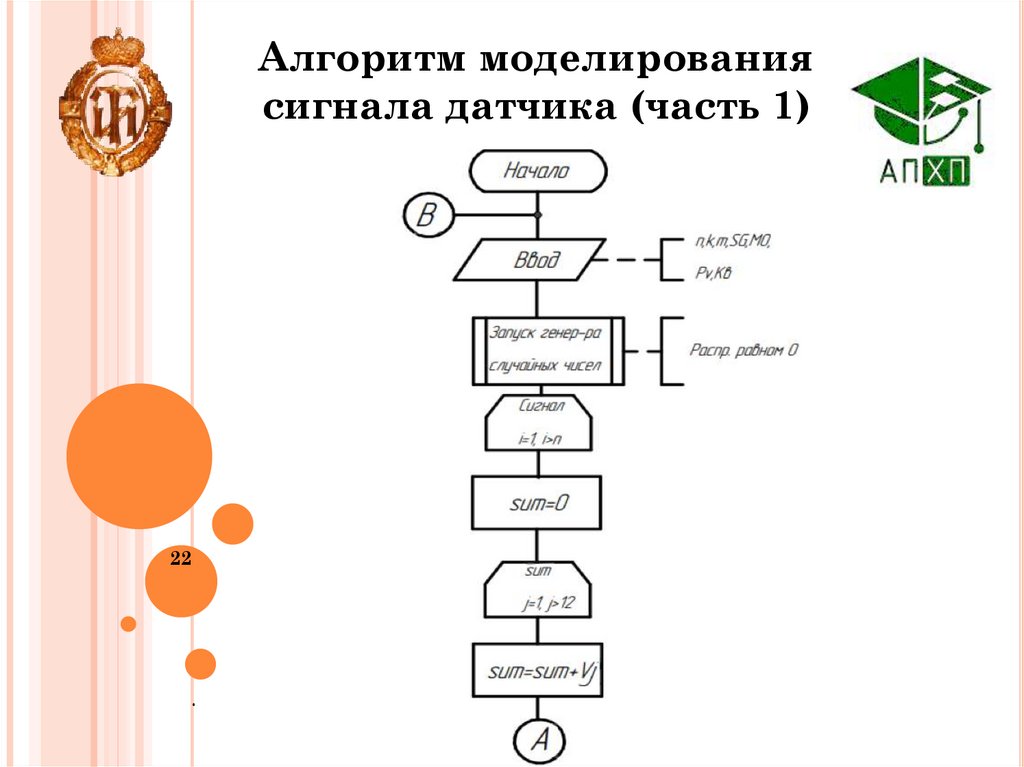
22.
Алгоритм моделированиясигнала датчика (часть 1)
.
22
.
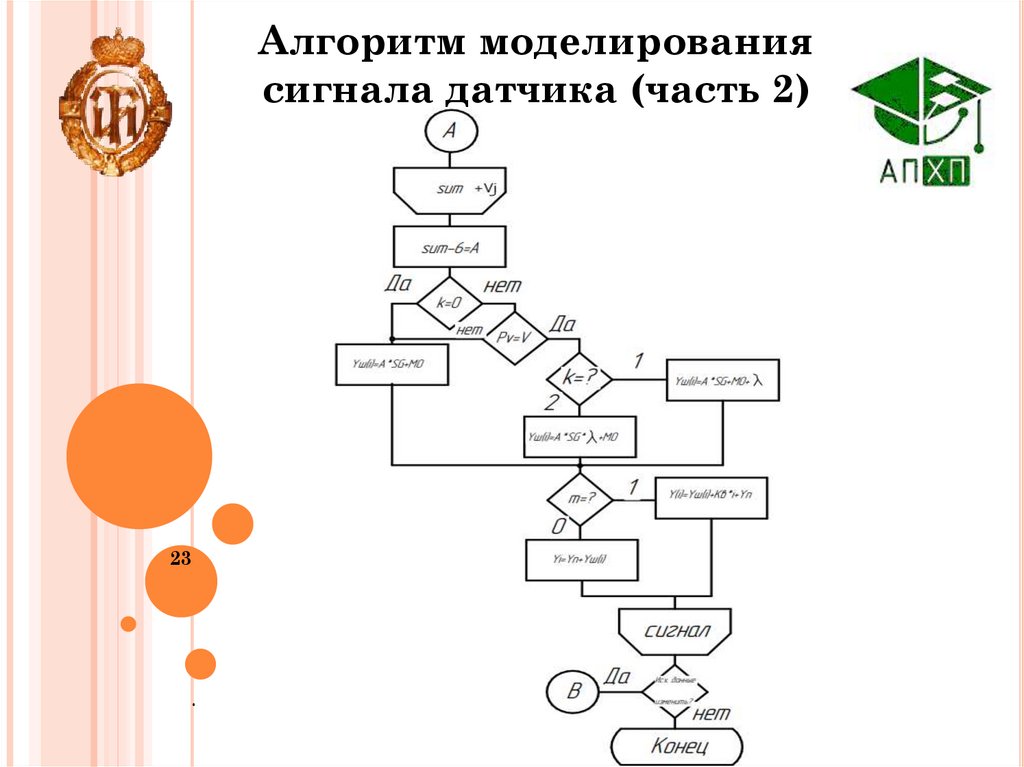
23.
Алгоритм моделированиясигнала датчика (часть 2)
.
23
.
24.
Нормальное распределениеНепрерывная случайная величина X имеет нормальный
закон распределения (закон Гаусса) с параметрами α и β,
если ее плотность вероятности имеет вид:
.
24
.
Где:
β — среднеквадратичное
отклонение (σ);
α — среднее (М);
e, π - константы
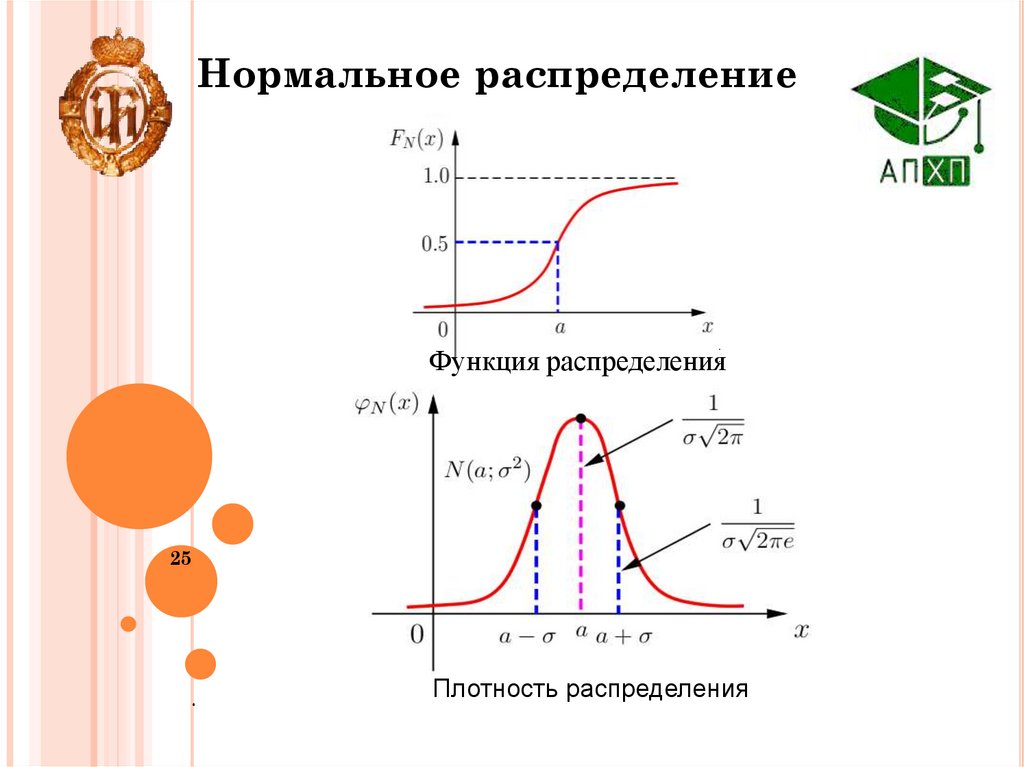
25.
Нормальное распределение.
Функцияраспределения
распределени
Функция
25
.
Плотность распределения
26.
Свойства нормальногораспределения
Правило 3 сигм (99,72% значений лежат в
рамках M+/-3σ)
.
26
.
Распределение симметрично (А=0), эксцесс
(мера остроты пика) Е = 0
Мода, медиана и среднее совпадают
Значения, лежащие на равном расстоянии от M
(среднего), имеют равную частоту в выборке
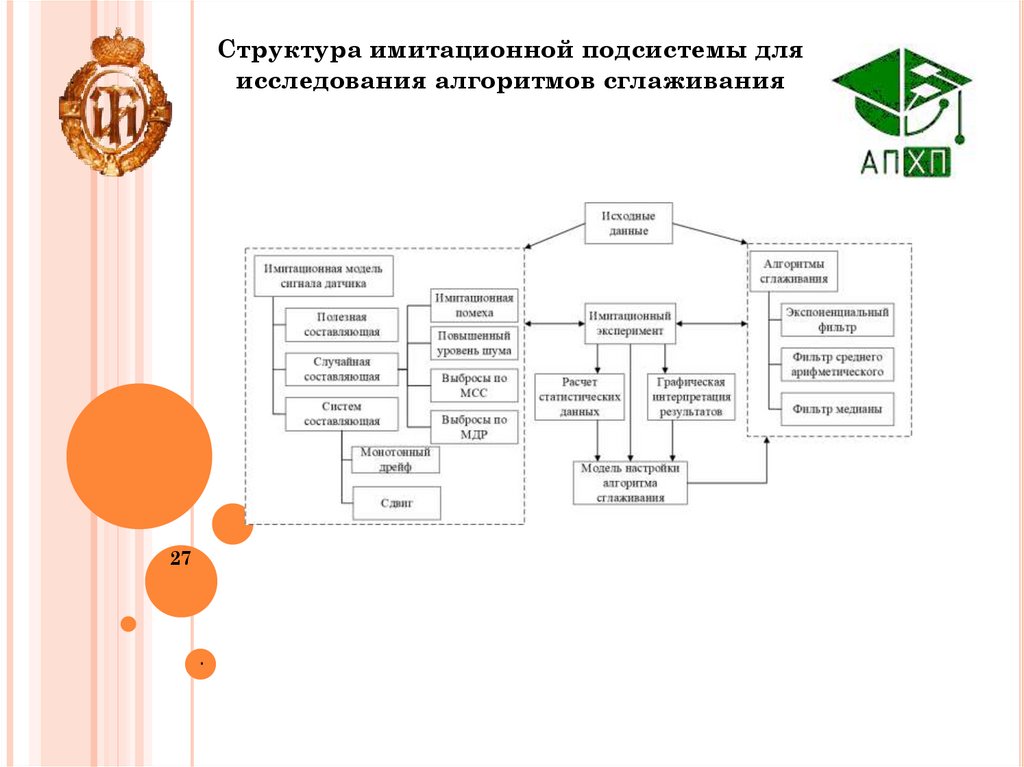
27.
Структура имитационной подсистемы дляисследования алгоритмов сглаживания
.
27
.
28.
Алгоритмы контроля достоверностиизмерительной информации
Понятие достоверности
1 Достоверность - это характеристика знаний как
обоснованных, доказанных, истинных.
2 Достоверность – это свойство информации
отражать реально существующие объекты с необходимой
точностью.
3 Под достоверностью понимается свойство
информации давать сведения характеризующиеся
погрешностями, не выходящими за пределы допустимых
значений.
28
4 Достоверность измерений – это показатель
степени доверия к результатам измерения, то есть
вероятность отклонений измерения от действительных
значений.
29.
Алгоритмы контроля достоверностиизмерительной информации
5 Достоверность может быть определена численно,
следуя следующему определению:
Достоверность –
это вероятность отсутствия в измерительной
информации аномальных ошибок различного рода.
D = 1 – Pош.
Здесь Pош – вероятность аномальной ошибки.
К аномальным ошибкам относятся: выбросы,
монотонный дрейф, сдвиги, искажения формы пика.
Точность измерения – это свойство, которое
29 отображает близость результатов измерений к
истинным значениям измеряемых величин.
Точность измерений – степень приближения
измерения к действительному значению величины
30.
Алгоритмы контролядостоверности
измерительной информации
Для контроля достоверности результатов
измерения используют:
алгоритмы допускового контроля и
алгоритмы статистического контроля.
В алгоритмы допускового контроля
входят:
а) алгоритм отбраковки информации по
диапазону возможных изменений;
30
б) алгоритм отбраковки информации по
диапазонам изменения переменной и по ее
производной.
Рассмотрим их подробнее.
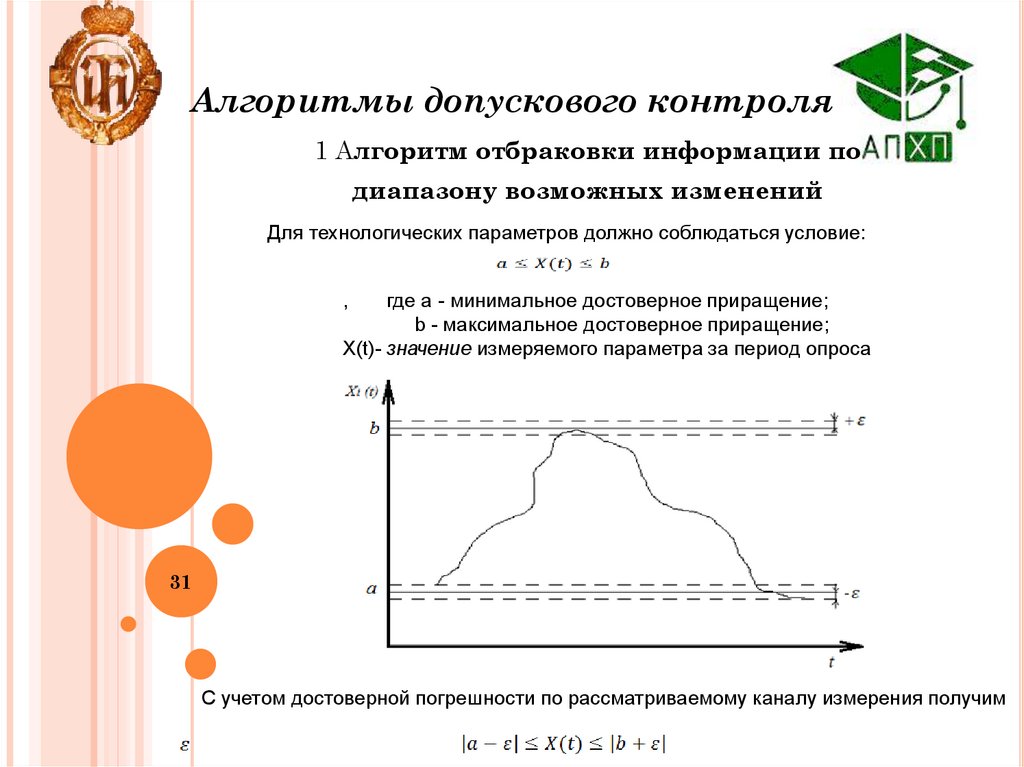
31.
Алгоритмы допускового контроля1 Алгоритм отбраковки информации по
диапазону возможных изменений
Для технологических параметров должно соблюдаться условие:
,
где а - минимальное достоверное приращение;
b - максимальное достоверное приращение;
Х(t)- значение измеряемого параметра за период опроса
31
С учетом достоверной погрешности по рассматриваемому каналу измерения получим
32.
Алгоритмы допусковогоконтроля
2 Алгоритм отбраковки информации по
диапазонам изменения переменной и по ее
производной
,
Для технологических параметров должны соблюдаться условия допускового контроля:
где
- скорость изменения измеряемого параметра за период
опроса,
с- минимальное достоверное приращение при двух
последовательных опросах,
d - максимальное достоверное приращение,
t - период опроса
32
Итоговая формула для проверки скорости изменения:
Здесь с- ∆Хмин,
d-∆Хмах
Допусковая проверка может быть организована для всех измеряемых
аналоговых параметров.
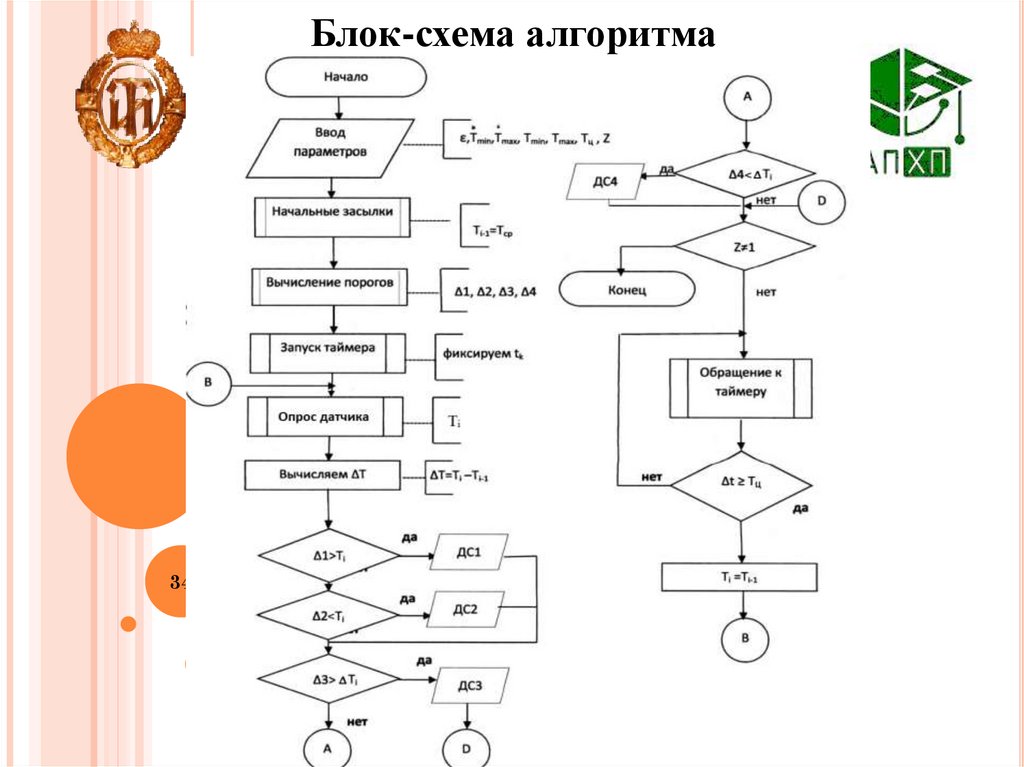
33.
Допусковый контроль текущего значениясигнала датчика и скорости его изменения в виде
блок-схемы
В алгоритме допускового контроля рассчитываются
следующие пороги:
l=Xmin-
2=Xmax+
3= Xmax+2
4= Xmin-2
В качестве измеряемого параметра рассматривается
канал измерения температуры Т.
Результат каждой проверки представляется
диагностическим сообщением оператору
ДС1, ДС2, ДС3, ДС4.
Для работы алгоритма необходимо ввести:
Тmin, Тmax, Тmin , Тmax, , дискретность опроса Тц,
33
признак окончания алгоритма Z/
34.
Блок-схема алгоритма34
35.
Фрагмент алгоритмаобнаружения искажения типа
«асимметрия»
35
36.
Спасибо за внимание36























 informatics
informatics








