Similar presentations:
Красота в графиках. Логарифмическая спираль
1. Красота в графиках
2. Логарифмическая спираль
Возрастающая кривая, укоторой касательная в
каждой точке образовывает с
радиус-вектором в каждой
точке всегда один и тот же
угол. Полярные углы для точек
кривой пропорциональны
логарифмам радиусвекторов. Отсюда и название:
логарифмическая спираль.
Расстояние между витками
растет с увеличением угла, т.
е. радиус-вектор
увеличивается
экспоненциального с
увеличением угла поворота.
3.
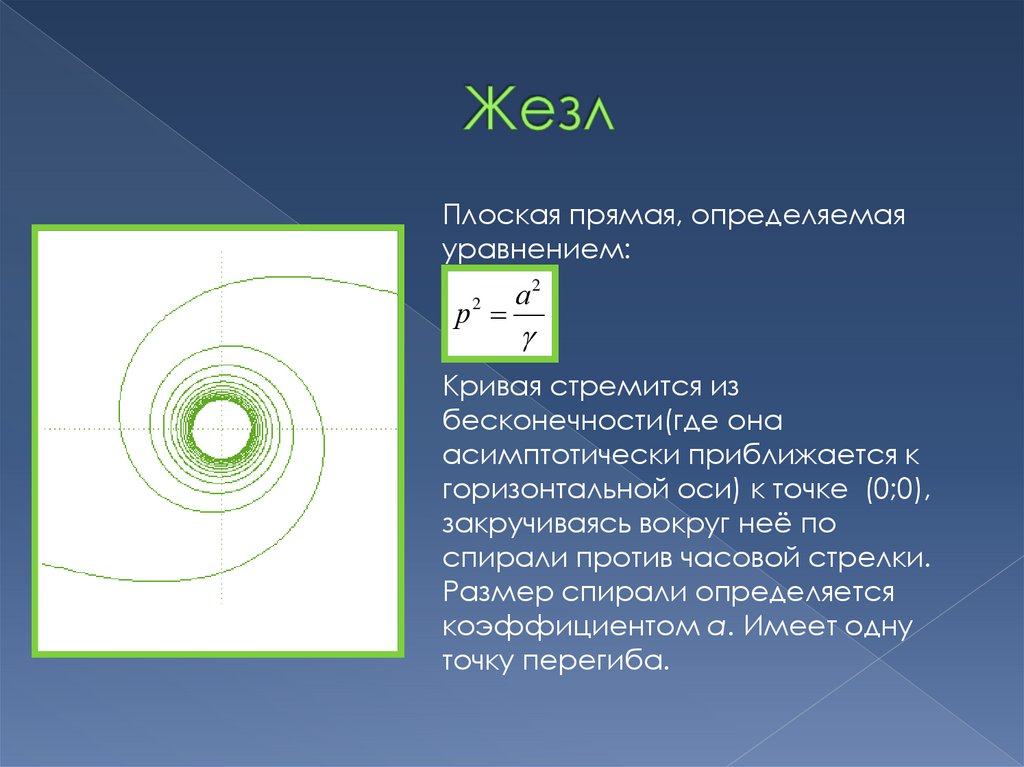
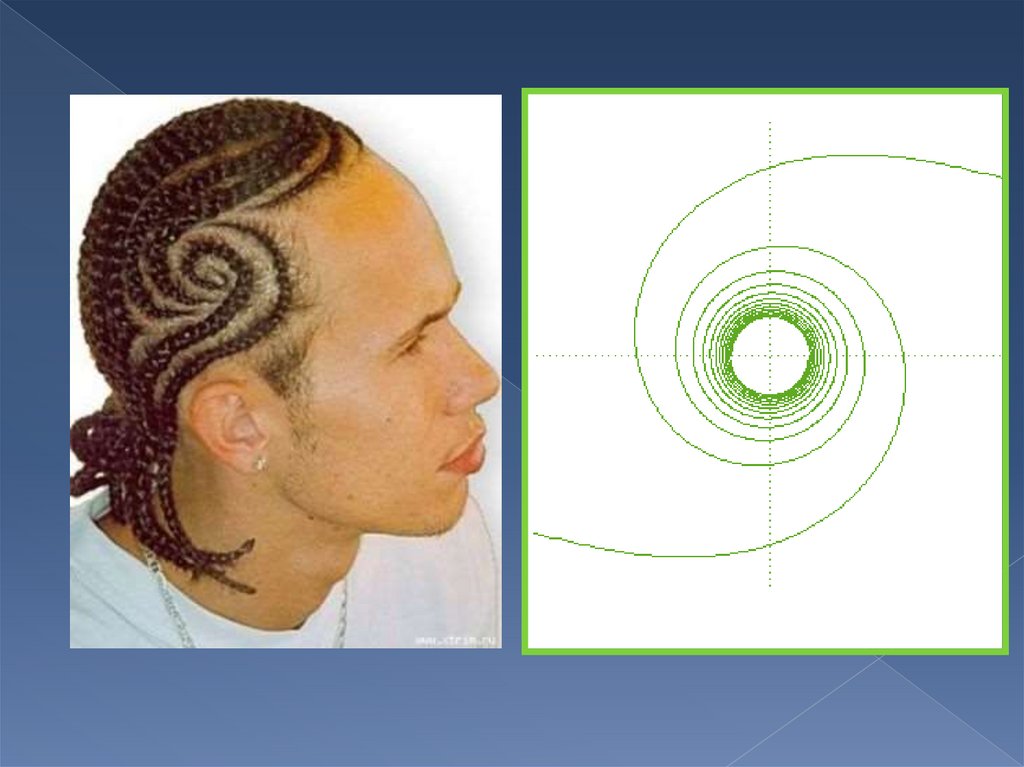
4. Жезл
Плоская прямая, определяемаяуравнением:
р
2
а2
Кривая стремится из
бесконечности(где она
асимптотически приближается к
горизонтальной оси) к точке (0;0),
закручиваясь вокруг неё по
спирали против часовой стрелки.
Размер спирали определяется
коэффициентом а. Имеет одну
точку перегиба.
5.
6. Улитка паскаля
Плоская алгебраическаякривая 4-го порядка; подера
окружности, конхоида
окружности относительно
точки на окружности,
частный случай Декартова
овала, она также является
эпитрохоидой. Названа по
имени Этьена Паскаля (отца
Блеза Паскаля), впервые
рассмотревшего её.
Три улитки паскаля, конхоиды чёрной
l<2r, красная
l=2r и синяя l>2r
окружности: зелёная
(кардиоида)
p 2r cos l
7.
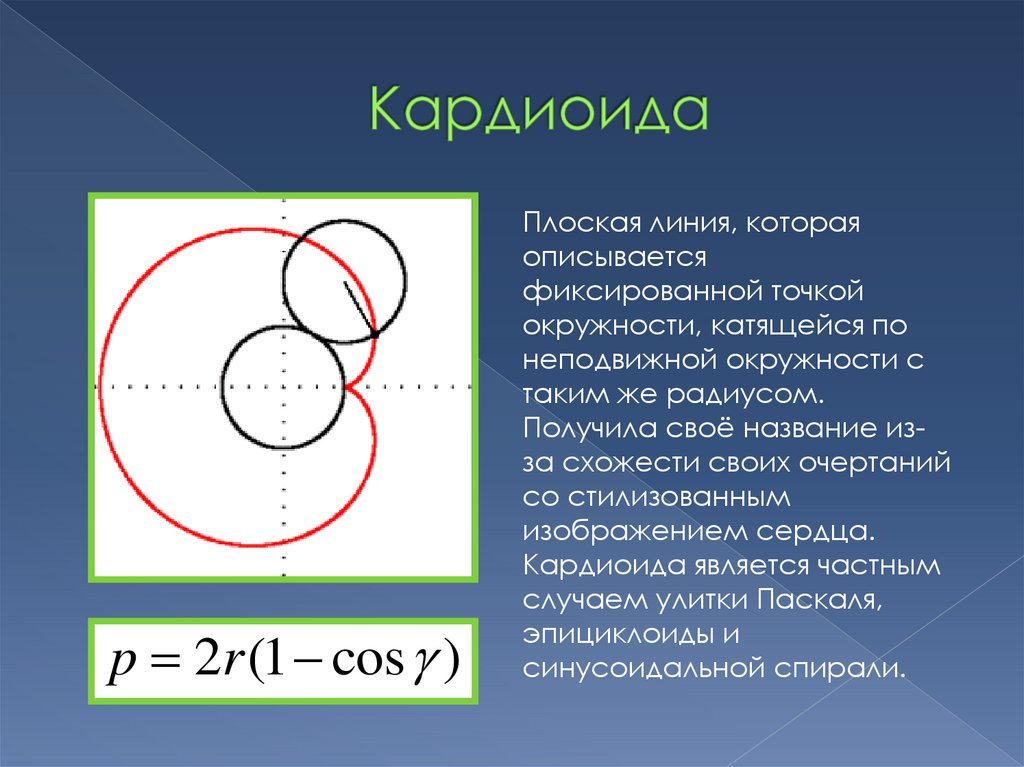
8. Кардиоида
p 2r (1 cos )Плоская линия, которая
описывается
фиксированной точкой
окружности, катящейся по
неподвижной окружности с
таким же радиусом.
Получила своё название изза схожести своих очертаний
со стилизованным
изображением сердца.
Кардиоида является частным
случаем улитки Паскаля,
эпициклоиды и
синусоидальной спирали.
9.
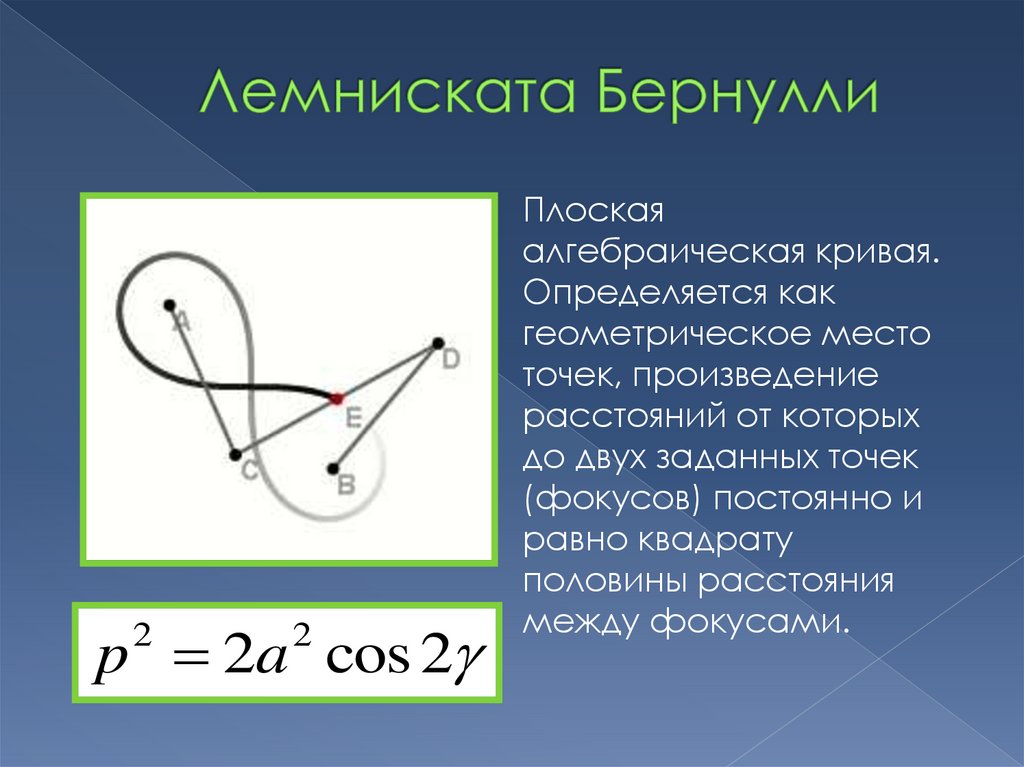
10. Лемниската Бернулли
p 2a cos 22
2
Плоская
алгебраическая кривая.
Определяется как
геометрическое место
точек, произведение
расстояний от которых
до двух заданных точек
(фокусов) постоянно и
равно квадрату
половины расстояния
между фокусами.
11.
12. Каппа
p actg13. Эллипс
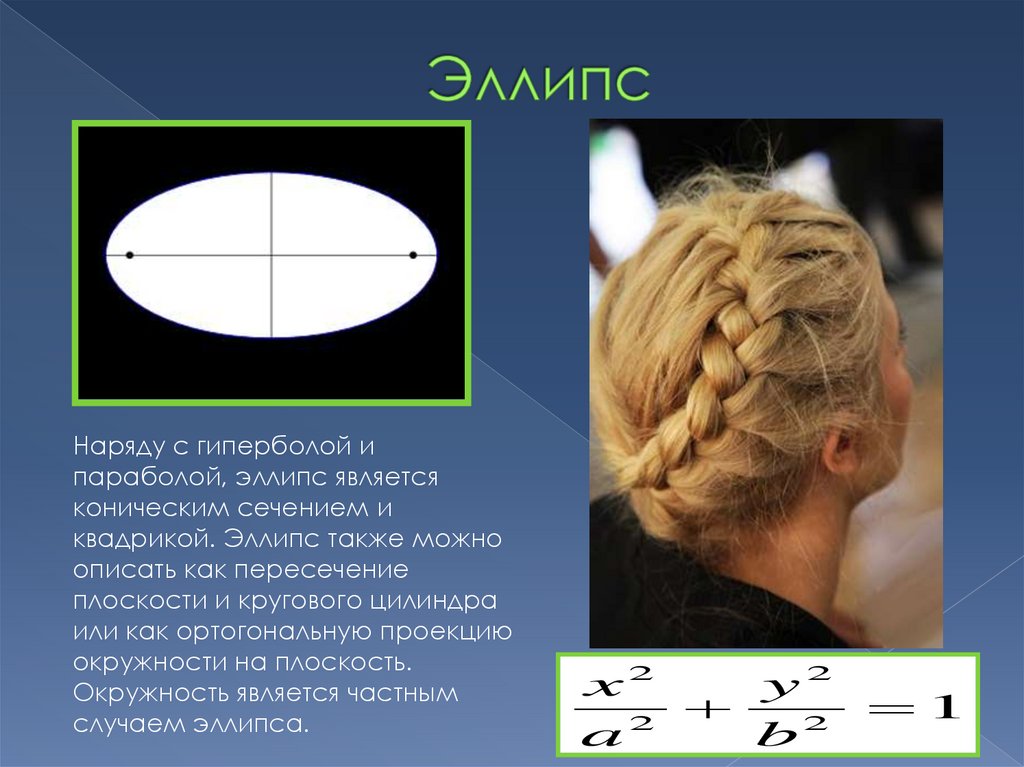
Наряду с гиперболой ипараболой, эллипс является
коническим сечением и
квадрикой. Эллипс также можно
описать как пересечение
плоскости и кругового цилиндра
или как ортогональную проекцию
окружности на плоскость.
Окружность является частным
случаем эллипса.
x2
y2
1
2
2
a
b
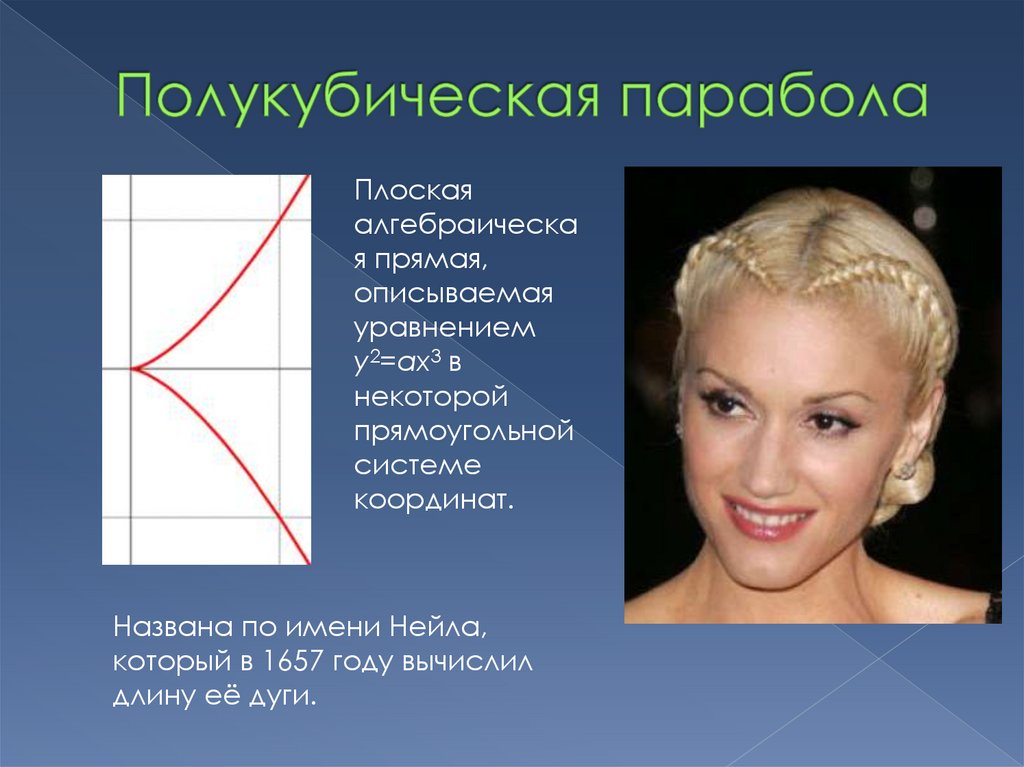
14. Полукубическая парабола
Плоскаяалгебраическа
я прямая,
описываемая
уравнением
y2=ax3 в
некоторой
прямоугольной
системе
координат.
Названа по имени Нейла,
который в 1657 году вычислил
длину её дуги.
15. Овал Кассини
Геометрическое место точек,произведение расстояний от которых
до двух заданных точек (фокусов)
постоянно и равно квадрату
некоторого числа а.
x y 2c x y a c 0
2
2
2
2
2
4
4









 mathematics
mathematics








