Развитие интеллектуально-творческой деятельности учащихся при обучении математике на этапе предпрофильной подготовки

1. Развитие интеллектуально-творческой деятельности учащихся при обучении математике на этапе предпрофильной подготовки

Развитие
интеллектуальнотворческой деятельности
учащихся при обучении
математике на этапе
предпрофильной
подготовки
Специальность: 13.00.02. — теория и
методика обучения и воспитания
(математика, уровень общего образования)

2.

Объект исследования - ИТД
учащихся старшего школьного
возраста, реализуемая в процессе
обучения математике.
Предмет исследования – средства и
условия развития ИТД учащихся в
процессе обучения математике в
рамках предпрофильной подготовки.
Цель исследования – разработка
методики развития ИТД учащихся
старшего школьного возраста при
обучении математике в рамках
предпрофильной подготовки.

3. Гипотеза исследования

Педагогическое взаимодействие в
процессе обучения математике будет
способствовать развитию ИТД учащегося,
если в основе методики обучения будет
лежать:
использование открытых математических
заданий разной степени
неопределенности, предполагающих
интеграцию математических знаний в ходе
их выполнения,
создание соответствующей им
организационно-методической ситуации,
сочетающей различные виды
индивидуальной и групповой деятельности
учащихся.

4. На защиту выносятся следующие положения

1.
Актуальным направлением
совершенствования методики
обучения математике является
создание средств, а также
содержательных и
организационных условий,
обеспечивающих становление
интеллектуально-творческой
деятельности как наивысшей формы
проявления самостоятельной
учебно-познавательной
деятельности учащихся.

5.

2. Содержательным условием развития
ИТД учащихся при обучении
математике является интеграция
математического содержания.
Организационным условием
становления ИТД учащихся при
обучении математике является
интегративный курс, который может
быть реализован как элективный в
системе предпрофильной
подготовки.

6.

3. Средством развития ИТД являются
открытые математические задания с
разной степенью неопределенности,
которые делятся на определенные,
полуопределенные и
неопределенные. Открытые задания
должны удовлетворять шести
требованиям: наличие смыслового
контекста, проблемность,
неопределенность, доступность,
связь с курсом математики,
интегративность. Способ
конструирования открытых заданий.

7.

4. Организация процесса развития ИТД
учащихся при обучении математике требует
гибкого взаимодействия учителя и учащихся.
Исходя из уровня владения ИТД конкретным
учащимся, учитель должен изменять
интеллектуальную и творческую нагрузку
(потенциал) предлагаемых ему открытых
заданий, создавая педагогические ситуации
ориентировки, поиска, преобразования и
интеграции. Каждой из выделенных
педагогических ситуаций должна
соответствовать форма организации работы
учащихся (индивидуальная, парная,
групповая, индивидуальная) и открытые
задания с заданной степенью
неопределенности (определенные,
полуопределенные, неопределенные),
которые должны преимущественно
использоваться.

8.

интеллектуально-творческая
деятельность - особая форма
активного взаимодействия субъекта с
окружающей действительностью,
направленная на познание,
осознание и преобразование
последней и самого себя, включая
способность к развитию
деятельности.

9. Интеграция математического содержания

предполагает объединение в
целое различных элементов
математического содержания,
рост взаимосвязей и
взамопроникновения между
ними, а также рост
взаимосвязей математических
знаний с другими областями
знаний

10. Направления раскрытия общекультурной составляющей математического содержания

Выявление и раскрытие математических
законов мироздания;
Реализация исторической линии в математике;
Реализация эстетического потенциала
математики;
Реализация практического значения математики в
повседневной жизни;
Выявление связи математики с другими областями
знаний;
Реализация роли математики в формировании
культуры речи;
Выделение и систематизация приемов и методов
школьной
математики;
Интеграция культурных, нравственных ценностей
в содержание предмета.

11. Интегративный курс по математике

учебный курс, строящийся на основе
расширенного по отношению к
приведенному в программе
(государственному образовательному
стандарту) математическому
содержанию, широко реализующего
как внутрипредметные, так и
межпредметные связи математики,
технология освоения которого
учащимися предполагает достижение
образовательного результата
общекультурного характера.

12. Подходы к конструированию интегративных курсов по математике

Теоретический подход
Компетентностный подход

13. Расширение определения понятия «Симметрия»

Неизменность геометрического объекта
по отношению к каким-то
геометрическим преобразованиям,
выполняемым над ним (или совмещение
фигуры при определенного рода
геометрических преобразованиях).
Неизменность какого-либо объекта при
определенного рода преобразованиях.
Общенаучная философская категория,
характеризующая структуру организации
систем.

14. Открытые задания по математике

такие отдельные задания (серия заданий),
которые:
направлены на расширение знаний учащихся
о математических фактах или способах действий
по их установлению;
предполагают возможность получения
нескольких вариантов ответов, среди которых
могут быть уникальные;
содержат условия для проявления
индивидуальных способностей учащихся.

15. Требования, предъявляемые к открытым заданиям

Наличие смыслового контекста
Проблемность
Неопределенность
Доступность
Связь с курсом математики
Интегративность

16. Неопределенность

Открытость условия
Многовариантность
(отсутствие однозначного
решения
алгоритма выполнения
задания или
возможность ученика
самостоятельно открыть
какой-либо факт,
правило или, если способ
решения задания
неизвестен ученику)

17. Направления изменения степени неопределенности задания

Увеличение степени интеллектуального
потенциала задания;
Увеличение степени творческого
потенциала задания;
подбор различных заданий разной
степени неопределенности, но
связанных между собой ключевой
проблемой, которая лежит в их основе.

18. Серия заданий на нахождение фигур, обладающих симметрией квадрата

1) Нарисуйте фигуры того же класса
симметрии, что и класс симметрии
квадрата;
2) Разработайте алгоритм
изображения фигуры, которая
обладает симметрией квадрата.

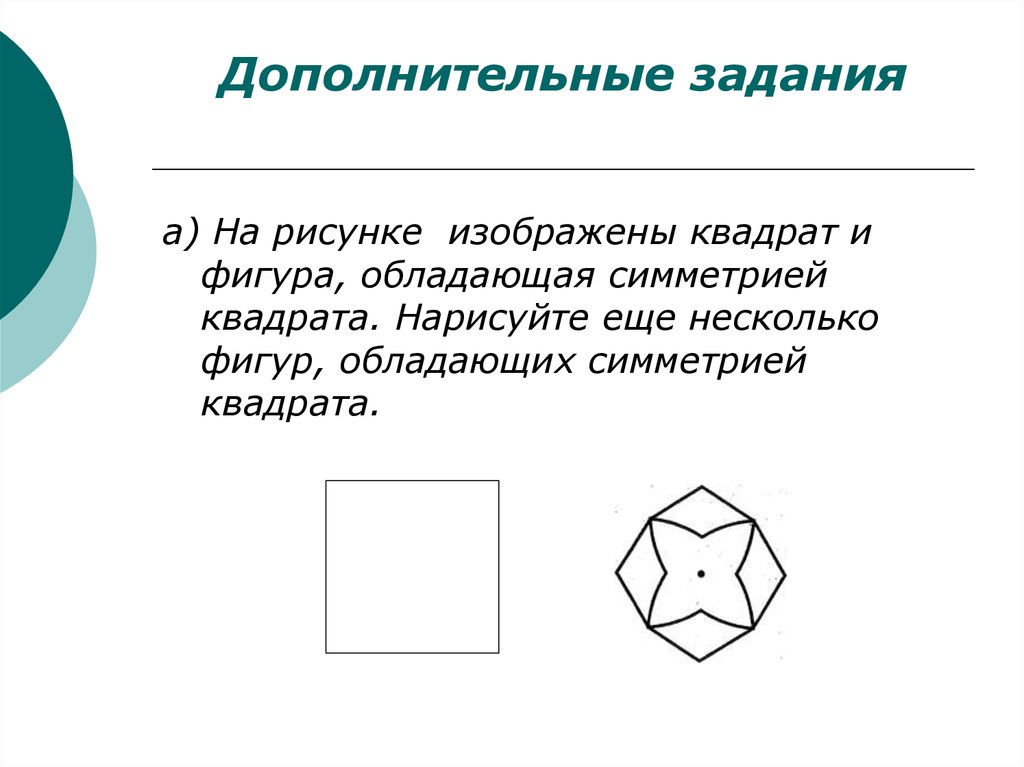
19. Дополнительные задания

а) На рисунке изображены квадрат и
фигура, обладающая симметрией
квадрата. Нарисуйте еще несколько
фигур, обладающих симметрией
квадрата.

20.

б) Среди фигур, изображенных на
рисунке, выберите те из них, которые
обладают симметрией квадрата.

21. При конструировании открытых заданий можно основываться на следующей последовательности действий:

Выбрать понятие (закон, свойство), которое
необходимо изучить;
Выявить различные взаимосвязи данного
понятия как внутри предмета, так и вне его;
Выбрать тот объект, который позволит открыть
(изучить, исследовать) необходимое понятие.
Выбрать методы, с помощью которых
предполагается выполнение открытого задания
учеником. Определить форму конечного
продукта;
Сформулировать задание в доступной для
учеников форме.

22. Этапы становления ИТД

Ориентировки
Поиска
Преобразования
Интеграции

23.

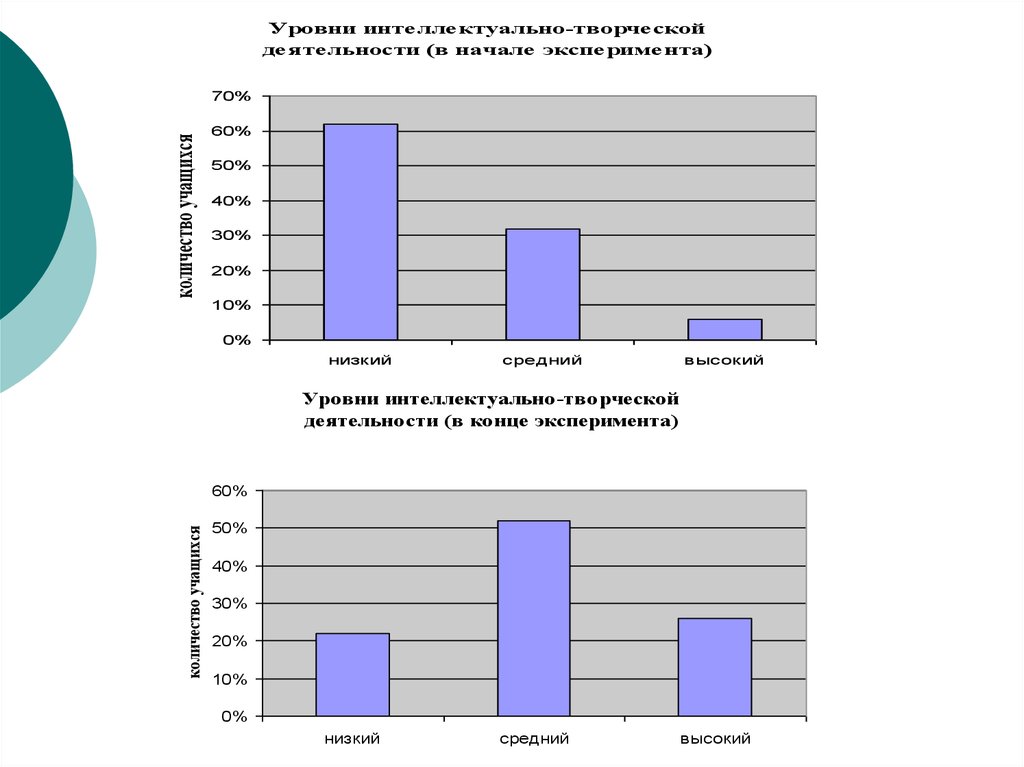
Уровни интеллектуально-творческой
деятельности (в начале эксперимента)
количество учащихся
70%
60%
50%
40%
30%
20%
10%
0%
низкий
средний
высокий
Уровни интеллектуально-творческой
деятельности (в конце эксперимента)
количество учащихся
60%
50%
40%
30%
20%
10%
0%
низкий
средний
высокий

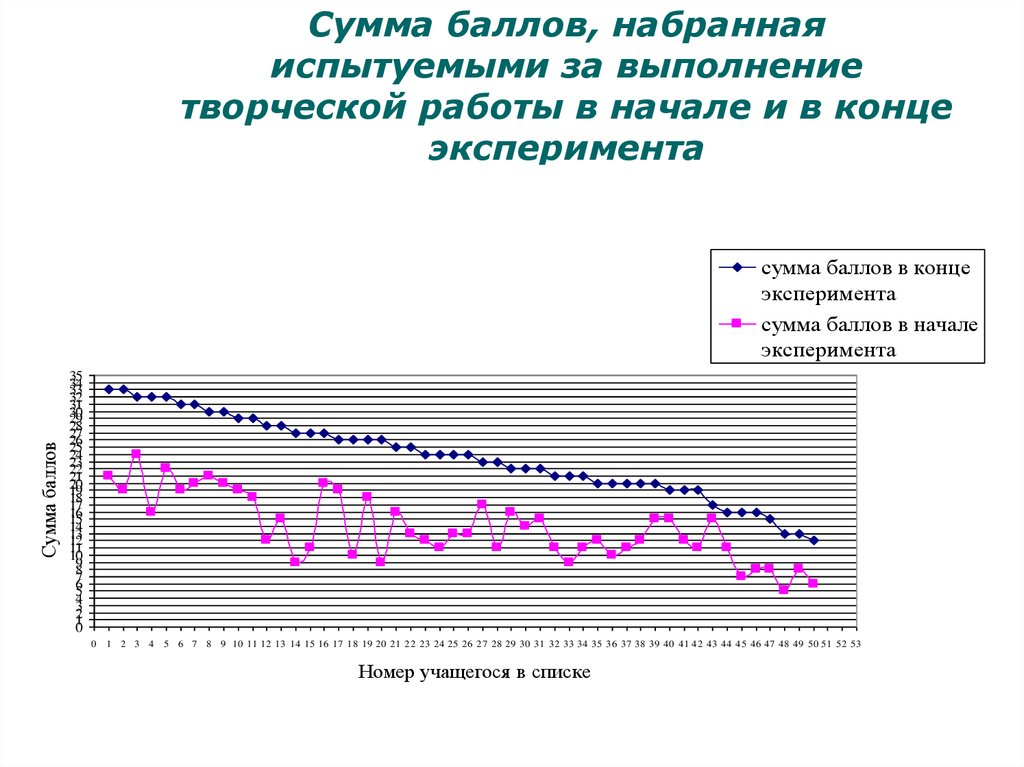
24. Сумма баллов, набранная испытуемыми за выполнение творческой работы в начале и в конце эксперимента

Сумма баллов
сумма баллов в конце
эксперимента
сумма баллов в начале
эксперимента
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
Номер учащегося в списке

25. Спасибо за внимание!