Правильные многогранники. Построить треугольник DCE

1.

Правильные многогранники

2.

Проверка домашнего задания
№1. Построить треугольник DCE, в
котором DC= 6см 8мм, CE=3cм 5 мм,
C = 65°.

3.

Всегда
ли можно
построить такой
треугольник?

4.

Проверка домашнего задания
№2. Построить треугольник MNK, в
котором MN = 4см 5мм, M = 38°,
N=99°.

5.

Всегда
ли можно
построить такой
треугольник?

6.

Проверка домашнего задания
№3. Построить треугольник ABC, в
котором AB = 4см 5мм, BC= 5cм 6мм,
AC=6см.

7.

Всегда
ли можно
построить такой
треугольник?

8.

Эпиграф к уроку:
Одна из заповедей Пифагора:
« Не делай никогда того, чего не
знаешь, но научись всему, что
следует знать».

9.

Загадка
Со времен Пифагора известны они
В них равные стороны, равны углы.
Их встретим в орнаментах и на
паркетах,
В стихотворениях разных поэтов,
И даже пчелы с ними работают,
строя в их форме домики-соты.

10.

Письмо
Однажды обыкновенный
мальчик Джеймс,
увлекшись изготовлением
моделей многогранников,
написал в письме к отцу: «…
я сделал тетраэдр,
додекаэдр и еще два эдра,
для которых не знаю
правильного названия». Эти
слова знаменовали
рождение, в пока ничем не
примечательном мальчике
великого физика Джеймса
Кларка Максвелла.

11.

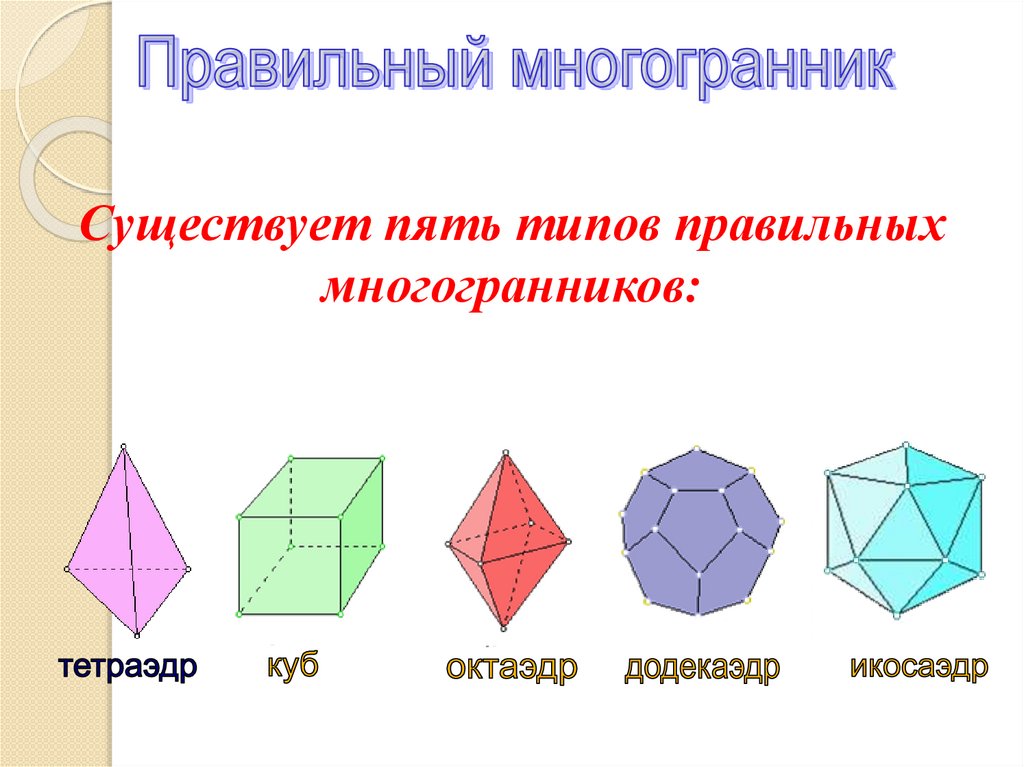
Многогранник называется
правильным, если его поверхность
составлена из правильных
многоугольников.

12.

Существует пять типов правильных
многогранников:

13.

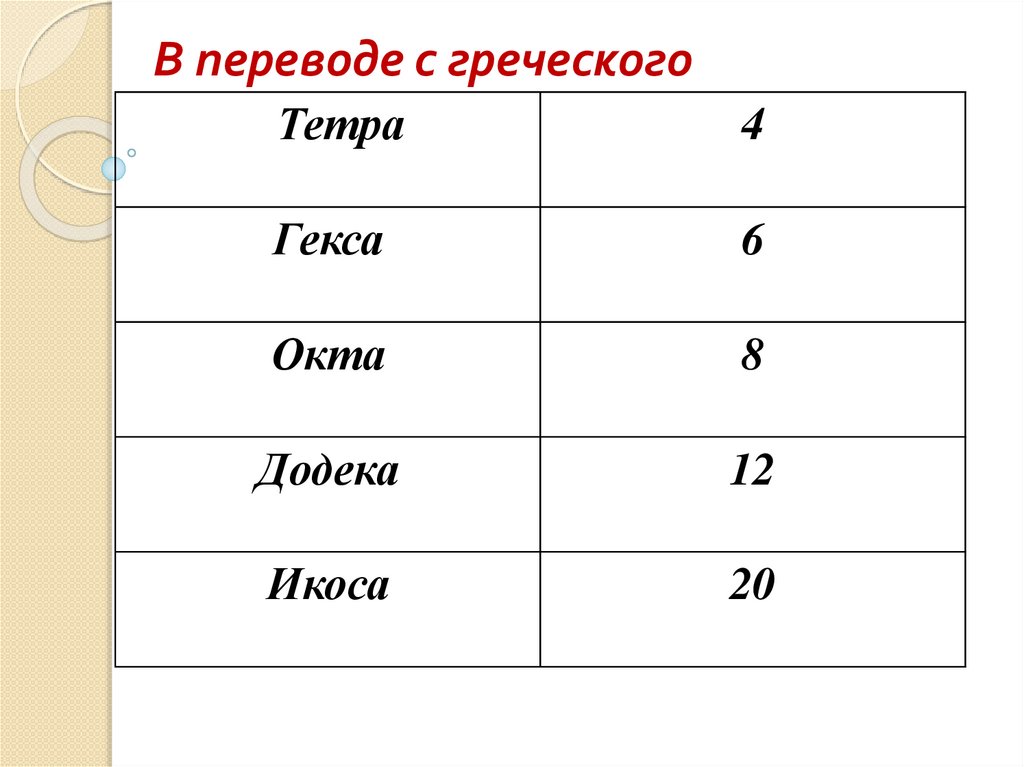
В переводе с греческого
Тетра
4
Гекса
6
Окта
8
Додека
12
Икоса
20

14.

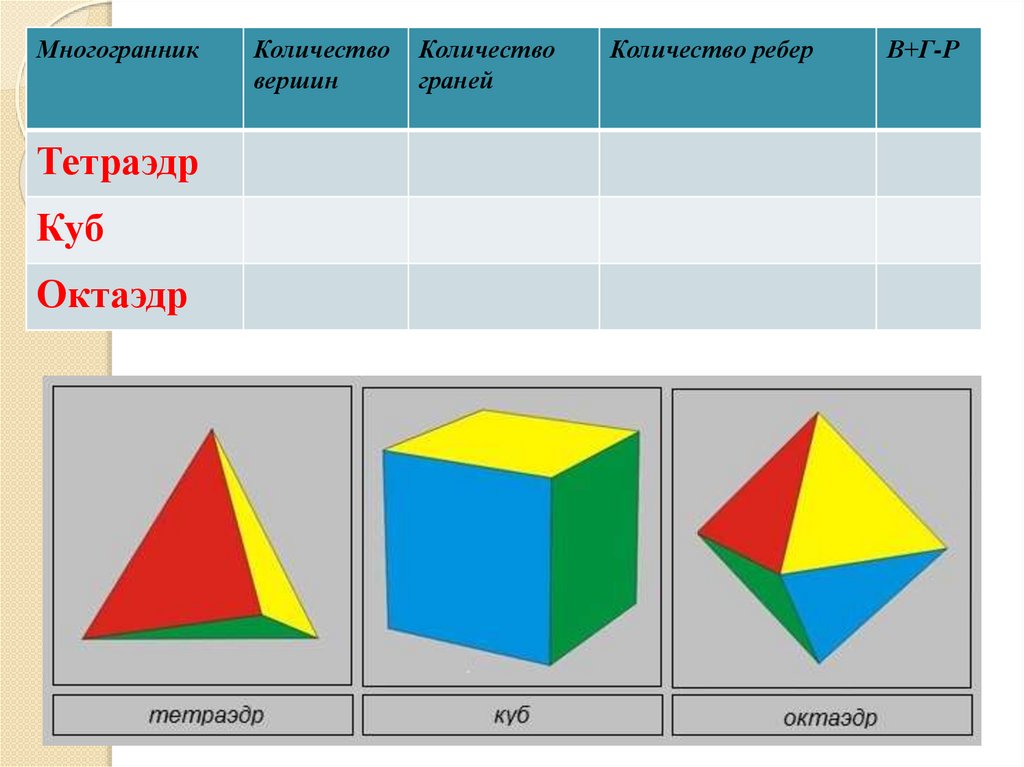
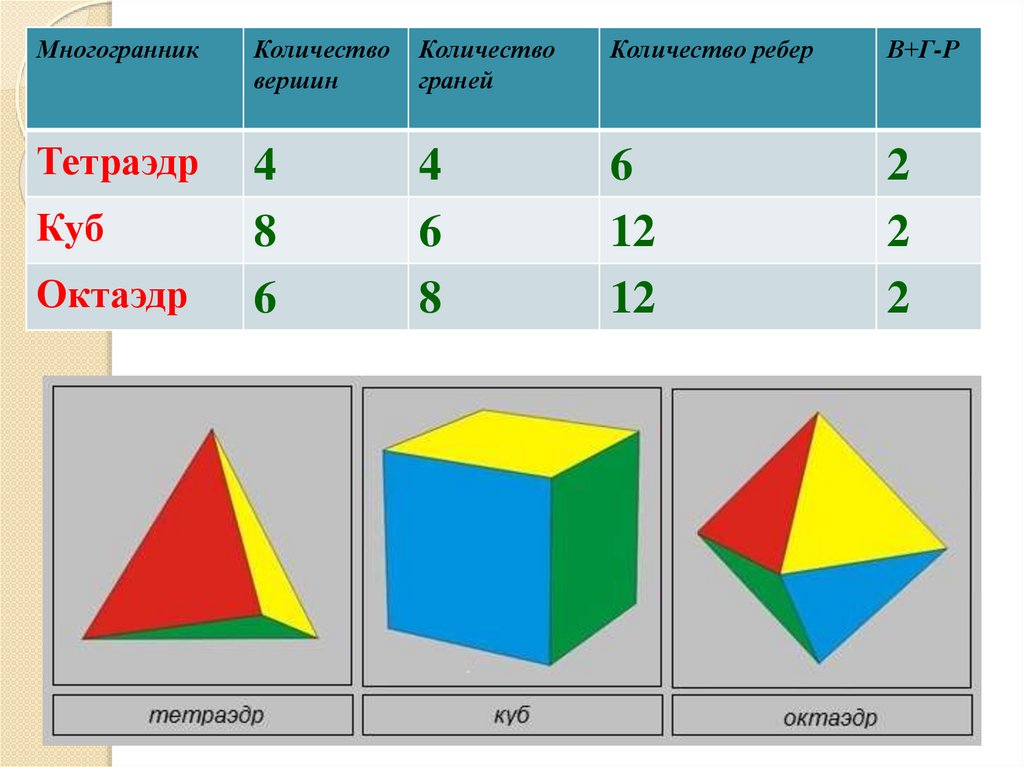
Многогранник
Тетраэдр
Куб
Октаэдр
Количество
вершин
Количество
граней
Количество ребер
В+Г-Р

15.

Многогранник
Количество
вершин
Количество
граней
Количество ребер
В+Г-Р
Тетраэдр
4
8
6
4
6
8
6
12
12
2
2
2
Куб
Октаэдр

16.

Теорема Эйлера.
Пусть В - число вершин выпуклого
многогранника, Р - число его рёбер и Г число граней. Тогда верно равенство
В+Г-Р=2.
Число X = В+Г-Р называется эйлеровой
характеристикой многогранника. Согласно
теореме Эйлера, для выпуклого
многогранника эта характеристика равна
2.

17.

Леонард Эйлер
(1707 – 1783 гг.)
немецкий математик и физик
Эйлер родился в швейцарском городе Базеле в 1707 году. Но почти
всюжизнь прожил в России.
Начальное обучение будущий ученый прошел дома под
руководством отца, учившегося некогда математике у
Якоба Бернулли. В 13 лет Эйлер поступил на факультет
искусств Базельского университета.
Среди других предметов на этом факультете изучались
элементарная математика и астрономия, которые преподавал Иоганн Бернулли. Вскоре Бернулли заметил талант
юного слушателя и начал заниматься с ним отдельно. Так
как в то время не существовало учебников по математике, вместе
разбирать
прочитанное. «Несомненно, это лучший способ делать успехи в
математических науках, – писал Эйлер впоследствии. После
разъяснения одной трудности
десятки других исчезали »

18.

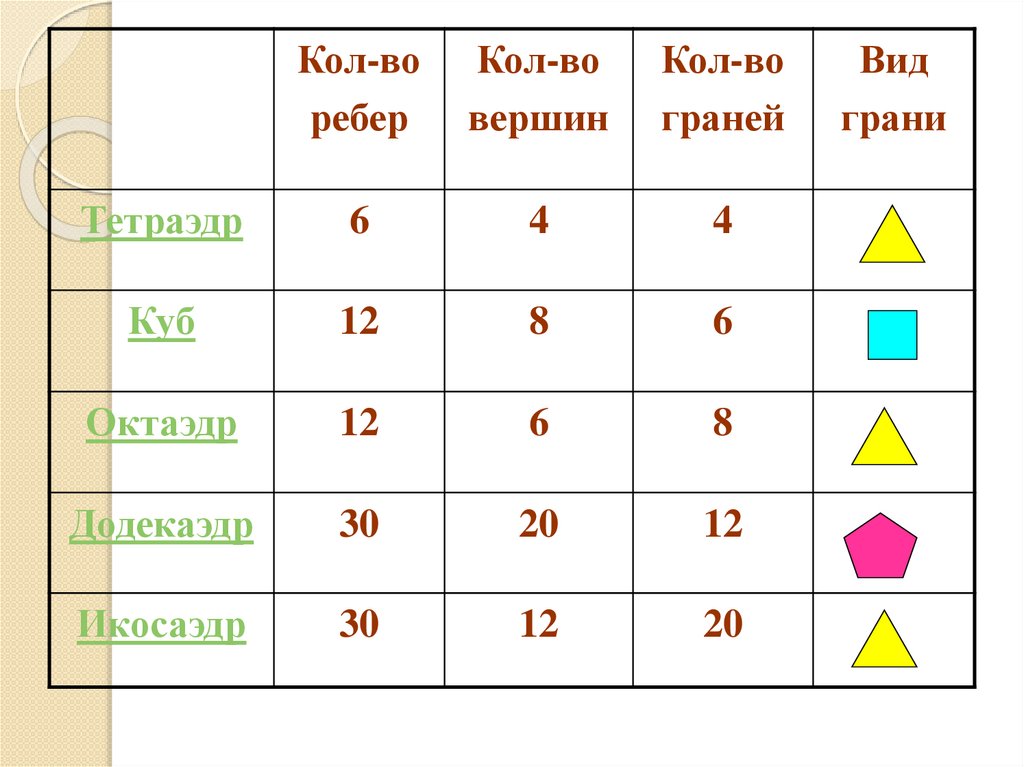
Кол-во
ребер
Кол-во
вершин
Кол-во
граней
Тетраэдр
6
4
4
Куб
12
8
6
Октаэдр
12
6
8
Додекаэдр
30
20
12
Икосаэдр
30
12
20
Вид
грани

19.

D
Составлен из
четырёх
равносторонних
треугольников.
Каждая его
вершина является
вершиной трёх
треугольников.

20.

21.

Составлен из
восьми
равносторонних
треугольников.
Каждая вершина
октаэдра
является
вершиной
четырёх
треугольников.

22.

Составлен из
двенадцати правильных
пятиугольников. Каждая
вершина додекаэдра
является вершиной трёх
правильных
пятиугольников.

23.

24.

25.

26.

Развертки многогранников

27.

1 вариант. Выполнить задание
в рамке стр.36
2 вариант .Выполнить задание
в рамке стр.37